
Энергетические характеристики двухполюсников
Содержание:
Энергетические характеристики двухполюсников:
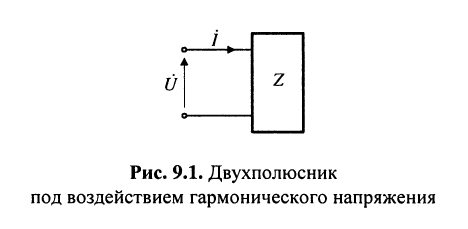
Всякую пассивную электрическую цепь, находящуюся под воздействием источника гармонического напряжения, можно рассматривать как двухполюсник (рис. 9.1), обладающий, в общем случае, комплексным (7.26) сопротивлением 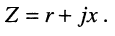
Средняя мощность  , потребляемая таким двухполюсником в режиме гармонических колебаний, находится в соответствии с (7.15) и (7.18) по формуле
, потребляемая таким двухполюсником в режиме гармонических колебаний, находится в соответствии с (7.15) и (7.18) по формуле
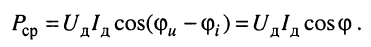 (9.1)
(9.1)
Согласно закону Ома действующие значения напряжения 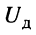 и тока
и тока 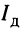 связаны зависимостью:
связаны зависимостью:
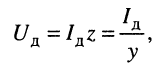
где 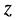 и
и 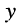 представляют собой полное сопротивление и полную проводимость двухполюсника соответственно (см. лекцию 7). Поэтому формула (9.1) может быть представлена в виде:
представляют собой полное сопротивление и полную проводимость двухполюсника соответственно (см. лекцию 7). Поэтому формула (9.1) может быть представлена в виде:
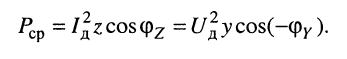 (9.2)
(9.2)
Поскольку, с учётом чётности функции косинуса, величины
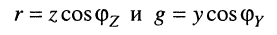
являются активными составляющими сопротивления и проводимости двухполюсника, выражение (9.2) принимает вид:
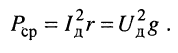 (9.3)
(9.3)
Таким образом, средняя за период мощность равна мощности, рассеиваемой на резистивном сопротивлении (проводимости) двухполюсника. По этой причине мощность 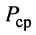 также называется активной и измеряется в ваттах (Вт).
также называется активной и измеряется в ваттах (Вт).
Формулу (9.1) можно переписать в виде:
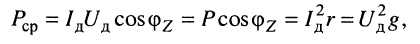
где произведение действующих значений напряжения и тока
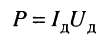 (9.4)
(9.4)
называют полной (кажущейся) мощностью.
Комплексную мощность Р найдём по действующей комплексной амплитуде напряжения
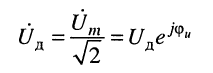
на зажимах двухполюсника и действующей комплексной амплитуде тока
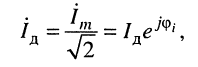
проходящего через двухполюсник. При таких обозначениях квадрат действующего значения тока можно записать как произведение действующей комплексной амплитуды тока на её сопряжённую величину:
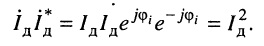
Тогда из (9.3) имеем:
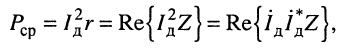
но согласно закону Ома
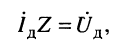
поэтому получаем:
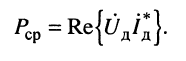 (9.5)
(9.5)
Последнее выражение означает, что средняя мощность, потребляемая двухполюсником, равна вещественной части произведения действующей комплексной амплитуды напряжения на его входе и комплексной величины, сопряжённой с действующей комплексной амплитудой тока, проходящего через входные зажимы двухполюсника.
Формула (9.5) даёт основание записать выражение для комплексной мощности:
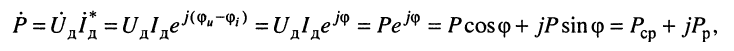 (9.6)
(9.6)
вещественная часть которой представляет собой среднюю мощность, потребляемую двухполюсником, мнимая часть  —реактивную мощность:
—реактивную мощность:
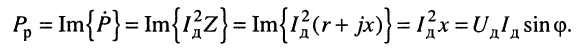 (9.7)
(9.7)
Выводы:
- полная мощность
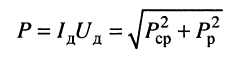 (9.8)
(9.8)
есть произведение действующих значений тока и напряжения, измеряется в вольт-амперах 
- средняя мощность
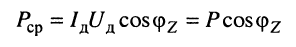
представляет собой полную мощность, умноженную на коэффициент мощности  измеряется в ваттах (Вт). Средняя (активная) мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию!), поэтому
измеряется в ваттах (Вт). Средняя (активная) мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию!), поэтому 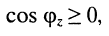 т. е. для пассивного двухполюсника всегда имеет место неравенство
т. е. для пассивного двухполюсника всегда имеет место неравенство 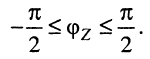 Случай Р = 0, когда
Случай Р = 0, когда 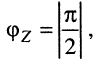 двухполюсника, который не имеет активных сопротивлении, но содержит только индуктивные и ёмкостные элементы;
двухполюсника, который не имеет активных сопротивлении, но содержит только индуктивные и ёмкостные элементы;
- коэффициент мощности (косинус фи)
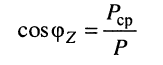 (9.9)
(9.9)
равен отношению средней мощности к полной мощности, потребляемой двухполюсником, и представляет собой косинус угла сдвига фаз между напряжением и током; 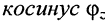 является важной характеристикой электрических машин и линий передач переменного тока, отражая потери энергии: чем больше
является важной характеристикой электрических машин и линий передач переменного тока, отражая потери энергии: чем больше 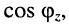 тем меньше потери при передаче энергии по линии и выше КПД электрических машин; при
тем меньше потери при передаче энергии по линии и выше КПД электрических машин; при 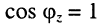 имеем
имеем 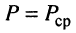 и
и 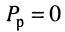 , т. е. цепь носит чисто активный характер, и сдвиг фаз между
, т. е. цепь носит чисто активный характер, и сдвиг фаз между 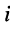 током и напряжением и равен нулю;
током и напряжением и равен нулю;
- реактивная мощность
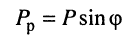
равна произведению полной мощности на синус угла сдвига фаз между напряжением и током; она не связана с выделением энергии в элементе, поэтому измеряется в вольт-амперах реактивных (ВАр); реактивная мощность отражает процесс обмена энергией между цепью и источником. В зависимости от знака 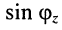 реактивная мощность может быть положительной или отрицательной: при
реактивная мощность может быть положительной или отрицательной: при 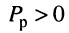 энергия запасается в магнитном поле цепи (индуктивностях), при
энергия запасается в магнитном поле цепи (индуктивностях), при 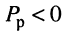 энергия запасается в электрическом поле (ёмкостях). Реактивная мощность отражает дополнительные потери в системах передачи энергии, поэтому всегда стремятся достичь её минимально возможной величины за счёт компенсации реактивных составляющих полного сопротивления таких систем;
энергия запасается в электрическом поле (ёмкостях). Реактивная мощность отражает дополнительные потери в системах передачи энергии, поэтому всегда стремятся достичь её минимально возможной величины за счёт компенсации реактивных составляющих полного сопротивления таких систем;
- комплексная мощность есть число, модуль которой равен полной мощности.
Пример 9.1.
К источнику с напряжением
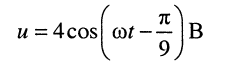
подключена нагрузка, ток в которой
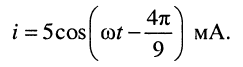
Определить: активную (среднюю), полную и реактивную мощности, а также характер реактивного сопротивления.
Решение. Прежде всего найдём действующие амплитуды напряжения и тока:
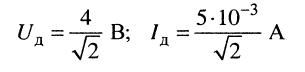
и разность фаз между напряжением и током:
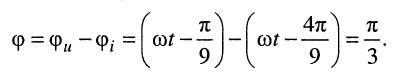
По формуле (9.1) вычислим активную мощность:
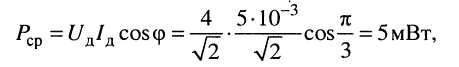
по формуле (9.4) найдём полную мощность:
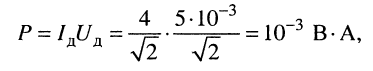
а по формуле (9.7) — реактивную мощность:
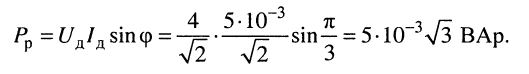
Поскольку реактивная мощность положительна, то реактивное сопротивление является индуктивным.
Максимум средней мощности в нагрузке
Условия баланса мощностей:
Поскольку комплексные напряжения и комплексные токи в ветвях цепи удовлетворяют законам Кирхгофа, то можно показать (теорема Теллегена), что сумма мощностей всех ветвей схемы равна нулю:
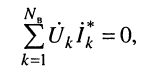 (9.10)
(9.10)
где 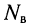 — количество ветвей в схеме. Но это возможно только при равенстве нулю вещественной и мнимой составляющих:
— количество ветвей в схеме. Но это возможно только при равенстве нулю вещественной и мнимой составляющих:
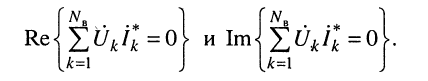 (9.11)
(9.11)
Полученные соотношения называют условиями баланса мощностей комплексной, активной и реактивной соответственно. Их используют для проверки решений задач анализа цепей символическим методом в режиме гармонических колебаний.
Условия максимума средней мощности в нагрузке
Задача 9.1.
Имеется генератор гармонических колебаний (рис. 9.2) с ЭДС 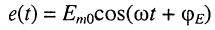 и внутренним сопротивлением
и внутренним сопротивлением 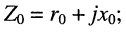 требуется определить сопротивление нагрузки
требуется определить сопротивление нагрузки 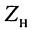 , на котором выделяется максимум средней мощности, и величину этой мощности
, на котором выделяется максимум средней мощности, и величину этой мощности 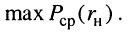
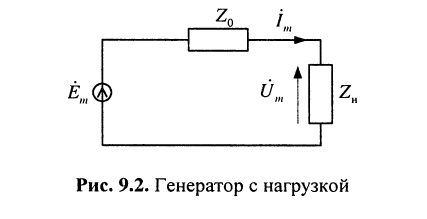
Решение. Задачу удобно решать в терминах комплексных амплитуд. Запишем комплексную амплитуду ЭДС генератора
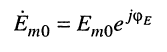
и комплексное сопротивление нагрузки
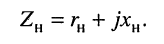
Тогда комплексная амплитуда тока в цепи определится по закону Ома
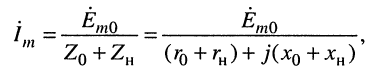
а комплексная амплитуда напряжения на нагрузке найдётся из выражен
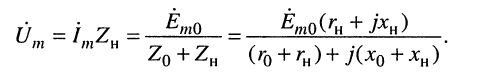 (9.12)
(9.12)
Следовательно, комплексная мощность (9.6), развиваемая на нагрузке, такова:
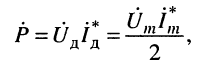 (9.13)
(9.13)
где комплексно-сопряжённая амплитуда тока:
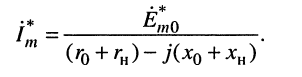 (9.14)
(9.14)
Соотношения (9.12)—(9.14) позволяют найти комплексную мощность в нагрузке:
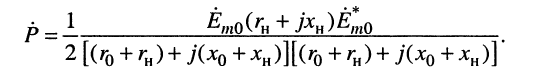 (9.15)
(9.15)
Поскольку произведения комплексно-сопряжённых величин равны квадратам модулей сомножителей:
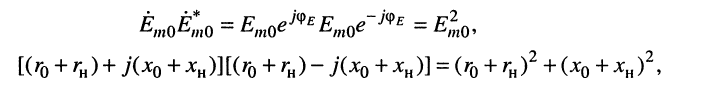
выражение (9.15) получает вид:
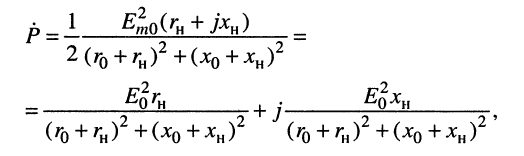 (9.16)
(9.16)
где 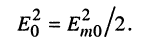
Вещественная часть комплексной мощности (9.16) согласно (9.5) является средней мощностью, поэтому
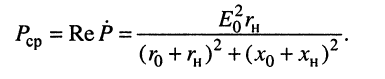 (9.17)
(9.17)
Из (9.17) найдём искомые условия, при которых средняя мощность, выделяемая в нагрузке, является максимальной.
Первое условие. Максимум средней мощности, выделяемой в нагрузке, будет достигнут, если 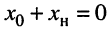 , т. е. когда
, т. е. когда
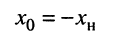 (9.18)
(9.18)
реактивные составляющие внутреннего сопротивления генератора и нагрузки компенсируют друг друга.
Поэтому из первого условия (9.18) имеем:
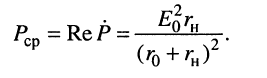 (9.19)
(9.19)
Далее выясним, при каком соотношении активных составляющих 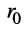 и
и 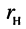 внутреннего сопротивления генератора и сопротивления нагрузки соответственно будет достигаться максимум средней мощности, для чего найдём максимум функции
внутреннего сопротивления генератора и сопротивления нагрузки соответственно будет достигаться максимум средней мощности, для чего найдём максимум функции 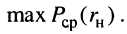 Это соотношение и составит второе условие максимума средней мощности.
Это соотношение и составит второе условие максимума средней мощности.
Поскольку  определено свойствами генератора, для нахождения максимума функции найдём её производную по переменной
определено свойствами генератора, для нахождения максимума функции найдём её производную по переменной  :
:
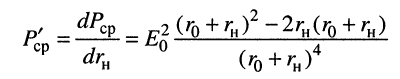
и приравняем производную нулю
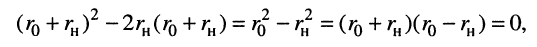 откуда получаем второе условие.
откуда получаем второе условие.
Второе условие. Максимум средней мощности  выделяемой
выделяемой
в нагрузке, достигается при равенстве активных составляющих внутреннего сопротивления генератора и сопротивления нагрузки:
 (9.20)
(9.20)
Условия (9.18) и (9.20) можно объединить, если записать равенство комплексного сопротивления нагрузки комплексно-сопряжённому внутреннему сопротивлению генератора
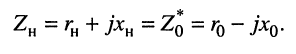 (9.21)
(9.21)
Выводы:
- генератор гармонических колебаний развивает в нагрузке максимальную среднюю мощность, если сопротивление нагрузки сопряжено с внутренним сопротивлением генератора;
- максимально возможная средняя мощность, которую может развить генератор в нагрузке, равна:
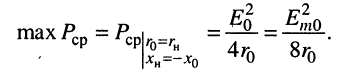 (9.22)
(9.22)
Коэффициент полезного действия генератора. Согласованная нагрузка
Определение
Коэффициентом полезного действия генератора (КПД) 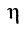 называется отношение средней (активной) мощности
называется отношение средней (активной) мощности 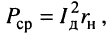 потребляемой нагрузкой, к суммарной средней (активной) мощности
потребляемой нагрузкой, к суммарной средней (активной) мощности 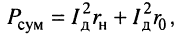 потребляемой всей цепью:
потребляемой всей цепью:
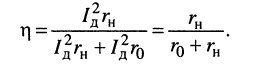 (9.23)
(9.23)
Из определения (9.23) следует (рис. 9.3):
1. КПД генератора при сопряжённой нагрузке, когда достигается максимум средней мощности, равен 0,5; это объясняется тем, что на внутреннем сопротивлении генератора рассеивается та же средняя мощность, что и в нагрузке.
2. С ростом 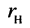 КПД увеличивается, хотя средняя мощность в нагрузке падает, причём с ростом отношения
КПД увеличивается, хотя средняя мощность в нагрузке падает, причём с ростом отношения 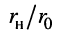 КПД монотонно возрастает и при
КПД монотонно возрастает и при 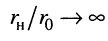 приближается к
приближается к 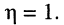
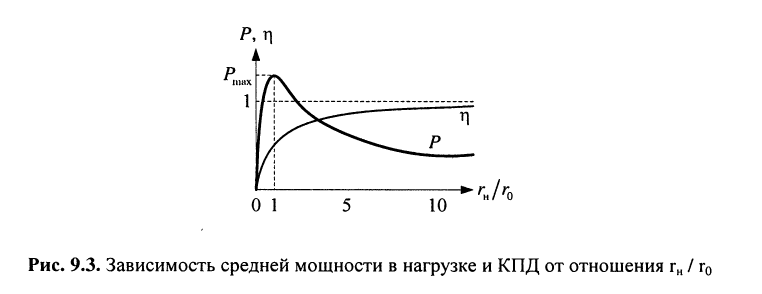
В энергетических системах, где важно получение высокого КПД, стремятся к тому, чтобы 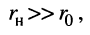 но в этом случае значительное снижение сопротивления нагрузки приводит к опасному повышению мощности, расходуемой в генераторе, что может привести к аварийному исходу.
но в этом случае значительное снижение сопротивления нагрузки приводит к опасному повышению мощности, расходуемой в генераторе, что может привести к аварийному исходу.
В системах связи часто сопротивление нагрузки выбирают равным внутреннему сопротивлению генератора:
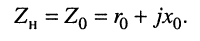
В таком случае говорят, что генератор нагружен согласованно, а сопротивление нагрузки называют согласованным.
Важно:
напряжение на согласованной нагрузке независимо от частоты всегда равно половине задающего напряжения генератора, и средняя мощность, выделяемая в согласованной нагрузке, равна:
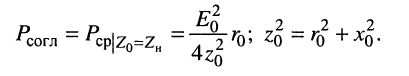
Мощность 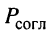 меньше средней мощности в сопряжённой нагрузке, поскольку
меньше средней мощности в сопряжённой нагрузке, поскольку
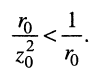
Это объясняется тем, что при согласованной нагрузке реактивные составляющие внутреннего сопротивления генератора и сопротивления нагрузки суммируются, а при сопряжённой — они компенсируют друг друга, последнее ведёт к увеличению как амплитуды тока в нагрузке, так и амплитуды напряжения на ней.
Замечание:
В дальнейшем будет показано, что при согласованной нагрузке сохраняются соотношения между амплитудами и фазами частотных составляющих сигнала, т. е. сохраняется форма сигнала.
Пример 9.2.
Найти сопротивление нагрузки 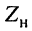 (рис. 9.4), при котором в этой нагрузке достигался бы максимум средней мощности, и рассчитать величину этой мощности.
(рис. 9.4), при котором в этой нагрузке достигался бы максимум средней мощности, и рассчитать величину этой мощности.
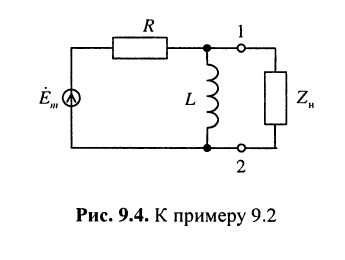
Решение. При решении этой задачи воспользуемся условиями максимума
средней мощности в нагрузке и теоремой об эквивалентном генераторе.
1. Максимум средней мощности будет достигаться, если согласно (9.21) внутреннее сопротивление 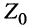 эквивалентного генератора, которым можно заменить всю цепь, действующую на нагрузку, будет удовлетворять равенству:
эквивалентного генератора, которым можно заменить всю цепь, действующую на нагрузку, будет удовлетворять равенству:
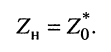
2. По теореме об эквивалентном генераторе находим:
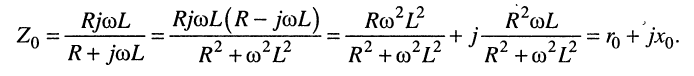
Комплексное сопротивление 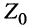 имеет индуктивный характер, поскольку реактивная составляющая этого сопротивления положительна
имеет индуктивный характер, поскольку реактивная составляющая этого сопротивления положительна 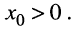 По этой причине комплексное сопротивление нагрузки должно иметь ёмкостной характер:
По этой причине комплексное сопротивление нагрузки должно иметь ёмкостной характер:
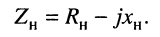
3. Представим нагрузку в виде двухполюсника из последовательно соединённых активного сопротивления и ёмкости:
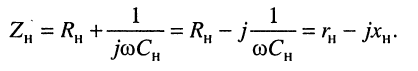
4. Приравняем вещественные 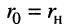 и мнимые
и мнимые 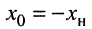 части сопротивлений
части сопротивлений 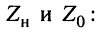
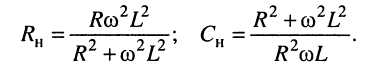
5. Найдём напряжение холостого хода на зажимах 1-2, создаваемое эквивалентным генератором:
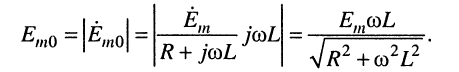
6. По формуле (9.22) находим максимальную среднюю мощность, которую может развить генератор в нагрузке:
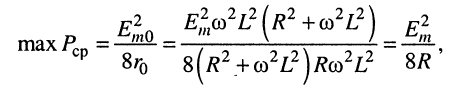
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Гармонические напряжения и токи