Элементы теории ошибок - определение и вычисление с примерами решения

Содержание:

Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (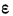

Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.

Различают два вида ошибок измерения:

1. систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
2. случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.

Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.

Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.

Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.

В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.

Средняя ошибка сводного результата измерения

Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:

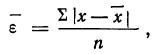
где n — число измерений, х — численное значение отдельных измерений, 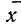— средняя арифметическая из результатов измерений.

За меру точности соответствия принятой средней арифметической 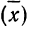истинному значению измеряемой величины (A) принимают среднюю ошибку сводного результата измерения, вычисляемую по формуле:

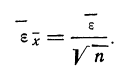
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.

Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:

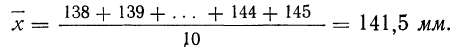
Найдем ошибки измерения:

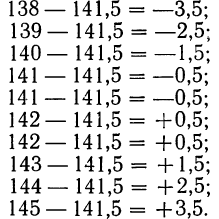
Следовательно:

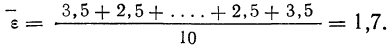
Теперь можно вычислить среднюю ошибку сводного результата измерения:

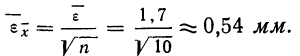
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.

Средняя квадратическая ошибка

Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.

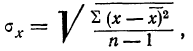
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:

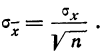
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 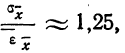 если случайные ошибки подчиняются Гауссову закону нормального распределения.

Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:

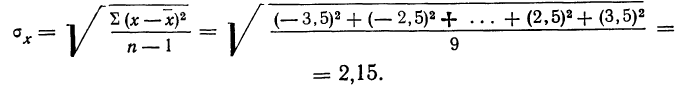
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:

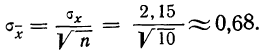
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:

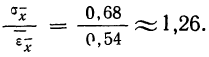
Вероятная ошибка

За меру точности одного измерения иногда принимают вероятную ошибку:

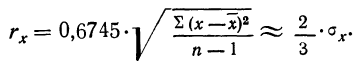
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:

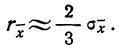
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:

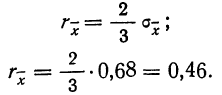
Наиболее вероятные границы сводных результатов измерения

Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 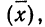называемых в теории ошибок «кажущимися ошибками» 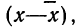позволяет произвести оценку точности соответствия средней арифметической неизвестному истинному значению измеряемой величины (A).

Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:

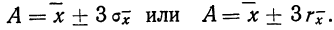
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).

Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 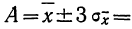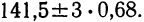Значит, истинное значение размера детали находится в границах от 141,5—2,04 до 141,5+2,04.