
Элементы матричного анализа с примерами решения
Содержание:
Векторы на плоскости и в пространстве:
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Вектором называется направленный отрезок 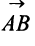
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
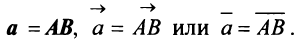
Длиной (или модулем) 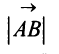 вектора
вектора 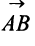 называется число, равное длине отрезка
называется число, равное длине отрезка 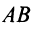 , изображающего вектор.
, изображающего вектор.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 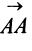 , то такой вектор называют нулевым и обозначают
, то такой вектор называют нулевым и обозначают 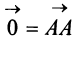 . Длина нулевого вектора равна нулю:
. Длина нулевого вектора равна нулю: 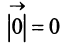 . Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
Произведением вектора 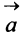 на число
на число 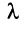 называется вектор
называется вектор 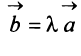 , имеющий длину
, имеющий длину 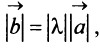 направление которого совпадает с направлением вектора
направление которого совпадает с направлением вектора 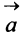 , если
, если 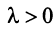 , и противоположно ему, если
, и противоположно ему, если 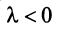 (рис. 3.2).
(рис. 3.2).
Противоположным вектором 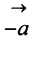 называется произведение вектора
называется произведение вектора 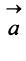 на число
на число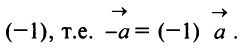
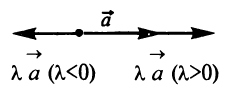
Рис. 32
Суммой двух векторов  и
и  называется вектор
называется вектор 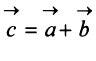 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец с концом вектора
, а конец с концом вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (рис. 3.3) (правило треугольника).
(рис. 3.3) (правило треугольника). 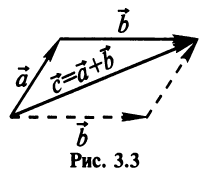
Очевидно, что вектор 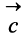 в этом случае представляет диагональ параллелограмма, построенного на векторах
в этом случае представляет диагональ параллелограмма, построенного на векторах  и
и  (рис. 3.3) (правило параллелограмма).
(рис. 3.3) (правило параллелограмма).
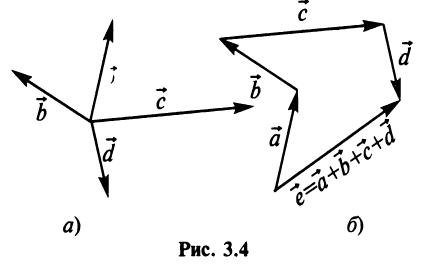
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 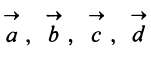 (рис. 3.4а) есть вектор
(рис. 3.4а) есть вектор 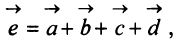 начало которого совпадает с началом вектора
начало которого совпадает с началом вектора  , а конец — с концом вектора
, а конец — с концом вектора 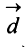 (правило многоугольника) (рис. 3.4 б).
(правило многоугольника) (рис. 3.4 б).
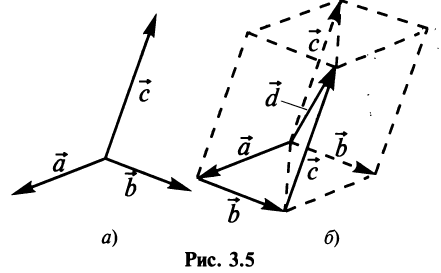
Нетрудно убедиться. что вектор 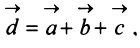 определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах
определяемый таким образом, представляет диагональ параллелепипеда, построенного на векторах  ,
, и
и 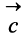 , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда) (рис. 3.5).
Разностью двух векторов  и
и  называется сумма вектора
называется сумма вектора  и вектора
и вектора 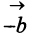 , противоположного
, противоположного  (рис. 3.6).
(рис. 3.6).
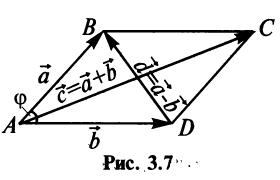
Легко убедиться в том, что в параллелограмме, построенном на векторах 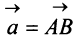 и
и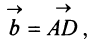 одна диагональ — вектор —представляет сумму векторов
одна диагональ — вектор —представляет сумму векторов  и
и  , а другая диагональ — вектор
, а другая диагональ — вектор 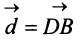 — их разность (рис. 3.7).
— их разность (рис. 3.7).
Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора
параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора  называются координаты его конечной точки. Так, вектор
называются координаты его конечной точки. Так, вектор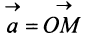 на плоскости
на плоскости 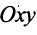 являются два числа
являются два числа 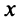 и
и 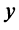 (
( 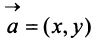 — рис. 3.8.), а в пространстве
— рис. 3.8.), а в пространстве 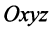 — три числа
— три числа 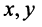 и
и 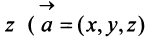 — рис. 3.9).
— рис. 3.9).
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов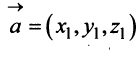 и
и 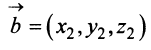 являются соответственно векторы
являются соответственно векторы
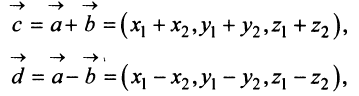 ,
,
а произведение вектора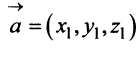 на число
на число 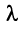 есть вектор
есть вектор 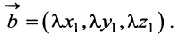 На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
На рис. 3.8 и 3.9 видно, что длина вектора равна корню квадратному из суммы квадратов его координат:
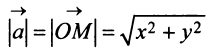 или
или
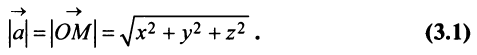
Определение. Скалярным произведением 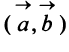 двух векторов
двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 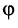 между ними:
между ними:
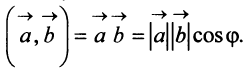
Выразим скалярное произведение через координаты векторов  и
и  .
.
Из треугольника  (рис. 3.7), сторонами которого являются векторы
(рис. 3.7), сторонами которого являются векторы 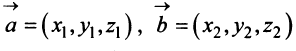 и
и 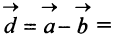
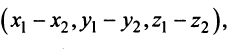 по теореме косинусов следует, что
по теореме косинусов следует, что
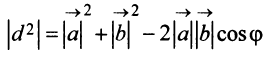 , откуда
, откуда 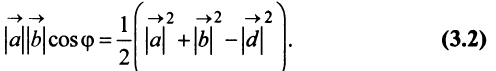
Учитывая формулу длины вектора (3.1) найдем
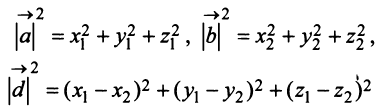 и после преобразования выражения (3.2) получим
и после преобразования выражения (3.2) получим
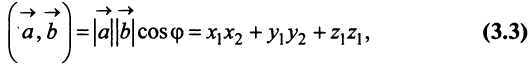
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 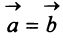 угол
угол 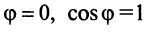 и
и
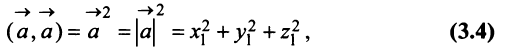
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 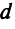 между двумя точками плоскости
между двумя точками плоскости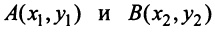 можно рассматривать как длину вектора
можно рассматривать как длину вектора 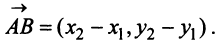
Поэтому 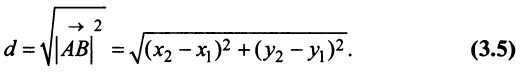
Угол между векторами и
и  определяется по формуле
определяется по формуле
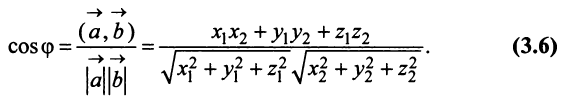
Пример:
Даны векторы 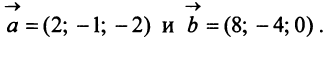
Найти: а)векторы 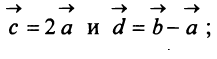 б)длины векторов
б)длины векторов 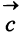 и
и 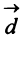 ; в) скалярный квадрат вектора
; в) скалярный квадрат вектора 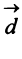 ; г) скалярное произведение векторов
; г) скалярное произведение векторов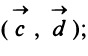 д)угол между векторами
д)угол между векторами 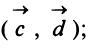
Решение:
а) По определению 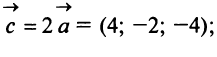
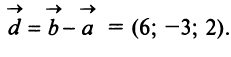
б) По формуле (3.1) найдем длины векторов 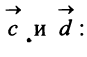
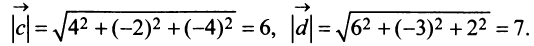
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.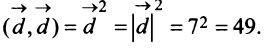
г) По формуле (3.3) скалярное произведение
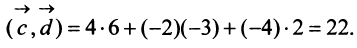
д) По формуле (3.6) угол между векторами 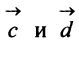 определяется равенством:
определяется равенством:
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение. -мерным вектором называется упорядоченная совокупность
-мерным вектором называется упорядоченная совокупность 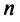 действительных чисел, записываемых в виде
действительных чисел, записываемых в виде 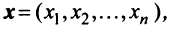 где
где 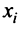 —
— 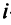 -я компонента вектора
-я компонента вектора 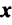 .
.
Понятие  -мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором
-мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором 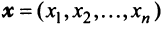 , а соответствующие цены — вектором
, а соответствующие цены — вектором 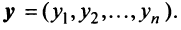
Два  -мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.
-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. 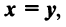 если
если 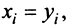
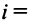
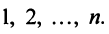
Суммой двух векторов одинаковой размерности п называется вектор 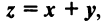 компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.
компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. 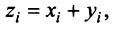
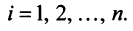
Произведением вектора  на действительное число
на действительное число 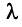 называется вектор
называется вектор 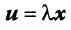 , компоненты
, компоненты 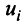 которого равны произведению
которого равны произведению 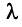 на соответствующие компоненты вектора
на соответствующие компоненты вектора  , т.е.
, т.е. 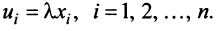
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
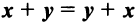 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: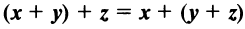 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы; — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;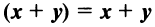 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;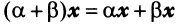 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;- Существует нулевой вектор
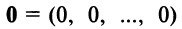 такой, что
такой, что 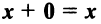 для любого вектора
для любого вектора  (особая роль нулевого вектора);
(особая роль нулевого вектора); - Для любого вектора
 существует противоположный вектор
существует противоположный вектор 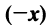 такой, что
такой, что 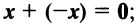
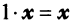 для любого вектора
для любого вектора  (особая роль числового множителя 1).
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под 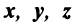 можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 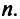 Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу
Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу  , не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже
, не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже  . А множество многочленов степени не выше
. А множество многочленов степени не выше  , но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
, но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора  на действительное число 0 и существование для каждого вектора
на действительное число 0 и существование для каждого вектора 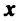 единственного противоположного вектора (—
единственного противоположного вектора (—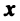 ), равного произведению этого вектора на действительное число (- 1).
), равного произведению этого вектора на действительное число (- 1).
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 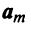 называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства
векторного пространства 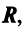 если он равен сумме произведений этих векторов на произвольные действительные числа:
если он равен сумме произведений этих векторов на произвольные действительные числа:
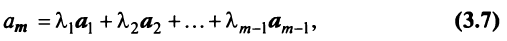
где 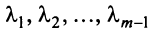 — какие угодно действительные числа.
— какие угодно действительные числа.
Определение. Векторы  векторного пространства
векторного пространства 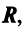 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 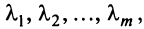 не равные одновременно нулю, что
не равные одновременно нулю, что
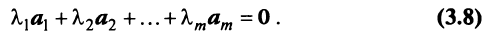
В противном случае векторы  называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы  линейно независимы, если равенство (3.8) справедливо лишь при
линейно независимы, если равенство (3.8) справедливо лишь при 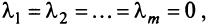 и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 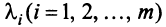 отлично от нуля.
отлично от нуля.
Можно показать (аналогично § 1.6), что если векторы  линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 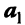 и
и 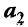 на плоскости. Действительно, условие (3.8)
на плоскости. Действительно, условие (3.8) 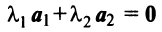 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 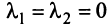 , ибо если, например,
, ибо если, например, 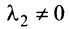 , то
, то 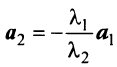 , и векторы
, и векторы 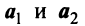 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
 имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например, 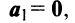 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 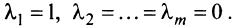
- Если часть векторов
 являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы 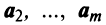 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 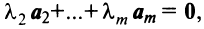 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 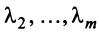 и
и 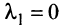 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы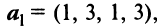
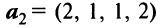 и
и 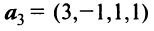 линейно зависимыми.
линейно зависимыми.
Решение:
Составим векторное равенство 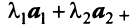
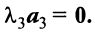 Записывая
Записывая 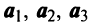 в виде вектор-столбцов, получим
в виде вектор-столбцов, получим 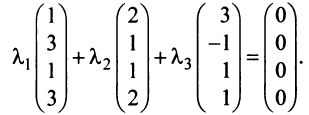
Задача свелась таким образом к решению системы:
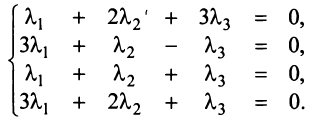
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
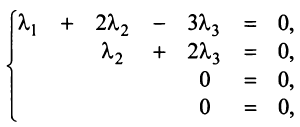
откуда найдем, бесконечное множество ее решений 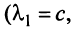
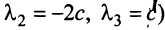 , где с — произвольное действительное число.
, где с — произвольное действительное число.
Итак, для 'данных векторов условие (3.8) выполняется не только при 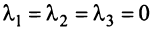 (а, например, при
(а, например, при 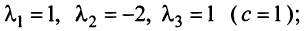 при
при 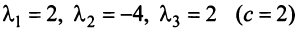 и т.д.), следовательно, эти векторы — линейно зависимые. ►
и т.д.), следовательно, эти векторы — линейно зависимые. ►
Определение. Линейное пространство  называется
называется 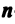 -мерным, если в нем существует я линейно независимых векторов, а любые из
-мерным, если в нем существует я линейно независимых векторов, а любые из 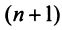 векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число
векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число  называется размерностью пространства
называется размерностью пространства  и обозначается
и обозначается 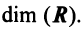
Определение. Совокупность  линейно независимых векторов
линейно независимых векторов  -мерного пространства
-мерного пространства  называется базисом. Справедлива следующая теорема.
называется базисом. Справедлива следующая теорема.
Теорема. Каждый вектор  линейного пространства
линейного пространства  можно представить
можно представить 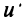 притом единственным способом в виде линейной комбинации векторов базиса.
притом единственным способом в виде линейной комбинации векторов базиса.
 Пусть векторы
Пусть векторы 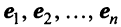 образуют произвольный базис
образуют произвольный базис  -мерного пространства
-мерного пространства  . Так как любые из (
. Так как любые из ( +1) векторов
+1) векторов  -мерного пространства R зависимы, то будут зависимы, в частности, векторы
-мерного пространства R зависимы, то будут зависимы, в частности, векторы 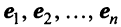 и рассматриваемый вектор
и рассматриваемый вектор  . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа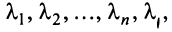 что
что
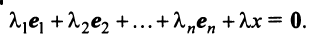
При этом 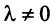 , ибо в противном случае, если
, ибо в противном случае, если 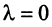 и хотя бы одно из чисел
и хотя бы одно из чисел 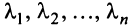 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 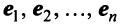 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
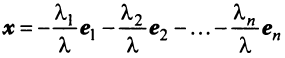 или
или
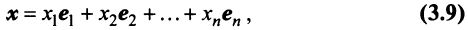
где 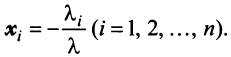
Это выражение 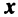 через
через  единственное, так как если допустить какое-либо другое выражение, например,
единственное, так как если допустить какое-либо другое выражение, например,
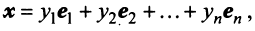 то, вычитая из него почленно (3.9), получим
то, вычитая из него почленно (3.9), получим
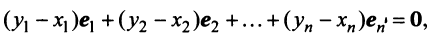 откуда из условия линейной независимости векторов
откуда из условия линейной независимости векторов следует, что '
следует, что '
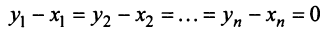 или
или
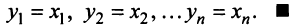
Равенство (3.9) называется разложением вектора  по базису
по базису  , а числа
, а числа 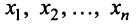 — координатами вектора
— координатами вектора  относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
относительно этого базиса. В силу единственности разложения (3.9) каждый вектор однозначно может быть определен координатами в некотором базисе.
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если  — система линейно независимых векторов пространства
— система линейно независимых векторов пространства  и любой вектор
и любой вектор 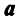 линейно выражается через
линейно выражается через  , то пространство
, то пространство  является n-мерным, а векторы
является n-мерным, а векторы  — его базисом.
— его базисом.
 Возьмем произвольные
Возьмем произвольные 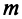 векторов пространства
векторов пространства  , где
, где 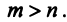 По условию каждый из них можно линейно выразить через
По условию каждый из них можно линейно выразить через  :
:
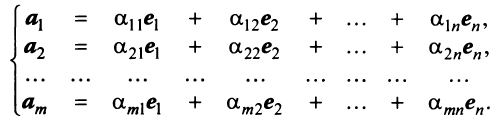 Рассмотрим матрицу
Рассмотрим матрицу 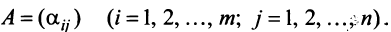
Ранг этой матрицы не превосходит 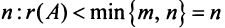 , следовательно, среди ее строк не более
, следовательно, среди ее строк не более 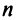 линейно независимых. Так как
линейно независимых. Так как 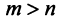 , то
, то 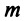 строк этой матрицы, а значит, и
строк этой матрицы, а значит, и 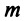 векторов
векторов 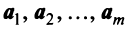 линейно зависимы. Таким образом, пространство
линейно зависимы. Таким образом, пространство 
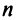 -мерно и
-мерно и  — его базис. ■
— его базис. ■
Пример:
В базисе 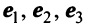 заданы векторы
заданы векторы 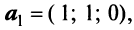
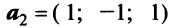 и
и 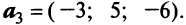 Показать, что векторы
Показать, что векторы 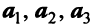 образуют базис.
образуют базис.
Решение:
Векторы 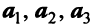 образуют базис, если они линейно независимы. Составим векторное равенство:
образуют базис, если они линейно независимы. Составим векторное равенство: 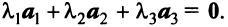 Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении:
Решая его аналогично примеру 3.2, можно убедиться в единственном нулевом его решении: 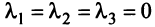 , т.е. векторы
, т.е. векторы 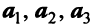 образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
образуют систему линейно независимых векторов и, следовательно, составляют базис. ►
Переход к новому базису
Пусть в пространстве  имеются два базиса: старый
имеются два базиса: старый  и новый
и новый 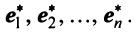 Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса: 
Полученная система означает, что переход от старого базиса  кновому
кновому 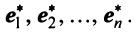 задается матрицей перехода
задается матрицей перехода 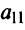 и тд.
и тд. 
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 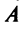 — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса
— неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 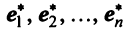 к старому базису
к старому базису 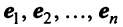 осуществляется с помощью обратной матрицы
осуществляется с помощью обратной матрицы 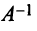 .
.
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 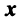 имеет координаты
имеет координаты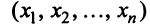 относительно старого базиса и координаты
относительно старого базиса и координаты 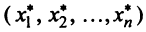 относительно нового базиса, т.е.
относительно нового базиса, т.е.
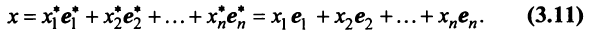
Подставив значения 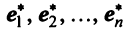 из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
из системы (3.10) в левую часть равенства (3.11), получим после преобразований:
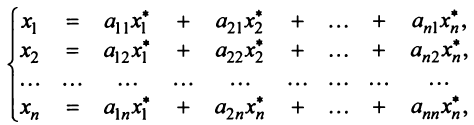
т.е. в матричной форме
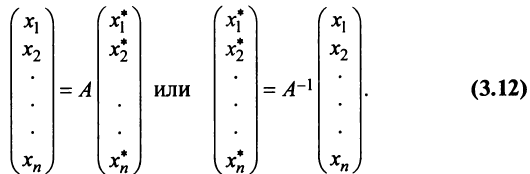
Пример:
По условию примера 3.3 вектор 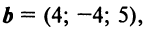 заданный в базисе
заданный в базисе  , выразить в базисе
, выразить в базисе  .
.
Решение:
Выразим связь между базисами: 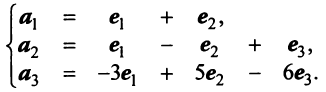
Матрица перехода от базиса 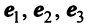 к базису
к базису 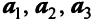 имеет вид
имеет вид 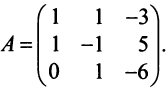 Вычисляем
Вычисляем 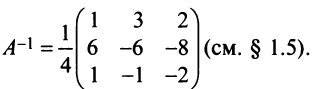 Теперь по (3.12)
Теперь по (3.12) 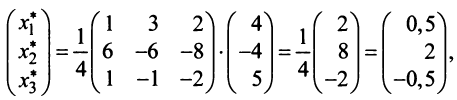
т.е. новые координаты вектора  в базисе
в базисе  есть 0,5; 2 и -0,5 и вектор
есть 0,5; 2 и -0,5 и вектор 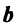 может быть представлен в виде:
может быть представлен в виде: 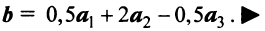
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов 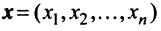 и
и 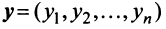 называется число
называется число
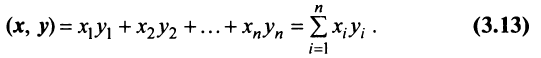
Скалярное произведение имеет экономический смысл. Если 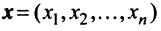 есть вектор объемов различных товаров, а
есть вектор объемов различных товаров, а 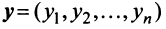 вектор их цен, то скалярное произведение
вектор их цен, то скалярное произведение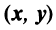 выражает суммарную стоимость этих товаров.
выражает суммарную стоимость этих товаров.
Скалярное произведение имеет следующие свойства:
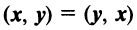 — коммутативное свойство;
— коммутативное свойство;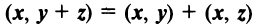 — дистрибутивное свойство;
— дистрибутивное свойство;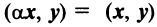 — для любого действительного числа;
— для любого действительного числа;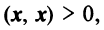 если
если 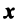 — ненулевой вектор;
— ненулевой вектор; 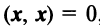 , если
, если 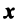 — нулевой вектор.
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 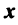 в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
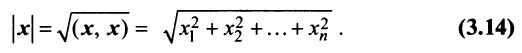
Имеют место следующие свойства длины вектора:
1. 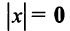 тогда и только тогда, когда
тогда и только тогда, когда 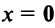 ;
;
2. 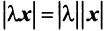 , где
, где 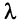 — действительное число;
— действительное число;
3. 
(неравенство Коши—Буняковского);
4. 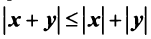 (неравенство треугольника).
(неравенство треугольника).
Угол 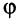 между двумя векторами
между двумя векторами  и
и 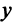 определяется равенством
определяется равенством
 где
где 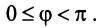
Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 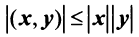 , т.е.
, т.е. 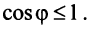
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 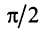 (ибо
(ибо 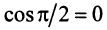 ).
).
Векторы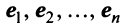
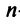 -мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если
-мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, и ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если 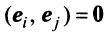 при
при 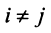 и |
и |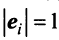 при
при 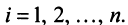
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 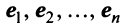 образуют один из базисов рассматриваемого
образуют один из базисов рассматриваемого 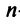 -мерного пространства
-мерного пространства  (т.е.
(т.е. 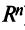 ). Для этого достаточно показать, что векторы
). Для этого достаточно показать, что векторы 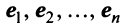 линейно независимы, т.е. равенство
линейно независимы, т.е. равенство
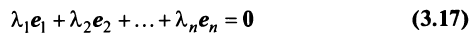
справедливо лишь при 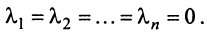
Действительно, умножая скалярно равенство (3.17) на любой вектор 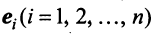 , получим
, получим
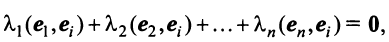
откуда, учитывая, что 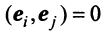 при
при 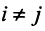 и
и 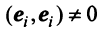 при всех
при всех 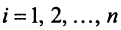 , вытекает, что
, вытекает, что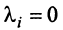 при всех
при всех 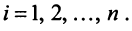
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 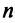 -мерном евклидовом пространстве существует ортонормированный базис.
-мерном евклидовом пространстве существует ортонормированный базис.
Примером ортонормированного базиса является система 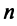 единичных векторов
единичных векторов 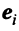 у которых
у которых 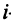 -я компонента равна единице, а остальные компоненты равны нулю:
-я компонента равна единице, а остальные компоненты равны нулю: 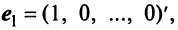
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства:  размерности
размерности 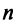 и
и  размерности
размерности 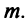
Определение. Если задан закон (правило), по которому каждому вектору  пространства
пространства  ставится в соответствие единственный вектор у пространства
ставится в соответствие единственный вектор у пространства  , то говорят, что задан оператор (преобразование, отображение)
, то говорят, что задан оператор (преобразование, отображение) 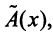 действующий из
действующий из  в
в  , и записывают
, и записывают 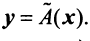
Оператор (преобразование) называется линейным, если для любых векторов  и
и 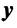 пространства
пространства  и любого числа
и любого числа 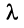 выполнился соотношения:
выполнился соотношения:
- 1.
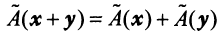 — свойство аддитивности оператора;
— свойство аддитивности оператора; - 2.
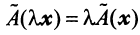 — свойство однородности оператора.
— свойство однородности оператора.
Вектор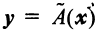 называется образом вектора
называется образом вектора  , а сам вектор
, а сам вектор  — прообразом вектора
— прообразом вектора 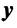 .
.
Если пространства  и
и  совпадают, то оператор
совпадают, то оператор  отображает пространство
отображает пространство  в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
Выберем в пространстве  базис eh
базис eh  и, учитывая (3.9), запишем разложение произвольного вектора
и, учитывая (3.9), запишем разложение произвольного вектора 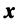 по данному базису:
по данному базису:
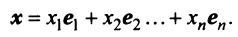
В силу линейности оператора  получаем
получаем
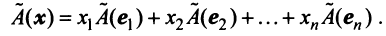
Поскольку 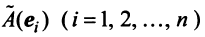 — также вектор из
— также вектор из  , то его можно разложить по базис
, то его можно разложить по базис . Пусть
. Пусть
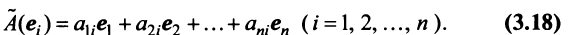
Тогда
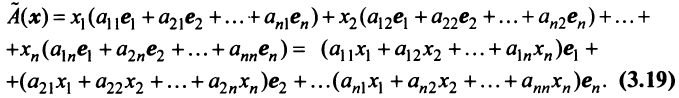
С другой стороны, вектор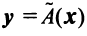 , имеющий в том же базисе
, имеющий в том же базисе  координаты
координаты 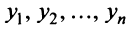 , можно записать так:
, можно записать так:
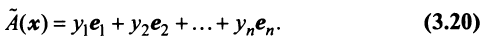
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
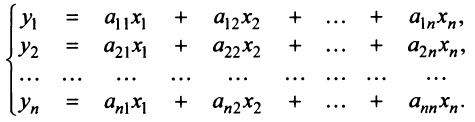
Матрица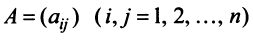 называется матрицей оператора
называется матрицей оператора  в базисе
в базисе  , а ранг
, а ранг 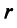 матрицы
матрицы 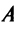 — рангом оператора
— рангом оператора  .
.
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 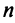 -го порядка соответствует линейный оператор
-го порядка соответствует линейный оператор 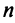 -мерного пространства.
-мерного пространства.
Связь между вектором 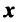 и его образом
и его образом 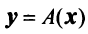 можно выразить в матричной форме уравнением
можно выразить в матричной форме уравнением

где 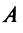 — матрица линейного оператора,
— матрица линейного оператора, 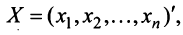
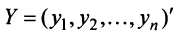 - матрицы-столбцы из координат векторов
- матрицы-столбцы из координат векторов  и
и 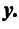
Пример:
Пусть в пространстве 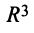 линейный оператор
линейный оператор  в базисе
в базисе 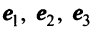 задан матрицей
задан матрицей 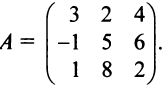 Найти образ
Найти образ 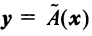 вектора
вектора 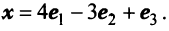
Решение:
По формуле (3.21) имеем 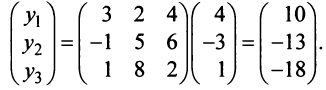
Следовательно, 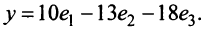 ►
►
Определим действия над линейными операторами.
Суммой двух линейных операторов 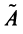 и
и 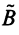 называется оператор
называется оператор 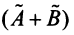 , определяемый равенством:
, определяемый равенством: 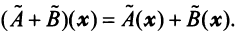
Произведением линейного оператора  на число
на число 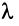 называется оператор
называется оператор 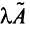 , определяемый равенством
, определяемый равенством 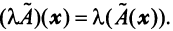
Произведением линейных операторов 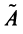 и
и 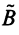 называется оператор
называется оператор 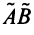 , определяемый равенством:
, определяемый равенством: 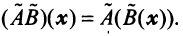
Можно убедиться в том, что операторы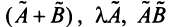 , полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
, полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
Определим нулевой оператор 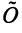 , переводящий все векторы пространства
, переводящий все векторы пространства 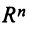 в нулевые векторы
в нулевые векторы 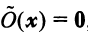 , и тождественный оператор
, и тождественный оператор 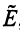 , действующий по правилу:
, действующий по правилу: 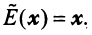
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы  и
и 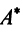 линейного оператора
линейного оператора  в базисах
в базисах 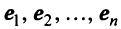 и
и 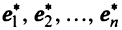 связаны соотношением
связаны соотношением

где 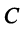 — матрица перехода от старого базиса к новому.
— матрица перехода от старого базиса к новому.
 При воздействии линейного оператора
При воздействии линейного оператора  вектор
вектор  пространства
пространства 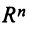 переводится в вектор
переводится в вектор 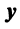 этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство
этого пространства, т.е. справедливо равенство (3.21) (в старом базисе) и равенство

(в новом базисе). Так как 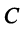 — матрица перехода от старого базиса к новому, то в соответствии с (3.12)
— матрица перехода от старого базиса к новому, то в соответствии с (3.12)

Умножим равенство (3.24) слева на матрицу  , получим
, получим 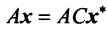 или с учетом (3.21)
или с учетом (3.21) 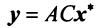 . Заменив левую часть полученного выражения в соответствии с (3.25), имеем:
. Заменив левую часть полученного выражения в соответствии с (3.25), имеем: 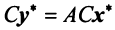 или
или 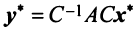 . Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22).
. Сравнивая найденное выражение с (3.23), мы получим доказываемую формулу (3.22). 
Пример:
В базисе 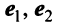 оператор (преобразование)
оператор (преобразование)  имеет матрицу
имеет матрицу 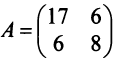 . Найти матрицу оператора
. Найти матрицу оператора  в базисе
в базисе 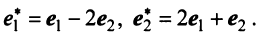
Решение:
Матрица перехода здесь 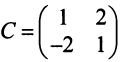 , а обратная к ней матрица
, а обратная к ней матрица 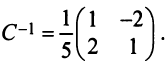 Следовательно, по (3.22)
Следовательно, по (3.22)
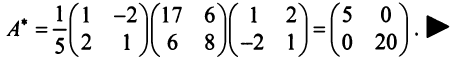
Собственные векторы и собственные значения линейного оператора
Определение. Вектор 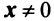 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если найдется такое число
, если найдется такое число 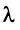 , что
, что

Число 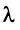 называется собственным значением оператора
называется собственным значением оператора  (матрицы
(матрицы  ), соответствующим вектору
), соответствующим вектору 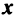 .
.
Из определения следует, что собственный вектор под действием линейного оператора  переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
Равенство (3.26) можно записать в матричной форме:

где вектор 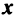 представлен в виде вектора-столбца, или в развернутом виде
представлен в виде вектора-столбца, или в развернутом виде
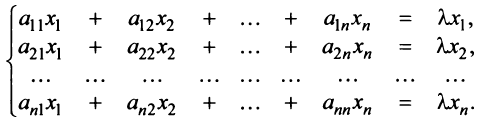
Перепишем систему так, чтобы в правых частях были нули:
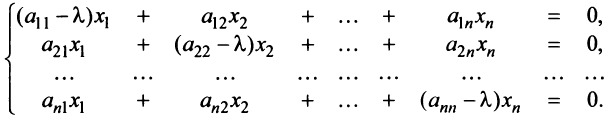
или в матричном виде
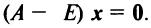
Полученная однородная система всегда имеет нулевое решение 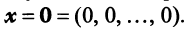 Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
Для существования ненулевого решения (см. § 2.5) необходимо и достаточно, чтобы определитель системы
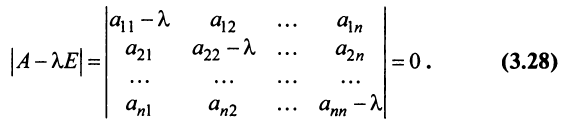
Определитель 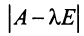 является многочленом
является многочленом 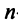 -й степени относительно
-й степени относительно 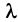 . Этот многочлен называется характеристическим многочленом оператора
. Этот многочлен называется характеристическим многочленом оператора  или матрицы
или матрицы  , а уравнение (3.28) — характеристическим уравнением оператора
, а уравнение (3.28) — характеристическим уравнением оператора  или матрицы
или матрицы  .
.
Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 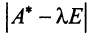 полученный в новом базисе
полученный в новом базисе 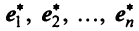 , если известна матрица
, если известна матрица 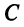 перехода от старого базиса
перехода от старого базиса 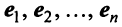 к новому. С учетом (3.22) получим
к новому. С учетом (3.22) получим
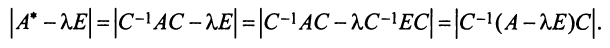
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
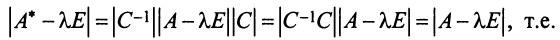
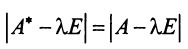 независимо от выбора базиса.
независимо от выбора базиса.
Пример:
Найти собственные значения и собственные векторы линейного оператора  , заданного матрицей
, заданного матрицей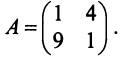
Решение:
Составляем характеристическое уравнение 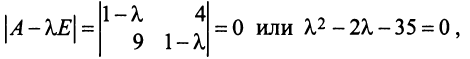
откуда собственные значения линейного оператора 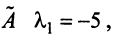
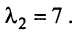
Находим собственный вектор 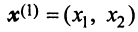 , соответствующий собственному значению
, соответствующий собственному значению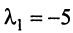 . Для этого решаем матричное уравнение
. Для этого решаем матричное уравнение
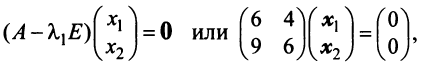 откуда находим
откуда находим 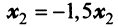 . Положив
. Положив 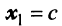 , получим, что векторы
, получим, что векторы 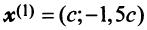 при любом
при любом 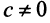 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 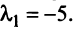
Аналогично можно убедиться в том, что векторы 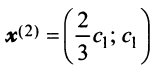 при любом
при любом 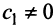 являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 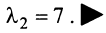
Наиболее простой вид принимает матрица 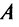 линейного оператора
линейного оператора  , имеющего
, имеющего 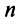 линейно независимых собственных векторов
линейно независимых собственных векторов 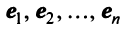 с собственными значениями, соответственно равными
с собственными значениями, соответственно равными 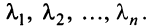 Векторы
Векторы 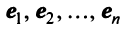 примем за базисные. Тогда
примем за базисные. Тогда 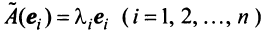 или с учетом (3.18)
или с учетом (3.18)
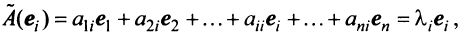
откуда 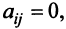 если
если 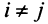 , и
, и 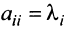 ,если
,если 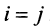 . Таким образом, матрица оператора
. Таким образом, матрица оператора  в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
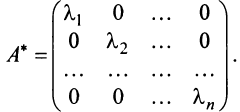 Верно и обратное: если матрица
Верно и обратное: если матрица 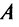 линейного оператора
линейного оператора  в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора
в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора  .
.
Можно доказать, что если линейный оператор имеет 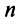 попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
Пример:
Привести матрицу 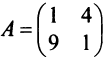 линейного оператора
линейного оператора  к диагональному виду.
к диагональному виду.
Решение:
В примере 3.7 были найдены собственные значения матрицы 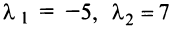 и соответствующие им собственные векторы
и соответствующие им собственные векторы 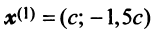 и
и 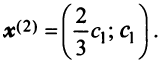 Так как координаты векторов
Так как координаты векторов 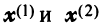 не пропорциональны, то векторы
не пропорциональны, то векторы 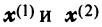 линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов
линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов 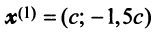 и
и 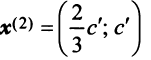 (т.е. при любых
(т.е. при любых 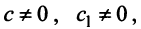 например при
например при 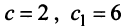 из векторов
из векторов 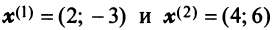 и т.д.), матрица
и т.д.), матрица 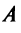 будет иметь диагональный вид:
будет иметь диагональный вид: 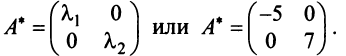 Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы
Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы 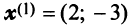 и
и 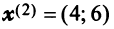 . Действительно, матрица
. Действительно, матрица 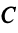 перехода от старого базиса к новому в этом случае будет иметь вид
перехода от старого базиса к новому в этом случае будет иметь вид 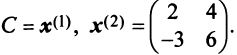 Тогда в соответствии с (3.22) матрица
Тогда в соответствии с (3.22) матрица 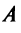 в новом базисе
в новом базисе 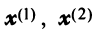 примет вид:
примет вид:
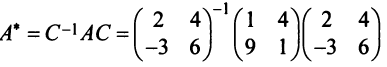
или после вычислений (которые мы опускаем) 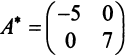
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 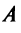 . ►
. ►
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 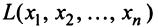 от
от 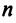 переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
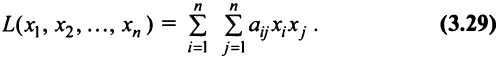
Предполагаем, что коэффициенты квадратичной формы 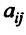 — действительные числа, причем
— действительные числа, причем 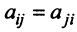 . Матрица
. Матрица 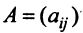
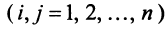 , составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:
, составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:

где 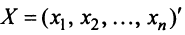 — матрица-столбец переменных. В самом деле :
— матрица-столбец переменных. В самом деле : 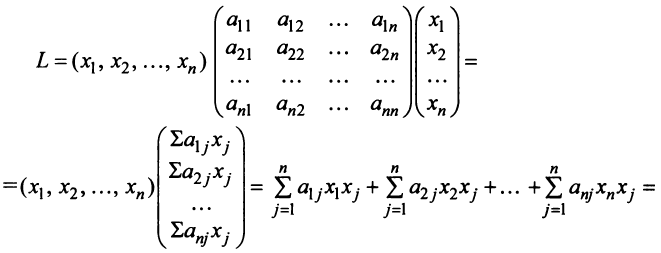
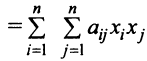 и эквивалентность формул (3.29) и (3.30) установлена.
и эквивалентность формул (3.29) и (3.30) установлена.
Пример:
Дана квадратичная форма 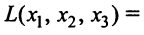
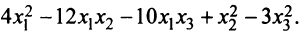 Записать ее в матричном виде.
Записать ее в матричном виде.
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
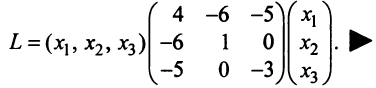
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 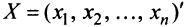 и
и 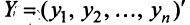 связаны линейным соотношением
связаны линейным соотношением 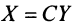 , где,
, где, 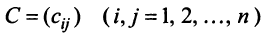 есть некоторая невырожденная матрица
есть некоторая невырожденная матрица 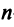 -го порядка. Тогда квадратичная форма
-го порядка. Тогда квадратичная форма
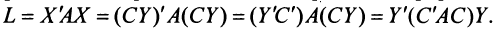
, Итак, при невырожденном линейном преобразовании 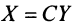 матрица квадратичной формы принимает вид:
матрица квадратичной формы принимает вид:

Пример:
Дана квадратичная форма 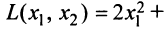
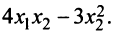 Найти квадратичную форму
Найти квадратичную форму 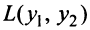 , полученную из данной линейным преобразованием
, полученную из данной линейным преобразованием 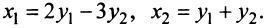
Решение:
Матрица данной квадратичной формы 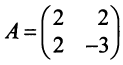 , а матрица линейного преобразования
, а матрица линейного преобразования 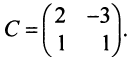
Следовательно, по (3.31) матрица искомой квадратичной формы 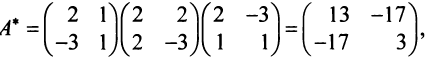 а квадратичная форма имеет вид
а квадратичная форма имеет вид 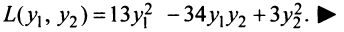
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 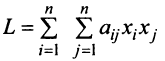 , называется канонической (или имеет канонический вид), если все ее коэффициенты
, называется канонической (или имеет канонический вид), если все ее коэффициенты 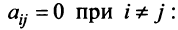
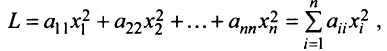
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
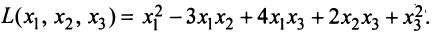
Решение:
Вначале вьделим полный квадрат при переменной 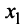 , коэффициент при квадрате которой отличен от нуля:
, коэффициент при квадрате которой отличен от нуля:
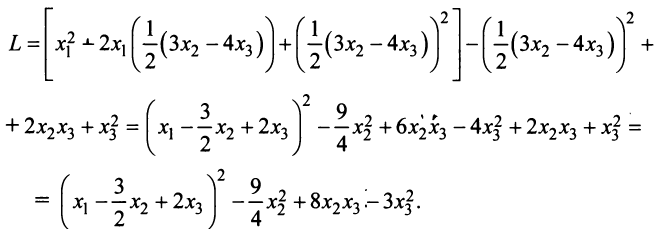
Теперь выделяем полный квадрат при переменной 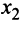 , коэффициент при которой отличен от нуля:
, коэффициент при которой отличен от нуля:
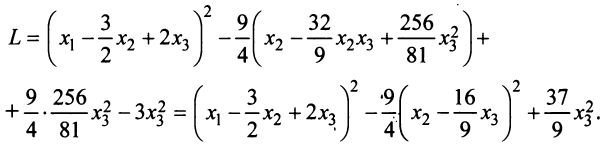 Итак, невырожденное линейное преобразование
Итак, невырожденное линейное преобразование
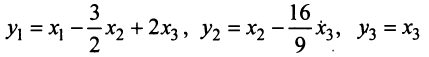
приводит данную квадратичную форму к каноническому виду
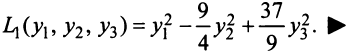
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 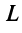 в примере 3.10 можно было привести к виду
в примере 3.10 можно было привести к виду
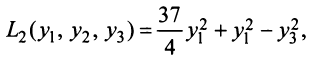
применив невырожденное линейное преобразование
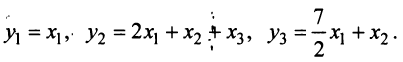
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 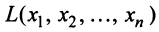 называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
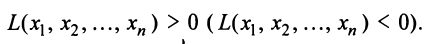
Так, например, квадратичная форма 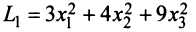 является положительно определенной, а форма
является положительно определенной, а форма 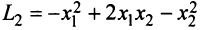 — отрицательно определенной.
— отрицательно определенной.
Теорема. Для того чтобы квадратичная форма 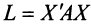 была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 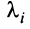 матрицы
матрицы 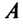 были положительны (отрицательны).
были положительны (отрицательны).
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 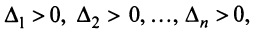 где
где
 Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. '
Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка. '
Пример:
Доказать, что квадратичная форма 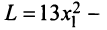
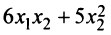 является положительно определенной.
является положительно определенной.
Решение:
Первый способ. Матрица  квадратичной формы имеет вид
квадратичной формы имеет вид 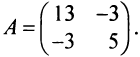 Для матрицы
Для матрицы характеристическое
характеристическое
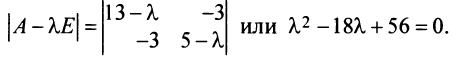
Решая уравнение, найдем 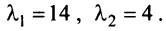 Так как корни характеристического уравнения матрицы
Так как корни характеристического уравнения матрицы  положительны, то на основании приведенной теоремы квадратичная форма
положительны, то на основании приведенной теоремы квадратичная форма 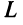 — положительно определенная.
— положительно определенная.
Второй способ. Так как главные миноры матрицы 
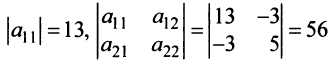 положительны, то по критерию Сильвестра данная квадратичная форма
положительны, то по критерию Сильвестра данная квадратичная форма 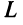 положительно определенная. ►
положительно определенная. ►
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 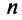 стран
стран 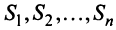 , национальный доход каждой из которых равен соответственно
, национальный доход каждой из которых равен соответственно 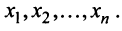 Обозначим коэффициентами
Обозначим коэффициентами 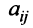 долю национального дохода, которую страна
долю национального дохода, которую страна 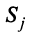 тратит на покупку товаров у страны
тратит на покупку товаров у страны 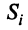 . Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
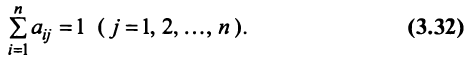
Рассмотрим матрицу 
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 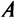 равна 1.
равна 1.
Для любой страны 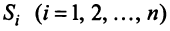 выручка от внутренней и внешней торговли составит:
выручка от внутренней и внешней торговли составит: 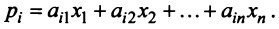
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 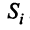 , т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
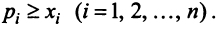
Если считать, что 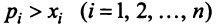 , то получаем систему неравенств
, то получаем систему неравенств
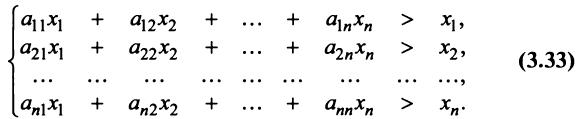
Сложив все неравенства системы (3.33), получим после группировки 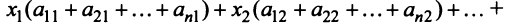
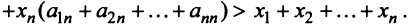
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
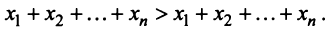
Таким образом, неравенство 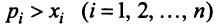 невозможно, и условие
невозможно, и условие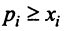 , принимает вид
, принимает вид 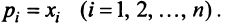 (С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
(С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
Вводя вектор 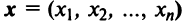 национальных доходов стран, получим матричное уравнение
национальных доходов стран, получим матричное уравнение

В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы 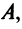 отвечающего собственному значению
отвечающего собственному значению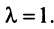
Пример:
Структурная матрица торговли трех стран 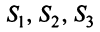 имеет вид:
имеет вид:
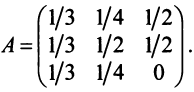
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 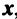 , отвечающий собственному значению
, отвечающий собственному значению 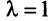 , решив уравнение
, решив уравнение 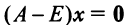 или систему
или систему
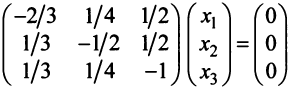
методом Гаусса. Найдем 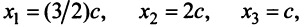 т.е.
т.е. 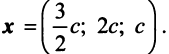 Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
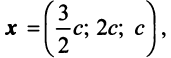 т.е. при соотношении национальных доходов стран
т.е. при соотношении национальных доходов стран 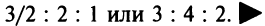
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |