Электромеханические аналогии

Электромеханические аналогии:

Явления, исследуемые на основе законов физики, описываются математически при помощи систем уравнений. Исходя из единства уравнений, соответствующих некоторым двум явлениям, происходящим в различных областях, например в электрической цепи и механической системе, можно установить аналогию между этими явлениями. «Единство природы обнаруживается в «поразительной аналогичности» дифференциальных уравнений, относящихся к различным областям явлений»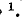

Благодаря единству уравнений электрических и механических систем исследование явлений в механической системе может быть заменено исследованием процессов в электрической цепи. Выполнение электрических цепей обычно сопряжено с меньшими трудностями, чем выполнение механических систем; они более компактны и, что особенно важно, измерения в них более точны и удобны. Процессы в электромеханических системах, представляющих совокупность электрических и механических устройств, также могут с успехом исследоваться с помощью электромеханических аналогий.

Механические системы с сосредоточенными параметрами, которые по аналогии с электрическими цепями будем называть механическими цепями, состоят из активных элементов (источников энергии) и пассивных элементов.

Рассмотрим идеализированные элементы простейших линейных механических цепей, совершающих поступательное или вращательное движение (комбинированное поступательно-вращательное движение опустим).

В случае поступательного движения заданная внешняя сила, приложенная к цепи, рассматривается как источник силы, а заданная скорость какой-либо точки цепи — как источник скорости.

В случае вращательного движения заданный вращающий момент, приложенный к цепи, рассматривается как источник момента, а заданная угловая скорость какой-либо точки — как источник угловой скорости .

Роль пассивных элементов в механических цепях выполняют массы, моменты инерции, пружины и механические (демпфирующие) сопротивления.

Массой называется идеализированный элемент механической цепи, обладающий инерцией. В нем накапливается кинетическая энергия. При этом термин «масса» и соответствующее ему условное обозначение т применяются для обозначения как самого инерционного элемента, так и его количественной характеристики. Сила F (ньютон — H), приложенная к центру тяжести свободного твердого тела, сообщает ему линейную скорость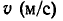

На вращение тела влияет не только масса, но и распределение ее относительно оси вращения. Поэтому вращающийся инерционный элемент характеризуется моментом инерции 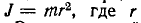— радиус инерции тела относительно оси вращения. Это пассивный элемент, в котором накапливается кинетическая энергия вращения.

Момент 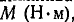приложенный к свободному твердому телу, сообщает ему угловую скорость со (рад/с) и угловое ускорение 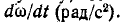Если момент инерции постоянен, то
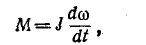(7-34)
т. е. момент инерции 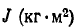представляет собой коэффициент пропорциональности между моментом и угловым ускорением.

Кинетическая энергия поступательного движения равна 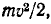а кинетическая энергия вращательного движения 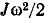(Дж).

Пружина играет роль пассивного элемента, в котором накапливается потенциальная энергия, Сила натяжения или давления, развиваемая соответственно растянутой или сжатой пружиной при данном относительном перемещении х (м) ее конца, пропорциональна ее жесткости К, измеряемой в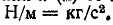

Сила F, необходимая для относительного перемещения х конца пружины, действует вдоль оси х и равна по закону Гука:

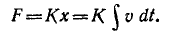
Продифференцировав обе части уравнения, получим:

Величина, обратная К, называется податливостью пружины. Момент, необходимый для создания углового перемещения 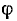конца пружины, подвергающейся скручиванию, пропорционален жесткости К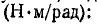

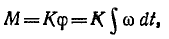
откуда

В этом случае коэффициент пропорциональности 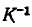называется податливостью при кручении.

Потенциальная энергия при растяжении или сжатии пружины равна 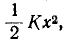а потенциальная энергия при скручивании 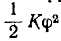(Дж).

Демпфирующее механическое сопротивление создается вязким трением. Вследствие механического сопротивления происходит необратимый процесс преобразования кинетической энергии в тепло.

В линейной механической цепи с поступательным движением сила трения пропорциональна первой степени относительной скорости точек, принадлежащих трущимся поверхностям:

где f—коэффициент трения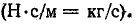

При вращательном движении момент силы трения пропорционален первой степени относительной угловой скорости:

В этом случае коэффициент трения f измеряется в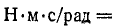

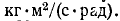
Мощность, расходуемая на трение, равна при поступательном движении 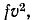а при вращательном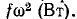

Сопоставление уравнений (7-33) — (7-38) с уравнениями элементов электрических цепей

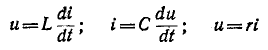
показывает, что механическая сила и вращающий момент соответствуют напряжению, линейная и угловая скорости — юку, масса и момент инерции — индуктивности, податливость пружины — емкости, механическое сопротивление — сопротивлению,

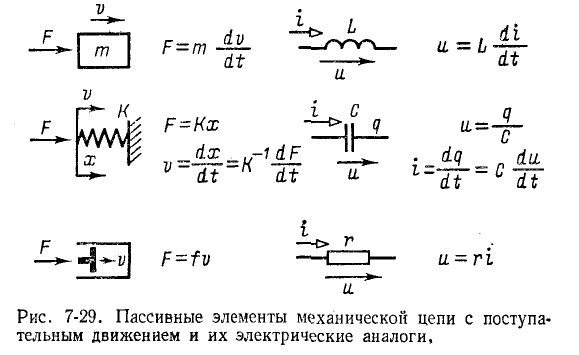
На рис. 7-29 приведены изображения пассивных элементов механической цепи с поступательным движением и показаны их электрические аналоги.

Рассмотренная система электромеханических аналогий, сведенная в табл. 7-1, не является единственной. Взяв дуальную электрическую цепь, можно заключить, что механическая сила и вращающий момент соответствуют току, линейная и угловая скорости — напряжению, Масса и момент инерции — емкости, податливость пружины — индуктивности, механическое сопротивление — проводимости.

Дифференциальные уравнения движения механической цепи могут быть выведены на основе второго закона Ньютона, который для поступательного движения гласит: если на тело действует несколько сил, то его ускорение совпадает по направлению с равнодействующей этих сил и пропорционально отношению последней к массе тела.                

Для вращательного движения применяется следующая формулировка второго закона Ньютона: если относительно оси вращения тела действует несколько моментов, то его угловое ускорение относительно той же оси пропорционально отношению результирующего момента к моменту инерции тела.

Дифференциальные уравнения движения механической цепи могут быть также получены на основании принципа Даламбера: при движении тела действующие на него силы и сила инерции удовлетворяют уравнению равновесия сил.

Уравнения такого же типа, получаемые для электрических цепей на основании законов Кирхгофа, могут быть либо уравнениями напряжений, либо уравнениями токов.

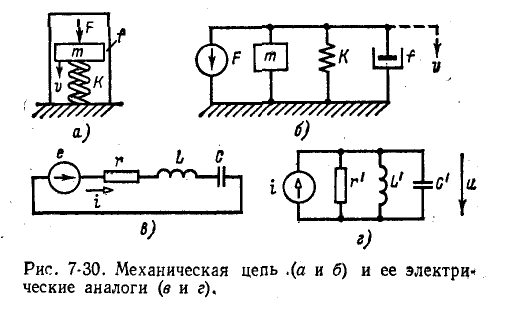
В качестве примера рассмотрим простейшую механическую систему: масса ш находится под воздействием силы F и опирается на пружину (рис, 7-30, а). Тело движется между неподвижными направляющими, и между ним и направляющими- возникает вязкое трение, Массой пружины пренебрегаем.

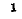Механическое сопротивление изображается в виде демпфера.

На рис. 7-30. б изображена схема данной механической цепи. По второму закону Ньютона

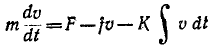
или

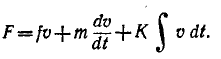
Пользуясь первой системой электромеханических аналогий (сила — напряжение, табл. 7-1), получаем уравнение электрической цепи, показанной на рис. 7-30, в:

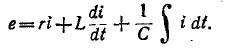
В свою очередь, применив вторую систему аналогий (сила — ток), получим уравнение электрической цепи, показанной на рис, 7-30, г:

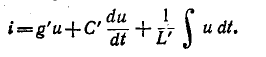
Таким образом, можно пользоваться двумя системам» электромеханических аналогий: в одной из них напряжение, а в другой — ток являются аналогом силы или вращающего момента. Две электрические цепи, аналогичные одной и той же механической цепи, являются дуальными, так как контурные токи одной цепи соответствуют узловым напряжениям другой.

Электромеханические аналогии находят практическое применение в электрических моделях.