Электромагнитная индукция в физике - формулы и определение с примерами

Содержание:

Электромагнитная индукция:

Как вы уже знаете, между заряженными телами (частицами), кроме гравитационного, существует и электромагнитное взаимодействие. Если заряды покоятся относительно определённой инерциальной системы отсчёта, электромагнитное взаимодействие между ними называют электростатическим. При движении электрически заряженных тел (частиц) проявляется составляющая электромагнитного взаимодействия — магнитное взаимодействие.

В этой главе вы познакомитесь с явлениями, в которых важную роль играет магнитное взаимодействие, обусловленное существованием магнитного поля, создаваемого постоянными магнитами, электрическим током или изменяющимся во времени электрическим полем.

Действие магнитного поля на проводник с током. Взаимодействие проводников с током

То, что магниты взаимодействуют друг с другом, причём разноимённые полюса магнитов притягиваются, а одноимённые — отталкиваются (рис. 180), что распиленный пополам магнит превращается в два магнита, а железо при соприкосновении с магнитом намагничивается, впервые описал французский учёный Пьер де Мерикур в трактате «Письмо о магните» (1269 г.).

В 1759 г. на взаимосвязь электричества и магнетизма указал Ф. Эпинус в трактате «Опыт теории электричества и магнетизма». В 8 классе вы узнали, что английский естествоиспытатель и придворный лекарь Уильям Гильберт (1544—1603) в трактате «О магните, магнитных телах и о большом магните — Земле. Новая физиология, доказанная множеством аргументов и опытов» (1600 г.),

Как вы уже знаете, между заряженными телами (частицами), кроме гравитационного, существует и электромагнитное взаимодействие. Если заряды покоятся относительно определённой инерциальной системы отсчёта, электромагнитное взаимодействие между ними называют электростатическим. При движении электрически заряженных тел (частиц) проявляется составляющая электромагнитного взаимодействия — магнитное взаимодействие.

Вы познакомитесь с явлениями, в которых важную роль играет магнитное взаимодействие, обусловленное существованием магнитного поля, создаваемого постоянными магнитами, электрическим током или изменяющимся во времени электрическим полем.

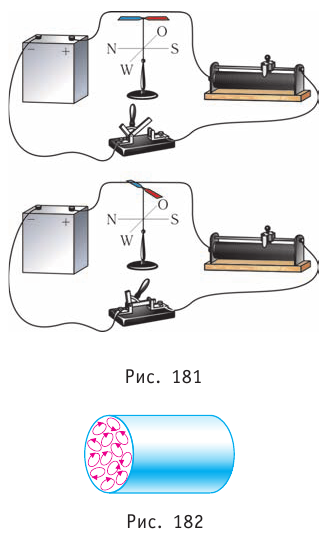
Открытие Эрстеда позволило Амперу сделать вывод, что магнитные свойства любого тела определяются замкнутыми электрическими токами, циркулирующими внутри этого тела и получившими название «амперовы токи» или «молекулярные токи» (рис. 182). Это означало, что магнитное взаимодействие обусловлено не особыми магнитными зарядами, а движением электрических зарядов — электрическим током.

Магнитное поле

Взаимодействие проводника с током и магнитной стрелки в опыте Эрстеда является взаимодействием электрического тока проводника с «амперовыми токами» в магнитной стрелке (гипотеза Ампера). Это взаимодействие осуществляется посредством магнитного поля.

Опыты показывают, что магнитное поле возникает при движении любых электрических зарядов — свободных электронов металлического проводника, ионов электролита и газа, электронов и дырок полупроводника, связанных зарядов при движении заряженного диэлектрика. Поскольку скорость движения заряда зависит от выбора системы отсчёта, магнитное поле одного и того же заряда в разных системах отсчёта будет различным. Если по отношению к определённой инерциальной системе отсчёта электрический заряд покоится, то в этой системе отсчёта он создаёт только электростатическое поле. Электрический заряд, движущийся относительно данной инерциальной системы отсчёта, создаёт в ней не только электрическое поле, но и магнитное, являющиеся компонентами единого электромагнитного поля.

Согласно представлениям классической электродинамики магнитное поле — особая форма материи, созданная движущимися (относительно определённой инерциальной системы отсчёта) электрическими зарядами или переменными электрическими полями. Посредством магнитного поля осуществляется взаимодействие между подвижными электрическими зарядами (а также магнитами). Иначе говоря, каждый движущийся в данной инерциальной системе отсчёта электрический заряд создаёт в окружающем пространстве магнитное поле, которое действует с некоторыми силами на любые другие движущиеся в данном магнитном поле электрические заряды (постоянные магниты). Таким образом, о существовании магнитного поля можно судить по наличию силы, действующей на электрический заряд, движущийся относительно выбранной инерциальной системы отсчёта.

Современные научные представления не отвергают, а, наоборот, предсказывают частицы с магнитным зарядом — магнитные монополи. Однако такие частицы пока экспериментально не наблюдали.

Силы, действующие со стороны магнитного поля на находящиеся в нём проводники с током или движущиеся заряды, в дальнейшем будем называть магнитными силами.

Действие магнитного поля на проводник с током

Поскольку магнитное поле проводника с током действует с определённой силой на магнит (в опыте Эрстеда — на магнитную стрелку), то естественно предположить, что со стороны магнитного поля магнита на проводник с током должна действовать сила. Это предположение можно проверить на опытах.

Соберём электрическую цепь, изображённую на рисунке 183, а. При разомкнутой цепи действия со стороны магнитного поля дугообразного магнита на гибкий проводник не наблюдается. При замыкании цепи проводник приходит в движение: он либо втягивается в пространство между полюсами дугообразного магнита (рис. 183, б), либо выталкивается из него (рис. 183, в) при обратном расположении полюсов магнита (или при изменении направления тока).

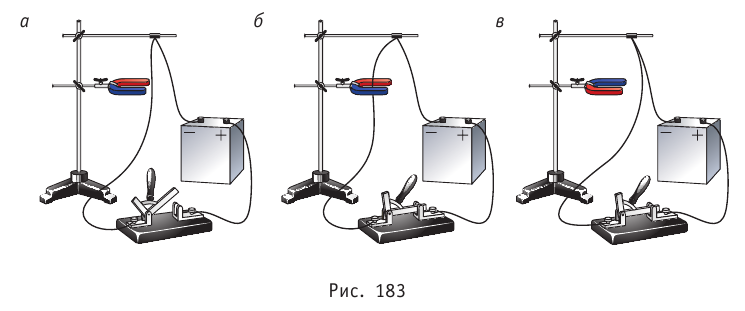
Этот опыт ещё раз доказывает, что магнитное поле действует только на движущиеся заряды.

Действует ли магнитное поле на заряженные частицы, движущиеся в вакууме? Пусть в катодной трубке (рис. 184, а) от катода К к аноду А движется пучок электронов. В отсутствие внешнего магнитного поля он будет двигаться прямолинейно и перпендикулярно к поверхности анода. Если к трубке поднести магнит (рис. 184, б), то электронный пучок отклонится вниз. Поменяв местами расположение полюсов магнита, можно отклонить пучок вверх. Траектория электронов внутри трубки доступна наблюдению благодаря экрану Э, покрытому люминофором — веществом, светящимся под воздействием ударов электронов о него.

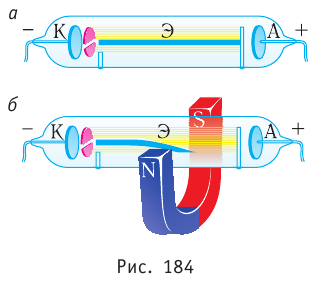
Во всех рассмотренных случаях на проводники с током (движущиеся заряженные частицы) действовала магнитная сила, которую можно рассматривать как результат взаимодействия магнитного поля постоянного магнита с магнитным полем проводника с током (движущихся заряженных частиц).

Взаимодействие проводников с током

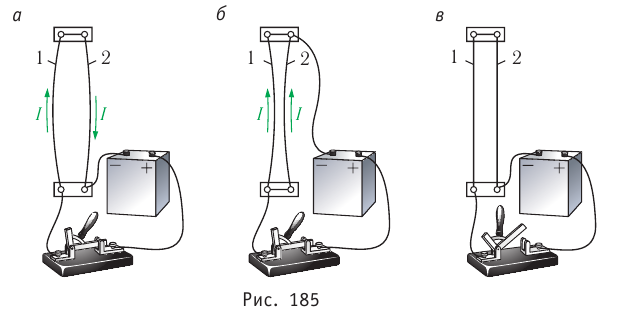
Открытие Эрстеда дало толчок к исследованиям по установлению связи между электрическими и магнитными явлениями. Ампер в 1820 г. провёл ряд экспериментов по изучению взаимодействия двух гибких первоначально параллельных и прямолинейных проводников с током. Ампер установил, что в случае, когда токи в проводниках проходят в противоположных направлениях, проводники отталкиваются (рис. 185, а), а когда в одном направлении — притягиваются (рис. 185, б). При отсутствии токов в проводниках они не взаимодействуют (рис. 185, в).

Магнитное поле одного проводника с током взаимодействует с током другого проводника посредством магнитной силы.

 Если рассматривать взаимодействие проводников с током более детально, то надо отметить, что оно имеет как магнитную, так и электрическую компоненты. Электрическое взаимодействие обусловлено зарядами, которые находятся на поверхности проводников с током. Утверждение о том, что проводники с токами одного направления притягиваются, является верным только в том случае, когда электрическое взаимодействие между проводниками значительно слабее, чем магнитное, т. е. если сопротивление проводников мало, а сила тока в них достаточна велика.
Магнитное взаимодействие двух параллельных проводников с током используют в СИ для определения единицы силы тока — ампера (А).

1 А — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии I м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, модуль которой равен 2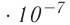 на каждый метр длины.

Действие магнитного поля на рамку с током

Действие магнитного поля на проводник с током не всегда проявляется в притяжении или отталкивании. В этом можно убедиться на опыте. Подвесим на некотором расстоянии от проводника на тонких и гибких подводящих проводах маленькую (по сравнению с расстояниями, на которых магнитное поле заметно изменяется) рамку (рис. 186, а). При пропускании по проводнику и рамке электрического тока рамка повернётся и расположится так, что окажется в одной плоскости с проводником с током (рис. 186, б).

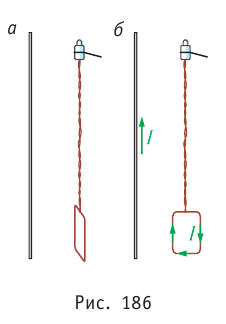
Действием магнитного поля на ток в подводящих проводах можно пренебречь, если они обвивают друг друга (см. рис. 186) или расположены близко друг к другу. Действительно, провода находятся в одной и той же области поля и по ним проходят токи одинаковой силы и противоположного направления. Таким образом, силы, действующие на ток в подводящих проводах со стороны магнитного поля, равны по модулю и противоположно направлены. Следовательно, подвес остаётся в покое. Рамка, расположенная в непосредственной близости от проводника, будет не только поворачиваться, но ещё и притягиваться к проводнику с током, так как вблизи проводника существенно проявляется неоднородность магнитного поля, создаваемого током в проводнике.

Ориентирующее действие на рамку с током оказывает не только магнитное поле проводника с током. Поместим проволочную рамку, способную свободно поворачиваться, между полюсами постоянного дугообразного магнита. Если по рамке проходит ток, она устанавливается так, что её плоскость перпендикулярна прямой, соединяющей полюса магнита (рис. 187). Таким образом, магнитное поле оказывает на рамку с током ориентирующее действие, такое же, как и на стрелку компаса.

1. Магнитное поле — особая форма материи, созданная движущимися (относительно определённой инерциальной системы отсчёта) электрическими зарядами или переменными электрическими полями.
2. Каждый движущийся электрический заряд создаёт в окружающем пространстве магнитное поле, которое действует с определёнными силами на любые другие движущиеся электрические заряды.
3. Магнитная сила — сила, которая действует со стороны магнитного поля на находящиеся в нём проводник с током, движущийся заряд или магнит.
4. 1 А — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, модуль которой равен 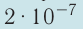Н на каждый метр длины.
5. Магнитное поле оказывает ориентирующее действие на рамку с током и на магнитную стрелку.

Индукция магнитного поля

Линии магнитной индукции:

Изучая электростатику, вы узнали, что распределение поля в пространстве можно сделать «видимым», пользуясь представлениями о линиях напряжённости. При изучении физики в 8 классе вы узнали, что магнитные поля также можно изображать графически в виде магнитных линий. Для описания магнитного поля введём его основную характеристику, аналогичную напряжённости 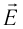электростатического поля. Такой характеристикой служит индукция магнитного поля 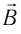(или магнитная индукция), которая является векторной величиной и позволяет определить силу, действующую на проводник с током (движущийся заряд) в магнитном поле.

Направление индукции магнитного поля

Для определения направления индукции магнитного поля 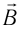используют ориентирующее действие магнитного поля на магнитную стрелку или рамку с током. Направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле, принимают за направление магнитной индукции.

Направление магнитной индукции 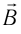в том месте магнитного поля, где расположена небольшая плоская рамка с током, совпадает с направлением положительной нормали 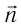к плоскости рамки. Направлением положительной нормали принято считать направление движения буравчика, рукоятку которого вращают в направлении тока в рамке. В исследуемом магнитном поле направление положительной нормали совпадает с направлением от южного полюса S к северному полюсу N магнитной стрелки (рис. 188).

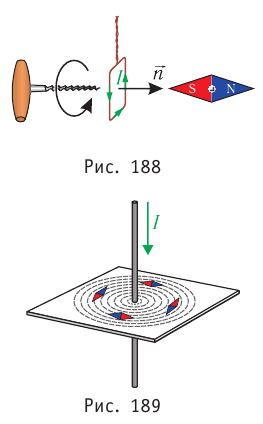
В магнитном поле прямолинейного проводника с током магнитные стрелки располагаются по касательным к окружностям (рис. 189), центры которых лежат на оси проводника.

На практике часто приходится иметь дело с магнитными полями электрических токов, проходящих по катушкам (соленоидам). В магнитном поле катушки с током магнитные стрелки устанавливаются по касательным к замкнутым кривым, охватывающим витки катушки (рис. 190).

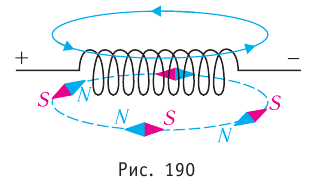
Линии магнитной индукции

Итак, исследуя магнитное поле, создаваемое проводником с током или постоянным магнитом, с помощью магнитной стрелки в каждой точке пространства можно определить направление магнитной индукции. Такое исследование позволяет графически представить пространственную структуру магнитного поля в виде линий магнитной индукции.

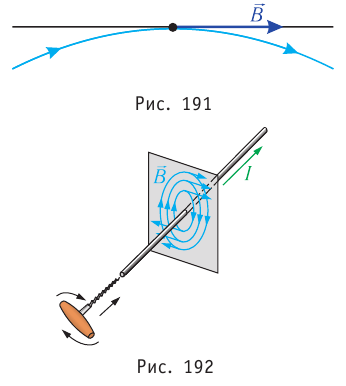
Линией индукции магнитного поля называют воображаемую линию в пространстве, касательная к которой совпадает с направлением индукции магнитного поля в каждой точке поля (рис. 191). Линии магнитной индукции непрерывны (не имеют ни начала, ни конца), замыкаются сами на себя. Это характерно для любых магнитных полей. Поля, обладающие таким свойством, называют вихревыми.

Очевидно, что через любую точку в магнитном поле можно провести только одну линию индукции. Поскольку индукция магнитного поля в любой точке пространства имеет определённое направление, то и направление линии индукции в каждой точке этого поля может быть только единственным. Это означает, что линии магнитной индукции, так же как и линии напряжённости электрического поля, не пересекаются.

Определить направление линий магнитной индукции можно, используя правило буравчика: если поступательное движение буравчика совпадает с направлением тока, то рукоятка буравчика поворачивается в направлении линий магнитной индукции. В случае прямолинейного проводника линии магнитной индукции представляют собой концентрические окружности, которые находятся в плоскостях, перпендикулярных к проводнику с током (рис. 192).

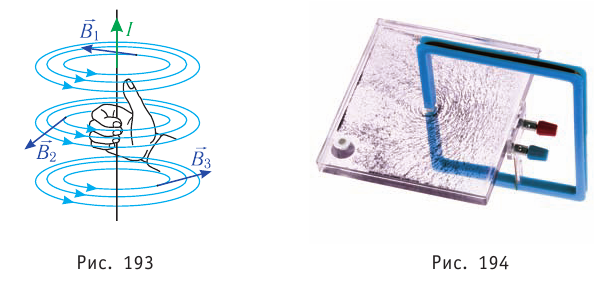
Определить направление линий индукции магнитного поля прямолинейного проводника с током можно также с помощью правила правой руки: если мысленно обхватить проводник правой рукой так, чтобы большой палец указывал направление тока, то остальные пальцы окажутся согнуты в направлении линий магнитной индукции (рис. 193).

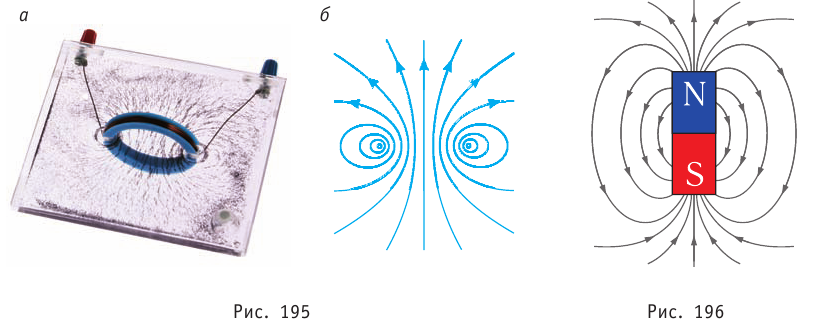
Картину линий магнитной индукции можно получить, используя мелкие железные опилки, которые в магнитном поле ведут себя, как магнитные стрелки. На рисунке 194 показана картина магнитного поля прямолинейного участка проводника с током. Картина магнитного поля кругового витка с током и графическое изображение линий магнитной индукции представлены на рисунке 195, а, б.

Полагают, что линии индукции магнитного поля, созданного постоянным магнитом, направлены внутри магнита от его южного полюса S к северному полюсу N (рис. 196).

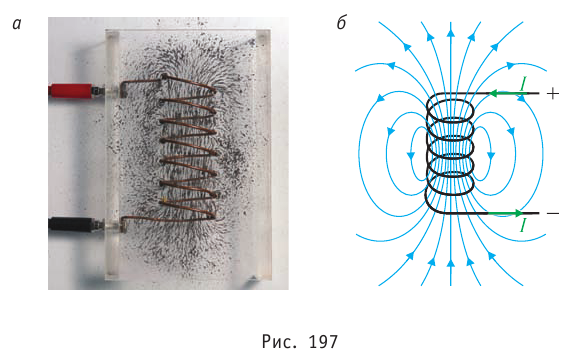
Магнитное поле соленоида с током подобно полю полосового магнита. На рисунке 197, а, б показана картина магнитного поля соленоида с током и дано графическое изображение линий индукции. Соленоид представляет собой цилиндрическую катушку, на которую виток к витку намотан провод. Если длина соленоида много больше его диаметра, то внутри центральной части соленоида линии индукции магнитного поля практически параллельны и направлены вдоль его оси. Расчётами можно показать, что численное значение магнитной индукции внутри длинного соленоида вдали от его торцов будет одинаковым во всех точках. Для наглядности на рисунках линии индукции изображают гуще в тех местах магнитного поля, где больше значение магнитной индукции (см. рис. 197, б). При этом на линии индукции изображают стрелку в направлении индукции магнитного поля. Для крайних витков соленоида магнитное поле кругового витка с током, проходящим в направлении движения часовой стрелки, эквивалентно полю южного полюса постоянного магнита, а магнитное поле кругового витка с током, проходящим против направления движения часовой стрелки, эквивалентно полю северного полюса постоянного магнита (правило часовой стрелки).

Магнитное поле, индукция которого во всех точках одинакова, называют однородным. Линии индукции такого поля параллельны. В противном случае поле называют неоднородным. Магнитное поле внутри длинного соленоида практически однородно. Вблизи краёв соленоида магнитное поле уже не однородно. Не однородно и магнитное поле прямолинейного проводника с током (см. рис. 192).

Определение направления магнитной индукции

Для определения направления магнитной индукции можно воспользоваться любым из правил, сформулированных выше. Причём, пользуясь правилом буравчика, надо помнить, что направление тока — это направление упорядоченного движения положительных зарядов. Если на рисунке прямолинейный проводник с током изображён не в плоскости страницы, так как расположен перпендикулярно ей (рис. 198), и при этом ток направлен к читателю, то его условно обозначают точкой (рис. 199, а). В случае, если ток направлен от читателя, — крестиком (рис. 199, б). Так же (точка и крестик) обозначают векторы (магнитная индукция, сила и др.), если их направления перпендикулярны плоскости рисунка.

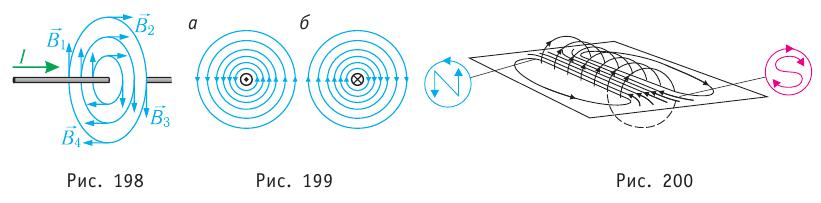
Полюсы соленоида, а следовательно, и направление магнитной индукции, можно определить по правилу часовой стрелки (рис. 200) или правилу буравчика: при вращении рукоятки буравчика по току в витке поступательное движение острия буравчика укажет направление магнитной индукции внутри соленоида, а следовательно, и положение его северного полюса.

1. За направление индукции магнитного поля принимают направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Это направление совпадает с направлением положительной нормали к плоскости небольшой рамки с током, свободно сориентировавшейся в окрестности этой же точки магнитного поля.
2. Линией индукции магнитного поля называют воображаемую линию в магнитном поле, касательная к которой совпадает с направлением индукции магнитного поля в каждой точке.
3. Линии индукции магнитного поля всегда замкнуты и не пересекаются.
4. Магнитное поле, индукция которого во всех точках одинакова, называют однородным.

Пример №1

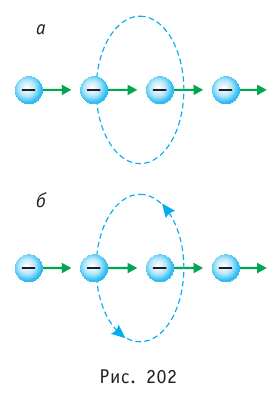
Пучок электронов движется так, как показано на рисунке 202, а. Определите направление линий индукции магнитного поля, образованного этим пучком.

Решение. Определить направление линий индукции магнитного поля, образованного движущимся пучком электронов, можно как по правилу буравчика, так и по правилу правой руки. Однако следует помнить, что эти правила сформулированы для движущихся положительных зарядов. Поэтому в данном случае надо учесть, что за направление электрического тока принято направление, противоположное движению электронов, образующих пучок. Тогда, если смотреть на линию индукции по направлению движения электронов, она будет сориентирована против направления движения часовой стрелки (рис. 202 , б).

Пример №2

На рисунке 203 показано направление электрического тока в соленоиде. Определите магнитные полюсы соленоида.

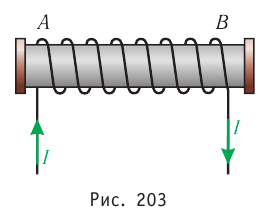
Решение. В данной задаче для определения магнитных полюсов соленоида можно воспользоваться как правилом буравчика, так и правилом часовой стрелки. В первом случае будем мысленно вращать буравчик по направлению тока в витках соленоида. Остриё буравчика при этом перемещается вдоль оси соленоида от торца А к торцу В. Так как линии индукции внутри магнита направлены от южного полюса к его северному полюсу, то по аналогии можно сделать вывод, что у торца А — южный полюс соленоида, а у торца В — северный.

Проверим свой вывод, применив правило часовой стрелки. Если смотреть со стороны торца А соленоида, то видно, что направление тока в витке совпадает с направлением движения часовой стрелки. Следовательно, у торца А — южный полюс, а у торца В — северный.

Закон Ампера. Принцип суперпозиции магнитных полей

Для количественного описания магнитного поля необходимо знать не только направление индукции магнитного поля, но и её модуль. Количественно описать магнитное поле можно, как и электростатическое, на основе его источников, т. е. токов. Для обнаружения магнитного поля и определения его характеристик используют «пробный» ток, который представляет собой малый участок проводника (элемент тока). Определив силу, действующую на каждый элемент тока со стороны магнитного поля, можно вычислить силу, действующую на весь проводник.

Модуль индукции магнитного поля

Действие магнитного поля на находящийся в нём малый участок проводника с током экспериментально исследовал Ампер, проводя опыты с различными проводниками, входящими в замкнутые электрические цепи. В 1820 г. Ампер получил формулу для силы, с которой однородное магнитное поле действует на прямолинейный участок проводника с током.

Постоянный дугообразный магнит закрепим в вертикальной плоскости так, чтобы линии индукции создаваемого им магнитного поля в пространстве между полюсами располагались вертикально (рис. 209). Магнитное поле магнита,

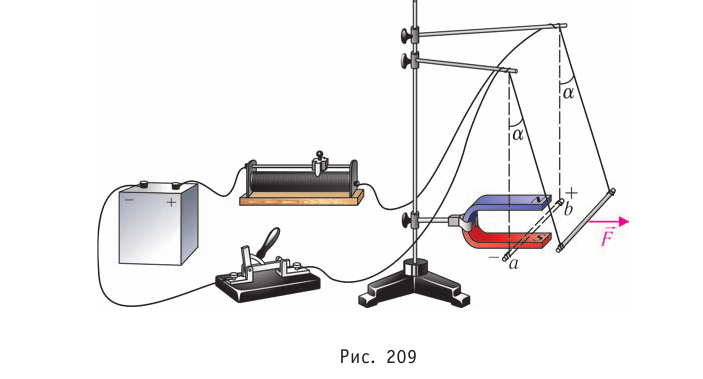
в основном сосредоточенное между его полюсами, будем считать однородным. Именно в этой области поля находится малый (определяемый размерами области пространства, где магнитное поле практически однородно) участок 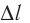прямолинейного проводника длиной 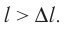Этот проводник подвешен и соединён с источником тока с помощью тонких проводов так, чтобы он располагался перпендикулярно плоскости, в которой находится магнит. Действием слабого магнитного поля на остальные части электрической цепи можно пренебречь.

При замыкании цепи в зависимости от направления электрического тока и расположения полюсов магнита проводник под действием горизонтальной силы 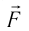начнёт двигаться вправо или влево. При этом подвес отклоняется от вертикального положения на некоторый угол а. Увеличивая силу тока в электрической цепи в 2, 3, 4... раза, можно заметить, что во столько же раз увеличивается и модуль силы F, действующей на проводник (его можно измерить динамометром, отклоняя обесточенный подвес на такой же угол а, или рассчитать по формуле F-mg tga). Добавляя ещё один такой же и так же расположенный магнит для увеличения размеров области, где магнитное поле достаточно велико и практически однородно, можно добиться увеличения длины 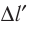прямолинейного участка проводника, находящегося в однородном магнитном поле, 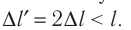Модуль силы, действующей на проводник, при этом увеличивается в 2 раза. Располагая магнит не в вертикальной плоскости, а под углом к поверхности стола, на котором находится установка, можно изменять угол между направлением линий индукции и проводником. Как показывает опыт, модуль силы, с которой магнитное поле действует на проводник с током, прямо пропорционален синусу угла между направлениями тока в проводнике и магнитной индукции. Причём модуль силы достигает максимального значения 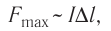когда участок проводника с током образует угол 90° с направлением индукции магнитного поля (sin 90°= 1), и минимален 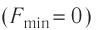в случае расположения проводника параллельно линиям индукции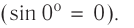

Итак, модуль силы, действующей со стороны однородного магнитного поля на прямолинейный участок проводника с током, пропорционален силе тока I, длине этого участка 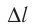и синусу угла а между направлениями тока в проводнике и индукции магнитного поля:

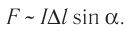
Эта сила названа в честь А. М. Ампера силой Ампера.
Так как 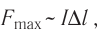 то отношение  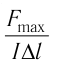для данной области магнитного поля
не зависит ни от силы тока I в проводнике, ни от длины 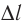прямолинейного участка проводника, полностью находящегося в однородном магнитном поле. Поэтому данное отношение может служить характеристикой той области магнитного поля, в которой находится участок проводника. Это позволяет дать следующее определение индукции магнитного поля.

Индукция магнитного поля — физическая векторная величина, модуль которой равен отношению модуля максимальной силы 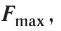действующей со стороны магнитного поля на прямолинейный участок проводника с током, к произведению силы тока I и длины 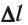этого участка:
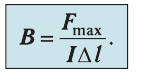(31.1)
Таким образом, в каждой точке магнитного поля может быть определено как направление индукции магнитного поля, так и её модуль.

В СИ индукцию магнитного поля измеряют в теслах (Тл) в честь сербского инженера и изобретателя Никола Тесла (1856—1943), с 1884 г. работавшего в США. 1 Тл — индукция такого однородного магнитного поля, которое на прямолинейный участок проводника длиной 1 м при силе тока в нём 1 А действует максимальной силой, модуль которой 1 Н: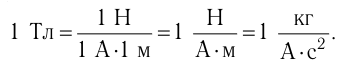

Сила Ампера

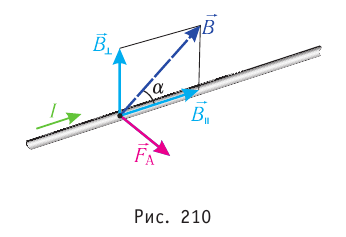
Пусть магнитная индукция составляет угол а с направлением тока в прямолинейном участке проводника длиной 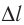 (рис. 210). Если весь прямолинейный проводник длиной l находится в однородном магнитном поле, то 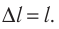Как уже отмечалось, в случае расположения проводника параллельно линиям индукции магнитное поле не оказывает на проводник никакого воздействия. Поэтому модуль силы Ампера зависит лишь от модуля составляющей магнитной индукции 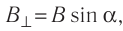перпендикулярной проводнику, и не зависит от модуля составляющей 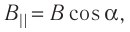параллельной проводнику.

Из выражения (31.1) следует, что модуль максимальной силы Ампера

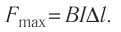
В общем случае модуль силы Ампера можно рассчитать по формуле
(31.2)
Выражение (31.2) называют законом Ампера.

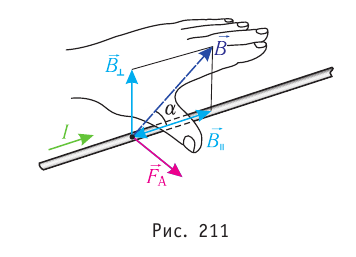
Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая индукции магнитного поля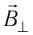 входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° в плоскости ладони большой палец покажет направление силы Ампера, действующей на прямолинейный участок проводника с током (рис. 211).
Закон Ампера позволяет объяснить взаимодействие параллельных проводников с током (рис. 212). Ток силой 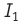создаёт магнитное поле индукцией 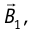действующее 

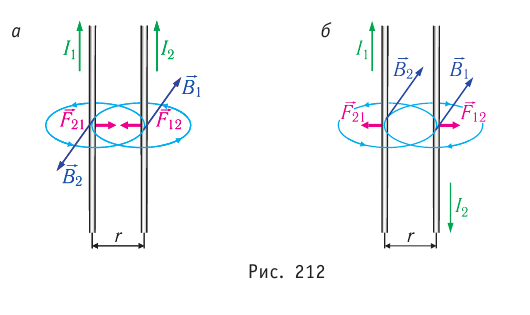
на проводник с током 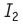силой, модуль которой 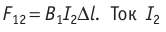создаёт магнитное поле, индукция которого 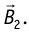Это поле действует на проводник с током 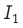силой,

модуль которой 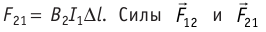находятся в той же плоскости, что и проводники с током, и являются силами притяжения, если токи направлены в одну сторону (рис. 212, а), и силами отталкивания, если токи направлены в противоположные стороны (рис. 212, б) (проверьте это самостоятельно, используя правило буравчика (или правило правой руки) для определения направлений индукций магнитных полей 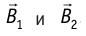и правило левой руки для определения направлений сил Ампера).

Принцип суперпозиции магнитных полей

Когда магнитное поле создаётся несколькими источниками, то индукцию результирующего магнитного поля можно определить по принципу суперпозиции: если магнитное поле в некоторой точке пространства создаётся не одним, а несколькими электрическими токами (или движущимися зарядами), то индукция результирующего магнитного поля в этой точке равна векторной сумме индукций магнитных полей, созданных каждым током (движущимся зарядом):

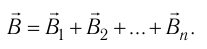    (31.3)

Магнитные поля, созданные различными источниками

Для того чтобы рассчитать индукцию результирующего магнитного поля, используя принцип суперпозиции, необходимо уметь определять индукции магнитных полей, созданных различными источниками. Эксперименты показывают, что во всех случаях модуль индукции магнитного поля, созданного током, пропорционален силе тока, зависит от длины и формы проводника с током и расстояния до выбранной точки. Зависимость индукции магнитного поля прямолинейного проводника с током от расстояния до него экспериментально исследовали французские учёные Жан Батист Био (1774—1862) и Феликс Савар (1791 — 1841) в 1820 г. Французский учёный Пьер Симон Лаплас (1749—1827), проанализировав экспериментальные данные, полученные Био и Саваром, предложил использовать элемент тока (аналог точечного заряда в электростатике), что позволило сформулировать закон, получивший название закона Био — Савара—Лапласа.

Закон, полученный Био, Саваром и Лапласом, позволяет, в частности, рассчитать модуль индукции магнитного поля, созданного постоянным током

силой l проходящим по круговому витку (находящемуся в вакууме или воздухе) радиусом R, в центре этого витка по формуле

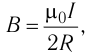
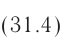
где 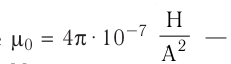магнитная постоянная.

Модуль индукции магнитного поля, созданного постоянным током силой l, который проходит по бесконечно длинному прямолинейному проводнику (находящемуся в вакууме или воздухе), в точках, расположенных на расстоянии r от оси проводника, определяют по формуле

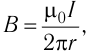
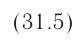
которая соответствует результатам экспериментов, проведённых Био и Саваром.

Модуль индукции магнитного поля, созданного постоянным током силой I, внутри длинного соленоида, находящегося в вакууме или воздухе, можно определить по формуле

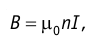
где 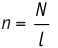 число витков на единицу длины соленоида.

Пусть расстояние между тонкими длинными параллельными прямолинейными проводниками с током r (см. рис. 212). Тогда модуль индукции магнитного поля, созданного током силой 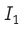первого проводника в тех точках пространства, где находится
второй проводник,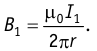

Соответственно модуль индукции магнитного поля тока
силой 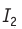второго проводника в тех точках пространства, где размещён первый проводник,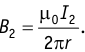

Поэтому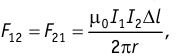т. е. силы взаимодействия параллельных проводников с током подчиняются третьему закону Ньютона.

Отметим, что взаимодействие отдельных элементов тока не подчиняется третьему закону Ньютона, потому что магнитные силы 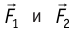2 в общем случае не лежат на одной прямой. Однако для сил взаимодействия замкнутых контуров, состоящих из проводников с токами, третий закон Ньютона выполняется, т. е.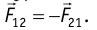

1. Индукция магнитного поля — физическая векторная величина, модуль которой равен отношению модуля максимальной силы, действующей со стороны магнитного поля на прямолинейный участок проводника с током, к произведению силы тока и длины этого участка:

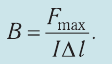
2.    1 Тл — магнитная индукция такого однородного магнитного поля, которое на прямолинейный участок проводника длиной 1 м при силе тока в нём 1 А действует максимальной силой, модуль которой 1 Н: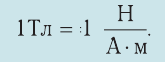

3.    Модуль силы Ампера можно рассчитать по формуле

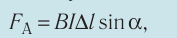
где а — угол между направлениями тока и индукции магнитного поля.

4.    Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая индукции магнитного поля 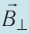входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° в плоскости ладони большой палец покажет направление силы Ампера, действующей на участок проводника с током.

5.    Если магнитное поле в некоторой точке пространства создаётся не одним, а несколькими электрическими токами (или движущимися зарядами), то индукция результирующего магнитного поля в этой точке равна векторной сумме индукций магнитных полей, созданных каждым током (или движущимся зарядом) (принцип суперпозиции)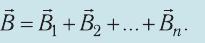

Пример №3

В однородном магнитном поле, индукция которого направлена вертикально и её модуль B = 0,50 Тл, на лёгких проводах горизонтально подвешен прямолинейный металлический стержень длиной l = 0,20 м и массой т = 50 г. Определите, на какой угол от вертикали отклонятся провода, поддерживающие стержень, если по нему пропустить ток силойm= 5,0 А. Воздействием магнитного поля на ток в подводящих проводах пренебречь.
Дано:

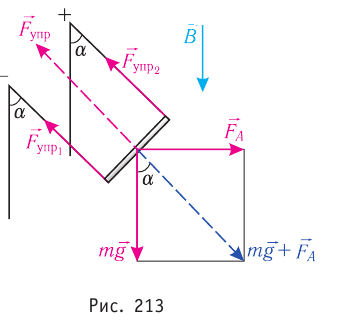
Решение. На стержень действуют силы упругости проводов 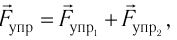сила тяжести 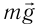и сила Ампера 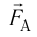(рис. 213). Модуль этой силы определяют по закону Ампера:  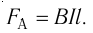   При равновесии стержня

векторная сумма сил равна нулю: 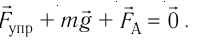Из рисунка 213 следует:

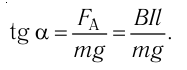
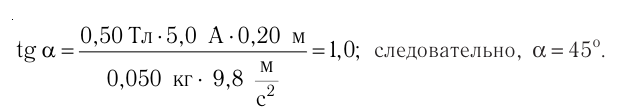
Ответ: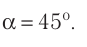

Пример №4

По двум одинаковым круговым виткам радиусом 6 = 6,28 см каждый, плоскости которых взаимно перпендикулярны, а центры совпадают,проходят одинаковые токи силой l =4,0 А. Определите модуль индукции магнитного поля в центре витков. Витки находятся в воздухе.
Дано:

Решение. Модуль индукции магнитного поля, созданного каждым круговым током в центре соответствующего витка, найдём по формуле (31.4)

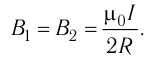
По правилу буравчика для выбранных направлений токов в витках индукция 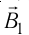направлена перпендикулярно плоскости рисунка от нас, а индукция 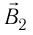— вправо (рис. 214). Согласно принципу суперпозиции (31.3) индукция результирующего магнитного поля 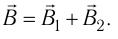Так как индукции магнитных полей взаимно перпендикулярны, по теореме Пифагора находим: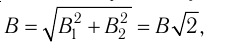

тогда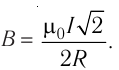

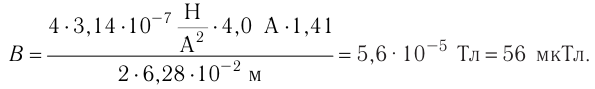
Ответ: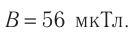

Сила Лоренца

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих движущихся заряженных частиц. Таким образом, силу Ампера, модуль которой 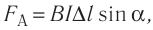можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Силу, с которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося голландского физика Хендрика Антона Лоренца (1853—1928).
 

Модуль силы Лоренца можно определить по формуле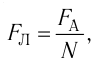
где N — общее число свободных заряженных частиц на прямолинейном участке проводника длиной 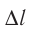(рис. 217). Если модуль заряда одной частицы q, а модуль суммарного заряда всех частиц 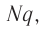то согласно определению силы тока  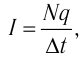где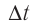 промежуток времени, за который заряженная частица проходит участок проводника длиной 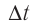. Тогда

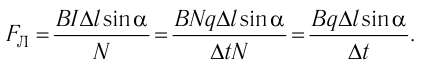
Поскольку 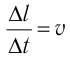— модуль средней скорости заряженной частицы, упорядоченно движущейся в магнитном поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде

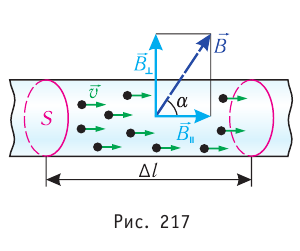
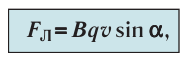(32.1)
где a — угол между направлениями индукции магнитного поля 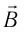и скорости 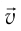упорядоченного движения заряженной частицы.

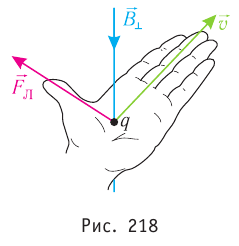
Направление силы Лоренца, действующей на заряженные частицы, как и силы Ампера, определяют по правилу левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости упорядоченного движения заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° в плоскости ладони большой палец покажет направление действующей на заряд силы Лоренца (рис. 218).

Отметим, что сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряда может отличаться.

Движение заряженных частиц в однородном магнитном поле

Под действием силы Лоренца частицы, имеющие электрический заряд, движутся в магнитном поле по криволинейным траекториям. Причём если в данной инерциальной системе отсчёта направление скорости движения частицы перпендикулярно направлению индукции магнитного поля 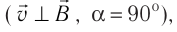то траекторией движения заряженной частицы в однородном магнитном поле является окружность (рис. 219). Пусть частица массой m и зарядом q движется со скоростью 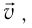направленной перпендикулярно линиям индукции в однородном магнитном поле, индукция которого 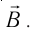Так как сила Лоренца 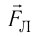перпендикулярна скорости 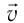движения частицы (см. рис. 219), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона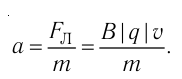

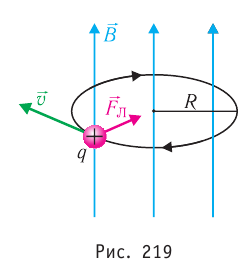
В результате частица движется по окружности, радиус которой можно
определить из формулы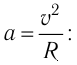
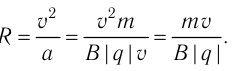(32.2)
 

Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:

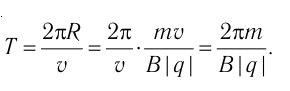
Как видно из выражения (32.3), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только параметрами частицы (модулем её заряда и массой) и величиной магнитной индукции. Это используют в циклических ускорителях заряженных частиц — циклотронах.

На частицу, движущуюся вдоль линии индукции магнитного поля, сила Лоренца не действует (sin a = 0).

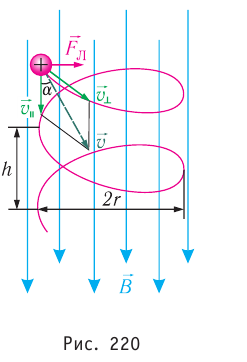
 Если заряженная частица движется в однородном магнитном поле так, что направление её скорости 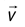образует с индукцией магнитного поля 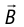угол а, причем 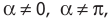то траектория движения частицы представляет собой винтовую линию (рис. 220). При этом радиус R винтовой линии зависит от модуля составляющей скорости 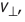перпендикулярной индукции магнитного поля, а шаг винтовой линии h — от модуля составляющей скорости 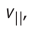параллельной магнитной индукции. Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции.

Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 221), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за время порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 222).

Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 223), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю.

Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц. Увеличение кинетической энергии частицы, т. е. её ускорение, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе сил поля). Поэтому в современных ускорителях заряженных частиц электрическое поле используют для ускорения, а магнитное— для «формирования» траектории движения заряженных частиц.
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, 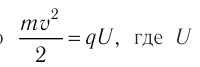— напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля

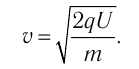(32.4)
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна её скорости, то радиус окружности, по дуге которой будет двигаться частица, 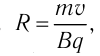 откуда

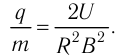
Величину 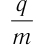называют удельным зарядом частицы. Поэтому, если опытным путём определить радиус траектории частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс-спектрометрами.
 

1. Силу, с которой магнитное поле действует на заряд, движущийся в этом поле, называют силой Лоренца. Модуль силы Лоренца определяют по формуле

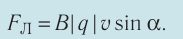
2.    Направление силы Лоренца определяют по правилу левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости движения заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° в плоскости ладони большой палец покажет направление действующей на заряд силы Лоренца.

3.    Работа силы Лоренца при движении заряженной частицы в не изменяющемся во времени магнитном поле равна нулю.

4.    Если в данной инерциальной системе отсчёта скорость движения заряженной частицы перпендикулярна индукции магнитного поля 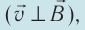, то траекторией движения частицы в однородном магнитном поле является окружность. Период обращения частицы не зависит от скорости её движения и радиуса траектории.

Пример №5

Электрон движется в однородном магнитном поле по окружности радиусом R = 12 см со скоростью, модуль которой значительно меньше модуля скорости света. Определите модуль импульса электрона, если модуль индукции магнитного поля B= 0,020 Тл.

Дано:

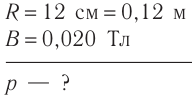
Решение. Модуль импульса электрона p-mv, где т — масса электрона, v — модуль скорости его движения. На электрон в магнитном поле действуют сила Лоренца и сила тяжести, модуль которой во много раз меньше модуля силы Лоренца. Поэтому действием силы  тяжести на движущуюся в магнитном поле заряженную частицу можно пренебречь. Согласно второму закону Ньютона 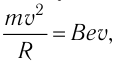откуда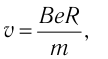

где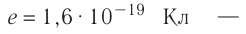

 модуль зарядаэлектрона. Следовательно,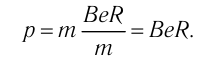

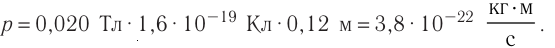
Ответ: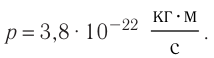

Пример №6

Электрон, ускоренный из состояния покоя в электростатическом поле разностью потенциалов U= 270 В, движется параллельно тонкому длинному прямолинейному проводнику, находящемуся в вакууме, на расстоянии г=5,0 мм от него. Определите модуль силы, которая начнёт действовать на электрон, если по проводнику пустить электрический ток силой l= 10 А, а также радиус кривизны его траектории в начале искривлённого участка. Масса электрона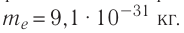

Дано:

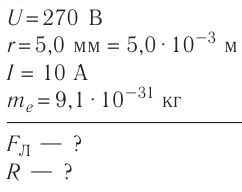
Решение. При разгоне электрона 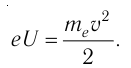Отсюда модуль скорости, до которой разогнали электрон, 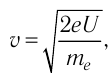где е — модуль заряда электрона. Равномерное прямолинейное движение электрона параллельно тонкому длинному прямолинейному проводнику сменилось равномерным криволинейным, как только по проводнику начал проходить электрический ток и на электрон подействовала сила Лоренца, модуль которой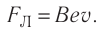

Модуль индукции магнитного поля, образованного тонким длинным прямолинейным проводником с током,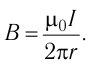
Тогда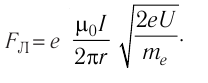

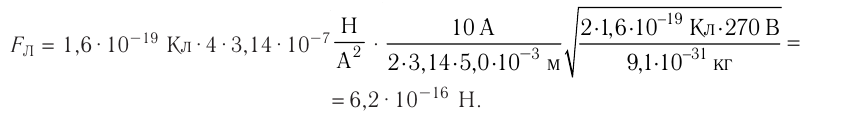
Как только появляется магнитное поле, создаваемое проводником с током, электрон продолжает двигаться, но уже с центростремительным ускорением:

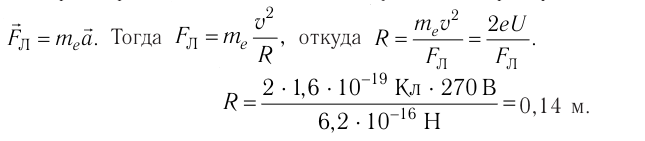
Ответ: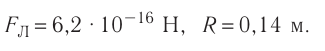

Магнитный поток. Явление электромагнитной индукции. Правило Ленца

После опытов Эрстеда и Ампера стало понятно, что электрические и магнитные поля имеют одни и те же источники — движущиеся электрические заряды. Это позволило предположить, что они каким-то образом связаны друг с другом. Фарадей был абсолютно уверен в единстве электрических и магнитных явлений. Вскоре после открытия Эрстеда в своём дневнике в декабре 1821 г. он записал: «Превратить магнетизм в электричество». На решение этой фундаментальной задачи ему понадобилось десять лет. После многочисленных экспериментов Фарадей сделал эпохальное открытие: замыкая и размыкая электрическую цепь одной катушки, он в замкнутой цепи другой катушки получил электрический ток. Наблюдаемое явление Фарадей назвал электромагнитной индукцией.

Индукция магнитного поля характеризует магнитное поле в конкретной точке пространства. Чтобы охарактеризовать магнитное поле во всех точках поверхности, ограниченной замкнутым контуром, вводят физическую величину, которую называют магнитным потоком (потоком магнитной индукции).

Магнитным потоком Ф через плоскую поверхность, находящуюся в однородном магнитном поле, называют физическую скалярную величину, равную произведению модуля индукции В магнитного поля, площади S поверхности

и косинуса угла а между направлениями нормали к этой поверхности и магнитной индукции (рис. 226):
(33.1
За единицу магнитного потока в СИ принят вебер (Вб).

1 Вб — магнитный поток однородного магнитного поля индукцией 1 Тл через плоскую поверхность площадью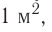расположенную перпендикулярно индукции магнитного поля.

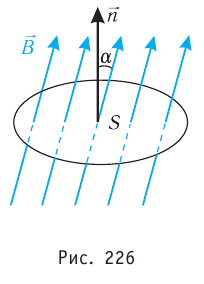
Из формулы (33.1) видно, что магнитный поток зависит от взаимной ориентации линий магнитной индукции и нормали к плоской поверхности. Поток максимален, если ос = 0, т. е. если поверхность перпендикулярна линиям индукции магнитного поля:

Если плоская поверхность параллельна линиям индукции (а = 90°), то поток через неё равен нулю.

На практике часто встречаются ситуации, когда линии магнитной индукции пересекают поверхности, ограниченные не одним контуром, а несколькими. Так, например, линии магнитной индукции могут пересекать поверхности, ограниченные витками соленоида, которые «параллельны» друг другу и имеют одинаковую площадь поверхности. В этом случае магнитный поток определяют по формуле

Ф = NBS,

где N — число витков соленоида, S — площадь поверхности, ограниченной каждым витком.

Изменить магнитный поток через поверхность, ограниченную контуром, можно, изменяя: 1)индукцию магнитного поля, в котором находится контур; 2) размеры этого контура; 3) ориентацию контура в магнитном поле.

Явление электромагнитной индукции

В 1831 г. Фарадей провёл серию опытов, которые позволили установить следующие факты:

— при движении постоянного магнита относительно катушки, подключённой к гальванометру, в катушке возникал электрический ток (стрелка гальванометра отклонялась). Причём направление тока изменялось на противоположное при изменении направления движения магнита. Это же явление наблюдалось, если магнит был неподвижен, а двигали катушку (рис. 227);

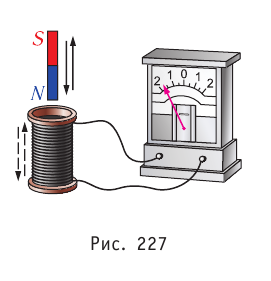
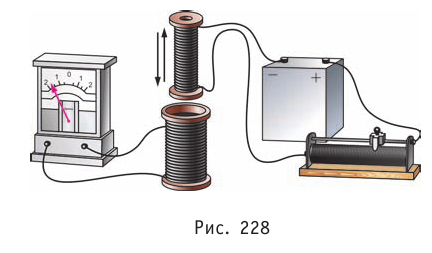
• —    в катушке, подключённой к гальванометру, возникал электрический ток, если относительно неё двигали другую катушку, которая была подключена к источнику постоянного тока (рис. 228);
• —    если две катушки намотаны на общий каркас и одну подключали к гальванометру, а другую — к источнику тока, то ток в первой катушке возникал при изменении тока во второй (рис. 229).

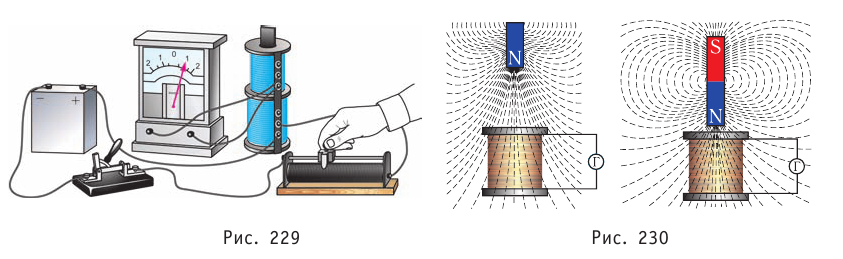
Во всех рассмотренных случаях электрический ток в цепи гальванометра возникал только при изменении магнитного потока через поверхности, ограниченные витками катушки, подключённой к гальванометру (рис. 230). Причём значение силы тока, возникающего в контуре, не зависело от способа изменения магнитного потока, а определялось только скоростью его изменения.

Электрический ток, возникающий в замкнутом проводящем контуре при любом изменении магнитного потока через поверхность, ограниченную этим контуром, называют индукционным током.

Как вы уже знаете, для существования тока в замкнутой электрической цепи необходимо, чтобы на свободные заряженные частицы действовали сторонние силы, т. е. в цепи должен быть источник ЭДС. Очевидно, что в опытах Фарадея источником этих сторонних сил являлся изменяющийся магнитный поток, который создавал в цепи ЭДС. Эту ЭДС называют электродвижущей силой индукции или ЭДС индукции. Если цепь замкнута, ЭДС индукции создаёт индукционный ток, т. е. возникновение индукционного тока является вторичным эффектом.

Явление возникновения ЭДС индукции в контуре, который либо покоится в изменяющемся во времени магнитном поле, либо движется в постоянном магнитном поле так, что магнитный поток через поверхность, ограниченную контуром, меняется, называют электромагнитной индукцией.

Направление индукционного тока

Опыты Фарадея показали, что направление индукционного тока, вызванного возрастанием магнитного потока, было противоположно направлению индукционного тока, вызванного его уменьшением. Исследовав явление электромагнитной индукции, петербургский академик Эмилий Христианович Ленц (1804—1865) в 1833 г. сформулировал правило для определения направления индукционного тока. Согласно этому правилу возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, противодействует изменению магнитного потока, которым вызывается этот индукционный ток. Это означает, что при возрастании магнитного потока магнитное поле индукционного тока направлено против внешнего поля, а при убывании — магнитное поле индукционного тока направлено так же, как и внешнее поле.

В более сжатой форме правило Ленца можно сформулировать следующим образом: индукционный ток всегда направлен так, что его действие противоположно действию причины, вызвавшей этот ток.

Правило Ленца можно проиллюстрировать, используя два алюминиевых кольца (одно из них с разрезом), закреплённых на стержне, свободно вращающемся вокруг вертикальной оси (рис. 231). Опыт показывает, что при приближении постоянного магнита к сплошному кольцу оно отталкивается от магнита; при удалении магнита кольцо притягивается к нему. Отталкивание и притяжение сплошного кольца объясняют возникновением в нём индукционного тока при изменении магнитного потока через поверхность, ограниченную кольцом. Очевидно, что при приближении магнита к кольцу направление индукционного тока таково, что индукция магнитного поля тока противоположна индукции магнитного поля постоянного магнита (рис. 232). При удалении магнита индукции магнитных полей тока и магнита совпадают по направлению.

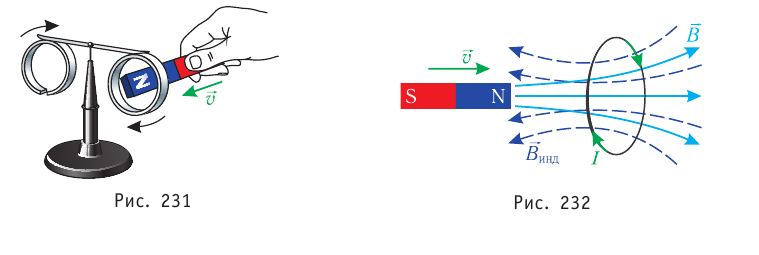
При движении магнита относительно кольца с разрезом взаимодействие не наблюдается, так как индукционный ток отсутствует.

Чтобы определить направление индукционного тока по правилу Ленца, необходимо выполнить следующие операции:

1. определить направление линий индукции внешнего магнитного поля
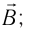
2. выяснить, увеличивается или уменьшается магнитный поток через поверхность, ограниченную проводящим контуром;
3. определить направление линий индукции магнитного поля индукционного тока 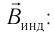: если изменение магнитного потока 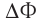< 0, то направления индукций внешнего магнитного поля 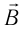и магнитного поля индукционного тока Винд совпадают, если ДФ > 0, то направления противоположны;
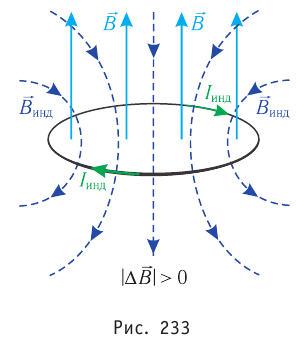
4. зная направление линий индукции магнитного поля индукционного тока 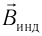по правилу буравчика (правилу часовой стрелки) определить направление индукционного тока (рис. 233).

Правило Ленца соответствует закону сохранения энергии применительно к явлению электромагнитной индукции. В самом деле, если бы индукционный ток имел другое направление, он мог бы существовать без затрат энергии, что противоречит закону сохранения энергии.

Открытие явления электромагнитной индукции имело большое значение. Была доказана взаимосвязь магнитных и электрических явлений, что послужило в дальнейшем отправным пунктом для разработки теории электромагнитного поля.
 

1. Магнитным потоком через плоскую поверхность называют физическую скалярную величину, равную произведению модуля индукции однородного магнитного ноля, площади поверхности и косинуса угла между направлениями магнитной индукции и нормали к этой поверхности: Ф = BScos a.
2. Явление возникновения ЭДС индукции в контуре, который либо покоится в изменяющемся во времени магнитном поле, либо движется в постоянном магнитном поле так, что число линий магнитной индукции, пронизывающих контур, меняется, называют электромагнитной индукцией.
3. Электрический ток, возникающий в замкнутом проводящем контуре при любом изменении магнитного потока через поверхность, ограниченную этим контуром, называют индукционным током.
4. Возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, противодействует изменению магнитного потока, которым вызывается этот индукционный ток (правило Ленца).

Закон электромагнитной индукции

Открыв явление электромагнитной индукции, Фарадей практически за полтора месяца установил все существенные закономерности этого явления. Ему стала понятна сущность явления, которое сыграло такую важную роль для человечества: во всех экспериментах, проведённых им, индукционный ток в проводящем контуре возникал в результате изменения магнитного потока через поверхность,

ограниченную этим контуром. Фарадей не только открыл явление электромагнитной индукции, но и первым продемонстрировал, «что можно создать постоянный ток электричества при помощи обыкновенных магнитов», сконструировав униполярный генератор электрического тока, превращающий механическую энергию в электрическую.

Анализируя результаты опытов Фарадея, Максвелл в 1873 г. пришёл к выводу, что ЭДС индукции в замкнутом проводящем контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром, т. е.

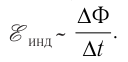   (34.1)
Чтобы обеспечить строгое равенство в выражении (34.1), необходимо учесть направление индукционного тока. Согласно правилу Ленца при увеличении

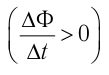ЭДС индукции отрицательная 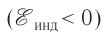и,
наоборот, при уменьшении магнитного потока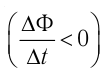 ЭДС индукции положительная  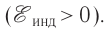Тогда
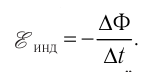 (34.2)

Таким образом, ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком.

Выражение (34.2) называют законом электромагнитной индукции Фарадея, подчёркивая этим заслуги учёного в изучении указанного явления. Следует отметить, что данный закон является универсальным, т. е. ЭДС индукции не зависит от способа изменения магнитного потока.

Согласно закону Ома для полной цепи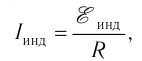

где R — сопротивление проводника, из которого изготовлен замкнутый проводящий контур.

Вихревое электрическое поле

Итак, при изменении магнитного потока через поверхность, ограниченную проводящим контуром, в замкнутом неподвижном (относительно выбранной инерциальной системы отсчёта) контуре возникает электрический ток. Это свидетельствует о том, что на свободные

заряженные частицы в контуре действуют силы. Но для хаотически движущихся заряженных частиц усреднённое значение силы Лоренца равно нулю, поэтому на такие частицы действие оказывает электрическое поле. Таким образом, при любом изменении магнитного поля в окружающем пространстве возникает электрическое поле. Именно это индукционное электрическое поле действует на заряженные частицы, приводя их в упорядоченное движение и создавая индукционный электрический ток. Подчеркнём, что индукционное электрическое поле не связано с электрическими зарядами, его источником является изменяющееся со временем магнитное поле. Линии напряжённости индукционного электрического поля замкнуты.

Электрическое поле, возникающее при любом изменении магнитного поля, называют вихревым электрическим полем.

Вихревой, т. е. непотенциальный, характер индукционного электрического поля является причиной того, что при перемещении заряда по замкнутой цепи силами этого поля совершается работа, не равная нулю.

Таким образом, ЭДС индукции, которая возникает в неподвижном замкнутом контуре, находящемся в изменяющемся магнитном поле, равна работе сил вихревого электрического поля по перемещению вдоль этого контура единичного положительного заряда. Если такой контур оказывается проводящим, то возникшая в нём ЭДС индукции приводит к появлению индукционного тока.

Максвелл в 1873 г. установил, что ЭДС индукции, возникающая в неподвижном контуре при изменении магнитного поля, не зависит от характеристик этого контура (вещества, вида свободных носителей заряда, сопротивления, температуры и др.). На основании этого он сделал вывод, что роль контура сводится только к индикации вихревого электрического поля, создаваемого переменным магнитным полем.

Итак, сущность явления электромагнитной индукции заключается в том, что вихревое электрическое поле возникает в любой точке пространства, если в этой точке существует изменяющееся магнитное поле, независимо от того, есть там проводящий контур или нет.

Линии напряжённости вихревого электрического поля охватывают линии индукции изменяющегося магнитного поля. Направление линий напряжённости вихревого электрического поля определяется по правилу Ленца. Действительно, если поместить в изменяющееся магнитное поле замкнутый проводящий контур, то по нему в направлении линий напряжённости электрического поля пойдёт индукционный электрический ток.

Этот ток создаёт индукционное магнитное поле, индукция которого 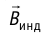показана на рисунке 235 штриховыми линиями. Она направлена так, что индукционное поле противодействует изменению основного магнитного поля (правило Ленца): если модуль индукции основного поля возрастает, то 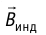противоположна индукции основного поля 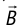(рис. 235,а); если модуль индукции основного поля уменьшается, то 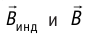имеют одинаковое направление (рис. 235, б).

ЭДС индукции возникает не только в контуре, находящемся в состоянии покоя относительно определённой инерциальной системы отсчёта, при изменении магнитного потока через поверхность, ограниченную контуром, но и при движении проводника в постоянном магнитном поле. ЭДС индукции, возникающая в прямолинейном проводнике, поступательно движущемся в однородном магнитном поле, прямо пропорциональна модулю индукции магнитного поля В, длине активной части проводника l(части, которая находится в магнитном поле), модулю поперечной скорости движения проводника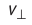 и синусу угла а между направлениями магнитной индукции поля 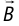и поперечной скорости движения проводника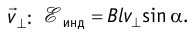

• ЭДС индукции в контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком (закон электромагнитной индукции Фарадея): 
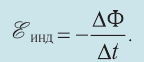
• Электрическое поле, возникающее при любом изменении магнитного поля, называют вихревым электрическим полем.
• Вихревое электрическое поле возникает в любой точке пространства, если в этой точке существует изменяющееся со временем магнитное поле, независимо от того, есть там проводящий контур или нет. •

Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током

Электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797—1878) независимо от своего английского коллеги открыл некоторые из элек-

гиромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Оказалось, что изменяющийся электрический ток, проходящий в контуре, создаёт изменяющийся магнитный поток. Это явление было названо самоиндукцией.

Самоиндукция

Самоиндукция является важным частным случаем явления электромагнитной индукции. Если электрический ток в замкнутом проводящем контуре по каким-либо причинам изменяется, то изменяется и магнитное поле этого тока (В ~ I). Но при изменении индукции магнитного поля, создаваемого током, проходящим в контуре, изменяется и магнитный поток (Ф ~ В). Следовательно, магнитный поток через поверхность, ограниченную контуром, пропорционален силе тока в контуре:

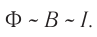
Коэффициент пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил назвать «коэффициент самоиндукции»:

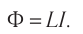   (35.1)

Коэффициент самоиндукции L часто называют индуктивностью контура.

Индуктивность в СИ измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.

Например, индуктивность однослойного соленоида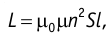 где n — число витков на единицу длины соленоида, S — площадь поверхности, ограниченной витком, l — длина соленоида, 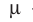— магнитная проницаемость среды. Увеличить магнитную проницаемость среды можно введением в соленоид ферромагнитного сердечника.

Из формулы (35.1) следует, что изменить магнитный поток можно, изменяя силу тока в контуре, или его индуктивность, или то и другое одновременно. Согласно закону электромагнитной индукции изменяющийся магнитный поток создаёт в контуре ЭДС, которую в этом случае называют электродвижущей силой самоиндукции или ЭДС самоиндукции:

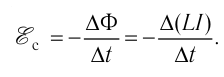
Если индуктивность контура не изменяется во времени, т. е. L = const, то

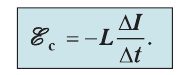
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции, силу которого определяют но закону Ома 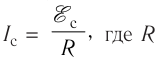— сопротивление контура. Согласно правилу Ленца ток самоиндукции всегда направлен так, что он противодействует изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.

Наблюдение самоиндукции

Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока (рис. 238). При замыкании цепи лампочка 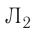начинает светиться практически сразу, лампочка 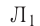— с заметным запаздыванием. При возрастании силы тока 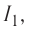созданного источником, на участке, образованном катушкой и лампочкой 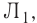ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции 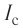направлен навстречу току источника. В результате рост силы тока на этом участке цепи замедляется, и сила тока 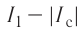не сразу достигает своего максимального значения.

Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки 1 с большим количеством витков, намотанных на железном сердечнике 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 239). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.

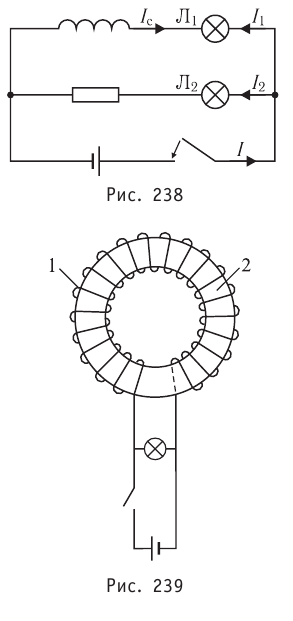
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их со-
противлений 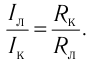Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.

Энергия магнитного поля

Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.

В самом деле, при замыкании цепи, состоящей из источника тока с ЭДС 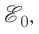катушки индуктивностью L и резистора сопротивлением R, сила тока /
в цепи начнёт возрастать и появится ЭДС самоиндукции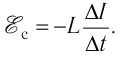  

Тогда в соответствии с законом Ома сила тока в цепи 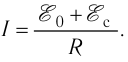Значит

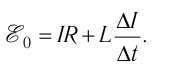
Умножив полученное равенство на 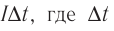— достаточно малый промежуток времени, в течение которого сила тока остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: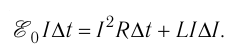

В процессе установления тока, когда сила тока / и магнитный поток Ф = 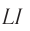возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся на резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени 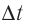при преодолении ЭДС самоиндукции в процессе установления тока (рис. 240):

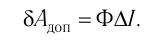
Полная дополнительные работа 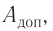равная сумме элементарных дополнительных работ 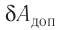в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(l) (рис. 240):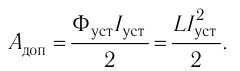

Эта работа превращается в энергию магнитного поля катушки, поэтому

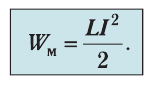
 1. Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи называют самоиндукцией.

2.    ЭДС самоиндукции равна произведению индуктивности контура (катушки) и скорости изменения силы тока в нём, взятому с противоположным знаком: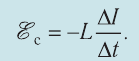

3.    Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

4.    Энергия магнитного поля катушки с током прямо пропорциональна квадрату силы тока:

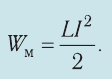
Пример №7

За промежуток времени 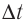= 9,50 мс сила тока в катушке индуктивности равномерно возросла от 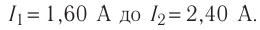При этом в катушке возникла ЭДС самоиндукции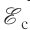= —14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.

Дано:

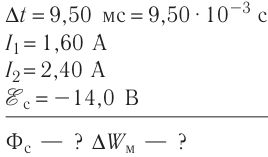
Решение. При изменении в катушке силы тока от 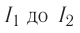возникает собственный магнитный поток, 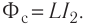Индуктивность L катушки можно определить из закона электромагнитной индукции

для явления самоиндукции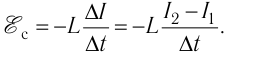 

Следовательно,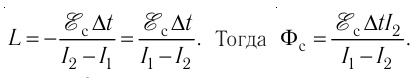

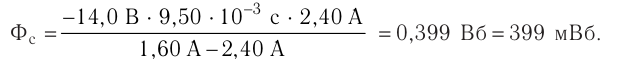
Приращение энергии магнитного поля катушки

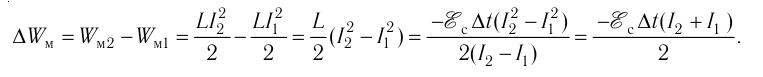
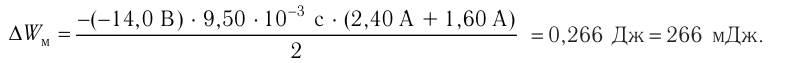
Ответ: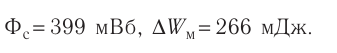

Явление электромагнитной индукции

В 1820 году, после открытия магнитного действия тока ученым из Дании - Г. Эрстедом, английский ученый Майкл Фарадей поставил перед собой цель: создать электрический ток с помощью магнитного поля. Работая над этим в течение 10 лет, в 1831 году он сумел решить эту задачу

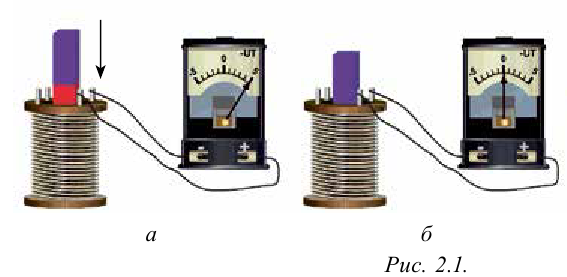
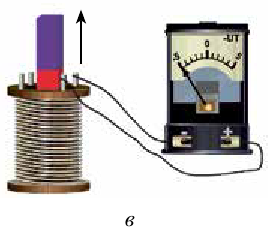
Рассмотрим эксперименты, проведенные Фарадеем с помощью демонстрационных устройств. Соединяя последовательно катушку и гальванометр, он создал замкнутую цепь (рис. 2.1). При вводе постоянного магнита в катушку наблюдается отклонение стрелки гальванометра. При этом в катушке появляется электрический ток (рис. 2.1 а). Если магнит находится в катушке без движения, то стрелка гальванометра показывает ноль, т.е. наблюдается исчезновение электрического тока в катушке (рис. 2.1 б). При извлечении магнита из катушки снова наблюдается появление тока в катушке. Тогда стрелка гальванометра отклоняется в другую сторону (рис. 2.1 в). Если магнит неподвижен, а катушку приводим в движение, опять наблюдается появление тока. Значит, в случае любого изменения магнитного потока, пронизывающего катушку, в ней появляется электродвижущая сила.

Если концы проволочной рамки соединены между собой напрямую (или через какой-либо прибор), его можно назвать замкнутым контуром. В этом случае катушка, соединенная с гальванометром, образует замкнутый контур, соединенный последовательно.

Появление электрического тока в замкнутом контуре в результате изменения потока магнитного поля называется явлением электромагнитной индукции, а электрический ток, который появляется в контуре, называется индукционным током.

Фарадей, делая анализ результатов, полученных в результате экспериментов, пришел к выводу: индукционный ток появляется только в случае изменения потока магнитной индукции, проходящего через контур проводника, т.е. существует только в момент изменения потока магнитной индукции.

Известно, что для существования тока в электрической цепи продолжительное время должен быть источник электродвижущей силы (ЭДС) в какой-либо части цепи. ЭДС, которая появляется в результате непрерывного изменения магнитного потока в контуре, служит как внешний источник для появления в нем индукционного тока. ЭДС, создающая индукционный ток, называется индукционной электродвижущей силой.

Количественное значение ЭДС, возникающей в закинутом контуре, определяет закон электромагнитной индукции. По этому закону ЭДС индукции равна скорости изменения магнитного потока, пронизывающего контур, и противоположна ему по знаку:

Это называется законом электромагнитной индукции, или законом Фарадея-Максвелла.

Знак (-) в выражении (2-1) связан с направлением индукционного тока, возникающем в контуре, и это объясняется правилом Ленца.В системе СИ единицей измерения индукционной электродвижущей силы принято обозначать как вольт (В).

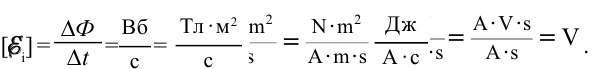
Если контур состоит их N витков, индукционная ЭДС, которая появилась в контуре, вычисляется с помощью следующего выражения:

Для определения направления индукционного тока русский ученый X. Ленц провел следующий эксперимент. Он взял два легких кольца из алюминия, одно целое, а второе с прорезью, и подвесил их на веревку (рис. 2.2). Если приближать магнит к целому кольцу, в нем появляется индукционный ток. В то же время этот ток внутри кольца создает свое магнитное поле. Созданное магнитное поле препятствует приближению магнита к кольцу и кольцо отталкивается от магнита (рис. 2.2 а). Если удалять магнит от кольца, то кольцо притягивается к магниту.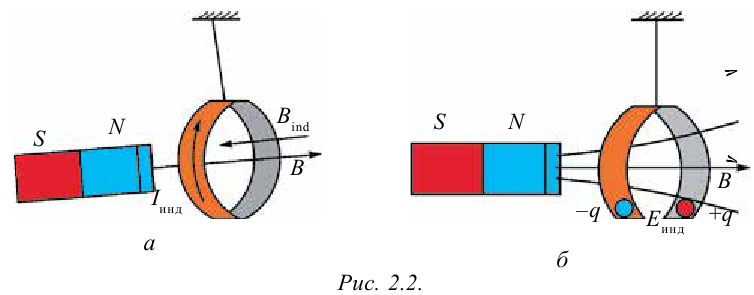

В случае приближения магнита к кольцу с прорезью или при удалении магнита от него действия магнита на кольцо не наблюдается. Причиной этого является отсутствие индукционного тока в кольце из-за того, что контур не замкнут (рис. 2.2 в). По результатам экспериментов, Ленц вывел правило определения направления индукционного тока. Это правило в его честь названо правилом Ленца: индукционный ток в замкнутом контуре направлен так, что создаваемый им поток магнитной индукции стремится препятствовать тому изменению потока, которое порождает данный ток.

Пример №8

Магнитный поток, проходящий через кольцо из проводника в течение 0,2 с, изменен на 5 мВб. Какой индукционный ток появится в кольце, если кольцо имеет сопротивление, равное 0,25 Ом?

Дано: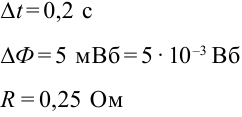    Найти: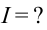

Формула: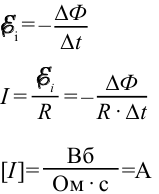

Решение: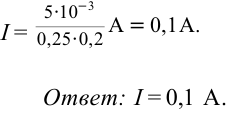

ЭДС самоиндукции

Ток, проходящий через любой контур, создает магнитный поток, пронизывающий этот контур. Если изменится ток, проходящий по контуру, изменится и создаваемый им магнитный поток. В результате в контуре появится ЭДС индукции. Это явление называется явлением самоиндукции.

Электрическая цепь, в которой можно наблюдать явление самоиндукции, приведена на рис. 2.3 а. Цепь состоит из двух одинаковых ламп, сопротивления R, катушки с большим количеством витков, ключа и источника тока. К источнику тока одна из ламп подсоединена через катушку с металлическим сердечником внутри, а вторая лампа - через сопротивление R.

При замыкании ключа лампа, подсоединенная через катушку, зажигается с опозданием, а вторая лампа, подсоединенная через сопротивление R, зажигается сразу после соединения (рис. 2.3 б). Это происходит потому, что при замыкании ключа сила тока, протекающая через катушку за время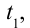 изменяется от нуля до 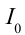(рис. 2.3 в).

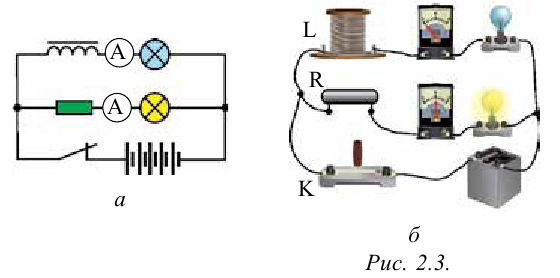
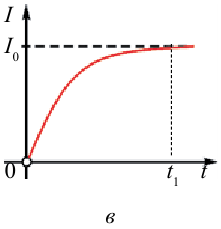
За это время в катушке возникает ток самоиндукции, направленный против тока, образованного источником тока. Поэтому первая лампа загорается с опозданием.

За счет самоиндукции при размыкании ключа (отключение тока) вторая лампа отключается сразу, а первая лампа гаснет постепенно.

Магнитное поле, образованное током, описывается магнитным потоком. От каких физических величин зависит магнитный поток, образованный внутри катушки?

Как показывают эксперименты, магнитный поток, образованный внутри катушки: во-первых, прямо пропорционален силе тока, проходящего по ней, т.е.:

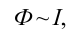
во-вторых, зависит от геометрических размеров катушки (количества витков, поперечного сечения, длины) и наличия сердечника.

Обобщая результаты этих экспериментов, приходим к следующему выводу: магнитный поток, образованный проводником с током, зависит от силы тока, протекающего по нему, и параметров катушки, т.е.:

здесь: L - коэффициент пропорциональности, зависящий от геометрических размеров катушки, магнитных свойств среды, где расположена катушка, который называется индуктивностью катушки.

В системе СИ единицей измерения индуктивности в чссть американского ученого Дж. Генри, наблюдавшего первым явление самоиндукции, принята единица генри (Гн).

Из выражения (2-3) электродвижущую силу самоиндукции, созданную в катушке, запишем следующим образом:

Из этого выражения следует вывод: величина электродвижущей силы самоиндукции прямо пропорциональна скорости изменения силы тока 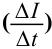 в контуре.

Из уравнения (2-4) вытекает физический смысл и единица индуктивности (или коэффициент самоиндукции): если при скорости изменения силы, тока равной 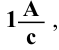в контуре возникает ЭДС самоиндукции, равная 1 вольту, то индуктивность контура будет равна 1 Гн, т.е.:

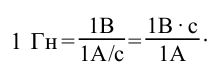
Индуктивность длинной катушки или соленоида, имеющего длину 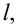с поперечным сечением S, количеством витков N, определяется с помощью следующего выражения (рис. 2.4):

Здесь: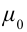 - коэффициент магнитной постоянной вакуума, количественное значение которого равно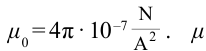-магнитная проницаемость среды внутри соленоида (с магнитной проницаемостью вещества подробнее познакомимся в следующей теме).

Явление самоиндукции можно сравнить с явлением инерции в механике. Насколько важна масса тела в явлении инерции, настолько же важна индуктивность в явлении самоиндукции. Чем больше масса, тем тело будет инертнее, и чем больше индуктивность, тем медленнее (инертнее) меняется величина тока в цепи. На вышеприведенном примере процесс медленного включения и отключения лампы, последовательно подсоединенной к катушке, можно сравнить с медленным сдвигом с места и замедленной остановкой инертного тела при движении.

Пример №9

Найдите индуктивность катушки, если при равномерном изменении сила тока от нуля до 3 А за 0,2 с в ней возникла ЭДС самоиндукции 1,5 В.
Дано: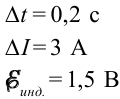  Найти: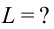

Формула: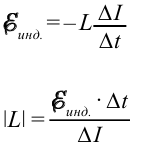

Решение: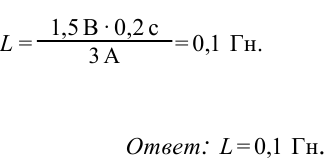
 

Магнитные свойства вещества

Во многих веществах (например, железо, никель, кобальт), в момент нахождения их в магнитном поле или когда через них пропускают ток, наблюдается намагничивание. Они, как магнит, создают вокруг себя магнитное поле. Вещества, которые намагничиваются под действием магнитного поля, называют магнетиками.

Мы узнали, что магнитное поле, создаваемое внутри катушки, прямо пропорционально силе тока. Для оценки магнитного поля внутри катушки можно провести следующий демонстрационный опыт. Общий вид демонстрационного устройства приводится на рис. 2.5 а. Оно состоит из источника тока, двух катушек, сердечников, изготовленных из различных веществ, амперметра и ключа.

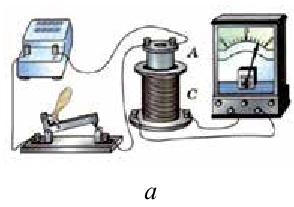
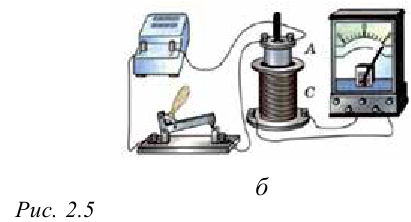
Не меняя подаваемого на катушку напряжения, будем поочередно вставлять внутрь катушки разные сердечники. В результате изменения индукции магнитного поля наблюдаем, что стрелка гальванометра отклоняется каждый раз по-разному (рис. 2.5 б).

Индукция магнитного поля, создаваемая внутри катушки, зависит от природы вводимого в нес вещества, т.е.:

Значит, индукция (В) магнитного поля, создаваемого катушкой с током в какой-либо среде, прямо пропорциональна индукции магнитного поля в вакууме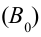 и зависит от вида среды 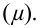Тогда из выражения (2-6) находим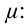

В этом уравнении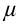 - это магнитная проницаемость среды. Она зависит от природы среды и показывает, во сколько раз отличается индукция магнитного поля в среде от индукции магнитного поля в вакууме.

Все вещества, встречающиеся в природе, по магнитной проницаемости разделяются на три вида: диамагнетики, парамагнетики и ферромагнетики.

Вещества, у которых магнитная восприимчивость меньше единицы 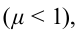называются диамагнетиками. Золото, серебро, медь, цинк и некоторые газы являются диамагнетиками. Диамагнетики, введенные в магнитное поле, его ослабляют. При приближении магнитного поля к таким веществам они удаляются от него (рис. 2.6).

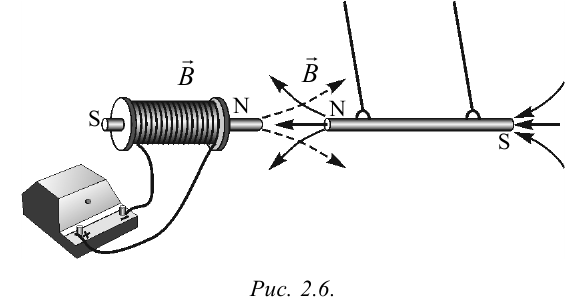
Вещества, у которых магнитная проницаемость немного больше единицы 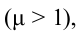называются парамагнетиками.

К парамагнетикам относятся платина, алюминий, хром, марганец, кислород. Парамагнетики, введенные в магнитное поле, немного усиливают его.

Вещества, у которых магнитная восприимчивость намного больше единицы 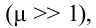называются ферромагнетиками. К ферромагнетикам относятся железо, никель, кобальт и некоторые их сплавы. Введенные в магнитное поле ферромагнетики усиливают его.

Тела, изготовленные из таких веществ, при введении их в магнитное поле притягиваются к нему (рис. 2.7).

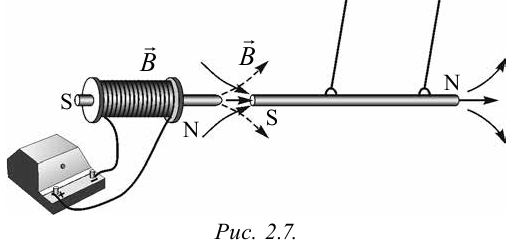
Несмотря на то, что ферромагнетиков в природе немного, они широко применяются в современной технике. Например, сердечники трансформатора, генератора тока, электродвигателя и других устройств изготавливаются из ферромагнитных материалов. В последнее время постоянные магниты нашли широкое применение в медицине. Из них изготавливают браслеты для рук, которые понижают кровяное давление.
 

Пример №10

В катушку без сердечника с индукцией магнитного поля, равной 0,50 Тл, введен ферромагнит с магнитной проницаемостью, равной 60. Во сколько раз изменится индукция магнитного поля внутри катушки?
Дано: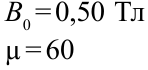  Найти: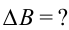

Формула: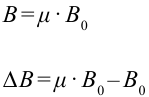

Решение: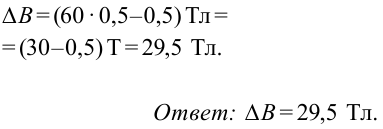

Энергия магнитного поля:

Магнитное поле, образованное вокруг проводника с током, также имеет энергию, как и электрическое поле заряженного тела. Расчет энергии магнитного поля рассмотрим на следующем примере. Пусть катушка с индуктивностью L последовательно соединена с источником тока через реостат (рис. 2.8).

Часть энергии тока, проходящего через катушку, расходуется на создание в ней магнитного поля. Согласно закону сохранения энергии, энергия, созданная током, равна работе, израсходованной для создания потока магнитной индукции, т.е.:

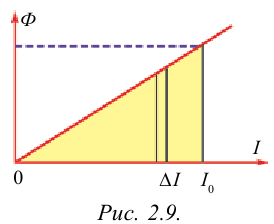
Передвигая ползунок реостата, постепенно увеличим ток, проходящий через катушку. Магнитный поток, созданный в катушке 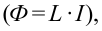прямо пропорционален проходящему по ней току, т.е. с постепенным увеличением тока линейно растет магнитный поток (рис. 2.9). Геометрический смысл площади треугольника, приведенного на рисунке, объясняет выполненную работу. Количественно эта площадь равна:

В этом случае формула вычисления энергии магнитного поля, создаваемого вокруг проводника с током, примет вид:

Значит, энергия магнитного поля контура с током равна половине произведения индуктивности на квадрат силы тока, проходящего по контуру.

Как видно из формулы (2-9), сравнивая выражение энергии магнитного поля тока с кинетической энергией движущегося тела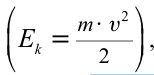

замечаем, что индуктивность похожа на физическую величину, как масса в механике. Как уже говорилось выше, масса тела играет такую же роль для изменения скорости в механике, как индуктивность в изменении силы тока в контуре.

Основу электромагнита составляет катушка соленоида. Ферромагнитный сердечник, введенный в соленоид, резко увеличивает его индуктивность. В результате усиливается магнитное поле вокруг электромагнитной катушки, и он сможет поднимать тяжелые грузы.

Электромагнитные краны, действующие на основе создаваемого магнитного поля вокруг катушки с током, нашли широкое применение в различных отраслях народного хозяйства (рис. 2.10).

Пример решения задачи

Какая должна быть сила тока в витке катушки с индуктивностью 0,2 Гн для создания энергии магнитного поля, равной 4 мДж?
Дано: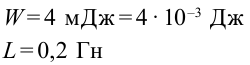  Найти: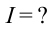

Формула: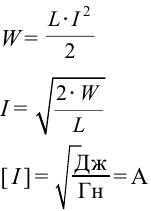

Решение: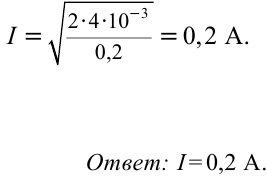

Самые важные понятия, правила и законы

• Явление электромагнитной индукции: Процесс возникновения электрического тока в замкнутом контуре, расположенном в магнитном поле, в результате изменения магнитного потока.
• Индукционный ток: Электрический ток, который возникает при изменении магнитного потока, пересекающего замкнутый контур.
• Закон электромагнитной индукции: ЭДС электромагнитной индукции, созданная в замкнутом контуре, количественно равна изменению магнитного потока, пронизывающего этот контур, и противоположна по знаку:
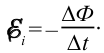
• Правило Ленца: Индукционный ток в замкнутом контуре направлен так, что создаваемый им поток магнитной индукции стремится препятствовать тому изменению потока, которое вызывает данный ток.
• Магнитный поток, созданный проводником с током: Магнитный поток (Ф), образованный проводником с током, зависит от силы тока, протекающего по нему, и индуктивности проводника:
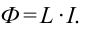
• Единица индуктивности: Если при скорости изменения силы тока, равной 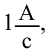в контуре образуется ЭДС самоиндукции, равная 1 вольту, то индуктивность контура будет равна 1 Гн.
• ЭДС самоиндукции  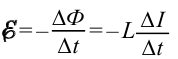: Величина электродвижущей силы самоиндукции прямо  А1  пропорциональна скорости изменения силы тока 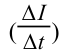в контуре.
• Магнетики :Вещества, которые намагничиваются под воздействием внешнего магнитного поля.
• Магнитная проницаемость :Зависит от природы среды и показывает отношение индукции магнитного поля среды и вакуума.
• Диамагнетики: Вещества, у которых магнитная проницаемость меньше единицы
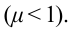
• Парамагнетики: Вещества, у которых магнитная проницаемость немного больше единицы
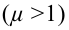
• Ферромагнетики: Вещества, у которых магнитная проницаемость намного больше единицы
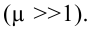
• Энергия  магнитного поля: 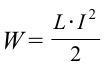  Энергия магнитного поля тока равна половине произведения индуктивности контура на квадрат силы тока, проходящего по контуру.

Явление и ЭДС электромагнитной индукции

Если проводник длиной 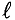пересекает магнитное поле с индукцией В со скоростью V, то в этом проводнике индуктируется ЭДС электромагнитной индукции.

Явление наведения ЭДС электромагнитной индукции в проводнике, пересекающем магнитное поле, называется электромагнитной индукцией.

Природу наведения ЭДС в пересекающем магнитное поле проводнике можно рассматривать на примере перемещения указанного выше проводника перпендикулярно линиям магнитного поля со скоростью V, вверх (рис. 9.1).

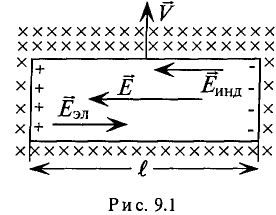
Очевидно, вместе с проводником вверх перемещаются все свободные и несвободные заряды проводника, создавая свой ток, т.е. направленное перемещение зарядов. Так как перемещающиеся направленно заряды создают ток в магнитном поле, то на каждый свободный заряд будет действовать электромагнитная сила, направление которой можно определить по правилу левой руки. Учитывая, что за направление тока принято направление перемещения положительных зарядов, ток положительных зарядов, перемещающихся вместе с проводником, направлен вверх, а ток отрицательных зарядов - вниз, т. е. противоположно току положительных зарядов.

В результате взаимодействия тока зарядов с магнитным полем на положительные заряды, в данном примере, электромагнитная сила направлена влево, а на отрицательные заряды - вправо. Таким образом, на концах рассматриваемого проводника сосредотачиваются разноименные заряды (рис. 9.1), т.е. создается ЭДС электромагнитной индукции Е.

Направление ЭДС электромагнитной индукции определяется правилом правой руки: правую руку располагают так, чтобы магнитные линии поля входили в ладонь, а отогнутый большой палец показывал направление перемещения проводника (направление скорости V), тогда вытянутые четыре пальца покажут направление индуктированной ЭДС Е (см. рис. 9.1).

Проводник с ЭДС может выполнять функцию источника электрической энергии.

Величина индуктированной ЭДС рассчитывается с учетом того, разделение зарядов в проводнике происходит под действием электромагнитных сил, напряженность которых определяется выражением

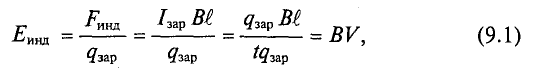
Т.е 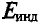- напряженность индукции - напряженность поля, со-ная электромагнитными силами и направленная так же, как ы, действующие на положительный заряд (рис. 9.1); 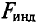-электромагнитные силы, действующие на заряды, создающие ток ядов; 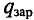- заряды, создающие ток зарядов; 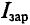— ток зарядов, направленно пересекающих магнитное поле, т.е. 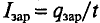(количество электричества в единицу времени); 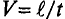— скорость перемещения проводника (зарядов), где 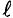— путь, пройденный за-ом за время t.

Разделенные в проводнике заряды создают в нем электрическое поле, напряженность которого 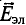направлена от положительного яда к отрицательному (рис. 9.1). Таким образом, напряженность электрического поля в проводнике 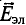направлена против напряженности индукции 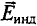. Очевидно, разделение зарядов в воднике под действием электромагнитных сил прекратится да, когда напряженность 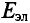станет равной :

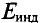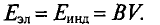
Сосредоточенные на концах проводника разделенные заряды дают в проводнике однородное электрическое поле. Следовательно, напряжение на концах проводника согласно (1.13) будет равно

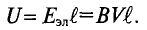
Так как проводник разомкнут (холостой ход), то напряжение U концах проводника равно его ЭДС — Е (см. раздел 2.6).

Тогда 

Так определяется ЭДС электромагнитной индукции Ев проводке длиной пересекающем однородное магнитное поле с индукцией В перпендикулярно его направлению со скоростью V.

Если же проводник пересекает поле под углом а (рис. 9.2), то ЭДС - Е в этом проводнике определяется выражением

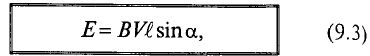
где а — угол между направлением движения проводника и магнитным полем.

Если проводник с индуктированой ЭДС замкнуть, то в замкнутой цепи проводника появится ток, который, как и ЭДС, называется индуктированным.

Направление индуктированного тока совпадает с направлением индуктированной ЭДС.

Преобразование энергий. Правило Ленца

Преобразование механической энергии в электрическую

Если проводник пересекает магнитное поле, то в нем индуктируется ЭДС электромагнитной индукции. При замыкании проводника в цепи появится индуктированный ток. Таким образом, механическая энергия, затраченная на перемещение проводника в магнитном поле, преобразуется в электрическую энергию тока в этом проводнике.

Подобное преобразование механической энергии в электрическую имеет место в электрических генераторах.

Направление индуктированного тока в проводнике определяется по правилу правой руки (рис. 9.3). Индуктированный ток взаимодействует с магнитным полем, в результате чего на проводник с током 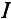 действует электромагнитная сила Р, направление которой определяется по правилу левой руки. Как видно (рис. 9.3), эта сила направлена против скорости перемещения проводника V, которая является причиной возникновения индуктированного тока.

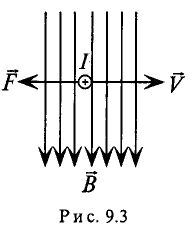
Это и легло в основу правила Ленца, согласно которому индуктированный ток всегда противодействует причине, вызвавшей его (т. е. сила F, вызванная индуктированным током I, противодействует перемещению проводника со скоростью V, которое и является причиной, вызвавшей этот ток).

Затраченная на перемещение проводника механическая мощность компенсируется мощностью электромагнитных сил FV, т. е.

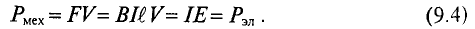
Уравнение (9.4) устанавливает количественную сторону преобразования механической энергии в электрическую. Таков баланс плотностей при преобразовании механической энергии в электрическую.

Преобразование электрической энергии в механическую

и по проводнику сопротивлением R, расположенном в магом поле с индукцией В, проходит ток I, созданный источник с ЭДС Е и внутренним сопротивлением 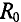, то на этот проводник будет действовать электромагнитная сила F, за счет которой проводник будет перемещаться (рис. 9.4).

Таким образом, электрическая энергия тока 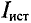преобразуется в механическую энергию движения этого проводника под действием электромагнитной силы F.

Такое преобразование электрической энергии в механическую имеет место в электрических двигателях.

Направление электромагнитной силы определяется по правилу левой руки. При движении проводника в том же магнитном поле действием электромагнитной силы F в проводнике, пересекаем это поле, индуктируется ЭДС электромагнитной индукции.

Направление индуктированного тока 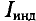, вызванного этой 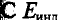в замкнутой цепи, определяется по правилу правой руки 9.4).

Как видно, индуктированный ток 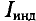направлен против тока источника 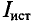в сопротивлении R. Тем самым еще раз подтверждается правило Ленца: индуктированный ток всегда противодействует причине, вызвавшей его, 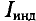направлен против тока взаимодействие которого с магнитным полем создает электромагнитную силу F, являйся причиной создания .

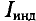Для замкнутой цепи, изображенной на рис. 9.4, величина образованной электрической энергии в механическую определяется на основании второго закона Кирхгофа:

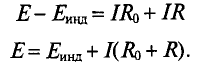
множив левую и правую части равенства на 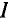, получаем

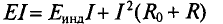
или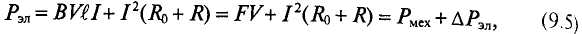

где 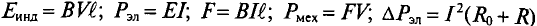- мощность электрических потерь в рассматриваемой цепи;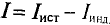

Таков баланс мощностей преобразования электрической энергии в механическую.

ЭДС электромагнитной индукции в контуре и катушке

Допустим, что проводник длиной 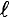 пересекает однородное магнитное поле с неравномерной скоростью 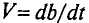(рис. 9.5). Следовательно, в этом проводнике индуктируется переменная ЭДС электромагнитной индукции

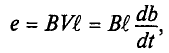
где е — мгновенное значение переменной ЭДС; db — бесконечно малый отрезок пути, пройденный проводником за время dt.

За время dt проводник пересекает элементарную площадку магнитного поля 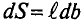. Следовательно,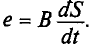

Пронизывающий проводник элементарный магнитный поток dФ магнитного поля равен

dO = BdS.

Тогда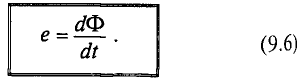 

Таким образом, ЭДС электромагнитной индукции в проводнике равна скорости изменения магнитного потока в этом проводнике.

Из уравнения (9.6) следует, что для создания ЭДС электромагнитной индукции в проводнике проводник должен пересекаться переменным магнитным потоком, поскольку при постоянном значении магнитного потока его производная равна нулю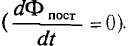

Для того чтобы магнитный поток, пронизывающий проводник, был переменным, необходимо, чтобы или проводник пересекал неподвижное магнитное поле, или магнитное поле пересекаю неподвижный проводник, или проводник должен пересекаться переменным по величине или направлению магнитным потоком выражение (9.6) получено для случая пересечения прямолинейным проводником однородного магнитного поля с неравномерной скоростью под углом 90°.

Это же выражение (9.6) справедливо для определения ЭДС электромагнитной индукции в проводнике любой формы, перемещающем любое магнитное поле под любым углом, практике возникает необходимость определить ЭДС электромагнитной индукции в замкнутом контуре или катушке.

Если контур пересекает неоднородное магнитное поле со скоростью V, то в левом проводнике этого контура, пересекающем за dt элементарный магнитный поток 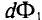индуктируется 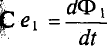, а в правом проводнике контура, пересекающем за время dt элементарный магнитный поток 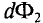, индуктируется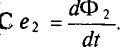 
Направление ЭДС в проводниках контура определяется по правилом правой руки.

Эти ЭДС, как видно на рис. 9.6, направлены в контуре навстречу друг Следовательно, суммарная ЭДС электромагнитной индукции в контуре на их разности

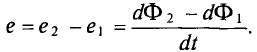
Положительное направление ЭДС но с направлением вращательного движения рукоятки буравчика, поступательное движение которого совпадает с направлением магнитного поля.

Приращение магнитного потока 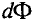 в контуре за время dt, полученное при перемещении контура влево (рис. 9.6), равно 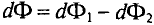, так как  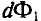вошел в контур, a 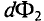вышел из контура за это время, следовательно, ЭДС электромагнитной индукции в контуре

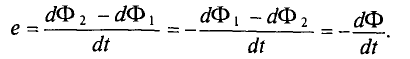
ЭДС электромагнитной индукции в контуре определяется скоростью изменения магнитного потока в этом контуре, взятой с обратным знаком: 

Знак «минус» здесь отражает правило Ленца, которое для контура гласит так: индуктированный в контуре ток, наведенный индуктированной ЭДС, противодействует изменению магнитного потока в этом контуре.

Индуктированный ток в контуре изменяет свое направление в зависимости от того, уменьшается или увеличивается магнитный поток в этом контуре (рис. 9.7) при неизменном направлении его.

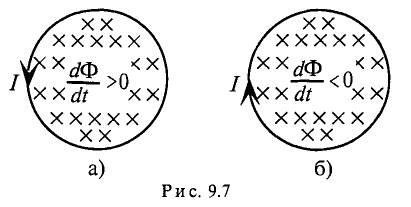
То есть при увеличении магнитного потока (рис. 9.7а) индуктированный ток противодействует этому увеличению, а при уменьшении потока индуктированный ток противодействует его уменьшению (рис. 9.76).

Если магнитное поле изменяется в катушке, состоящей из W витков (рис. 9.8а), то в каждом витке (контуре) этой катушки индуктируется 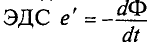. Во всех витках этой катушки ЭДС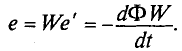 

Произведение 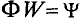называется потокосцеплением. Тогда ЭДС, индуктированная переменным магнитным потоком в катушке, будет определяться:

Таким образом, ЭДС электромагнитной индукции в катушке равна скорости изменения потокосцепления в ней, взятой с обратным знаком. Знак «минус» является отражением правила Ленца.

Явление и ЭДС самоиндукции

Если по катушке с числом витков W(puc. 9.8а) проходит ток /, то этот ток создает в катушке магнитный поток Ф, величина которого пропорциональна току. Очевидно, пропорционально этому току и потокосцепление .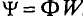

Следовательно, отношение у для данной катушки — величина постоянная. Эта постоянная величина обозначается буквой L и называется индуктивностью катушки:

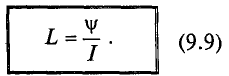
Таким образом, индуктивность L является параметром определенной катушки, а также параметром любого проводника и контура.

Единицей индуктивности является генри:

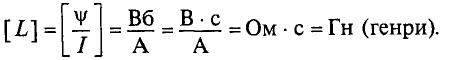
Магнитный поток, созданный в катушке (рис. 9.8а) с числом мотков W током I, будет равен согласно (8.1)

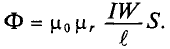
Тогда потокосцепление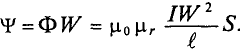

Индуктивность катушки определяется выражением

Таким образом, индуктивность катушки пропорциональна квадрату числа витков катушки и зависит от габаритов и материала магнитопровода этой катушки.

Изменять индуктивность катушки можно изменением магнитной проницаемости магнитопровода 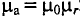при разомкнутом магнитопроводе катушки сердечник можно вставлять или вынимать из катушки, а при замкнутом сердечнике из ферромагнитного материала можно изменять ток катушки (рис. 8.4).

Если по катушке с индуктивностью L (рис. 9.86) пропустить переменный ток i, то он создает в катушке переменный магнитный ок, который индуктирует в витках катушки ЭДС самоиндукции .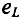

Явление наведения ЭДС самоиндукции в проводнике, контуре или тушке, вызванное изменением тока в самом проводнике, контуре и катушке, называется явлением самоиндукции.

ЭДС самоиндукции в катушке можно определить, используя выражения (9.8) и (9.9):

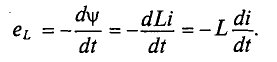
Таким образом, ЭДС самоиндукции 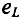в проводнике, контуре или катушке пропорциональна скорости изменения тока в этом проводнике, контуре или катушке, взятой со знаком «минус», т. е.

Знак «минус» отражает здесь правило Ленца, которое в данном случае можно сформулировать так: индуктированный в катушке ток, вызванный ЭДС самоиндукции, противодействует изменению тока, вызвавшего эту ЭДС.

Так, например, если ток i катушки увеличивается., то ЭДС самоиндукции (индуктированный ток) противодействует этому увеличению; если же ток i катушки уменьшается, то индуктированный ток противодействует его уменьшению.

Из формулы (9.11) видно, что индуктивность L как параметр проводника, контура и катушки характеризует их с точки зрения наведения в них ЭДС самоиндукции, т. е. чем больше индуктивность L, тем больше ЭДС самоиндукции в них при неизменной скорости изменения тока.

Если по катушке с индуктивностью L проходит ток I, то в магнитном поле этой катушки накапливается энергия, величина которой определяется:

Явление и ЭДС взаимоиндукции

Если две или несколько катушек расположить так, что магнитный поток одной из них пронизывает витки остальных, то такие катушки называют магнитосвязанными.

Если по одной из магнитосвязанных катушек, например первой 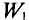(рис. 9.9а), пропустить ток 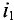то он создает в этой катушке магнитный поток 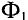, пропорциональный 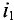часть которого  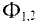пронизывает витки второй катушки 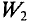, создавая потокосцепление 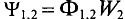, пропорциональное 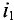. Часть магнитного потока 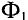рассеивается .

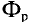Если по второй катушке 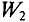(рис. 9.9а) проходит ток 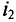, то он создает в ней магнитный поток 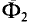, пропорциональный 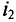, часть которого 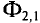пронизывает витки первой катушки 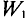, создавая потокосцепление  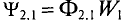пропорциональное .

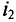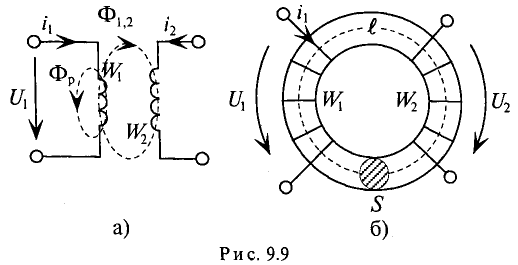
Cледовательно, для двух магнитосвязанных катушек отношение

Величина постоянная, обозначается буквой М и называется мной индуктивностью этих катушек.

Взаимная индуктивность М — это параметр магнитосвязанных проводников, контуров или катушек.

Взаимная индуктивность М измеряется в генри

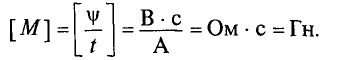
Если на магнитопроводе неразветвленной магнитной цепи с. 9.96) расположены две катушки 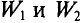, то при отсутствии рассеивания (магнитный поток каждой катушки полностью закается в магнитопроводе и пронизывает другую катушку) взаимная индуктивность этих катушек определяется выражением

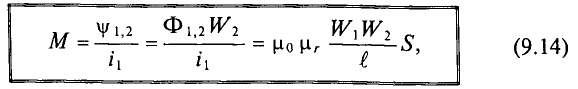
где 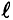 — общая длина магнитопровода; S — сечение магнитопровода, 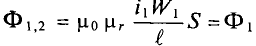(согласно выражению (8.1)).

Таким образом, взаимная индуктивность двух магнитосвязанных пушек пропорциональна произведению числа витков этих катушек и зависит от габаритов и материала магнитопровода, на ковром расположены эти катушки.

Каждая из рассмотренных магнитосвязанных катушек (рис. 9.96) обладает индуктивностью (см. (9.10))

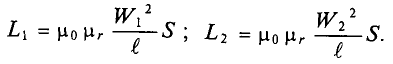
Произведение этих индуктивностей будет равно

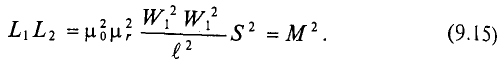
Следовательно, при отсутствии рассеяния величина взаимной индуктивности

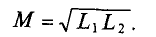
В общем случае

Коэффициент К называют коэффициентом связи двух магнитосвязанных катушек

Коэффициент связи К показывает, какая часть созданного катушками магнитного потока пронизывает одновременно обе магнитосвязанные катушки.

Коэффициент связи может изменяться от нуля до единицы, т. е. 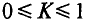. При отсутствии рассеяния магнитного потока К= 1, а при отсутствии магнитной связи К= 0.

Если по одной из магнитосвязанных катушек (рис. 9.96), например первой, пропустить переменный ток 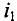, то он создает в ней переменный магнитный поток 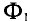, часть которого 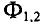пронизывает витки второй катушки 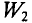и индуктирует в них ЭДС взаимоиндукции .

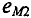Явление наведения ЭДС взаимоиндукции в одной из магнитосвязанных катушек, вызванное изменением тока в другой катушке, называется явлением взаимоиндукции.

ЭДС взаимоиндукции во второй катушке будет равна

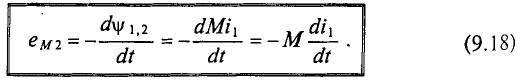
То есть ЭДС взаимоиндукции в одной из магнитосвязанных катушек пропорциональна скорости изменения тока в другой катушке со знаком «минус».

Следовательно 

Знак «минус» отражает правило Ленца.

Взаимная индуктивность М как параметр взаимосвязанных проводников, контуров и катушек характеризует явление взаимоиндукции с точки зрения наведения ЭДС взаимоиндукции в одном элементе (катушке 2), вызванное изменением тока в другом элементе (катушке 1), магнитосвязанном с ним.

Явление взаимоиндукции лежит в основе работы электрических трансформаторов.

Сложенное к первичной обмотке трансформатора напряжение 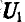 уравновешивается падением напряжения на обмотке  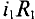самоиндукции этой обмотки  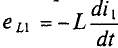и ЭДС взаимоиндукции в той же обмотке 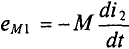(см. рис. 9.96).

Применяя второй закон Кирхгофа (для мгновенных значений), можно записать для первичной обмотки

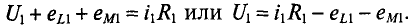
Тогда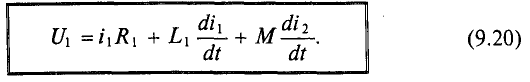 
Пo аналогии можно записать выражение для определения напряжения U₂ на вторичной обмотке, к которой подключается потребитель:

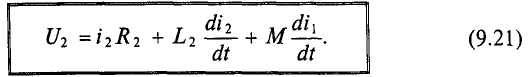
Перед ЭДС взаимоиндукции в (9.20) и (9.21) может стоять знак минус, если имеет место встречное включение, т. е. 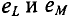в обмотке направлены в разные стороны.

Как видно, в обмотках трансформатора имеет место явление электромагнитной индукции, самоиндукции и взаимоиндукции. Чем же отличаются эти явления?

Природа всех этих явлений одинакова — переменный магнитный поток индуктирует в проводнике, контуре или катушке перечную ЭДС. Если происхождение этого потока произвольно, то индуктирует ЭДС электромагнитной индукции е. Если этот магнитный поток создан током, проходящим по самому проводнику, контуру или катушке, то он индуктирует ЭДС самоиндукции 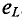. Если магнитный поток создан током, проходящим по одному элементу цепи (например, первому контуру) магнитосвя-занному с другим элементом цепи (например, вторым контуром), то он наводит во втором контуре ЭДС взаимоиндукции ем.

Вихревые токи

Сердечники якоря и полюсов электрических машин, трансформаторов, дросселей и других аппаратов, по обмоткам которых проходит переменный ток, выполняются обычно из электротехнической стали, представляющей собой ферромагнитный материал и одновременно проводник.

Переменный ток в обмотках массивных сердечников (рис. 9.10а) создает в этих сердечниках переменный магнитный поток Ф, направленный вдоль сердечника перпендикулярно площади его поперечного сечения. Переменный магнитный поток в каждом сечении сердечника индуктирует ЭДС электромагнитной индукции. Эта ЭДС в каждом слое массивного сердечника создает токи, которые замыкаются в этом слое проводящего материала (рис. 9.10а).

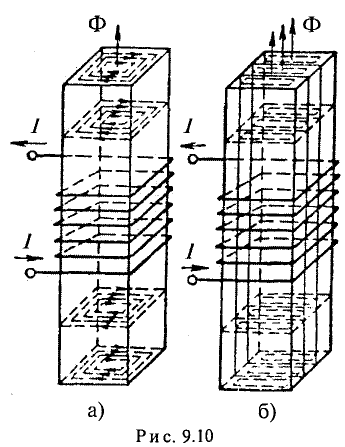
Эти токи называются вихревыми токами.

Между вихревыми токами в каждом слое массивного сердечника и током /, создающим эти токи, существует не электрическая, а электромагнитная связь.

Вихревые токи вызывают нагрев стальных сердечников электромагнитных аппаратов и снижают их КПД за счет потерь энергии, которая тратится на нагрев.

Потери, вызванные вихревыми токами в токопроводящих сердечниках, называются потерями на вихревые токи. Для уменьшения потерь на вихревые токи стальные сердечники, по обмоткам которых проходит переменный ток, выполняют из листовой стали (рис. 9.106). Для этой цели используются тонкие листы толщиной 0,35 или 0,5 мм, малое сечение которых создает большое сопротивление вихревым токам (см. (2.5)) и уменьшает их. Для уменьшения вихревых токов листы стали изолируются друг от друга специальным лаком. Кроме того, для ослабления вихревых а следовательно, и потерь на них в электротехническую вводится кремний, благодаря чему увеличивается удельное сопротивление, а следовательно, и сопротивление сердечника в (см. (2.8)).

Направление вихревых токов в сердечниках определяют по правилом Ленца.

Вихревые токи применяются для индукционной плавки метал закалки стальных деталей (шестерен и коленчатых валов), аукционных печах вихревые токи используют для нагрева-заготовок. Принцип действия индукционных приборов электрических счетчиков) базируется на вихревых токах. Вихревые токи используются в электроизмерительных устройствах, магнитоиндукционных успокоителях колебаний некоторых приборов.