Электрические цепи с взаимной индуктивностью

Содержание:

Электрические цепи с взаимной индуктивностью:

Элементы электрической цепи могут быть между собой связаны общим магнитным полем и тогда изменение тока в одном из элементов является причиной наведения э. д. с. в другом элементе. Такое взаимное влияние элементов цепи называется их индуктивной связью.
Если индуктивными связями пренебречь нельзя, то расчет электрической цепи несколько усложняется.

Взаимоиндуктивное сопротивление

Сопротивление в электрической цепи, обусловленное взаимоиндукцией, аналогично сопротивлению, обусловленному самоиндукцией, так как э. д. с. взаимоиндукции влияет на режим цепи с качественной стороны так же, как и э. д. с. самоиндукции.

Одноименные и разноименные зажимы индуктивно-связанных катушек
Ранее было дано определение согласного и встречного включения катушек.
При согласном включении магнитные потоки самоиндукции и взаимоиндукции в обеих катушках по направлению совпадают, поэтому э. д. с. самоиндукции и взаимоиндукции в каждой катушке также направлены одинаково.

При встречном включении магнитные потоки, а также э. д. с. самоиндукции и взаимоиндукции по направлению противоположны.

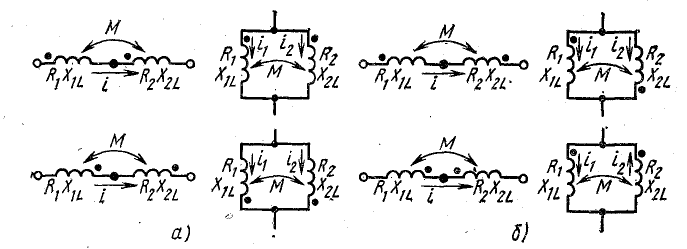
На схемах замещения взаимная индуктивность обозначается буквой М и дугой, объединяющей два индуктивно-связанных элемента (рис. 16.1). Для того чтобы различать согласное и встречное включения, на схемах обозначают также начала индуктивно-связанных катушек, отмечая их точками или звездочками.
 

Зажимы индуктивно-связанных катушек называют одноименными (начала или концы), если при согласном включении положительное направление токов, принятое на схеме, относительно этих зажимов одинаково (рис. 16.1, а). При встречном включении (рис. 16.1, б) ток в одной катушке направлен к началу, а в другой — к концу.
 

Разметка зажимов на основе опыта

Направление магнитных потоков катушек зависит от их взаимного расположения и направления намотки витков. При отсутствии сведений о расположении начал и концов можно провести простой опыт, для которого кроме самих индуктивно-связанных катушек требуется гальванический элемент (или аккумулятор) и гальванометр (рис. 16.2).

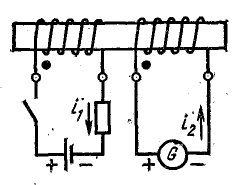
Рис. 16.2. Схема опыта для разметки зажимов катушек

Одну из катушек через ключ присоединяют к гальваническому элементу, к зажимам другой подключают гальванометр. В момент замыкания ключа К возникают токи в обеих катушках, причем ток i₂ создает магнитный поток, направленный навстречу потоку первой катушки (правило Ленца). Поэтому при включении гальванического элемента токи i₁ и i₂ направлены противоположно относительно одноименных зажимов. Направление тока i₁ известно, так как известна полярность источника питания, а направление тока i₂ определяется по отклонению гальванометра.

Ток i₂ направлен к положительному зажиму гальванометра, если стрелка его отклоняется по шкале (шкала односторонняя).

Одноименными зажимами катушек являются зажимы, к которым присоединены положительные зажимы источника и гальванометра; другие два зажима также одноименны.

Определение взаимоиндуктивного сопротивления

Рассматривая две индуктивно-связанные катушки, запишем выражения э. д. с. самоиндукции и взаимоиндукции, возникающие при синусоидальных токах в обеих катушках, направленных одинаково относительно одноименных зажимов. Э. д. с. и напряжения:
от самоиндукции                                              от взаимоиндукции
в первой катушке

    

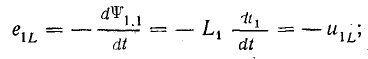
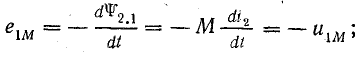
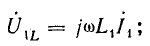
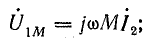
во второй катушке

    

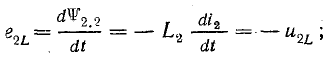
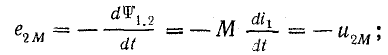
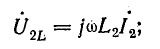
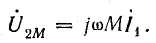
Э. д. с. и напряжения самоиндукции и взаимоиндукции имеют одинаковые знаки так как при согласном включении потоки самоиндукции и взаимоиндукции направлены одинаково. Создаваемый ими эффект противодействия току учитывается введением в расчет индуктивного сопротивления ωL₁, ωL₂ и взаимоиндуктивного сопротивления ωМ.
При встречном включении катушек э. д. с. и напряжения самоиндукции и взаимоиндукции будут иметь разные знаки:

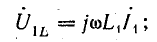
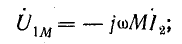
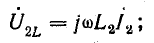
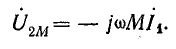
Комплексные индуктивное и взаимоиндуктивное сопротивления записывают аналогично:

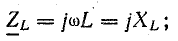
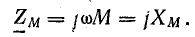
Задача 16.1.

Для определения параметров двух магнитно-связанных катушек провели измерения.
1. По схеме рис. 16.3, а измерили ток и напряжение на каждой катушке, включив их последовательно в сеть постоянного тока:

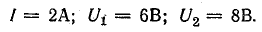
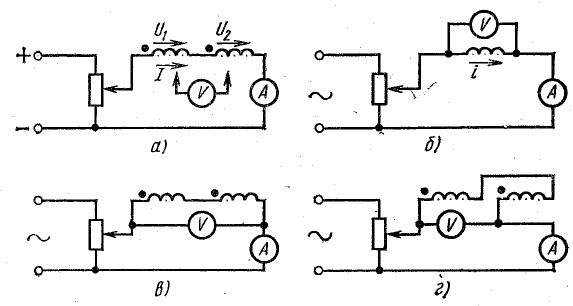
Рис. 16.3. К задаче 16.1

2.    По схеме рис. 16.3, б измерили в каждой катушке ток и напряжение, включив их порознь в сеть переменного тока:

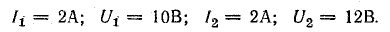
3.    По схеме рис. 16.3, в измерили ток и напряжение, включив катушки согласно и последовательно в сеть переменного тока:

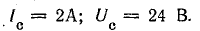
4.    По схеме рис. 16.3, г измерили ток и напряжение, включив катушки встречно и последовательно в сеть переменного тока:

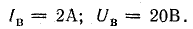
Определить активные сопротивления, индуктивности и взаимоиндуктивность катушек, если частота в сети переменного тока 50 Гц.
Решение. Первый опыт позволяет определить активные сопротивления катушек, пренебрегая увеличением сопротивления от поверхностного эффекта:
 
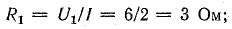
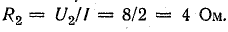
Второй опыт позволяет определить полные сопротивления катушек переменному току при отсутствии взаимного влияния, а затем рассчитать индуктивности:
 
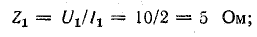
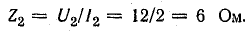
Индуктивные сопротивления:


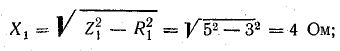
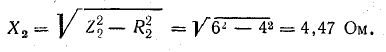
Индуктивности:


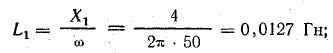
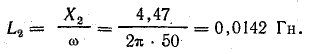
По результатам третьего и четвертого опытов определим взаимную индуктивность.
При согласном включении

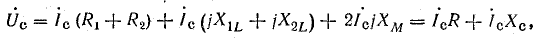
где

  
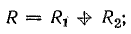
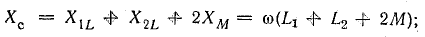
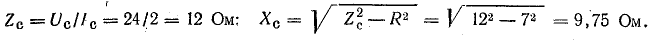9,75 Ом.

При встречном включении

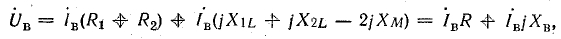
где

  

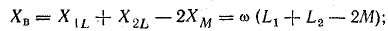
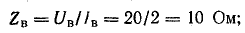
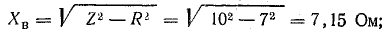
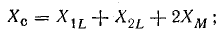
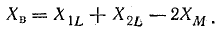
Вычтем второе уравнение из первого:

 .

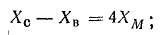
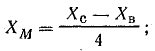
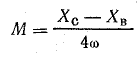Расчет электрических цепей с взаимной индуктивностью

Особенность расчета электрических цепей с взаимной индуктивностью состоит в том, что к параметрам R, L, С добавляется четвертый параметр М. Кроме того, необходимо учитывать, что э. д. с. взаимоиндукции и самоиндукции в одном и том же элементе цепи могут по направлению совпадать или быть противоположными.

Последовательное соединение

Для расчета неразветвленной цепи с взаимной индуктивностью (рис. 16.4) можно составить уравнение по второму закону Кирхгофа:

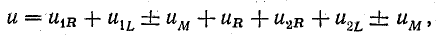
или


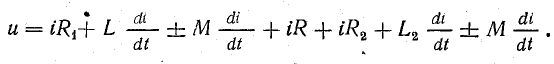
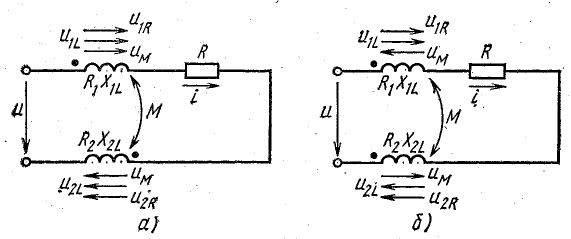
Рис. 16.4. К расчету неразветвленной цепи со взаимной индуктивностью

Те же уравнения в символической форме через действующие значения тока и напряжения должны быть записаны так:

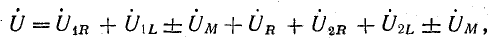
или


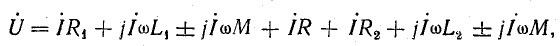
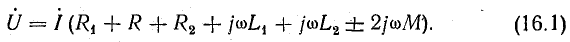
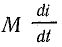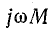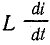При согласном включении (рис. 16.4, а) напряжение взаимоиндукции u_M по направлению совпадает с напряжением самоиндукции u_L, поэтому слагаемые , или , и , или 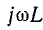, имеют в уравнениях одинаковые, в данном случае положительные, знаки. При встречном включении (рис. 16.4, б) эти слагаемые имеют разные знаки.
Из уравнения (16.1) при заданном напряжении определяется ток, а при заданном токе — напряжение.

Параллельное соединение

Для примера рассмотрим параллельное соединение двух катушек, имеющих сопротивления R₁, R₂, индуктивности L₁, L₂ и взаимоиндуктивность М (рис. 16.5).
Из схемы видно, что относительно одноименных зажимов токи в обеих катушках направлены одинаково, поэтому падения напряжения, обусловленные взаимоиндуктивностью, в соответствующие уравнения войдут с положительным знаком:

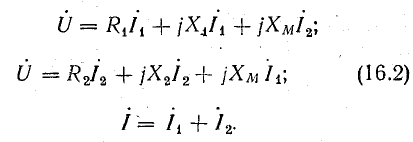
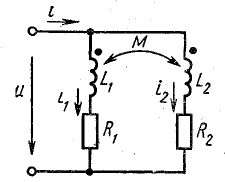
Рис. 16.5. К расчету разветвленной цепи со взаимной индуктивностью

Решение этой системы уравнений дает

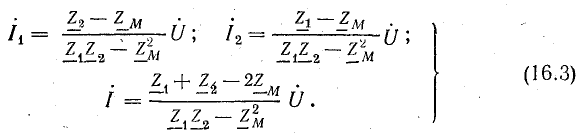
Из последнего равенства находят входное комплексное сопротивление данной цепи

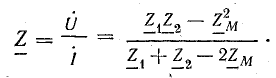
Аналогично определяют токи в случае встречного включения катушек, с той лишь разницей, что в уравнения (16.2) слагаемые, обусловленные взаимоиндуктивностыо, войдут со знаком минус.

Разветвленная цепь

В качестве примера рассмотрим схему рис. 16.6, для которой запишем уравнения с учетом взаимных индуктивностей.
1. Для контура 1-2-3-4-1


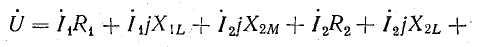
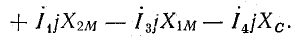
2. Для контура 2-2'-3'-3-2

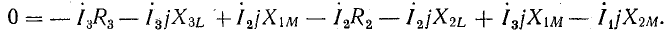
3. Для узла 2

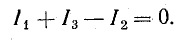
Знаки перед слагаемыми определяют согласно выбранным положительным направлениям тока и направлению обхода контуров; учитывают также включение катушек: согласное или встречное.
С этой точки зрения рассмотрим уравнение п. 2.

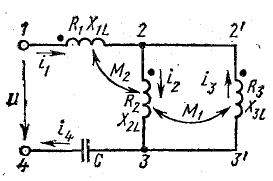
Рис. 16.6. К расчету разветвленной цепи с индуктивной связью элементов

Направление обхода контура по часовой стрелке в обоих участках контура — против тока. Поэтому падения напряжения в активных и индуктивных сопротивлениях записаны в правой части уравнения со знаком минус. При определении знака падения напряжения, обусловленного э. д. с. взаимоиндукции, дополнительно учитывается согласное или встречное включение катушек: на участке 3-2 знаки э.д. с. самоиндукции между второй и первой катушками совпадают, так как эта катушки включены согласно; поэтому 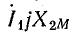, так же как и 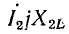, имеет отрицательный знак. Падение напряжения во второй катушке, обусловленное взаимоиндукцией с третьей катушкой, включенной с ней встречно, взято со знаком плюс, так как направления э. д.с. самоиндукции второй катушки и взаимоиндукции с третьей катушкой не совпадают.
В данном случае для определения токов в схеме нужно решить систему четырех уравнений, включая уравнение 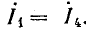Одно из контурных уравнений целесообразно использовать для проверки решения.

Задача 16.3.

Определить ток и напряжение на участках цепи (рис. 16.7, а), построить векторную диаграмму при согласном включении катушек вариометра, как показно на рис. 16.7, б. Параметры катушек: R₁ = 5 Ом, L₁ = 0,03 Гн, R₂ = 5 Ом, L₂ = 0,1 Гн. Взаимоиндуктивность М = 0,05 Гн. Сопротивление нагрузки 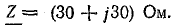Напряжение сети U = 220 В. Угловая частота ω = 1000 рад/с.

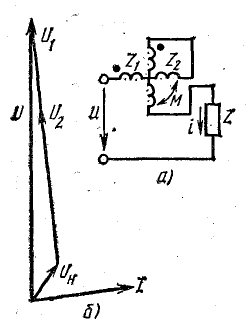
Рис. 16.7. К задаче 16.3

Решение. При согласном включении катушек вариометра


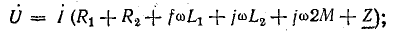
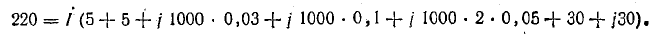
Ток в цепи

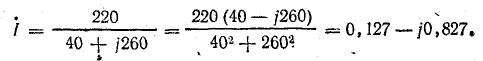
Напряжения на участках:
на первой катушке вариометра

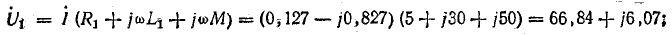
на второй катушке вариометра

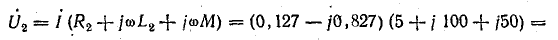
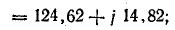
на нагрузке

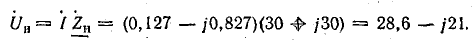
Для построения векторной диаграммы (рис. 16.7, б) можно взять масштабы: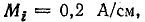

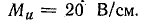
Трансформатор без ферромагнитного сердечника

Трансформаторы без ферромагнитного сердечника (воздушные) широко применяются в устройствах, работающих на высоких частотах, например в радиотехнике. Воздушный трансформатор состоит из двух индуктивно-связанных катушек (обмоток) (рис. 16.8).

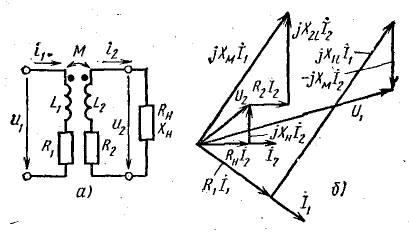
Рис. 16.8. Схема и векторная диаграмма воздушного трансформатора

Векторная диаграмма воздушного трансформатора

Электрическая схема воздушного трансформатора не имеет особенностей: к первичной обмотке подведено напряжение U₁ от некоторого источника энергии, а ко вторичной обмотке подключена нагрузка. Индуктивная связь обмоток характеризуется взаимоиндуктивностью М. Принятые на схеме рис. 16.8, а положительные направления токов и разметка одноименных зажимов показывают, что катушки включены встречно. (15.4)
По. второму закону Кирхгофа для контуров первичной и вторичной обмоток можно записать уравнения напряжений

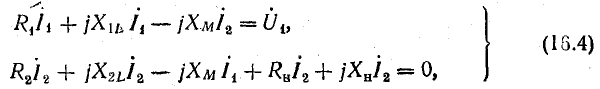
где R₁, X_1L; R₂Х_2L и R_н, Х_н — сопротивления обмоток и нагрузки; Х_М — взаимоиндуктивное сопротивление обмоток.
Векторная диаграмма рис. 16.8, б построена согласно уравнениям (16.4), причем известным принят ток I₂ и вектор этого тока отложен в произвольном направлении. Далее нанесены векторы падений напряжения в сопротивлениях вторичной обмотк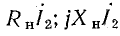и  и 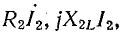 сумма которых равна вектору .
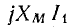Величину тока I₁ определяют на основе векторной диаграммы:
длина вектора 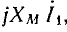выраженная в вольтах, делится на сопротивление Х_М. Вектор тока 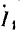отложен перпендикулярно вектору 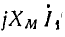с учетом отставания вектора тока.
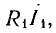
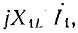
Далее отложены векторы падений напряжения в первичной обмотке  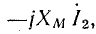сумма которых равна вектору первичного напряжения .

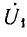Вносимые сопротивления

Из уравнений (16.4) можно выразить ток:

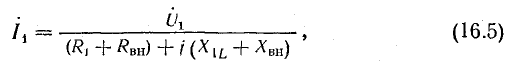
где


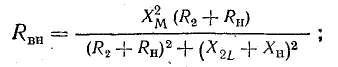
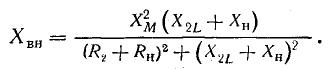
Величины R_вн и Х_вн называются вносимыми сопротивлениями (вносятся из второго контура в первый).

Из уравнения (16.5) видно, что воздушный трансформатор со стороны первичной обмотки может рассматриваться как двухполюсник с сопротивлениям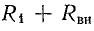и и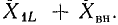
Условию передачи максимальной мощности из первого контура во второй соответствуют равенства 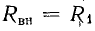и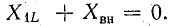

Эквивалентная схема замещения воздушного трансформатора

Уравнения (16.4) перепишем в следующем виде:


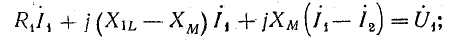
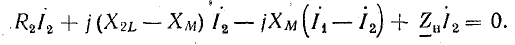
Этим уравнениям удовлетворяет схема без индуктивной связи (рис. 16.9).

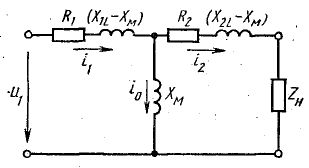
Рис. 16.9. Схема замещения воздушного трансформатора

Замена схемы трансформатора эквивалентной схемой без индуктивной связи позволяет анализировать его как обычную электрическую цепь, применяя общие методы расчета.

Рассмотрим случай, когда обмотки имеют одинаковое число витков: 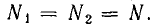 Разность такова:


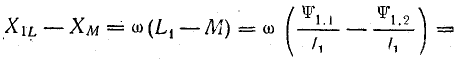
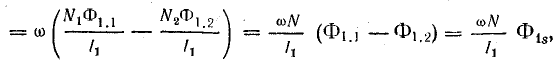
где Ф_1s — магнитный поток рассеяния первичной обмотки; 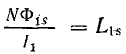 — индуктивность рассеяния первичной обмотки.
Следовательно, 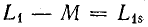; аналогично, 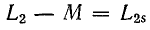— индуктивность рассеяния вторичной обмотки.
Намагничивающая сила обмоток является результатом действия той и другой обмоток, но вторичная обмотка, согласно правилу Ленца, действует против первичной, т. е.

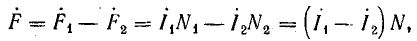
но 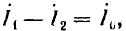поэтому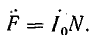
Можно считать, что ветвь с током I₀ создает намагничивающую силу трансформатора, поэтому она и называется намагничивающей ветвью.
Таким образом, в эквивалентной схеме замещения трансформатора индуктивные сопротивления обмоток обусловлены потокосцеплением рассеяния, а рабочим потоком является магнитный поток взаимоиндукции.