Электрические цепи постоянного тока

Содержание:

Расчет электрических цепей постоянного тока:

Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.

Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.

Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.

Законы Кирхгофа

Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I₁ + I₂ — I₄ — I₇ = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I₁ + I₂ = I₄ + I₇.                      (4.2)

Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.

Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V₁. Потенциал каждой последующей точки выразим относительно точки предыдущей: V₂ = V₁ + Е₁; V₃ = V₂ — I₁R₁; V₄ = V₃ — I₄R₄; V₅ = V₄ — E₃; V₆ = V₅ + I₆R₆; V₁ = V₆ — I₃R₃.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре

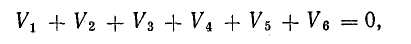
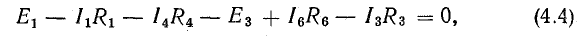
или

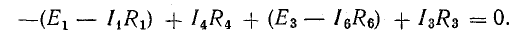
В этом уравнении напряжения ветвей

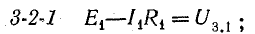
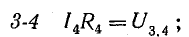
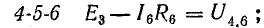
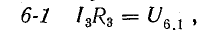
поэтому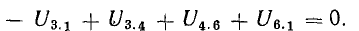

В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:

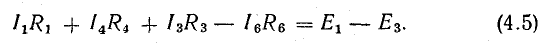
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:

Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.

Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.

При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1

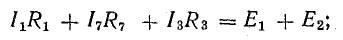
для 3-4-6-3

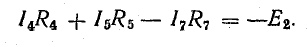
Неразветвленная электрическая цепь

Элементы неразветвленной электрической цепи соединены между собой последовательно.
 

Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.

Общий случай последовательного соединения

Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):

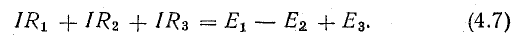
Ток в цепи

При обходе контура видно, что относительно направления обхода э. д. с. Е₁ и Е₃ направлены одинаково, т. е. согласно, а э. д. с. Е₂ — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E₁ и Е₃ вырабатывают электрическую энергию, а элемент с э. д. с. Е₂ ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е₁ и Е₃ разряжаются, а источник Е₂ заряжается.
В элементах цепи, характеризующихся сопротивлениями R₁, R₂ и R₃, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.

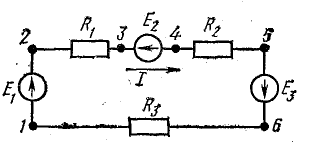
Рис. 4.1. Схема неразветвленной электрической цепи

Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е₂ в левую часть: 

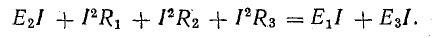
Получим уравнение баланса мощности - для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.

Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.

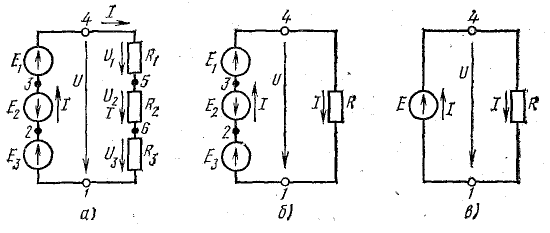
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи

Последовательное соединение пассивных элементов

Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].

Вынеся I за скобку, получим

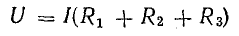
или

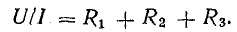
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:

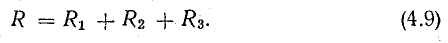
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:

т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.

Последовательное соединение источников э.д.с.

Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1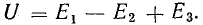
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)

и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.

Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле

где Е_n — э. д. с. одного элемента; n — число элементов в батарее.

Согласно составленной эквивалентной схеме (рис. 4.2, в),

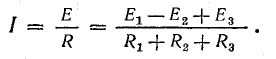
Потенциальная диаграмма

В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е₁, а при переходе от точки 2 к точке 3 — снижается на величину U_2.3 = IR₁. При переходе от точки 3 к точке 4 потенциал понижается на величину U_3.4 = —E₂. 

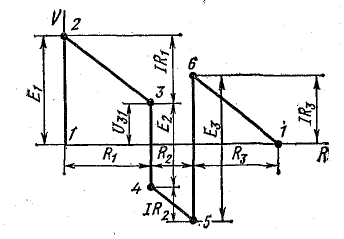
Рис. 4.3. Потенциальная диаграмма электрической цепи

Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.

Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.

Потенциалы точек цепи найдены согласно равенствам

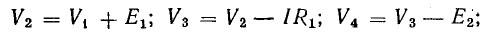
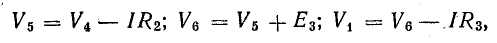
причем потенциал точки 1 принят равным нулю.

Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
 

Задача 4.3.

Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора E_г = 120 В; внутреннее сопротивление r_г = 1,0 Ом, э. д. с. батареи Е_а = 72 В, внутреннее сопротивление r_а = 3 Ом, R₁ = 16 Ом, R₂ = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.

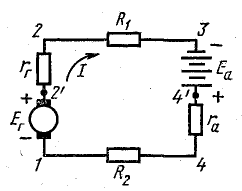
Рис. 4.4. К задаче 4.3

Эквивалентная э. д. с. цепи

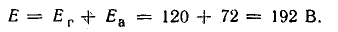
Эквивалентное внутреннее сопротивление

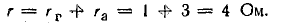
Эквивалентное сопротивление нагрузки

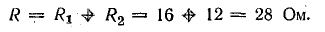
Ток в цепи

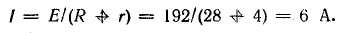
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора

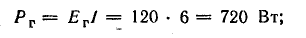
аккумуляторной батареи

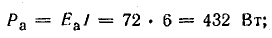
потерь внутри генератора

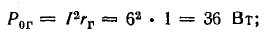
потерь внутри аккумуляторной батареи

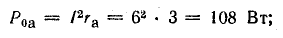
потребления в резисторе R₁

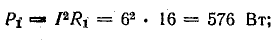
потребления в резисторе R₂
 
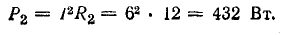
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)

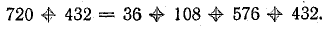
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V₁ = 0:

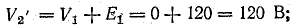
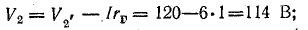
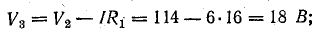
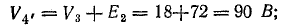
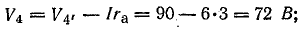
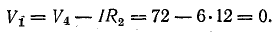
Потенциальная диаграмма показана на рис. 4.5.

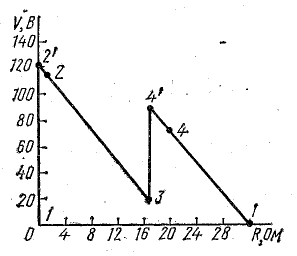
Рис. 4.5. Потенциальная диаграмма.

Разветвленная электрическая цепь с двумя узлами

Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.

Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.

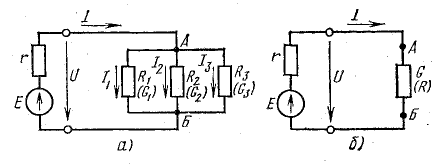
Рис. 4.7. Преобразование схемы с параллельным соединением приемников

Параллельное соединение пассивных элементов

Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R₁, R₂, R₃ и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа: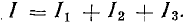
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:

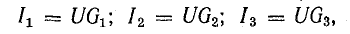
где


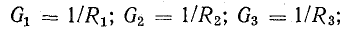
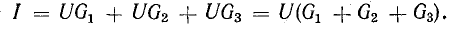
Разделим это уравнение на U:

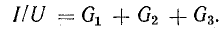
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:

Этот вывод можно распространить на любое число n параллельно соединенных приемников:

 

При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.

Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).

Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства

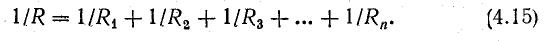
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле

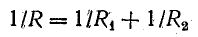
или

Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле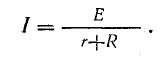

Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.

Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:

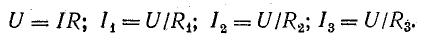
Параллельное соединение источников энергии

В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).

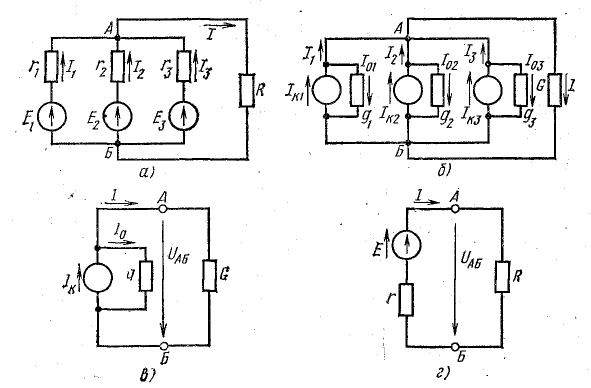
Рис. 4.8. Преобразование схемы с параллельным соединением источников

В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.

Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

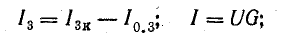
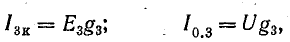
где U = U_аб — напряжение между узловыми точками А и Б.

По первому закону Кирхгофа, для узла А

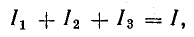
или

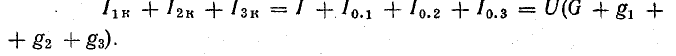
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания

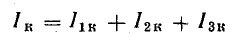
и внутренней проводимостью

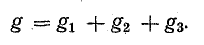
Для схемы рис. 4.8, в

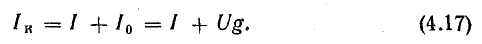
Напряжение между узлами

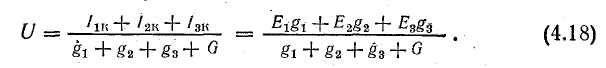
Токи в ветвях можно определить по следующим формулам:

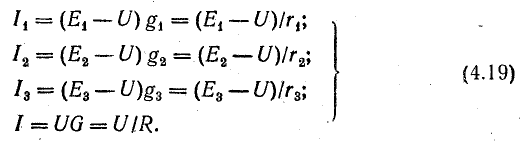
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.

Общий ток в этом случае определяется произведением тока одного источника I_n на число параллельно включенных источников:

Величина тока каждого источника ограничена его номинальным значением I_ном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.

От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:

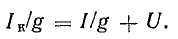
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то I_кr = Ir + U.
Но I_кr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.

Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.

Общий случай параллельного соединения источников и приемников электрической энергии

Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).

Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.

Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).

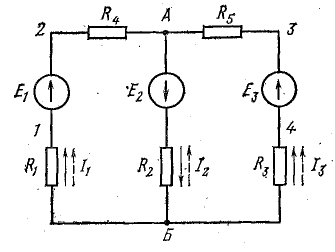
Рис. 4.9. Схема с двумя узлами

В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид

Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).

Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
 

Задача 4.8.

Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R₁ = 30 Ом, R₂ = 20 Ом, R₃ = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:


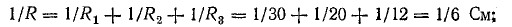
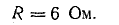
Ток в неразветвленной части цепи

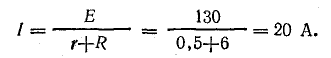
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:

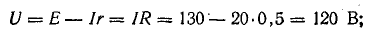
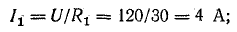
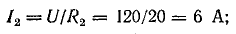
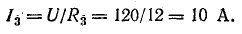
Проверим правильность определения токов по уравнению (4.1):

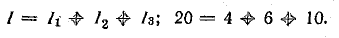
Мощность передачи энергии приемникам

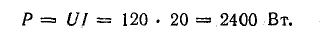
К. п. д. источника

 

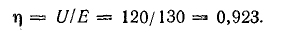
Задача 4.10. 

Для схемы, изображенной на рис. 4.7, а, известны: R₁ = 10 Ом; R₂ = 15 Ом; R₃ = 6 Ом, r = 0,5 Ом, l₃ = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:

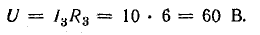
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:

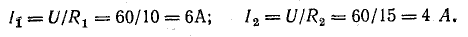
Ток в неразветвленной части цепи

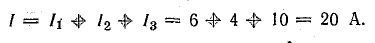
Э. д. с. источника

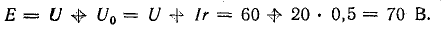
Мощность источника

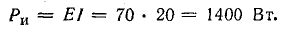
Мощность потребления энергии приемниками

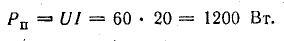
К. п. д. источника

 

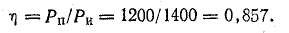
Задача 4.12.

Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E₁ = 120 В; E₂ = 80 В; E₃ = 60 В; r₁ = 0,5 Ом; r₂ = 0,4 Ом; r₃ = 0,2 Ом; R₁ = 2 Ом; R₂ = 15,6 Ом; R₃ = 12,4 Ом; R₄ = 7,5 Ом; R₅ = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем U_АБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:

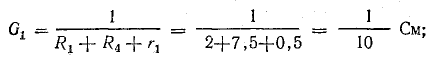
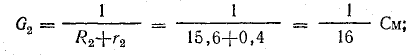
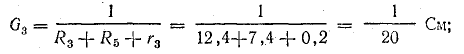
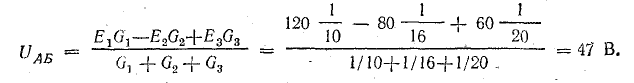
Токи в ветвях:

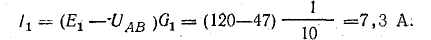
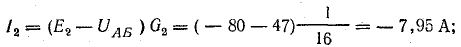
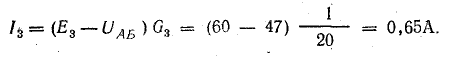
Токи l₁ и l₃ положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l₂ противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.

Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P_1.1 = E₁I₁ = 120 • 7,3 = 876 Вт; P_1.2 = Е₂I₂ = 80 • 7,95 = 636 Вт; Р_1.3 = E₃I₃ = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.

При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P_1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е₂ и I₂ сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.

Мощность потерь внутри источников: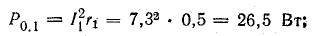
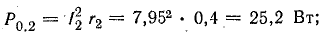
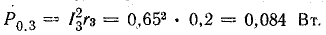
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:

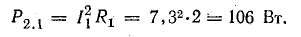
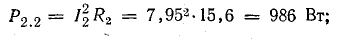
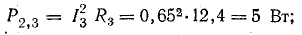
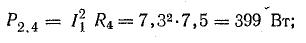
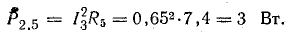
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.

Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)

Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
 

Определение эквивалентных сопротивлений

На схеме рис. 4.10, а сопротивления R₃ и R₄ включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I₃ = I₄. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму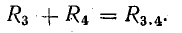
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R₂ и R_3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):

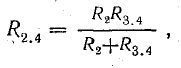
и получить более простую схему (рис. 4.10, в).

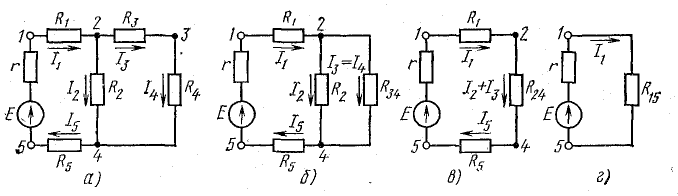
Рис. 4.10. К методу эквивалентных сопротивлений

В схеме рис. 4.10, в сопротивления R₁, К_2.4, К₅ соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).

Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.

Определение токов

В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что

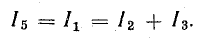
Кроме того, напряжение между точками 2 и 4

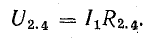
Зная это напряжение, легко определить токи I₂ и I₃ = I₄:

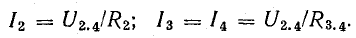
После определения токов I₁ и I₅ напряжение U_2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V₄ известным (например, равным нулю), а V₂ найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I₁ =I₅:

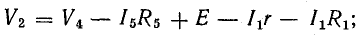
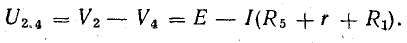
Метод преобразования треугольника и звезды сопротивлений

Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.

Треугольник и звезда сопротивлений

Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).

В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.

К узловым точкам a, b, c присоединен треугольник сопротивлений R_ab, R_bc, R_ca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений R_a, R_b, R_c (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.

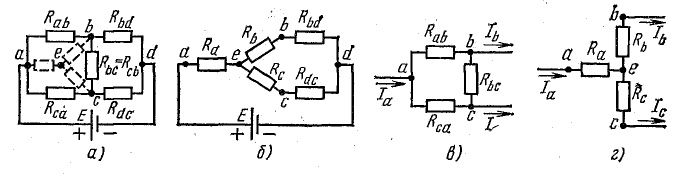
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
 
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления R_b и R_bd соединены между собой последовательно, так же как b сопротивления R_c и R_dc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
 

Преобразование треугольника сопротивлений в эквивалентную звезду

Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором I_a = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями R_bc и R_ab + R_ca
Общее сопротивление между этими точками

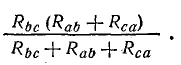
В схеме звезды между точками b и c включены последовательно сопротивления R_b и R_c. Общее сопротивление между этими точками R_b + R_c.
По условиям эквивалентности напряжение между точками b и c и токи I_b и I_c в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.

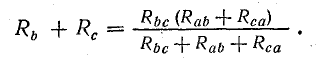
Полагая I_b =0, а затем I_c = 0, получим:

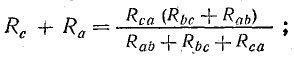
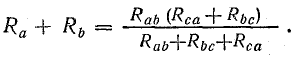
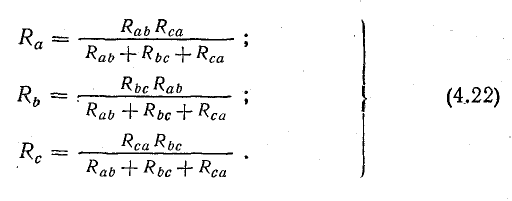
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:

 

Преобразование звезды сопротивлений в эквивалентный треугольник

Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.

При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:

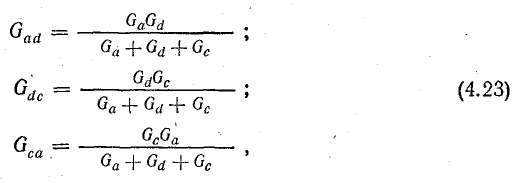
где G_ad; G_dc; G_ca — проводимости сторон треугольника; G_a; G_d; G_c — проводимости лучей звезды.

Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.

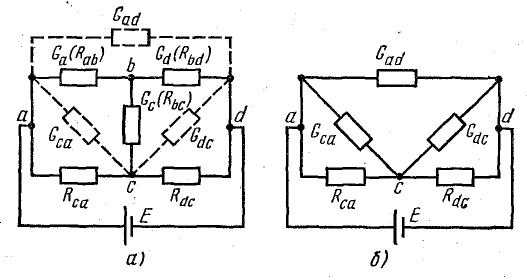
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник