Электрические цепи несинусоидального тока

Содержание:

Электрические цепи с несинусоидальными напряжениями и токами:

В этой главе рассматриваются электрические цепи, в которых напряжения или токи изменяются с течением времени по периодическим законам, отличным от синусоидального.

В электрической цепи с линейными элементами несинусоидальный ток возникает, если в ней действует несинусоидальное напряжение (э. д. с.).
Электромашинный генератор переменного тока может иметь кривую э. д. с., несколько отличную от синусоиды, вследствие несинусоидального распределения магнитной индукции под полюсом (см. рис. 22.4) или в связи с наличием пазов и зубцов в сердечниках статора и ротора.

Несинусоидальный ток и напряжение на отдельных участках цепи появляются и при синусоидальном напряжении источника, когда в цепи имеются элементы с нелинейной вольт-амперной характеристикой (см. рис. 24.2).

Ток в катушке с ферромагнитным сердечником получается несинусоидальным вследствие нелинейной зависимости между магнитным потоком и намагничивающим током (см. рис. 24.9).

Несинусоидальные напряжения, токи и их выражение

Несинусоидальные периодические функции, так же как и синусоидальные, наглядно изображаются в виде графиков. Для расчетов требуются аналитические выражения несинусоидальных функций.

Ряды Фурье

Аналитическое выражение несинусоидальный периодической функции осуществляется с помощью теоремы Фурье, согласно которой любая периодическая функция

Первая гармоническая составляющая имеет период, равный периоду несинусондальной кривой . Она называется первой или основной гармоникой.

Все другие гармонические составляющие имеют частоты, в целое число раз большие частоты первой гармоники. Эти гармоники называют высшими. На рис. 23.1, а-в показаны несинусоидальные э. д. с., содержащие две синусоидальные составляющие — первую и третью — при различной величине начальной фазы третьей гармоники:



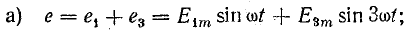
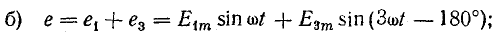
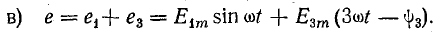
Выражение (23.1) можно преобразовать, применив известную из тригонометрии формулу синуса суммы двух углов:

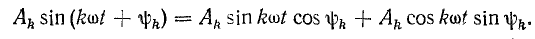
Обозначив постоянные величины

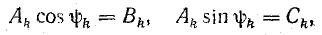
получим

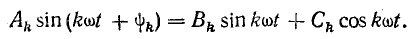
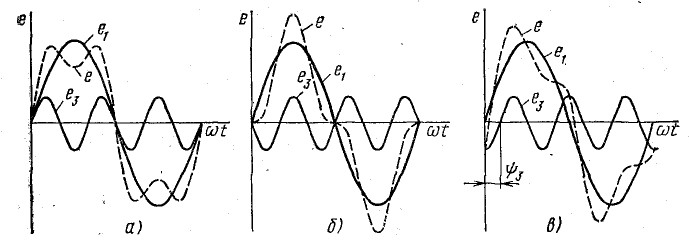
Рис. 23.1. Графики несинусоидальных э. д. с., содержащих первую и третью гармоники

Применяя подобную запись ко всем гармоническим составляющим, несинусоидальную функцию можно выразить так:


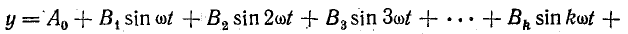
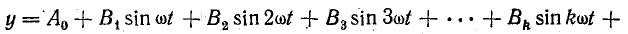
Особенность такой записи состоит в том, что гармоники составляют ряд синусов и ряд косинусов с нулевыми начальными фазами.

Коэффициенты ряда Фурье

Обратный переход от ряда (23.2) к ряду (23.1) нетрудно сделать, определив

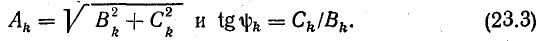
При определении угла 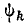нужно учитывать порознь знаки С_k и В_k, так как от них зависит величина угла. Например, при положительных С_k и В_k их отношение положительно, а угол лежит в первой четверти, при отрицательных С_k и В_k их отношение тоже положительно, но угол находится в третьей четверти.
При построении синусоид по оси абсцисс нужно откладывать начальную фазу k-й гармоники, пересчитав ее на масштаб основной гармоники, т. е. вместо 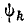отложить 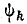/k.

Это следует из того, что градуировка оси абсцисс дается в масштабе первой гармоники, поэтому на отрезке 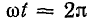укладывается k полных циклов k-й гармоники.
Коэффициенты А₀, В_k, С_k ряда (23.2) определяют при помощи следующих формул:



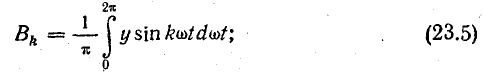
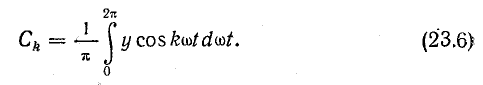
Если закон изменения ординат несинусоидальной кривой можно выразить в виде уравнения, то выражения (23.4) — (23.6) позволяют в большинстве случаев выполнить аналитически разложение ее в тригонометрический ряд вида (23.2) и далее, если нужно, перейти к ряду (23.1). Постоянная составляющая, как видно из формулы (23.4), является средним значением функции за ее период.
Таким образом, постоянная составляющая в тригонометрическом ряду отсутствует, если среднее за период значение функции равно нулю.

Графо-аналитический метод определения коэффициентов ряда Фурье

Коэффициенты ряда (23.2) можно определить графоаналитическим методом, который дает приближенные значения коэффициентов,, но зато является более общим, так как не требует аналитического выражения разлагаемой в ряд функции.

Периодическая кривая вычерчивается на графике (рис. 23.2). На протяжении отрезка, соответствующего периоду, на равных расстояниях 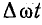друг от друга проводятся ординаты кривой.
Коэффициент А₀ — постоянная составляющая — определяется приближенным выражением

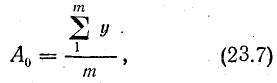
где 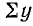— алгебраическая сумма всех ординат, взятая за период; m — число ординат.

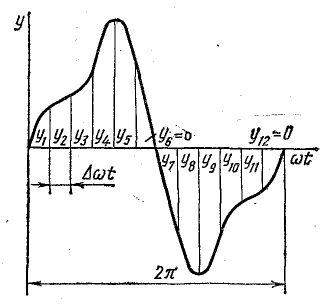
Рис. 23.2. К определению коэффициентов ряда графическим методом

Выражение (23.7) следует, из основного (23.4):

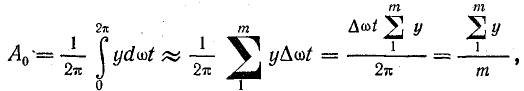
так как

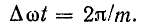
Результат определения А₀ тем точнее, чем меньше будет взят интервал 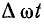между ординатами.
Аналогично определяются коэффициенты В_k и С_k на основании выражений (23.5) и (23.6):

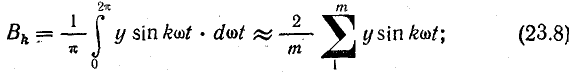
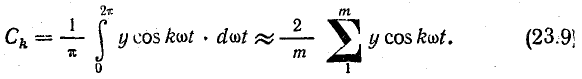
Задача 23.1.

Разложить в тригонометрический ряд графоаналитическим методом периодический ток, который получается в цепи рис. 23.3, а в результате однополупериодного выпрямления. Амплитуда тока 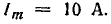 Нагрузка — активная.
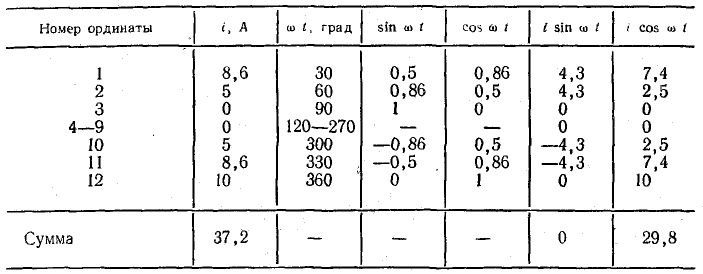
Решение. Построим график выпрямленного тока, разделим его на 12 частей с интервалом по оси абсцисс в 30° и проведем ординаты. Для определения постоянной составляющей I₀ и коэффициентов В₁ и С₁ составим табл. 23.1

Таблица 23.1

(график, подобный рис. 23.3, б, постройте в масштабе 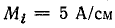на листе миллиметровой бумаги).

Ординаты найдены измерением по графику и занесены в таблицу. Все ординаты с 3 по 9 равны нулю. Другие графы таблицы заполняются по результатам расчетов при k = 1, так как определяются коэффициенты основной (первой) гармоники.

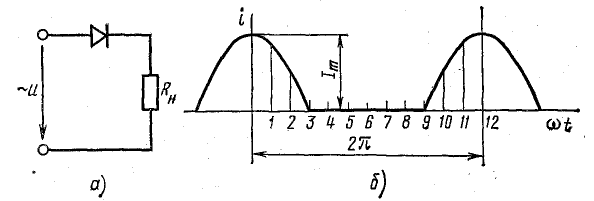
Рис. 23.3. К задаче 23.1

Согласно формуле (23.7), постоянная составляющая выпрямленного тока имеет величину

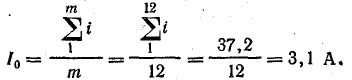
По формулам (23.8) и (23.9) найдем:


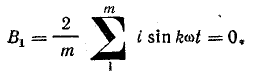
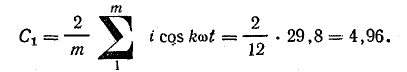
Для определения коэффициентов С_k (второй и далее гармоник) составляют аналогичные таблицы.
Для определения коэффициента С₂ составим табл. 23.2.

Таблица 23.2

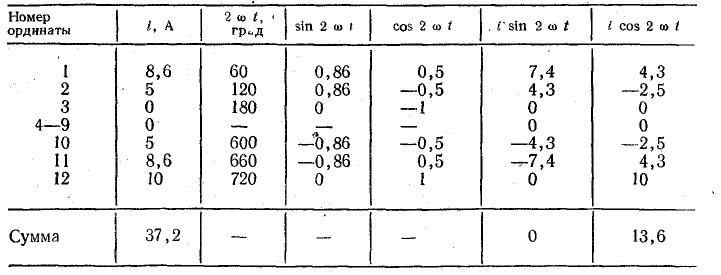
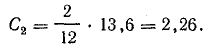
Для определения коэффициента С₃ составим табл. 23.3.

Таблица 23.3

 

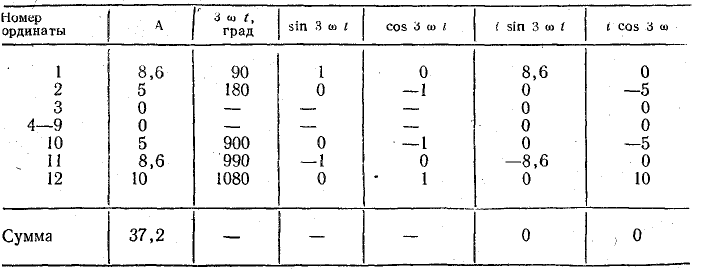
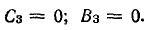
Таким образом, третья гармоника в составе ряда отсутствует.
В таком же порядке определены следующие коэффициенты: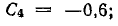   
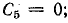
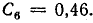
При определении коэффициентов можно заметить, что в составе ряда отсутствуют не только синусы, но и нечетные гармоники, кроме первой, а знаки высших гармоник чередуются.
Ряд заданной функции имеет вид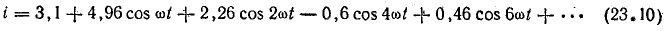

Симметричные несинусоидальные функции

Периодические функции, с которыми приходится встречаться в электротехнике, чаще всего имеют симметрию. Одни из них симметричны относительно оси абсцисс, другие — относительно оси ординат или начала координат.
Симметрия несинусоидальных кривых облегчает аналитическое их выражение.

Функция, симметричная относительно оси абсцисс

На рис. 23.4 показан график функции, симметричной относительно оси абсцисс. Для такого графика

При симметрии относительно оси абсцисс значения функции повторяются с обратным знаком через половину периода, поэтому отрицательная полуволна, сдвинутая на половину периода, является зеркальным отображением положительной полуволны.
Как будет показано далее (см. рис. 24.9), такую форму имеет кривая тока в катушке с ферромагнитным сердечником при синусоидальном напряжении.

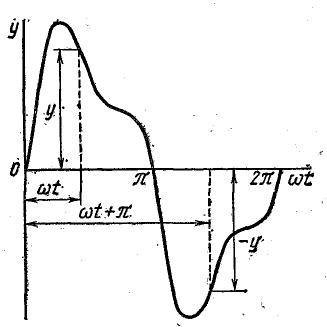
Рис. 23.4. График функции, симметричной относительно оси абсцисс

В составе тригонометрического ряда функции, подчиняющейся соотношению (23.11), отсутствуют постоянная составляющая и гармонические четного порядка. В этом нетрудно убедиться, если записать ряды вида (23.1) для функци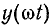й и :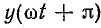

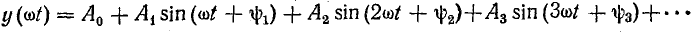
Функция 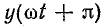отличается от  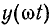тем, что все нечетные гармоники имеют отрицательный знак:


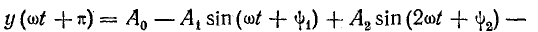
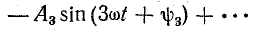
Согласно условию (23.11),
.
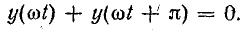Тогда

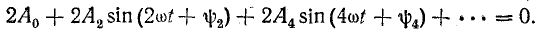
При любом 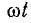это равенство возможно, если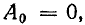 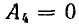и т. д.
Таким образом, кривая, симметричная относительно оси абсцисс, выражается тригонометрическим рядом следующего вида:


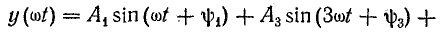
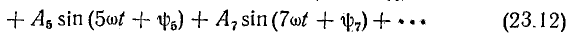
или

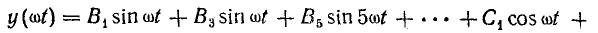
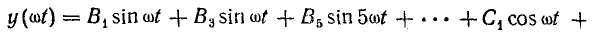
Функция, симметричная относительно оси ординат

Симметрию относительно оси ординат имеют кривые, у которых при изменении знака аргумента величина и знак функции не меняются (рис. 23.5):

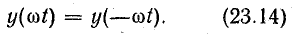
Такую симметрию имеет, например, ток в нагрузке схемы однополупериодного выпрямления (см. рис. 23.3).

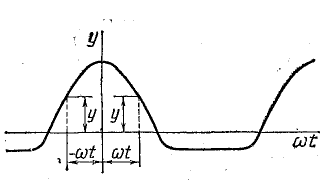
Рис. 23.5. График функции, симметричной относительно оси ординат

Функция, симметричная относительно оси ординат, не содержит синусов:
     
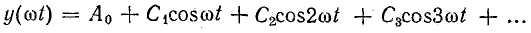
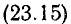
В этом можно убедиться без математического доказательства. Действительно, входящие в состав ряда (23.2) косинусы симметричны относительно оси ординат, а синусы несимметричны. Если функция в целом симметрична относительно оси ординат, то это возможно лишь при отсутствии синусов. Наличие же постоянной составляющей не нарушает симметрии такого характера.

Функция, симметричная относительно начала координат

Симметрия относительно начала координат (рис. 23.6) соответствует условию

В этом случае при изменении знака аргумента функция меняет знак, не меняя величины. Такая функция не содержит постоянной составляющей и косинусов.
Нетрудно заметить, что в данном случае в обеих половинах периода имеются две равные по величине ординаты с разными знаками. Поэтому среднее значение функции за период, или постоянная составляющая, равно нулю. Отсутствуют и несимметричные относительно начала координат косинусоидальные составляющие.

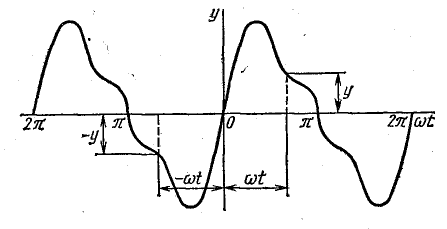
Рис. 23.6. График функции, симметричной относительно начала координат

Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом:

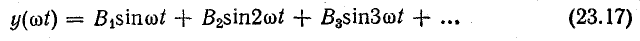
Задача 23.3.

Разложить в тригонометрический ряд аналитическим методом периодическую функцию, имеющую вид трапеции (рис. 23.7).
Решение. Заданная кривая симметрична относительно оси абсцисс. Поэтому ряд этой функции не имеет постоянной составляющей и четных гармоник. Кроме того, кривая симметрична относительно начала координат, поэтому в ее ряду не содержится косинусов. Таким образом, для написания ряда нужно определить коэффициент В_k.

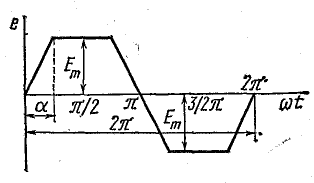
Рис. 23.7. К задаче 23.3

Выражение (23.5) для данного случая можно записать в таком виде:

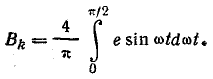
Это выражение записано с учетом симметрии трапеции, которая делится на четыре равных по площади участка. Каждый из них распространяется по оси абсцисс на π/2. Поэтому интегрирование ведется в пределах 1/4 периода и перед знаком интеграла ставится множитель 4.
На участке 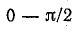  функция характеризуется разными уравнениями. В пределах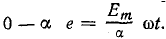
В пределах 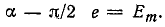 Тогда


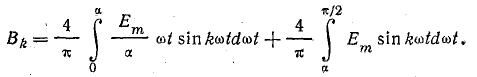
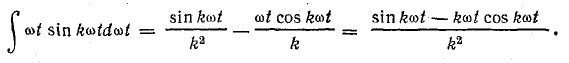
Тогда



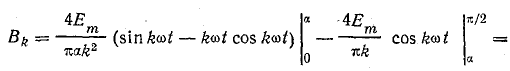
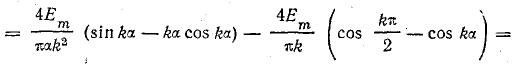
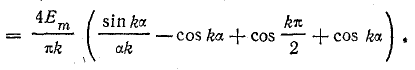
По условию симметрии, k — целое нечетное число, поэтому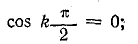 

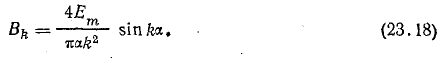
Ряд, выражающий трапецию, имеет вид

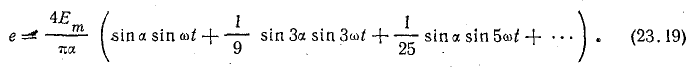
Из выражения (23.18) следует, что при 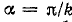ряд не содержит составляющих, кратных k. Например, если α = 60°, то не будет составляющих, кратных  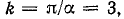т. е. третьей, девятой и т. д. Такая кривая мало отличается от синусоиды.

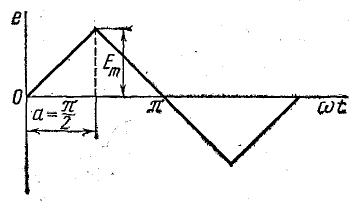
Рис. 23.8. К задаче 23.3

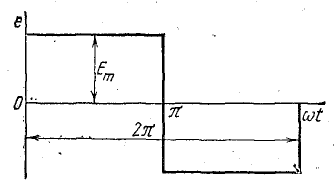
Рис. 23.9. К задаче 23.3

Рассмотрим частные случаи:
а) угол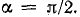
В этом случае график функции имеет вид, показанный на рис. 23.8, а ряд этой функции получается из выражения (23.19) после подстановки значения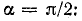

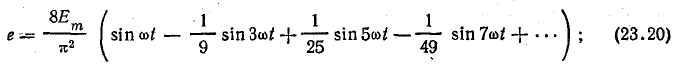
б) угол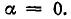  
В этом случае график функции имеет форму прямоугольника (рис. 23.9), а ряд ее находится также из выражения (23.19):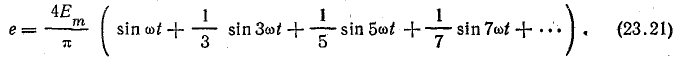

Действующая величина несинусоидального тока и мощность цепи

При расчете электрических цепей с несинусоидальными токами и напряжениями определяют величины токов, напряжений и мощности. При этом используют понятие о действующих величинах несинусоидальных токов и напряжений.

Действующая величина несинусоидального тока

Как известно, действующая величина синусоидального переменного тока численно равна такому постоянному току, при котором выделяется столько же тепла, сколько при переменном токе в одном и том же резисторе за одинаковое время, равное одному периоду Т. Из такого же условия определяют действующую величину переменного несинусоидального тока.
При этом нужно учесть, что несинусоидальный ток складывается из постоянной составляющей и ряда синусоидальных гармоник:


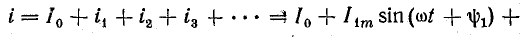
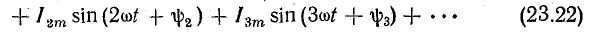
Очевидно, общее количество тепла, которое выделяется при несинусоидальном токе в некотором элементе цепи с сопротивлением R в течение одного периода T, будет равно сумме количеств тепла от всех его составляющих. В данном случае предполагается, что сопротивление R не зависит от частоты, т. е. поверхностный эффект не учитывается:

где Q — тепло, выделяемое за один период Т при несинусоидальном токе, действующая величина которого равна I:

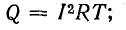
Q₀ — тепло, выделяемое за то же время при токе, равном постоянной составляющей:

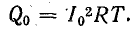
За время периода Т_k при токе, равном k-й составляющей, выделяется тепло

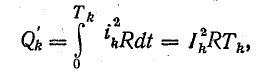
где I_k — действующая величина тока k-й гармоники.
За время, равное периоду основной гармоники, выделится в k раз больше тепла:

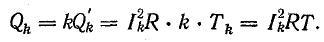
После подстановки в (23.23) получим

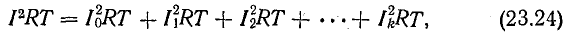
или

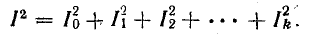
Отсюда следует, что действующая величина несинусоидального тока является средней квадратичной из постоянной составляющей и действующих величин синусоидальных составляющих этого тока:

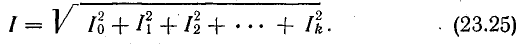
Аналогичное выражение можно получить и для действующей величины несинусоидального напряжения:

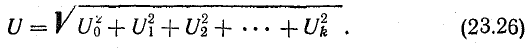
Действующие величины несинусоидальных токов и напряжений измеряются электроизмерительными приборами тепловой, электромагнитной и электродинамической систем.
Несинусоидальные периодические кривые характеризуются коэффициентом амплитуды и коэффициентом формы, а также коэффициентом искажения d.
Коэффициент искажения равен отношению действующих значений основной гармоники и всей функции

Для синусоиды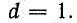
Для треугольной формы кривой (рис. 23.8) 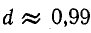, а для прямоугольной формы (рис. 23.9)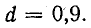

Мощность в электрической цепи при несинусоидальном токе

Выражение (23.24) дает основание для определения активной (средней за период Т) мощности в цепи при несинусоидальном токе.
Слагаемые в правой части этого выражения определяют энергию, соответствующую каждой составляющей тока и выделяемую в цепи за время Т.
После сокращения на Т получим уравнение активных мощностей

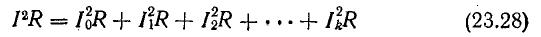
или

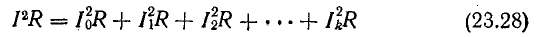
Активная мощность в цепи несинусоидального тока равна сумме активных мощностей, соответствующих постоянной составляющей и отдельным гармоникам. Этот вывод распространяется на любые цепи (линейные и нелинейные), так как формулу (23.29) можно получить из общего определения активной мощности как среднего значения мощности за период:

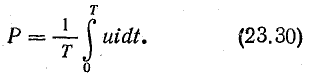
Задача 23.5.

Определить действующее значение несинусоидального тока, выраженного уравнением (23.10) [см. решение задачи 23.1].
Решение. Согласно решению задачи 23.1, составляющие заданного тока имеют следующие величины.
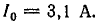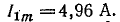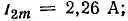
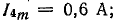
Постоянная составляющая  Амплитуда основной гармоники  Амплитуды высших гармоник:  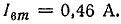 Действующие значения гармоник:


 
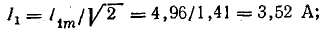
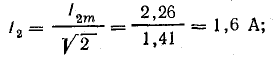
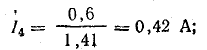
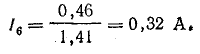
Действующая величина несинусоидального тока

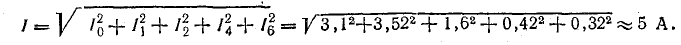
Определите действующую величину того же несинусоидального тока по разложению его в ряд, выполненному аналитическим способом (см. задачу 23.4):

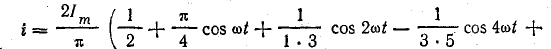
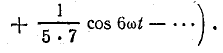
Расчет электрических цепей с несинусоидальными э. д .с. и токами

Цели и задачи расчета электрических цепей с несинусоидальными токами не отличаются от тех, которые были указаны для цепей постоянного тока и цепей с синусоидальными напряжениями и токами.

Применение принципа наложения

Расчет линейной электрической цепи с несинусоидальными э. д. с. выполняется на основе принципа наложения.

Применение принципа наложения обусловлено возможностью представления несинусоидальной э. д. с. в виде суммы постоянной и синусоидальных составляющих:

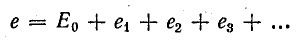
Источник несинусоидальной э. д. с. можно представить как последовательное соединение источника постоянной э. д.с. и источников синусоидальных э. д. с. с соответствующими частотами.

Рассматривая действие каждого источника в отдельности, можно определить составляющие тока во всех участках цепи, выполняя расчет известными методами.

Мгновенная величина общего тока в любом участке цепи равна алгебраической сумме мгновенных токов от каждого источника: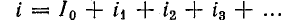
Следовательно, расчет линейной цепи с несинусоидальной э. д. с. сводится к решению нескольких задач: определение одной постоянной составляющей и ряда синусоидальных составляющих тока, число которых равно числу синусоидальных составляющих э. д. с.

Решая эти задачи, нужно помнить, что реактивные сопротивления зависят от частоты. Поэтому для каждой гармонической составляющей нужно определять сопротивления цепи.

Сопротивление цепи

Индуктивное и емкостное сопротивления для первой гармоники находят по известным формулам.

Те же сопротивления для k-й гармоники отличаются от сопротивлений для первой в k раз:


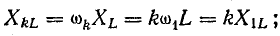
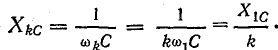
Активное сопротивление из-за поверхностного эффекта тоже зависит от частоты. Но для невысоких частот и малых сечений проводов активное сопротивление можно считать постоянным, равным сопротивлению постоянного тока.

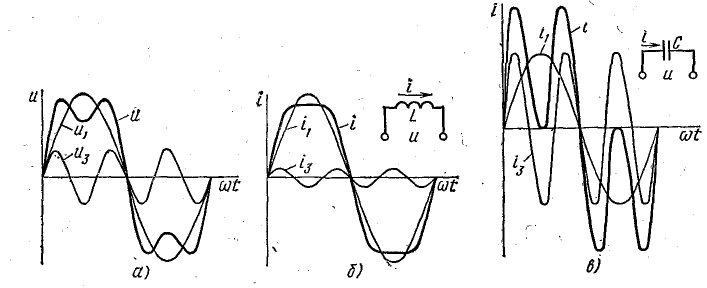
Рис. 23.11. Графики напряжения и тока, содержащие первую и третью гармоники, в цепях с индуктивностью и емкостью

Реактивное сопротивление конденсатора уменьшается с ростом частоты, поэтому даже при напряжении, близком к синусоидальному, составляющие тока высших гармоник могут достигать значительных величин. Благодаря этому кривая тока при емкостной нагрузке больше отличается от синусоиды, чем кривая напряжения. При индуктивной нагрузке кривая тока ближе к синусоиде, чем кривая напряжения, так как с ростом частоты индуктивное сопротивление растет и высшие гармоники проявляются слабее. Это положение иллюстрируется рис. 23.11, на котором изображены графики напряжения (а) и тока — в цепи с индуктивностью (б) и в цепи с емкостью (в). Одинаковое для обеих цепей несинусоидальное напряжение содержит первую и третью гармоники.

Сопротивления для первой гармоники тока приняты также одинаковыми (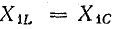, т. е. 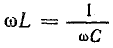). Сопротивление для третьей гармоники в цепи:
с индуктивностью

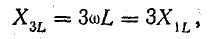
с емкостью

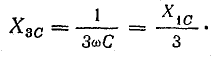
При таком соотношении сопротивлений первые гармоники тока в обеих цепях одинаковы, третья гармоника тока в цепи с индуктивностью меньше третьей гармоники тока в цепи с емкостью в девять раз.

Замечание о применении векторных диаграмм

При определении синусоидальных составляющих тока можно пользоваться символическим методом и строить векторные диаграммы. В то же время общий ток нельзя определять сложением комплексов или векторов составляющих разных частот.

Такое сложение синусоидальных величин возможно лишь тогда, когда они имеют одинаковую частоту. В этом случае соответствующие векторы вращаются с одинаковой частотой, а их взаимное расположение на чертеже не меняется. Векторы, изображающие синусоидальные величины разных частот, вращаются с разными угловыми скоростями, поэтому их взаимное расположение на чертеже непрерывно изменяется и сложение таких векторов невозможно.

Иногда для упрощения расчетов несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными, имеющими такие же действующие величины.

Благодаря такой замене можно использовать векторные диаграммы и полученные на их основе расчетные формулы. Например, активную мощность можно представить произведением действующих величин несинусоидальных напряжения, тока и коэффициента мощности :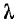

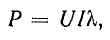
причем 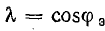, где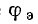 — условный угол сдвига фаз между эквивалентными синусоидами напряжения и тока.

Задача 23.7.

Катушка с активным сопротивлением R = 18 Ом и индуктивностью L = 0,0383 Гн соединена последовательно с конденсатором С = 88,5 мкФ (рис. 23.12). На зажимах цепи действует напряжение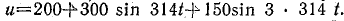
Найти выражение мгновенных значений и действующие значения тока, напряжений на катушке и конденсаторе. Определить активную мощность в цепи.

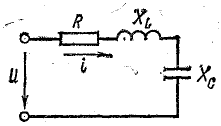
Рис. 23.12. к задаче 23.7
Решение. Сопротивление цепи для постоянной составляющей тока равно бесконечности, так как в цепи имеется конденсатор. Постоянная составляющая тока равна нулю: I₀ = 0. Сопротивления цепи для первой гармоники:



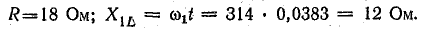
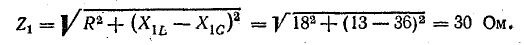
Реактивное сопротивление току первой гармоники имеет емкостный характер:

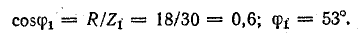
Амплитуда тока первой гармоники

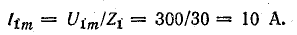
Сопротивление цепи для третьей гармоники


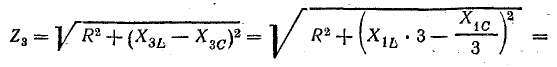
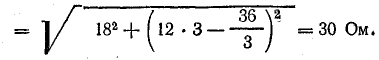
Реактивное сопротивление току третьей гармоники имеет индуктивный характер:

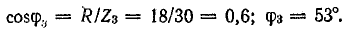
Амплитуда тока третьей гармоники

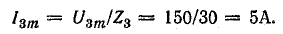
Действующие величины токов:
первой и третьей гармоник
    
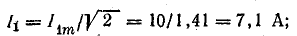
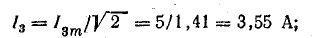
общего тока

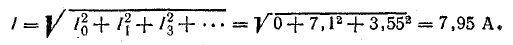
Уравнение общего тока

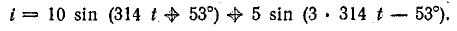
Для определения напряжения на катушке найдем сопротивления катушки токам первой и третьей гармоник:




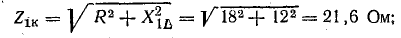
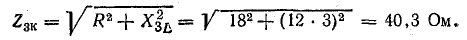
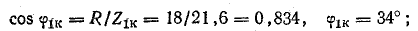
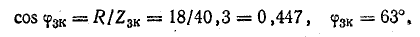
Амплитуды первой и третьей гармоник напряжения на катушке:


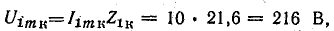
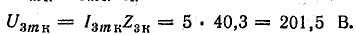
Уравнение напряжения на катушке


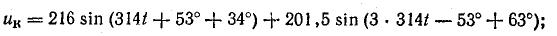
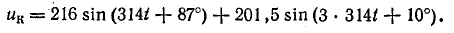
Напряжение на конденсаторе состоит из постоянной составляющей, первой и третьей гармоник. Постоянная составляющая напряжения на конденсаторе равна постоянной составляющей напряжения сети, как напряжение между точками разрыва цепи:

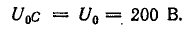
Первая гармоника

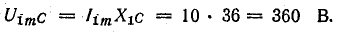
Третья гармоника

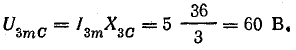
Уравнение напряжения на конденсаторе


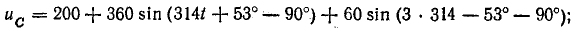
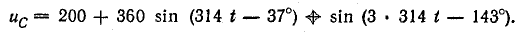
Действующие напряжения на катушке и конденсаторе:


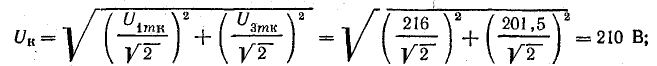
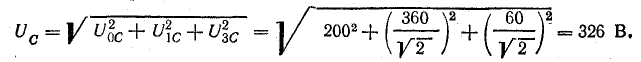
Активная мощность в цепи

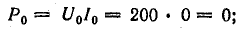
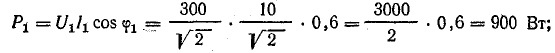
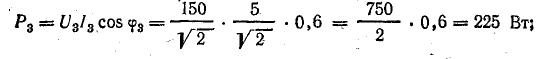
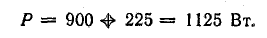
Высшие гармоники в трехфазных цепях

Трехфазные цепи в отношении высших гармоник напряжений и токов имеют некоторые особенности.

Рассмотрим известные схемы соединения трехфазных систем при несинусоидальных напряжениях. При этом будем полагать, что напряжения не содержат постоянных составляющих и четных гармоник, т. е. рассматриваются кривые напряжения, симметричные относительно оси абсцисс, которые в практике встречаются наиболее часто.

Симметричные составляющие гармоник

Симметричная трехфазная система напряжений, как известно, характеризуется тем, что кривые напряжений во всех фазах по форме одинаковы, но сдвинуты на одну треть периода (2π/3).

Основную гармонику напряжений можно выразить системой трех уравнений

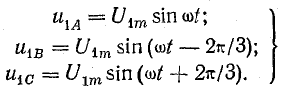
Система уравнений для k-х гармоник фазного напряжения отличается от предыдущей тем, что аргумент синусоидальной функции увеличен в k раз:


.
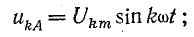
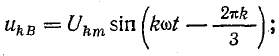
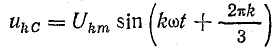Рассмотрим сначала гармоники, кратные трем, т. е. положим 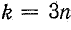, где n — целое число:



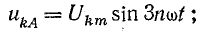
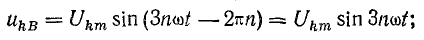
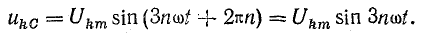
Напряжения во всех фазах одинаковы и совпадают по фазе, так как сдвиг на полный период (или целое число периодов 2πn) равнозначен отсутствию сдвига.
Гармоники, кратные трем, т. е. 3, 6, 9, 12 и т. д., образуют симметричную систему нулевой последовательности.
На рис. 23.13, а гармоники напряжения, кратные трем, показаны тремя одинаковыми векторами, совпадающими по направлению.
Если 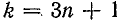, то напряжение 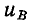отстает по фазе от 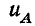на угол 2π/3, а 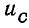опережает  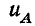на такой же угол.
Например, четвертые гармоники фазных напряжений 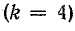выражаются уравнениями



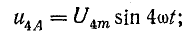
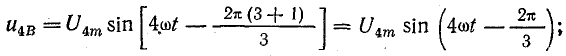
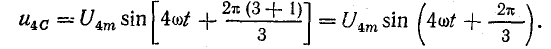
Следовательно, гармоники I, 4, 7, 10, 13 и т. д. образуют симметричную систему прямой последовательности.

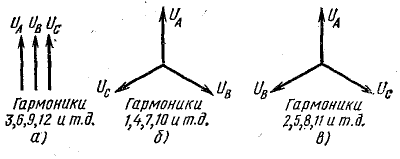
Рис. 23.13. Симметричные составляющие системы несинусоидальных напряжений в трехфазных цепях

На рис. 23.13, б показана векторная диаграмма напряжений этих гармоник. Векторы диаграммы нужно представлять вращающимися против движения часовой стрелки с угловой скоростью 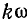, при этом порядок следования векторов прямой: за вектором U_А следует вектор U_B, а затем U_C.
Полагая 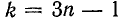, нетрудно установить, что напряжение  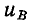опережает 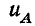по фазе на угол 2π/3, а 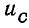отстает от 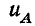на такой же угол. Например, пятые  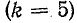гармоники фазных напряжений имеют уравнения:



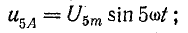
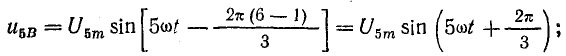
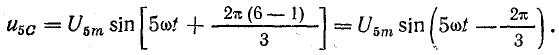
Гармоники 2, 5, 8, 11, 14 и т. д. образуют симметричную систему обратной последовательности. Порядок следования векторов диаграммы на рис. 23.13, в при вращении их против движения часовой стрелки обратный: за вектором U_A следует U_C и далее U_B (следование векторов в прямом порядке 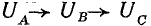соответствует вращению их в обратном направлении по движению часовой стрелки).

Если напряжения фаз имеют одинаковые постоянные составляющие, то в совокупности их можно рассматривать как составляющую нулевой последовательности при частоте, равной нулю.

Соединение звездой

При соединении обмоток источника звездой (рис. 23.14) линейные напряжения равны разностям фазных напряжений двух смежных фаз.

Совпадая по фазе, гармоники фазных напряжений, кратные трем (k = 3; 6; 9; ...), при вычитании дадут нуль. Поэтому в линейных напряжениях гармоники, кратные трем, отсутствуют.
По этой причине при несинусоидальных напряжениях

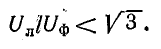
Действительно,

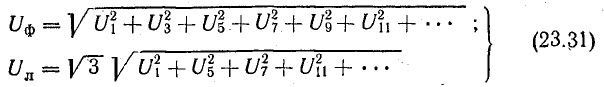
Рассмотрим симметричную нагрузку, соединенную звездой, отметим два случая.

1. При наличии нулевого провода третьи гармоники фазных токов складываются, образуя ток в нулевом проводе: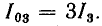
Это также относится и к высшим гармоникам, кратным трем. Все остальные гармоники, образуя системы прямой или обратной последовательности, в сумме дают нуль.

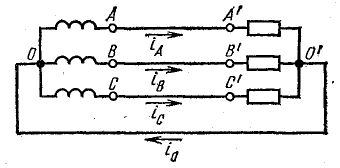
Рис. 23.14. К вопросу о высших гармониках в трехфазной цепи при соединении звездой

Таким образом, при симметричной нагрузке в нулевом проводе имеется ток, равный утроенной сумме токов высших гармоник нулевой последовательности:

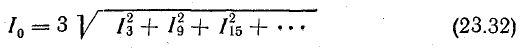
2. При отсутствии нулевого провода сумма фазных токов в любом случае равна нулю, поэтому в составе фазных токов гармоники, кратные трем, должны отсутствовать. Следовательно, фазные напряжения на нагрузке не могут содержать гармоник, кратных трем.

Для токов нулевой последовательности отсутствие нулевого провода означает разрыв в цепи на участке между нулевыми точками источника и приемника. Таким образом, между нулевыми точками образуется напряжение (смещение нейтрали) каждой гармоники, кратной трем, причем величина смещения равна величине этой гармоники в фазном напряжении источника.
Учитывая все гармоники, вызывающие смещение, получим напряжение между нулевыми точками источника и приемника даже при симметричной нагрузке:

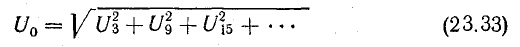
Такое смещение нейтрали, связанное с действием гармоник тока, кратных трем, может наблюдаться в электрических сетях 6-35 кВ с изолированной нейтралью.

Соединение треугольником

Обмотки генератора или трансформатора, соединенные треугольником (рис. 23.15), образуют замкнутый контур. Результирующая э. д. с. трех фаз в этом контуре равна нулю, если э. д. с. каждой фазы не имеет гармоник, кратных трем, так как трехфазная система э. д. с. каждой гармоники является симметричной системой прямой или обратной последовательности.

При наличии в э. д. с. обмоток гармоник, кратных трем, последние образуют системы нулевой последовательности, поэтому результирующая э. д. с. гармоники, кратной трем, будет равна утроенной э. д.с. одной фазы.
Например, результирующая э. д. с. третьей гармоники Е₃' = 3Е₃.

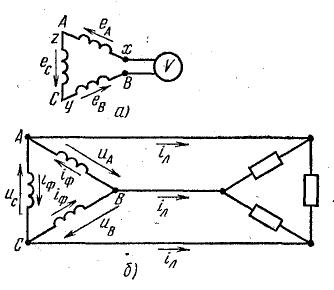
Рис. 23.15. К вопросу о высших гармониках в трехфазной цепи при соединении треугольником

Вольтметр, включенный последовательно в контур обмоток источника (рис. 23.15, а), покажет общее напряжение

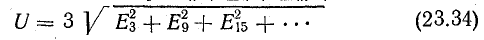
В замкнутом треугольнике обмоток источника без нагрузки (внешняя цепь источника разомкнута) результирующая э. д. с. гармоник, кратных трем, вызывает ток, который условно назовем внутренним или уравнительным (рис. 23.15, б).
В обмотках нагруженного источника кроме тока нагрузки существует тот же уравнительный ток гармоник, кратных трем.
Уравнительный ток вызывает в обмотках источника падения напряжения, уравновешивающие э. д. с. этих гармоник.
Результирующая э. д. с. гармоник, не кратных трем, является фазным (и линейным) напряжением источника при отсутствии нагрузки

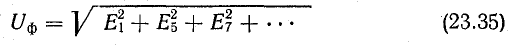
Отсутствие в напряжении источника гармоник, кратных трем, является причиной отсутствия этих гармоник в токах внешней цепи.
Таким образом, фазный ток генератора

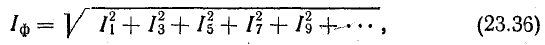
линейный ток во внешней цепи

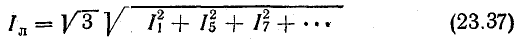
Нетрудно заметить, что

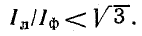
Уравнительный ток в обмотках источника вызывает дополнительный их нагрев, поэтому соединение треугольником обмоток генераторов обычно не применяется.

Задача 23.9.

Э. д. с. в фазе вторичной обмотки трехфазного трансформатора содержит 1, 3, 5 и 7-ю гармоники с амплитудами 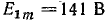; ; 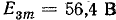;  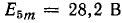 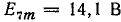и начальными фазами, равными нулю. Определить показания вольтметров, включенных, как в схемах рис. 23.16, а, б, в. Вольтметр показывает действующее напряжение.

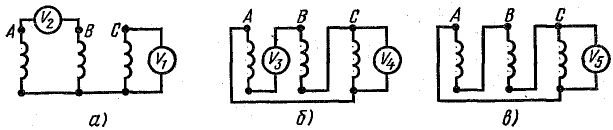
Рис. 23.16. К задаче 23.9

Решение. Уравнение э. д. с. в фазе

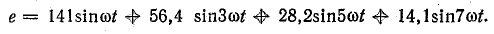
Действующие значения составляющих э.д. е.:
 
  
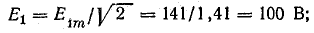
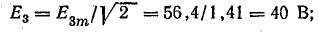
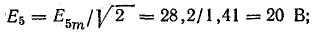
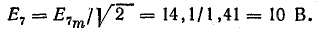
Вольтметр V₁ включен на фазное напряжение при соединении звездой без нагрузки:

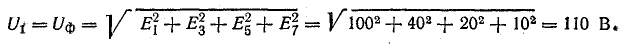
Вольтметр V₂ при тех же условиях измеряет линейное напряжение, в составе которого отсутствует третья гармоника:

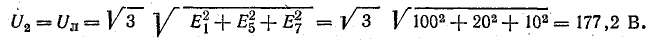
При соединении треугольником по схеме рис. 23.16, б контур из обмоток трансформатора замкнут через вольтметр V₃, т. е. через большое сопротивление.
Практически сумма всех составляющих напряжения трех обмоток приложена к вольтметру. Но гармоники 1, 5, 7, не кратные трем, в сумме дают нуль.
Гармоники 3, кратные трем, образуют системы нулевой последовательности, поэтому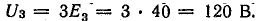
Определите показания вольтметров V₄ и V₅.

Задача 23.10.

Определить показания амперметров в схемах рис. 23.17 (при замкнутом и разомкнутом рубильнике Р), если в обмотках трансформатора действует симметричная система э. д. с., заданных в предыдущей задаче, а сопротивление нагрузки в фазе выражается комплексом 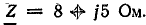 Сопротивление фазы генератора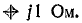
Решение. При соединении звездой по схеме рис. 23.17, а с замкнутым рубильником, т. е. с нулевым проводом, амперметр А показывает сумму токов нулевой последовательности. В данном случае это будет утроенный ток третьей гармоники, так как нагрузка симметрична:
.
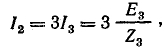где Z₃ — полное сопротивление фазы для третьей гармоники:
    

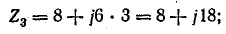
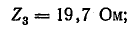
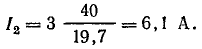
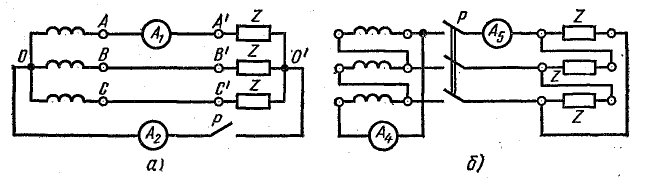
Рис. 23.17. К задаче 23.10

Амперметр А₁ покажет действующее значение общего тока в фазе:

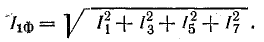
Определить действующие токи всех гармоник, учитывая изменение реактивного сопротивления в зависимости от частоты, и показание амперметра А₁.
При разомкнутом рубильнике показание амперметра A₂ = 0.
Ток в фазе нужно определить, выполнив для каждой гармоники расчет цепи известными методами.
Для 1, 5, 7-й гармоник цепь представляет собой симметричную трехфазную систему, поэтому достаточно определить ток в фазе по формуле

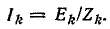
Третьи гармоники фазных напряжений образуют систему нулевой последовательности. В данном случае следует определить напряжение между нулевыми точками U₀. Для третьей гармоники отсутствие нулевого провода соответствует разрыву цепи, поэтому 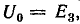 а ток третьей гармоники в фазе равен нулю.
При соединении треугольником по схеме 23.17, б и при разомкнутом рубильнике амперметр А₄ показывает ток в контуре из обмоток трансформатора, создаваемый третьей гармоникой э. д. с. всех фаз.
При замкнутом рубильнике амперметр А₄ показывает фазный, а амперметр А₅ — линейный ток в трехфазной системе. Эти токи определите по формулам (23.36) и (23.37), предварительно найдя действующие токи каждой гармоники.