
ЭДС индукции в движущемся проводнике - формулы и определение с примерами
ЭДС индукции в движущемся проводнике:
На заряженную частицу, движущуюся в магнитном поле индукцией 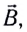
Рассмотрим проводник, находящийся в магнитном поле. Свободные заряды внутри проводника участвуют в тепловом движении. Вследствие хаотичности
теплового движения средняя скорость перемещения и среднее смещение частиц равны нулю. Следовательно, при тепловом движении заряженных частиц внутри проводника среднее значение силы Лоренца также равно нулю. При поступательном движении проводника как целого ситуация меняется, поскольку наряду с тепловым (беспорядочным) движением свободные заряды участвуют в направленном движении вместе с проводником.
Рассмотрим движение проводника длиной l со скоростью 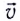 перпендикулярно магнитному полю индукцией
перпендикулярно магнитному полю индукцией 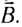 Поскольку свободные электроны движутся вместе с проводником со скоростью
Поскольку свободные электроны движутся вместе с проводником со скоростью 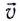 (рис. 164), то под действием силы Лоренца
(рис. 164), то под действием силы Лоренца 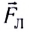 они будут смещаться вдоль проводника к его концу D. Направление силы Лоренца можно определить по правилу левой руки с учетом знака заряда электрона.
они будут смещаться вдоль проводника к его концу D. Направление силы Лоренца можно определить по правилу левой руки с учетом знака заряда электрона.
Вследствие этого на торцах D и А проводника появятся, соответственно, отрицательные и положительные заряды, которые создадут электрическое поле, а значит, и некоторую разность потенциалов  между торцами проводника.
между торцами проводника.
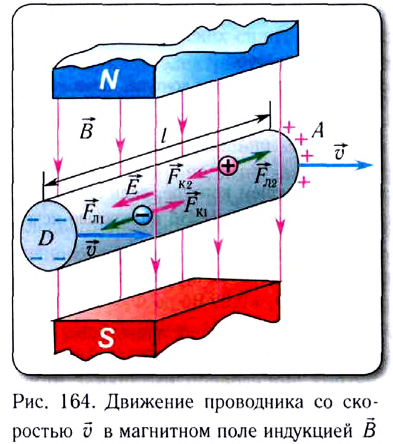
Процесс разделения зарядов (поляризации проводника) будет продолжаться до тех пор, пока сила, действующая на любой свободный электрон со стороны электрического поля 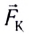 (см. рис. 164), не уравновесит силу Лоренца
(см. рис. 164), не уравновесит силу Лоренца 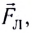 действующую на электрон со стороны магнитного поля.
действующую на электрон со стороны магнитного поля.
С учетом выражения для силы Кулона, действующей на каждый электрон 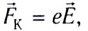 где
где 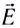 — напряженность созданного электрического поля, и силы Лоренца
— напряженность созданного электрического поля, и силы Лоренца 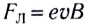 можно записать:
можно записать:
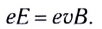
Откуда
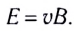
Под действием сил Кулона и Лоренца заряды будут находиться в равновесии, и дальнейшее их разделение прекратится. По всей длине проводника установится однородное электрическое поле. Между концами проводника (в разомкнутой цепи) длиной l появится разность потенциалов
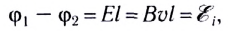 которая является частным случаем возникновения ЭДС электромагнитной индукции.
которая является частным случаем возникновения ЭДС электромагнитной индукции.
Таким образом, при движении проводника длиной l со скоростью 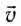 в постоянном магнитном поле индукцией
в постоянном магнитном поле индукцией 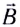 в нем возникает ЭДС индукции
в нем возникает ЭДС индукции
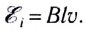
Причиной появления этой ЭДС является сила Лоренца, действующая на свободные электроны в движущемся проводнике.
Подчеркнем, что полная работа силы Лоренца в движущемся проводнике равна нулю. Продольная составляющая силы Лоренца 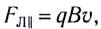 действующая на заряды, совершает работу
действующая на заряды, совершает работу 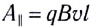 по их разделению (рис. 165).
по их разделению (рис. 165).
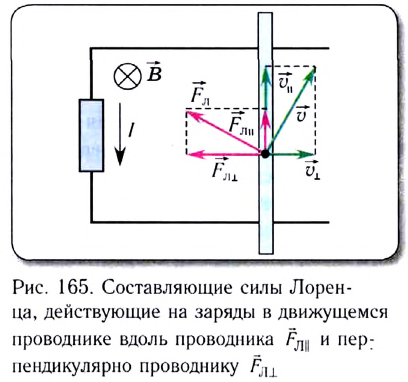
Поперечная составляющая 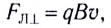 направленная противоположно скорости движения проводника, совершает работу
направленная противоположно скорости движения проводника, совершает работу 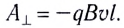 Полная работа силы Лоренца (сумма этих работ) равна нулю
Полная работа силы Лоренца (сумма этих работ) равна нулю 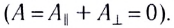 Вследствие того что работа поперечной составляющей силы Лоренца отрицательна, при движении проводника в магнитном поле происходит его торможение. Поэтому для движения проводника с постоянной скоростью на него необходимо действовать постоянной внешней силой, равной по модулю поперечной составляющей силы Лоренца.
Вследствие того что работа поперечной составляющей силы Лоренца отрицательна, при движении проводника в магнитном поле происходит его торможение. Поэтому для движения проводника с постоянной скоростью на него необходимо действовать постоянной внешней силой, равной по модулю поперечной составляющей силы Лоренца.
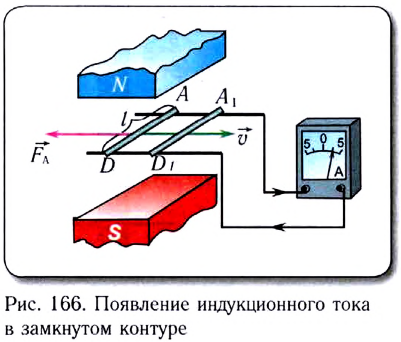
Если проводник замкнуть расположенным вне магнитного поля проводом (рис. 166), то по этому проводу от точки D к точке А электроны будут перемещаться под действием ЭДС электромагнитной индукции.
Существование ЭДС индукции приводит к появлению в замкнутом контуре индукционного тока. Таким образом, электроны в проводнике движутся от точки А к точке D против сил электрического поля под действием силы Лоренца, а от точки D к точке А по проводу (во внешней цепи) их движение происходит под действием сил электрического поля.
Когда проводник длиной l с индукционным током силой I движется в магнитном поле индукцией 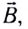 то на него со стороны поля действует сила Ампера, модуль которой
то на него со стороны поля действует сила Ампера, модуль которой 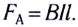 Для определения направления этой силы применим правило левой руки (рис. 167).
Для определения направления этой силы применим правило левой руки (рис. 167).
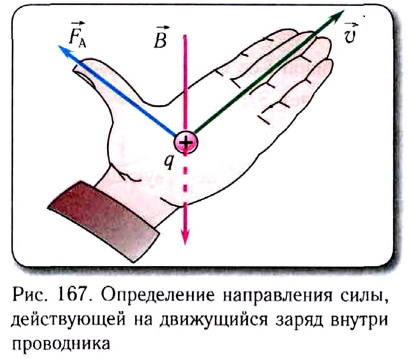
Направление силы противоположно направлению движения про
водника. Следовательно, индукционный ток, взаимодействуя с магнитным полем, создает силу, тормозящую движение проводника. Таким образом, для движения проводника необходима внешняя сила, совершающая работу против силы Ампера. Индукционный ток нагревает проводник, по которому он проходит. Выделяющаяся в виде тепла энергия поступает в цепь благодаря работе, которую совершает внешняя сила, двигая проводник против сил поля.
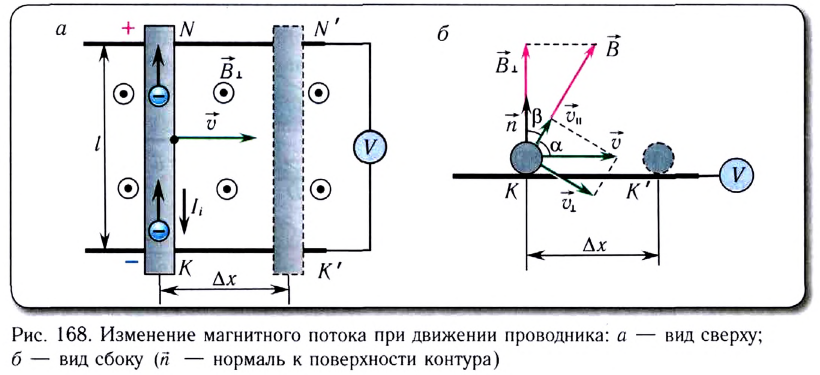
Если проводник, расположенный перпендикулярно линиям индукции магнитного поля, движется со скоростью 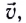 направленной под углом
направленной под углом 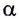 к линиям индукции (рис. 168, а), то ее можно разложить на две составляющие — параллельную
к линиям индукции (рис. 168, а), то ее можно разложить на две составляющие — параллельную 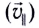 и перпендикулярную
и перпендикулярную 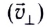 направлению магнитного поля (рис. 168, б):
направлению магнитного поля (рис. 168, б):
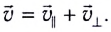
При движении проводника вдоль линии индукции в нем не возникает ЭДС индукции, поэтому вклад в 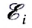 вносит только перпендикулярная составляющая скорости
вносит только перпендикулярная составляющая скорости 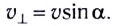 Вследствие этого выражение для ЭДС индукции в общем виде представляется соотношением
Вследствие этого выражение для ЭДС индукции в общем виде представляется соотношением
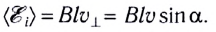
Таким образом, в общем случае необходимо учитывать угол между направлением скорости движения проводника (скорости электронов) и вектором индукции магнитного поля (как это делалось для силы Лоренца).
Вернемся к рассмотрению ЭДС электромагнитной индукции, возникающей в проводнике, движущемся равномерно и прямолинейно в магнитном поле. Поскольку скорость определяется, как 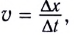 то выражение для ЭДС можно представить в виде
то выражение для ЭДС можно представить в виде
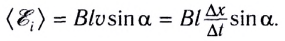
Учитывая, что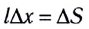 — площадь прямоугольника KNN'K', охватываемая проводником за промежуток времени
— площадь прямоугольника KNN'K', охватываемая проводником за промежуток времени 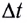 (см. рис. 168, а), можем записать:
(см. рис. 168, а), можем записать:
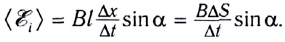
С учетом определения магнитного потока полученное выражение для ЭДС индукции можно представить в виде (см. рис. 168, б):
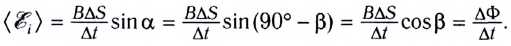
Здесь 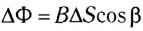 — изменение магнитного потока через контур за промежуток времени
— изменение магнитного потока через контур за промежуток времени 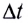 (число пересеченных проводником линий индукции магнитного поля).
(число пересеченных проводником линий индукции магнитного поля).
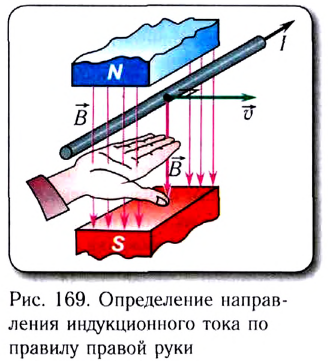
Направление индукционного тока в контуре с перемещающимся проводником может быть установлено с помощью правила правой руки (рис. 169):
если ладонь правой руки расположить так, чтобы вектор индукции 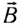 магнитного поля входил в ладонь, а отставленный на 90° большой палец совпадал с направлением скорости движения проводника, то четыре вытянутых пальца укажут направление индукционного тока.
магнитного поля входил в ладонь, а отставленный на 90° большой палец совпадал с направлением скорости движения проводника, то четыре вытянутых пальца укажут направление индукционного тока.
Таким образом, явление электромагнитной индукции связано с изменением магнитного потока через контур вне зависимости от характера причин, обусловливающих это изменение. ЭДС электромагнитной индукции прямо пропорциональна скорости изменения магнитного потока, т. е. изменению магнитного потока через контур в единицу времени.
Подчеркнем еще раз, что изменение магнитного потока через контур возникает при изменении:
- индукции
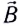 магнитного поля;
магнитного поля; - площади S контура;
- ориентации контура в магнитном поле (угла
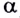 ).
).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |