Единичная окружность - с примерами решения

Содержание:

На рисунке 2 изображены колебания маятника и показан график функции, описывающей смещение маятника от положения равновесия в зависимости от времени. Изучение процесса колебания маятника, а также многих других процессов в физике (механические, электромагнитные колебания, волны и т. д.) приводит к необходимости рассматривать тригонометрические функции действительного аргумента.

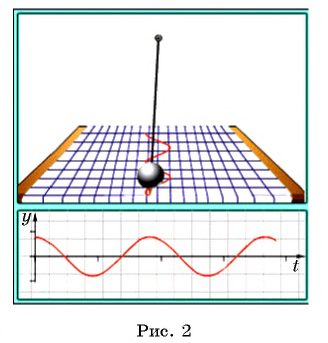
Для изучения тригонометрических функций используется понятие единичной окружности.

Единичная окружность в тригонометрии

Единичную окружность называют также координатной окружностью.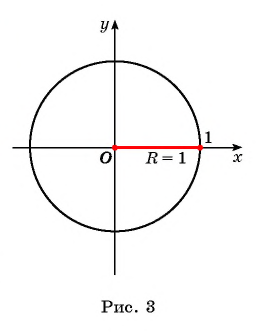

Определение единичной окружности

Определение:

Окружность на координатной плоскости единичного радиуса с центром в начале координат (рис. 3) называется единичной окружностью.

Для того чтобы задать координатную окружность, нужно указать:

• начало отсчета — точку
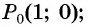
• направление движения точки по окружности (против часовой стрелки — положительное, а по часовой стрелке — отрицательное (рис. 4)).

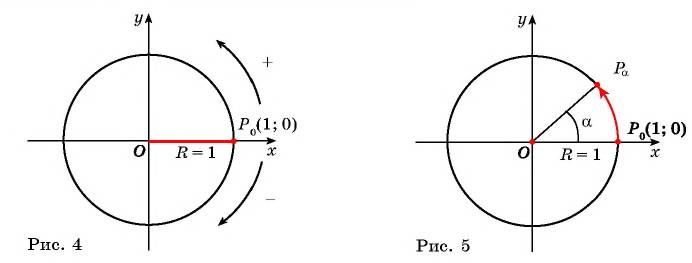
Точки на окружности будем получать путем поворота точки 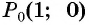единичной окружности вокруг начала координат на заданный угол.

Точка 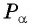(рис. 5) получена поворотом

• точки 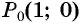(указывается, какая точка поворачивается)
• вокруг начала координат (указывается центр поворота)
• на угол 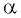(указывается, на какой угол выполняется поворот — угол поворота).

Таким образом, при повороте точки 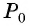вокруг начала координат на угол 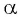в заданном направлении получается точка 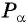единичной окружности.

Пример №1

Построить на единичной окружности точку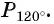

Решение:

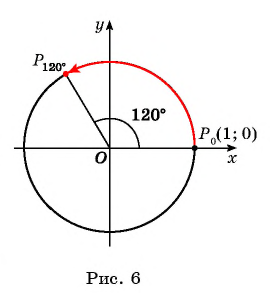
Точку 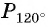получаем поворотом против часовой стрелки точки 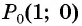вокруг начала координат на угол 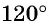(рис. 6).

Пример №2

Построить на единичной окружности точку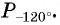

Решение:

Точку 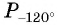получаем поворотом по часовой стрелке точки 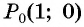вокруг начала координат на угол 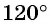(рис. 7).

Пример №3

Построить на единичной окружности точку:

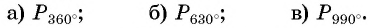
Решение:

а) Так как поворот на 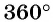соответствует одному полному обороту, то необходимо выполнить поворот точки 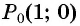против часовой стрелки на 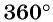(полный оборот). Точка 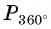совпадет с точкой 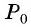(рис. 8, а).

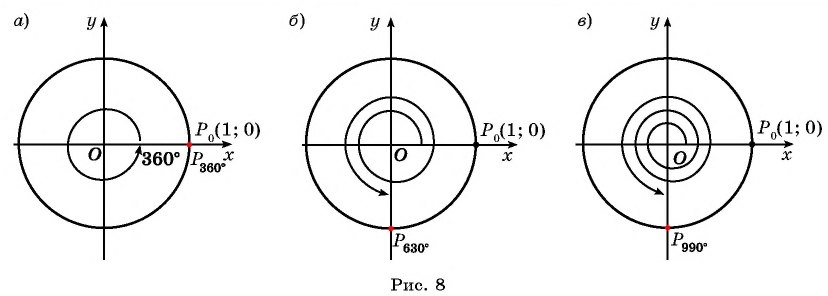
б) Так как 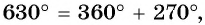то необходимо выполнить один полный оборот и еще поворот точки 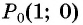вокруг начала координат против часовой стрелки на угол 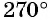(рис. 8, б).

в) Так как 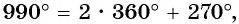то необходимо выполнить два полных оборота и еще поворот точки 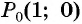вокруг начала координат против часовой стрелки на угол 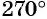(рис. 8, в).

Пример №4

Построить на единичной окружности точку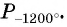

Решение:

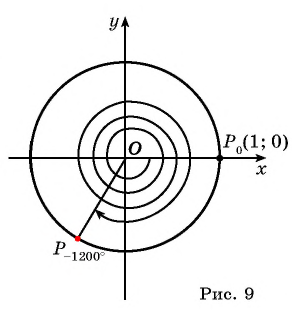
Так как 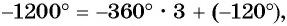то необходимо выполнить три полных оборота и еще поворот точки 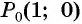вокруг начала координат по часовой стрелке на угол 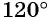(рис. 9).

Радианное измерение углов

По формуле длины окружности 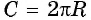получим, что длина единичной окружности 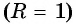равна

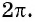
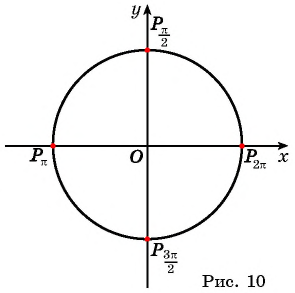
На единичной окружности (рис. 10) легко отметить точки 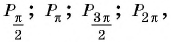соответствующие углам поворота 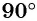(четверть окружности), 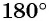(половина окружности), 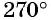(три четверти окружности), 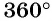(вся окружность).

Числа 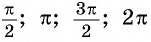- это радианная мера углов, градусная мера которых соответственно равна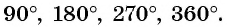

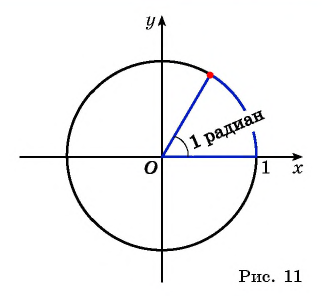
Угол в 1 радиан (от лат. radius — луч, радиус) — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.

На рисунке 11 отмечена точка единичной окружности, соответствующая углу в 1 радиан. Длина дуги единичной окружности, соответствующей углу в 1 радиан, равна 1.

Так как 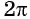радиан соответствует 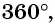то градусная мера угла в 1 радиан равна:

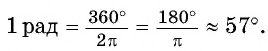
Сокращенное обозначение радиана «рад» чаще всего опускают.

Чтобы выразить радианную меру угла 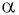в градусной, число 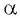умножить на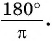

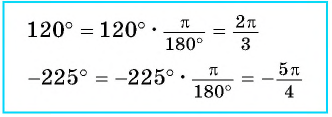
Например,

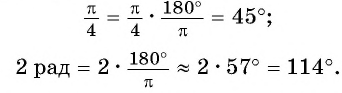
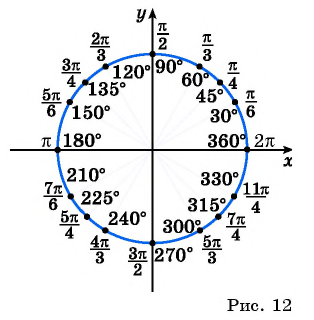
На рисунке 12 показано соответствие между градусной и радианной мерой некоторых углов.

• Заказать решение задач по высшей математике

Пример №5

Построить на единичной окружности точку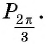

Решение:

Точку 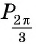получаем поворотом против часовой стрелки точки 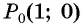вокруг начала координат на угол 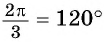(рис. 13).

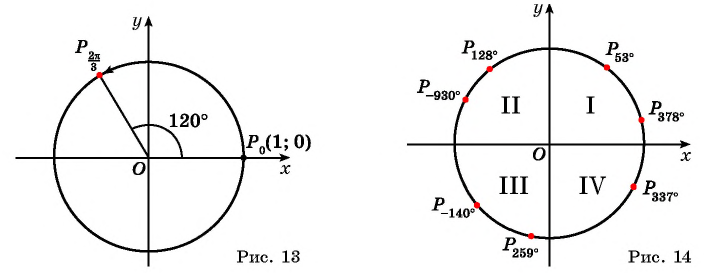
В зависимости от того, в какую четверть координатной плоскости попадает точка 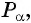говорят, что в такой же четверти находится угол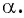

Например, углы 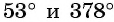находятся в первой четверти, углы 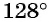и 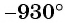находятся во второй четверти, углы 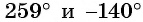находятся в третьей четверти, а угол 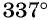находится в четвертой четверти (рис. 14).

Углы 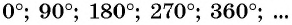соответствуют границам четвертей.

Пример №6

Определите, в какой четверти находится угол 3 рад.

Решение:

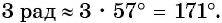Так как 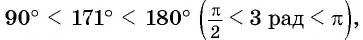то данный угол находится во второй четверти.

Примеры заданий и их решения

Пример №7

На единичной окружности отметьте точку, получаемую поворотом точки 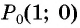вокруг начала координат на угол:

Решение.

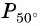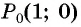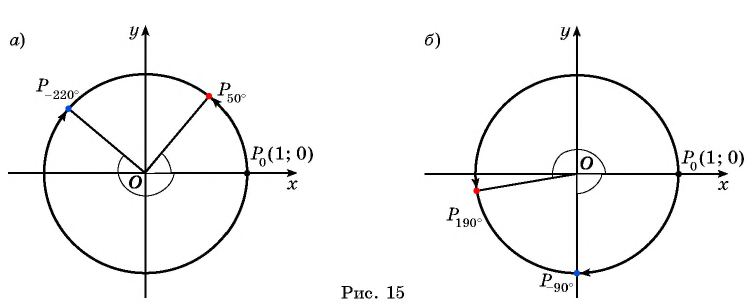
а) Точку получаем поворотом против часовой стрелки точки вокруг начала координат на угол 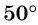(рис. 15, а).

б) Точку 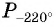получаем поворотом по часовой стрелке точки 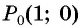вокруг начала координат на угол 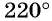(см. рис. 15, а).

в) Точку 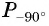получаем поворотом по часовой стрелке точки 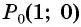вокруг начала координат на угол 90° (рис. 15, б).

г) Точку 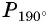получаем поворотом против часовой стрелки точки 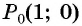вокруг начала координат на угол 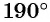(см. рис. 15, б).

Пример №8

Покажите, что точки:

— единичной окружности совпадают.

Решение:

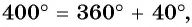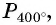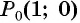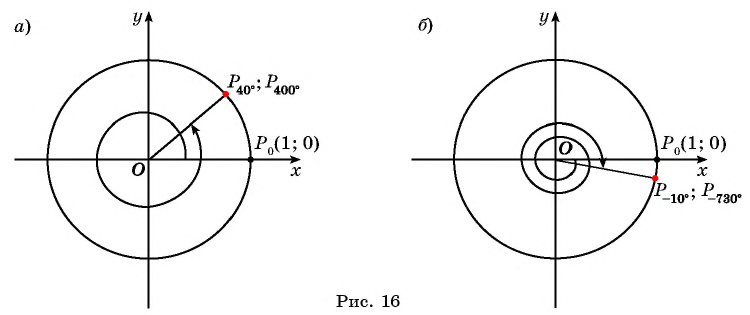
а) Поскольку то, для того чтобы получить точку нужно выполнить один полный оборот и еще поворот точки вокруг начала координат против часовой стрелки на угол 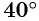(рис. 16, а).

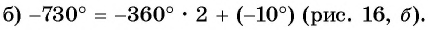
Пример №9

На единичной окружности отметьте точку, получаемую поворотом точки 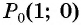вокруг начала координат на угол:

Решение:

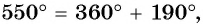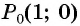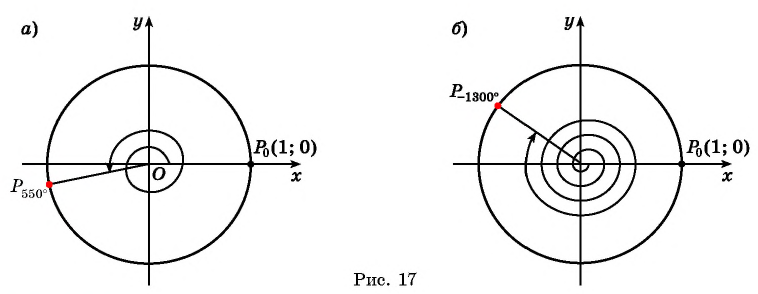
а) Так как то выполним один полный оборот и еще поворот точки вокруг начала координат против часовой стрелки на угол 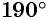(рис. 17, а).

б) Так как 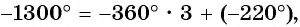то выполним три полных оборота и еще поворот точки 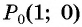вокруг начала координат по часовой стрелке на угол 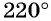(рис. 17, б).

Пример №10

Запишите все углы 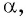для которых точка 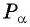совпадает с точкой:

Решение:

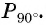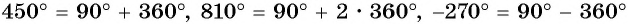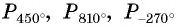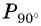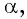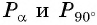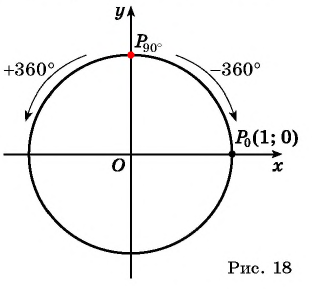
а) Отметим на единичной окружности точку Так как, например, и т. п., то точки единичной окружности совпадают с точкой единичной окружности. Очевидно, что существует бесконечно много углов для которых точки единичной окружности совпадают. Эти углы могут быть получены в результате поворота точки 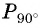на целое число полных оборотов по или против часовой стрелки (рис. 18), таким образом,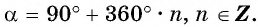

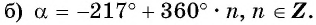
Пример №11

На единичной окружности отметьте точку, получаемую поворотом точки 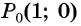вокруг начала координат на угол:

Решение:

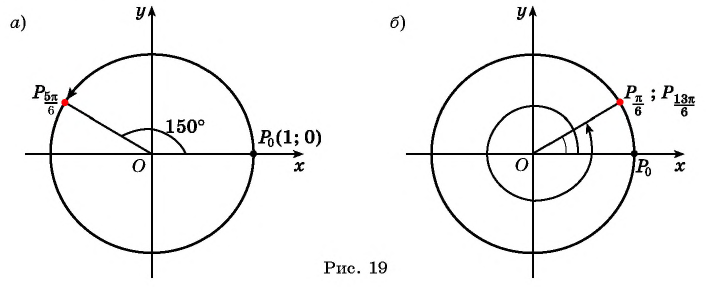
а) Так как 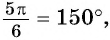то выполним поворот точки 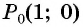вокруг начала координат на угол 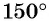(рис. 19, а).

б) Поскольку 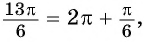то точка 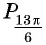совпадает с точкой 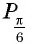(рис. 19, б).