Движение жидкостей - формулы и определение с примерами

Движение жидкостей:

Как уже отмечалось, раздел механики, изучающий движение жидкостей и газов, а также взаимодействие движущихся жидкостей и газов с твердыми телами, называется гидро- и аэродинамикой.

Наблюдая за течением воды в реке или движением атмосферного воздуха, можно убедиться в сложном характере движения. Спокойное течение воды в реке в одних местах соседствует с вихревым движением в других. Если слегка открыть кран, вода вытекает струйкой, которая не изменяет свое положение в пространстве, если полностью открыть кран — форма струи изменяется, происходит разбиение ее на отдельные струи и капли. Порывы ветра сменяются относительно спокойным движением воздуха. Поэтому гидро- и аэродинамика — сложная в математическом и физическом смысле наука.

Во-первых, необходимо научиться описывать движение каждой частицы жидкости и, во-вторых, установить законы, которым подчиняется это движение.

Как и движение твердых тел, движение жидкостей и газов происходит под действием сил. Мы уже знаем, что это силы давления и тяжести. Кроме того, необходимо еще учитывать наличие сил внутреннего трения, или вязкости.

Вязкостью называется свойство жидкости или газа оказывать сопротивление относительному перемещению своих частей.

Как мы впоследствии покажем, давление в различных точках потока жидкости или газа различно. Поэтому выделенный объем жидкости или газа подвергается различному сжатию при движении. Если сжимаемость жидкости мала, то у газов она существенна. Как известно, при сжатии газа его температура увеличивается. Таким образом, без учета тепловых явлений, происходящих в движущемся газе, нельзя построить теорию движения, используя только законы механики.

Однако, если скорости движения жидкостей и газов малые, значительно меньше скорости звука, то тепловыми явлениями можно пренебречь. Если еще пренебречь силами внутреннего трения, то мы получим модель идеальной жидкости. Итак, модель идеальной жидкости состоит в том, что не учитывают вязкость жидкости и ее сжимаемость. Мы в основном будем рассматривать явления в идеальной жидкости.

Движение жидкости, при котором отдельные слои скользят друг относительно друга, не перемешиваясь, называется ламинарным (слоистым) течением. Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений, называется турбулентным (вихревым).

Ламинарным является течение воды в спокойных реках. Оно наиболее изучено, и мы ограничимся рассмотрением ламинарного течения.

Однако наиболее распространенным является турбулентное движение. Примерами турбулентного движения могут служить беспорядочное движение дыма из заводских труб (рис. 183), завихрения воды в реках за сваями мостов или большими камнями (рис. 184), образование смерчей и т.д.

Ламинарное течение переходит в турбулентное движение при увеличении скорости жидкости. Течение жидкости удобно наблюдать с помощью прибора, изображенного на рисунке 185. Он состоит из широкой стеклянной трубки, соединенной через боковой отросток с водопроводом. В торец через пробку введена тонкая трубка, соединенная с сосудом, в который налита подкрашенная жидкость. Пока скорость течения воды невелика, струйка подкрашенной жидкости движется, не распадаясь, вместе с водой. Это ламинарное течение.
Постепенно открывая водопроводный кран, мы можем так увеличить скорость движения воды, что возникает турбулентное течение. Жидкость завихряется, и окрашенная струйка размывается в широкую ленту с неровными краями (рис. 186).

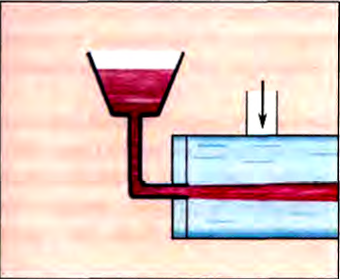Рис. 185

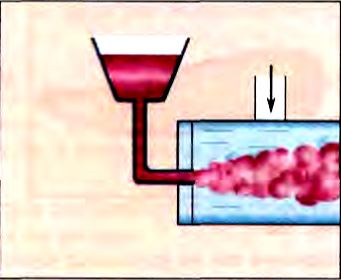Рис. 186

Турбулентное движение в реальных жидкостях очень сложно. До сих пор нет полной теории его, хотя проблемы турбулентности изучаются уже более 150 лет.

При описании движения жидкостей поступают следующим образом. Выделяют в жидкости малые объемы (частицы) и одновременно определяют скорости этих элементов во всем объеме жидкости. Наглядное представление о движении жидкости можно получить с помощью линий тока. Они строятся следующим образом. Выделим в потоке жидкости некоторую частицу. Она имеет в данный момент скорость 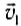. Отступим немного, перейдем к следующей частице, которая имеет скорость 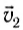в тот же момент времени. Поступая аналогичным образом, соединим частицы кривой так, чтобы касательная к ней была параллельна скорости частиц (рис. 187). Построенная таким образом линия и есть линия тока. Существенно отметить, что линии тока строятся для некоторого фиксированного момента времени. На ней находятся частицы.
скорости которых направлены по касательной к линии тока.

Если во всех точках пространства линии тока не меняют своего положения со временем, то такое течение жидкости называется стационарным (установившимся). При стационарном течении частицы, приходящие в данную точку пространства в различные моменты времени, имеют одну и ту же скорость. В этом случае линия тока совпадает с траекторией частиц.

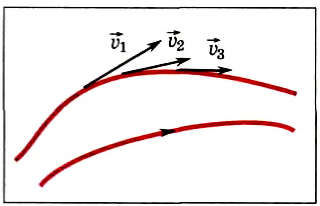
Рис. 187

Если линия тока меняет свое положение в пространстве со временем, то такое движение жидкости называется нестационарным.

Объем жидкости, ограниченный линиями тока, называется трубкой тока (рис. 188). Скорости частиц жидкости в каждой точке боковой поверхности трубки направлены по касательной к ней. Поэтому при своем
движении они не пересекают стенок трубки.

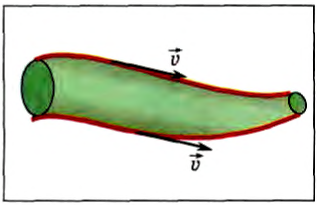
Рис. 188

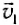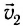Выделим в жидкости тонкую трубку тока, чтобы в каждом поперечном сечении скорости частиц жидкости можно было считать одинаковыми. Рассмотрим два сечения трубки тока с площадями S₁ и S₂ (рис. 189). Обозначим через и соответствующие скорости течения жидкости.

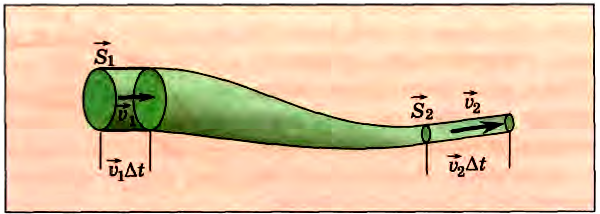
Рис. 189

За малый промежуток времени Δt через первое сечение проходит жидкость. масса которой равна p₁S₁υ₁Δt, а через второе —p₂S₂υ₂Δt. Здесь р₁ и р₂ — плотности жидкости в первом и втором сечениях. Поскольку через боковую поверхность трубки тока жидкость не поступает, то массы жидкости, протекающие через оба сечения, должны быть равны:
p₁S₁υ₁Δt= p₂S₂υ₂Δt.

Мы выбрали сечения трубки тока произвольно. Следовательно, для любого сечения трубки тока величина pSυ одинаковая. Таким образом, мы пришли к уравнению неразрывности.

При стационарном течении жидкости величина pSυ пастоянна для любого сечения трубки тока: 
pSυ = const.    (1)

Если жидкость несжимаема (p = const), то уравнение неразрывности для любого сечения трубки тока примет вид:
Sυ = const.    (2)

Уравнение неразрывности выражает закон сохранения массы. Согласно этому уравнению скорость жидкости в узких местах больше, чем в широких.

Уравнения (1) и (2) можно использовать и для широких трубок тока, если под V понимать среднюю скорость жидкости по сечению.

Главные выводы:

1. Ламинарным (слоистым) движением жидкости называется такое движение, при котором отдельные слои ее скользят друг относительно друга, не перемешиваясь.
2. Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений, называется турбулентным (вихревым).
3. Линия тока — это воображаемая линия, проведенная в жидкости в некоторый момент времени так, что все частицы жидкости, находящиеся на ней, имеют скорость, направленную по касательной к этой линии.
4. При стационарном течении жидкости для любого сечения тонкой трубки тока справедливо уравнение неразрывности.