
Движение в гравитационном поле в физике - формулы и определение с примерами
Содержание:
Движение в гравитационном поле:
Вы в 7-ом классе узнали о том, что Земля создает вокруг себя постоянное поле притяжения и с помощью этого поля притягивает к себе все тела. Значит, на любое движение на Земле оказывает свое влияние поле притяжения. Представим, что с вершины горы брошено какое-либо тело в горизонтальном направлении со скоростью 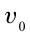
Если скорость тела увеличить, то оно упадет в точке 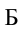 или
или 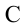 . Начиная с некоторой определенной скорости тела не падают на Землю, а начинают вращаться вокруг Земли. Такое тело становится искусственным спутником Земли. Движение искусственного спутника является движением в поле притяжения. Почему спутник не падает на Землю? При каких скоростях
. Начиная с некоторой определенной скорости тела не падают на Землю, а начинают вращаться вокруг Земли. Такое тело становится искусственным спутником Земли. Движение искусственного спутника является движением в поле притяжения. Почему спутник не падает на Землю? При каких скоростях
это происходит? Сначала рассмотрим силы, действующие на спутник. На спутник постоянно действует сила притяжения Земли. Чтобы снизить сопротивление воздуха, спутник нужно поднять в самые верхние слои атмосферы.
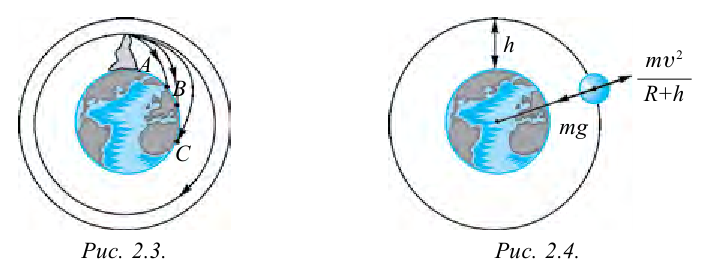
На высоте 300 – 400 км от поверхности Земли сопротивление воздуха почти отсутствует. Значит, на таких высотах силу притяжения Земли компенсирует центробежная сила, которая появляется благодаря скорости спутника (рис. 2.4).
В этом случае:
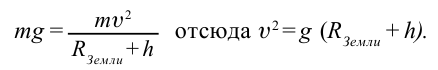
В случае, когда высоту 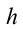 по сравнению с радиусом Земли
по сравнению с радиусом Земли 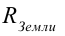 можно не учитывать,
можно не учитывать,

Чтобы вычислить значение 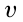 , принимаем
, принимаем 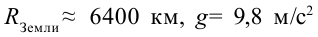 , соответственно
, соответственно 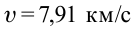 .
.
Эта скорость называется первой космической скоростью.
Искусственный спутник Земли, который двигается с такой скоростью, делает один оборот вокруг Земли за время: 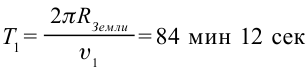 .
.
На практике время, за которое спутник совершает один оборот, больше чем расчетное время. Причина этого явления в том, что радиус орбиты спутника и радиус Земли отличаются друг от друга.
Таким образом, скорости спутников, вращающихся на орбитах с большими радиусами, будут меньше, чем скорости спутников, вращающихся на орбитах, близких к поверхности Земли.
Период вращения таких спутников вычисляется по формуле:
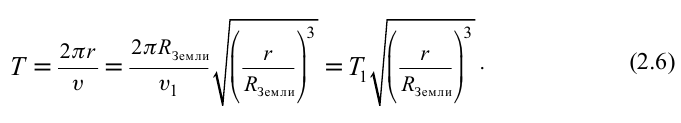
Здесь: 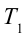 – период вращения спутников, вращающихся на орбитах, близких к поверхности Земли.
– период вращения спутников, вращающихся на орбитах, близких к поверхности Земли.
Используя формулу периода вращения спутника, вращающегося на произвольных высотах, можно вычислить необходимое расстояние от Земли, на котором спутник должен зафиксироваться. На какой высоте должен двигаться спутник, чтобы период его вращения был равен 24 часам? Расчеты показали, что высота составляет:
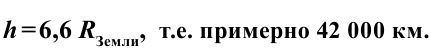
Такая орбита называется геостационарной орбитой.
Впервые на нашей планете 4 октября 1957 года на территории бывшего СССР был запущен первый искусственный спутник Земли. Спутник имел форму шара диаметром 58 см и массой 83,6 кг. Этот спутник совершил вокруг Земли 1400 оборотов, т.е. преодолел расстояние в 60 миллионов километров. А 12 апреля 1961 года первый человек полетел в космос. Первый космонавт Юрий Алексеевич Гагарин был гражданином бывшего СССР. 20 июля 1969 года американские астронавты Нейл Армстронг и Эдвин Олдрин впервые совершили посадку на Луну.
Для того чтобы долететь до планет Солнечной системы, космический корабль должен преодолеть вторую космическую скорость, равную 11,2 км/с.
Для достижения далеких звезд потребуется преодолеть силу притяжения Солнечной системы, т.е. космический корабль должен двигаться с третьей космической скоростью. Величина третьей космической скорости равна 16,7 км/с.
Среди космонавтов, которые многократно летали в космос, наш соотечественник В. Джанибеков и представитель узбекской нации С. Шарипов.
Гравитационное поле и сила притяжения
Шесть из восьми планет Солнечной системы были открыты благодаря наблюдениям за звездным небом. Именно так в 1781 г. английский астроном Джон Гершель открыл Уран. Впрочем, планета вела себя «странно»: ее орбита не соответствовала расчетам, основанным на законе всемирного тяготения. Ученые предположили, что рядом с Ураном есть еще одна планета, и начали искать ее с помощью... математики.
Рассчитать орбиту новой планеты удалось англичанину Джону Адамсу и французу Урбену Леверье. 23 августа 1846 г. немецкий астроном Иоганн Галле навел телескоп на указанное Леверье место и... увидел планету! Нептун — восьмая планета Солнечной системы — стал первым космическим объектом, открытым «на кончике пера».


Как определить силу гравитационного притяжения
Гравитационное взаимодействие — взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу. Гравитационное взаимодействие происходит посредством гравитационного поля, которое существует вокруг любого тела: звезды, планеты, человека, молекулы и т. д. Выведем закон всемирного тяготения, следуя логике рассуждений Ньютона, который и установил данный закон.
- Благодаря гравитационному взаимодействию Земля придает всем телам вблизи ее поверхности ускорение g=F/m (второй закон Ньютона). Данное ускорение не зависит от массы тела — это возможно, если сила гравитационного взаимодействия прямо пропорциональна массе тела (
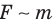 ).
). - Два тела массами
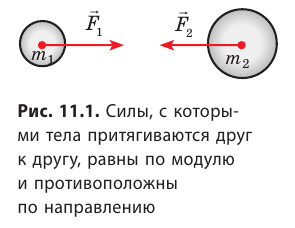
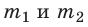 взаимодействуют с равными по модулю силами (третий закон Ньютона):
взаимодействуют с равными по модулю силами (третий закон Ньютона): 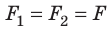 (рис. 11.1). При этом
(рис. 11.1). При этом 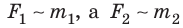 . Следовательно, сила гравитационного взаимодействия двух тел прямо пропорциональна произведению масс этих тел:
. Следовательно, сила гравитационного взаимодействия двух тел прямо пропорциональна произведению масс этих тел:
- Проанализировав движение Луны вокруг Земли и опираясь на законы Кеплера (законы вращения планет вокруг Солнца), Ньютон доказал, что сила гравитационного притяжения двух тел обратно пропорциональна квадрату расстояния между ними:
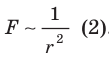 .
.
Объединив выводы (1) и (2), И. Ньютон получил закон всемирного тяготения: Любые два тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними: F G m m r = 1 2 2 , (3) где G — гравитационная постоянная (коэффициент пропорциональности, одинаковый для всех тел во Вселенной).
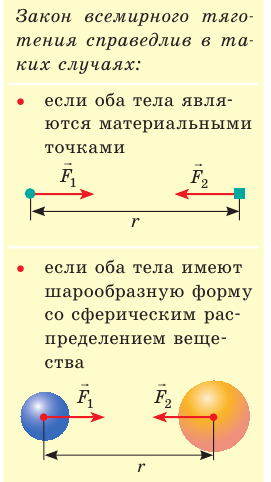
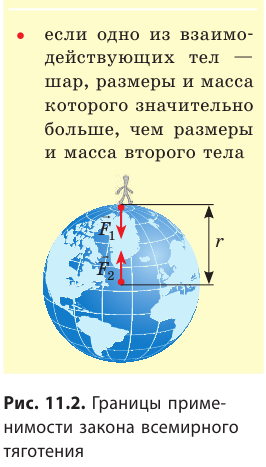
Закон всемирного тяготения имеет определенные границы применимости (рис. 11.2). Только в XX в. было установлено: когда гравитационные поля настолько сильны, что разгоняют тела до скоростей порядка скорости света, или когда частицы, пролетающие вблизи массивных тел, еще на отдалении имеют скорость, сравнимую со скоростью света, силу гравитационного притяжения нельзя рассчитать по закону всемирного тяготения. В общем случае тяготение описывается общей теорией относительности.
Как измерить гравитационную постоянную
Гравитационная постоянная G — одна из фундаментальных констант в физике. По современным данным, значение гравитационной постоянной составляет:
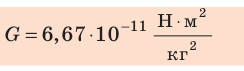
Из формулы (3) следует: 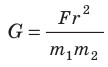 . То есть, если r= 1 м, а
. То есть, если r= 1 м, а 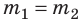 =1 кг, то G численно равна F. Гравитационная постоянная численно равна силе гравитационного притяжения двух материальных точек массой 1 кг каждая, находящихся на расстоянии 1 м друг от друга.
=1 кг, то G численно равна F. Гравитационная постоянная численно равна силе гравитационного притяжения двух материальных точек массой 1 кг каждая, находящихся на расстоянии 1 м друг от друга.
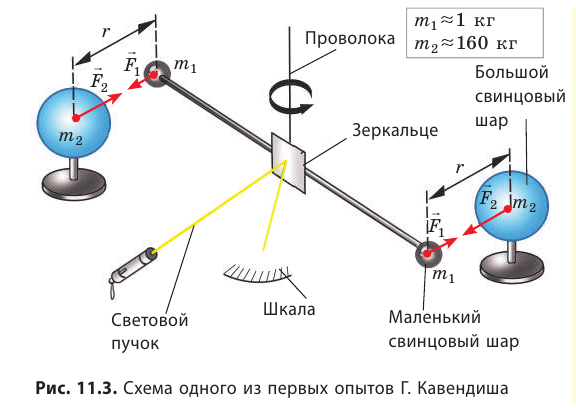
- В результате притяжения шаров проволока закручивается. Угол закручивания проволоки регистрируют на шкале по повороту светового пучка, отражающегося от зеркальца.
- По углу закручивания проволоки определяют силу F гравитационного притяжения.
- Измеряют расстояние r между центрами шаров.
- Зная массы
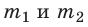 шаров, вычисляют гравитационную постоянную:
шаров, вычисляют гравитационную постоянную: 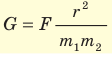
Измерить гравитационную постоянную достаточно сложно: гравитационное притяжение между телами становится заметным только при очень большой массе хотя бы одного из тел.
Гравитационную постоянную впервые измерил английский ученый Генри Кавендиш (1731–1810) в 1798 г. с помощью крутильных весов (рис. 11.3).
Как «взвесить» Землю
Опыт Г. Кавендиша еще называют «взвешиванием Земли». Как можно измерить массу Земли и любой другой планеты? Вспомним о силе тяжести.
Сила тяжести 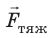 — это сила, с которой Земля (или другое астрономическое тело) притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.
— это сила, с которой Земля (или другое астрономическое тело) притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.
Сила тяжести направлена вертикально вниз и приложена к точке, которую называют центром тяжести тела.
- Согласно закону всемирного тяготения модуль силы тяжести, действующей на тело массой m со стороны Земли, равен:
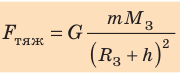 (1). Здесь
(1). Здесь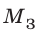 — масса Земли;
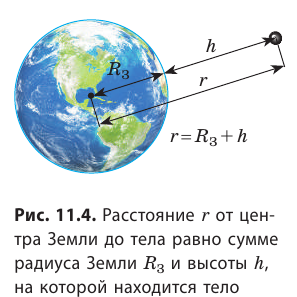
— масса Земли; 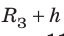 — расстояние от центра Земли до тела (рис. 11.4).
— расстояние от центра Земли до тела (рис. 11.4). - Согласно второму закону Ньютона:
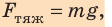 (2), где g — ускорение свободного падения на высоте h.
(2), где g — ускорение свободного падения на высоте h.
Приравняв правые части формул (1) и (2), получим формулу для вычисления ускорения свободного падения:
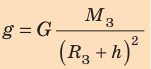
Проанализировав последнюю формулу, приходим к следующим выводам.
- Ускорение свободного падения не зависит от массы тела (доказано Г. Галилеем).
- Ускорение свободного падения уменьшается при подъеме тела над поверхностью Земли (заметное изменение происходит при подъеме на десятки и сотни километров).
- Если тело находится на поверхности Земли (h= 0) или вблизи нее
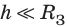 , ускорение свободного падения вычисляют по формуле:
, ускорение свободного падения вычисляют по формуле: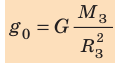
- Вблизи поверхности Земли ускорение свободного падения известно (
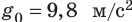 ), следовательно, можем определить массу Земли:
), следовательно, можем определить массу Земли: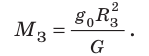
Отметим, что из-за вращения Земли, а также из-за того, что форма Земли — геоид, ускорение свободного падения зависит от географической широты местности (рис. 11.5).
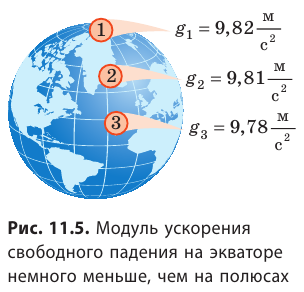
Ускорение свободного падения в определенной местности может отличаться от его средних значений на данной широте. Причины — в неоднородности земной коры, наличии гор и впадин; в различной плотности пород, залегающих в недрах Земли. Так, уменьшение ускорения свободного падения часто свидетельствует о залежах торфа, нефти, газа; увеличение — о залежах металлических руд. Метод поиска залежей полезных ископаемых по точному определению ускорения свободного падения называют гравиметрической разведкой.
Первая космическая скорость
Представим, что мы стреляем из пушки в горизонтальном направлении, с каждым выстрелом увеличивая скорость движения ядра. Траектория движения ядер будет параболической, и каждый раз ядра будут падать все дальше. Если представить, что Земля плоская, на этом наш эксперимент можно было бы и завершить, но Земля имеет форму шара, поэтому с каждым выстрелом она все больше и больше будет «уходить» из-под ядра (рис. 11.6). Теперь представим, что сопротивление воздуха отсутствует, а мы придали ядру такую большую скорость, что оно облетело вокруг Земли и вернулось к месту выстрела.
При этом ядро не остановится, а будет и дальше двигаться с неизменной скоростью, «наматывая круги» вокруг планеты. Другими словами, мы получим искусственный спутник Земли.
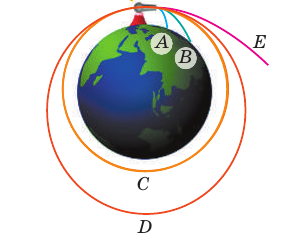
Рис. 11.6. Движение тела под действием силы тяжести (по рисунку И. Ньютона): ядра A и B падают на Землю, ядро C выходит на круговую орбиту, D — на эллиптическую, ядро E летит в открытый космос
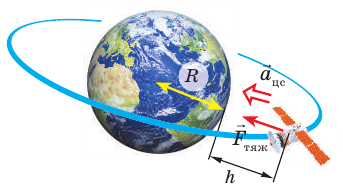
Рис. 11.7. На спутник, движущийся по круговой орбите на высоте h над поверхностью планеты, действует одна сила — сила тяжести 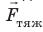 , которая и придает спутнику центростремительное ускорение
, которая и придает спутнику центростремительное ускорение 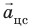
Скорость, которую надо сообщить объекту, чтобы он двигался вокруг планеты по круговой орбите, называют первой космической скоростью.
Первую космическую скорость v можно вычислить, учитывая, что именно сила тяжести придает телу центростремительное ускорение (рис. 11.7). По второму закону Ньютона:
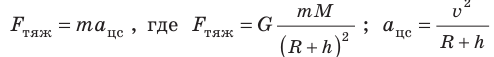
Следовательно, 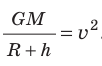 . Отсюда получаем формулу для вычисления первой космической скорости движения спутника на высоте h над поверхностью планеты:
. Отсюда получаем формулу для вычисления первой космической скорости движения спутника на высоте h над поверхностью планеты: 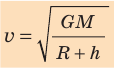 .
.
Для случаев вблизи поверхности Земли (h≈ 0) данная формула принимает вид: 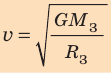 . Вспомним, что у поверхности Земли
. Вспомним, что у поверхности Земли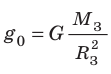 , то есть
, то есть 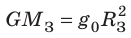 . После упрощения получим:
. После упрощения получим: 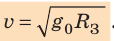 .
.
Поскольку 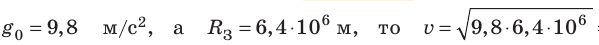 =
=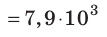 (м/с) — первая космическая скорость у поверхности Земли.
(м/с) — первая космическая скорость у поверхности Земли.
4 октября 1957 г. Советский Союз вывел на орбиту первый искусственный спутник Земли — ПС-1. Его разработали С. П. Королев, М. В. Келдыш, М. К. Тихонравов и другие выдающиеся ученые. ПС-1 представлял собой небольшую сферу диамет ром 58 см и массой 83,6 кг, оснащенную четырьмя антеннами длиной 2,4 и 2,9 м для передачи сигнала.

Спутник отделился от второй ступени ракеты-носителя на 315-й секунде после старта и почти сразу начал передавать сигнал, который слышали не только специалисты, но и радиолюбители практически всех стран. С этого момента начался отсчет космической эры человечества.
«Тот маленький огонек, стремительно двигающийся от края и до края неба... сделал человечество бессмертным», — писал американский писатель-фантаст Рэй Брэдбери. В течение 92 суток полета спутник совершил 1440 оборотов вокруг Земли, после чего сгорел в атмосфере. Траекторию движения спутника на карту звездного неба первыми нанесли наблюдатели Лаборатории космических исследований Ужгородского государственного университета.
Выводы:
- Взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным, а само явление взаимного притяжения тел — всемирным тяготением или гравитацией.
- Закон всемирного тяготения: любые два тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:
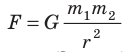
- Силу, характеризующую гравитационное взаимодействие тел с Землей (или с другим астрономическим телом), называют силой тяжести. Сила тяжести направлена вертикально вниз и приложена к центру тяжести тела. Модуль силы тяжести можно вычислить по формулам:
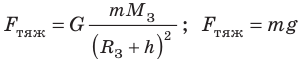
- Скорость v, которую надо придать объекту, чтобы он двигался вокруг планеты по круговой орбите, называют первой космической скоростью:
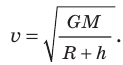
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея