
Движение твердого тела в теоретической механике
Движение твердого тела:
В общем случае движения твердого тела положение его в пространстве определяется тремя точками А, В и С, связанными с телом и расположенными не на одной прямой. Выбрав одну из точек, например А, за полюс (рис. 208), можно тело из данного положения ABC переместить в какое-либо другое 
- дав телу поступательное перемещение вместе с полюсом А в положение
- повернув тело вокруг оси L, проходящей через полюс А до совпадения с требуемым положением
 , что по теореме Эйлера возможно.
, что по теореме Эйлера возможно.
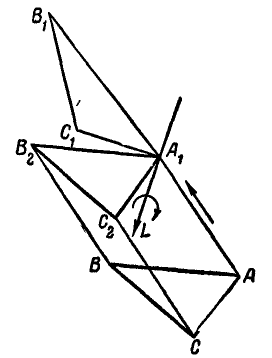
Рис. 208.
Так же как и в случае плоского движения, здесь поступательная часть движения, твердого тела зависит от выбора полюса, вращательная же часть не зависит. Итак, любое перемещение тела можно разложить на поступательное, определяемое выбором полюса, и вращательное вокруг некоторой оси, проходящей через выбранный полюс.
Посмотрим теперь, как может быть задано движение тела.
Пусть тело А (рис. 209) движется как угодно в пространстве. Проведем через точку М тела координатные оси 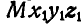 , которые во все время движения тела будут оставаться параллельными неподвижным осям Oxyz.
, которые во все время движения тела будут оставаться параллельными неподвижным осям Oxyz.
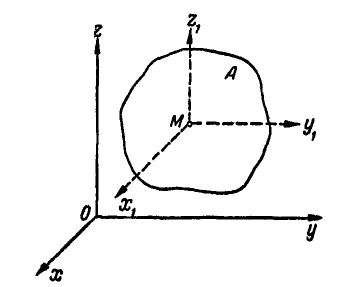
Рис. 209.
Если бы твердое тело было жестко связано с системой 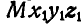 , то оно двигалось бы поступательно, но так как тело имеет возможность вращаться около выбранной точки М, то его движение состоит из поступательного вместе с точкой М и вращательного вокруг точки М. Ясно, что положение тела в любой момент будет вполне определено, если будут заданы координаты х, у и z движущейся точки М и эйлеровы углы
, то оно двигалось бы поступательно, но так как тело имеет возможность вращаться около выбранной точки М, то его движение состоит из поступательного вместе с точкой М и вращательного вокруг точки М. Ясно, что положение тела в любой момент будет вполне определено, если будут заданы координаты х, у и z движущейся точки М и эйлеровы углы 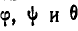 , как функции времени, т.е.:
, как функции времени, т.е.:
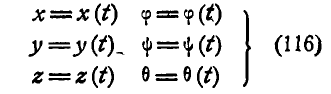
Эти уравнения называются уравнениями движения тела в общем случае его движения. Первые три из уравнений (116) определяют уравнение движения точки М, а последние три — поворот тела вокруг М, который, как известно, в данный момент можно осуществить вокруг мгновенной оси, проходящей через точку М.
В отличие от вращения тела вокруг неподвижной точки, в общем случае движения тела точка М его движется с некоторой скоростью. Поэтому для нахождения скорости любой точки тела, движущегося как угодно, следует к скорости точки, определяемой формулами Эйлера (112), прибавить еще скорость и точки М. Обозначая проекции скорости любой точки тела на неподвижные оси 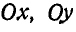 и
и 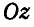 через
через 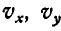 и
и 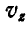 , имеем:
, имеем:
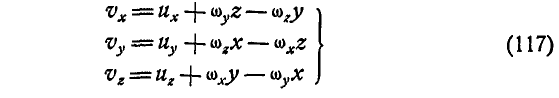
В частности, если тело движется в плоскости хОу, то вращение его может происходить только вокруг оси, перпендикулярной к этой плоскости, а поэтому, полагая в формулах (117) 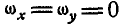 , и
, и 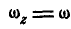 , и
, и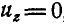 , получим:
, получим:
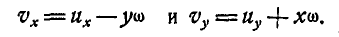
Дифференцируя равенства (117) по времени 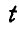 , можно получить проекции ускорения любой точки тела на неподвижные оси Ох, Оу и Oz.
, можно получить проекции ускорения любой точки тела на неподвижные оси Ох, Оу и Oz.
Покажем теперь, что любое мгновенное перемещение тела из одного положения в другое может быть получено одним винтовым движением.
В самом деле, нами было показано (рис. 208), что перемещение свободного тела из положения ABC в положение  можно осуществить одним поступательным движением в направлении
можно осуществить одним поступательным движением в направлении  и одним вращательным вокруг оси L, Рассмотрим движение тела за бес конечно малый промежуток времени Обозначим вектор мгновенной скорости поступательного движения через
и одним вращательным вокруг оси L, Рассмотрим движение тела за бес конечно малый промежуток времени Обозначим вектор мгновенной скорости поступательного движения через 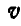 , а вектор мгновенной угловой скорости вращательного движения вокруг оси L и направленный вдоль этой оси, — через
, а вектор мгновенной угловой скорости вращательного движения вокруг оси L и направленный вдоль этой оси, — через 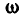 (рис. 210).
(рис. 210).
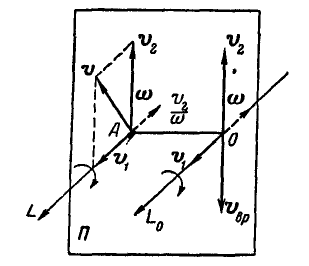
Рис. 210.
Проведем через точку А плоскость П, перпендикулярную к оси L, и разложим вектор 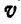 на два составляющих вектора
на два составляющих вектора 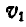 и
и 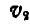 , из которых вектор
, из которых вектор 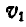 направлен вдоль оси L, а вектор
направлен вдоль оси L, а вектор 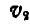 , расположенный в пересечении плоскостей П и плоскости (v, L), к нему перпендикулярно.
, расположенный в пересечении плоскостей П и плоскости (v, L), к нему перпендикулярно.
Восстановим в точке А перпендикуляр, расположенный в плоскости П, к вектору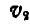 и отложим на этом перпендикуляре от точки А отрезок AO
и отложим на этом перпендикуляре от точки А отрезок AO 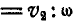 . Тогда скорость точки О вследствие поступательного движения тела со скоростью
. Тогда скорость точки О вследствие поступательного движения тела со скоростью 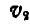 и вращательного вокруг оси L с угловой скоростью
и вращательного вокруг оси L с угловой скоростью 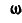 , будет равна:
, будет равна: 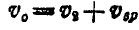 .
.
Легко видеть, что векторы скоростей 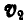 и
и 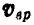 направлены по одной прямой в противоположные стороны, причем
направлены по одной прямой в противоположные стороны, причем 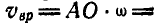
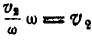 , а поэтому скорость
, а поэтому скорость 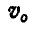 точки О от указанных двух движений тела равна нулю. Таких точек О, расположенных на оси
точки О от указанных двух движений тела равна нулю. Таких точек О, расположенных на оси 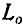 параллельной оси L, будет бесчисленное множество и все они будут обладать линейной скоростью
параллельной оси L, будет бесчисленное множество и все они будут обладать линейной скоростью 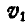 направленной вдоль оси
направленной вдоль оси 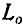 .
.
Следовательно, мы показали, что в каждый момент времени перемещение свободного тела приводится к вращению вокруг некоторой оси 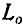 с угловой скоростью
с угловой скоростью 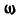 и к поступательному перемещению вдоль этой оси, т. е. к мгновенному винтовому движению.
и к поступательному перемещению вдоль этой оси, т. е. к мгновенному винтовому движению.
Центральная ось 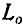 этого движения называется мгновенной винтовой осью.
этого движения называется мгновенной винтовой осью.
Проекции ускорения любой точки тела на неподвижные оси Ох, Оу и Oz, как было упомянуто выше, можно получить путем дифференцирования равенств (117) по времени t.
Всё о движении твердого тела
Движение твердого тела в пространстве определяется движением трех его точек, не лежащих на одной прямой
Движение твердого тела. Далеко не во всех задачах кинематики можно пренебрегать размерами движущегося тела и принимать его за точку. Для тех случаев, когда расстояния между частицами тела не изменяются, но по условиям задачи приходится учитывать движения его различных частиц, разработан раздел кинематики, называемый кинематикой твердого тела.
Мы неизменно связываем движущееся твердое тело с осями координат x'Ey'z', которые движутся вместе с ним. Тогда движение тела него точек определяется движением системы координат x'Ey'z',. В кинематике часто допускают, что это тело имеет неограниченные размеры.
Если закрепить две точки твердого тела, то оно сможет поворачиваться вокруг прямой, проходящей через эти две точки. Если закрепить еще и третью точку, не лежащую на той же прямой, то все тело окажется закрепленным. Таким образом, положение твердого тела определяется положением трех его точек, не лежащих на одной прямой, а движение тела—движением трех его точек.
Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой
Основная теорема кинематики твердого тела. Рассмотрим какие-либо две точки А и В твердого тела и их скорости. Проведем прямую через точки А и В и спроецируем на нее скорости точек А и В
(рис. 96). Существует теорема о том, что проекции скоростей двух точек тела на прямую, соединяющую эти точки, всегда равны между собой. Из множества имеющихся доказательств этой теоремы приведем следующее логическое доказательство: проекции скоростей двух точек абсолютно твердого тела на прямую, соединяющую эти точки, равны между собой, так как в противном случае расстояние AB между этими точками изменялось бы:
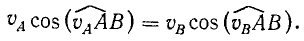 (77)
(77)
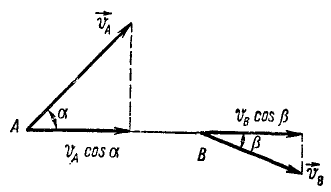
Рис. 96
Эта теорема относится, разумеется, не только к двум точкам А и В, а ко всем точкам, составляющим прямую, и может быть сформулирована так: проекции на какую-либо ось, проведенную в твердом теле, скоростей точек этой оси равны между собой.
Задача:
Плоская фигура движется в своей плоскости, при этом точка А фигуры движется по оси Оу, а точка В фигуры —по оси Ox системы координат. При каком соотношении координат точек А и В υA = 2υB?
Решение:
Проекции скоростей точек Л и В на прямую AB равны между собой. Косинус угла между направлением скорости и прямой AB равен υА и и между скоростью υB и той же прямой и, следовательно,
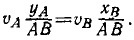
Подставляя вместо од его требуемое значение 2υB, получаем ответ.
Ответ: хB = 2υB∙
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Сложение движений точки
- Сложение движений твердого тела в теоретической механике - формулы и определения с примерами
- Динамика материальной точки
- Движение материальной точки
- Вращение твердого тела вокруг неподвижной оси
- Сферическое движение твердого тела
- Плоско-параллельное движение твердого тела
- Движение твердого тела, имеющего неподвижную точку