
Движение тел под воздействием нескольких сил в физике - формулы и определение с примерами
Движение тел под воздействием нескольких сил:
Во время изучения второго закона Ньютона рассматривался случай, когда на тело действовала одна сила. Третий закон Ньютона описывает процесс взаимодействия тел при участии нескольких сил. В повседневной жизни тоже не наблюдаются случаи, где на тело действует только одна сила. На двигающиеся тела, кроме силы притяжения, также действует и сила трения. На тело с массой 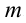
Здесь воспользуемся понятием равнодействующая сила. Равнодействующей силой принято считать геометрическую сумму всех приложенных к телу сил, т.е. результирующую силу. В данном случае получаем:
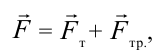
Берется алгебраическая сумма силы притяжения и силы трения. В этом случае силы, действующие на тело, направлены противоположно, и ее модуль определяется как:
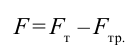
Полученное телом ускорение по второму закону Ньютона определяется из выражения:

Рассмотрим две задачи, в которых на тело действует несколько сил.
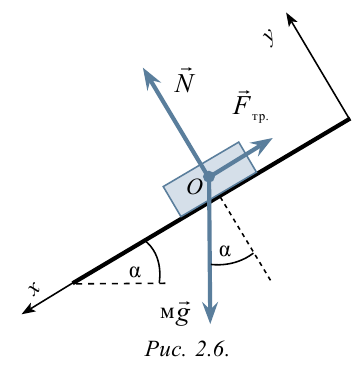
1. Рассмотрим условия равновесия и ускорение падения тела, установленного на наклонной плоскости (рисунок 2.6). Здесь 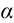 – угол наклона плоскости. Коэффициент трения наклонной плоскости и доски, поставленной на ней, равен
– угол наклона плоскости. Коэффициент трения наклонной плоскости и доски, поставленной на ней, равен 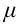 .
.
На доску, находящуюся на наклонной плоскости, действуют: сила тяжести 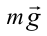 , нормальная сила реакции
, нормальная сила реакции 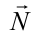 и направленная вверх по наклонной плоскости сила трения в состоянии покоя
и направленная вверх по наклонной плоскости сила трения в состоянии покоя 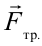 .
.
Ось 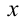 направляем вниз по плоскости, ось
направляем вниз по плоскости, ось 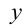 направляем перпендикулярно к плоскости.
направляем перпендикулярно к плоскости.
Чтобы тело оставалось в равновесии на наклонной плоскости, равнодействующая сила действующих на него сил должна быть равна нулю:
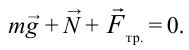
Исходя из этого составим системы уравнений для проекции на оси
координат:
- По оси
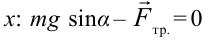 ;
; - По оси y: mg cosα + N = 0.
Чтобы тело оставалось в равновесии на наклонной плоскости, должно выполняться неравенство: 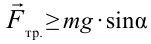 .
.
Согласно первого уравнения 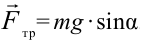 , по второму уравнению
, по второму уравнению 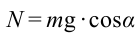 . Если учесть эти выражения и уравнение
. Если учесть эти выражения и уравнение 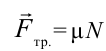 , выполнится неравенство:
, выполнится неравенство: 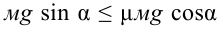 . Из этого получаем:
. Из этого получаем: 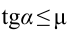 .
.
Таким образом, при выполнении условия 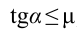 , доска остается в равновесии на наклонной плоскости.
, доска остается в равновесии на наклонной плоскости.
При условии 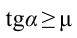 тело движется с ускорением вниз по наклонной плоскости. Чтобы найти ускорение составим уравнение:
тело движется с ускорением вниз по наклонной плоскости. Чтобы найти ускорение составим уравнение: 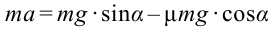 . Разделив обе стороны уравнения на
. Разделив обе стороны уравнения на  , получаем:
, получаем:

2. На неподвижный блок, с ничтожной малой массой подвешены грузы с массами  и
и 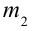 (рисунок 2.7). Если
(рисунок 2.7). Если 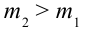 , найти ускорение движения грузов и натяжения нити. Силой трения на блоке и массой нити пренебречь.
, найти ускорение движения грузов и натяжения нити. Силой трения на блоке и массой нити пренебречь.
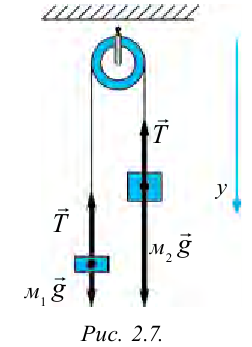
На каждый груз действуют две силы: сила тяжести и сила натяжения нити. Требование не учитывать массу блока и нити, а также силу трения означает, что они одинаковы на обоих сторонах нити. Силу натяжения нити обозначим 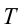 .
.
В связи с тем, что нить не растяжима, модуль перемещения грузов и соответственно скорость и ускорение будут равными. Модуль ускорения грузов обозначим как 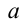 . Тогда, направив ось
. Тогда, направив ось 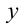
вниз, для проекции на ней составим систему уравнений:
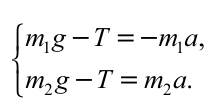
Из второго уравнения вычитаем первое уравнение:
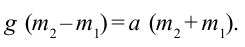
Отсюда

Решаем оба уравнения относительно Т и получаем 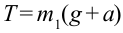 в первом уравнении и
в первом уравнении и 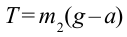 во втором уравнении. Это – вес тел, одно из которых движется с ускорением вниз, а второе вверх. Из-за того, что тела движутся с ускорением, их вес будет одинаковым, несмотря на разные массы. Если подставить выражение, найденное для ускорения, в формулу для расчета силы натяжении нити с любой стороны блока, то получим:
во втором уравнении. Это – вес тел, одно из которых движется с ускорением вниз, а второе вверх. Из-за того, что тела движутся с ускорением, их вес будет одинаковым, несмотря на разные массы. Если подставить выражение, найденное для ускорения, в формулу для расчета силы натяжении нити с любой стороны блока, то получим:

Из этой формулы находим вес каждого груза.

Основные понятия, правила и законы:
| Формулировка пер- вого закона динамики по Галилею. |
Если на тело не действуют другие тела, то оно сохраняет свое состояние покоя или прямолинейного равномерного движения относительно Земли. |
| Первый закон динамики |
Существуют такие системы отсчета, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действует сила, или действие внешних сил взаимно скомпенсировано. |
| Сила | Количественное измерение причины получения ускорения тел в результате взаимодействия друг с другом. |
| Инертная масса | Физическая величина, определяемая соотношением 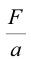 |
| Второй закон динамики |
Полученное телом ускорение прямо пропорционально приложенной к нему силе и обратно пропорционально массе тела: 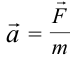 ; произведение ; произведениемассы тела на ускорение равно действующей на тело силе: 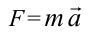 (под «силой» понимается (под «силой» понимаетсяравнодействующая всех сил). |
| Третий закон динамики |
Действие равно противодействию. Тела действуют друг на друга с силами, направленными противоположно вдоль одной и той же прямой, и равными по значению: 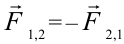 . . |
| Инерциальные системы отсчета |
Системы отсчета, относительно которых материальная точка находится в покое или двигается прямолинейно и равномерно. |
| Неинерциальные системы отсчета |
Системы отсчета, которые двигаются криволинейно или с ускорением. |
| Сила инерции | Сила, которая появляется в результате движения с ускорением |
| Первая космическая скорость |
Скорость, которая необходима телу, чтобы стать искусственным спутником Земли – 7,91 км/с. |
| Вторая космическая скорость |
Скорость, необходимая для полета к планетам солнечной системы – 11,2 км/с. |
| Третья космическая скорость |
Скорость, необходимая для преодоления силы притяжения Солнечной системы и выхода за ее пределы – 16,7 км/с. |
| Вес тела при движении вертикально с ускорением 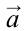 |
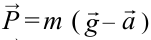 – вес тела, опускающегося вниз. – вес тела, опускающегося вниз.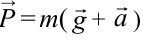 – вес тела, поднимающегося вверх. – вес тела, поднимающегося вверх. |
| Невесомость | Состояние, при котором сила взаимодействия тела с опорой или подвесом равна нулю. |
| Перегрузка | 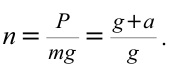 |
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |