Движение несвободной материальной точки в теоретической механике

Движение несвободной материальной точки:

Как уже известно, основной закон динамики для несвободной материальной точки, а следовательно, и ее дифференциальные уравнения движения имеют такой же вид, как и для свободной точки, только к действующим на точку силам добавляют все силы реакций связей. Естественно, что в этом случае движения точки могут возникнуть соответствующие особенности при решениях первой и второй основных задач динамики, так как силы реакций связей заранее не известны и их необходимо дополнительно определить по заданным связям, наложенным на движущуюся материальную точку.

При решении первой основной задачи динамики действующая на точку равнодействующая сила определяется по заданному движению точки из дифференциальных уравнений ее движения. Затем из этой равнодействующей силы по заданным связям выделяют силу реакции связей. Таким образом получается задача о разложении известной силы на ее составляющие.

Полную силу реакции точки при ее движении обычно разлагают на две составляющие. Составляющая силы реакции связей, уравновешивающая заданные силы, приложенные к точке, называется статической реакцией. Другая составляющая полной силы реакции, зависящая только от движения точки под действием заданных сил, называется динамической реакцией. Она уравновешивает силу инерции движущейся точки.

При решении второй основной задачи динамики, когда по заданным силам и начальным условиям требуется определить движение несвободной точки, часть сил, действующих на точку, а именно все силы реакций связей, заранее не известны и их необходимо определить по заданным связям в процессе решения задачи. Таким образом, вторую основную задачу динамики для несвободной материальной точки можно сформулировать так: по заданным силам, начальным условиям и связям, наложенным на точку, определить движение этой точки и силы реакции связей.

Рассмотрим решение этой задачи для движения точки по поверхности и кривой линии. Дифференциальные уравнения при этом выражают в той системе координат, которая наиболее соответствует конкретной задаче. Разберем постановку и решение задачи в прямоугольной декартовой системе координат.

Движение точки по поверхности

Пусть гладкая неподвижная поверхность, по которой движется точка массой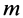 

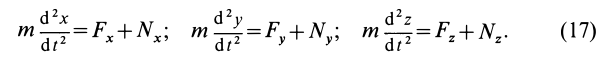
Из дифференциальной геометрии известно, что косинусы углов внешней нормали к поверхности с осями координат, а следовательно, и силы 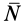, параллельной главной нормали, можно вычислить по формулам

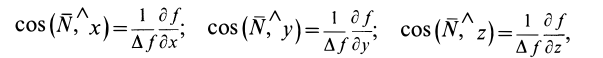
где

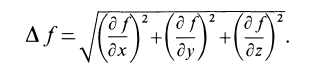
Таким образом,

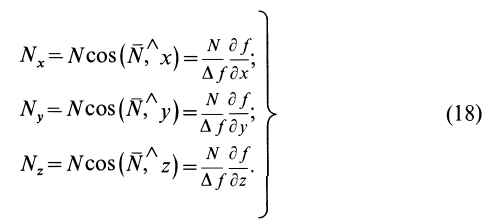
Обозначив 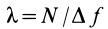 и подставив значения 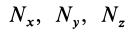из (18) в (17), получим:

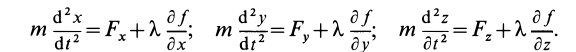
Эти дифференциальные уравнения называют дифференциальными уравнениями Лагранжа первого рода для движения несвободной материальной точки. Из этих трех дифференциальных уравнений и одного конечного уравнения — уравнения поверхности 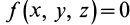— можно найти четыре неизвестных—координаты точки 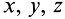и неопределенный множитель Лагранжа 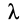как функции времени и произвольных постоянных интегрирования. Произвольные постоянные определяют из начальных условий.

По найденному неопределенному множителю Лагранжа 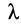, легко определить силу реакции поверхности 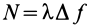, которая в общем случае зависит от времени.

'Если поверхность не гладкая, то кроме нормальной силы реакции возникает предельная сила трения 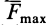, проекции которой надо добавить в правые части дифференциальных уравнений движения точки. Это добавление усложнит решение задачи, но задача и в этом случае принципиально разрешима, так как наряду с добавлением неизвестной силы добавляется и конечное уравнение, связывающее эту силу с нормальной реакцией:

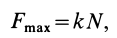
где 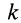 — коэффициент трения.

Так как сила трения скольжения всегда направлена против скорости, то проекции этой силы на оси координат можно представить в виде

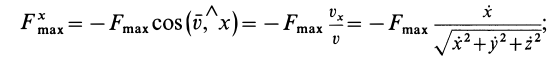
аналогично,

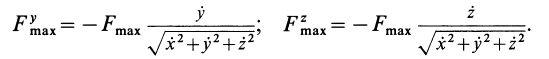
Учет силы трения значительно усложняет задачу интегрирования дифференциальных уравнений движения несвободной материальной точки.

Движение точки по гладкой кривой линии

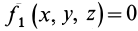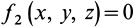Кривую неподвижную линию в пространстве можно рассматривать как линию пересечения двух поверхностей: и . Эти поверхности создадут для движущейся точки две нормальные реакци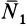и  и 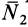, и поэтому полная реакция кривой линии .

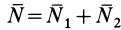Дифференциальные уравнения Лагранжа первого рода движения точки по кривой линии имеют вид

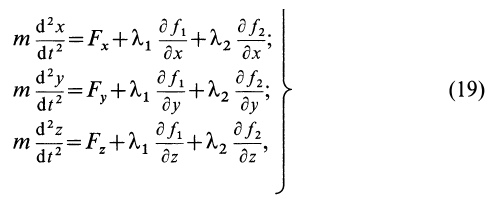
где соответственно

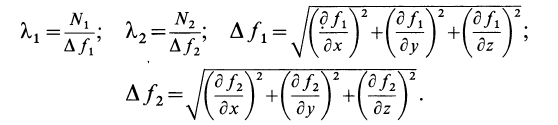
Присоединяя к дифференциальным уравнениям Лагранжа первого рода (19) два конечных уравнения поверхносте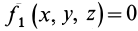й и 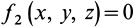, получаем пять уравнений для определения пяти величин 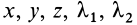как функций времени. Таким образом, и в этом случае поставленная задача может быть разрешена. Она принципиально разрешима и при учете силы трения.

Если при рассмотрении этой задачи за оси координат взять естественные оси, то дифференциальные уравнения движения точки по гладкой кривой примут вид

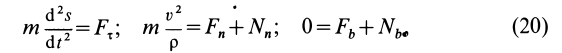
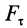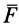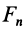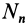где — проекция силы на касательную;  и  — проекции сил на главную нормаль; 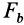и 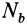— проекции сил на бинормаль; 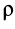— радиус кривизны кривой линии.

Из первого дифференциального уравнения системы (20) независимо от двух других уравнений можно найти закон движения точки и, следовательно, скорость точки 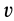. После этого из двух оставшихся уравнений (20) можно определить проекции неизвестной нормальной реакции 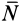соответственно на главную нормаль и бинормаль.

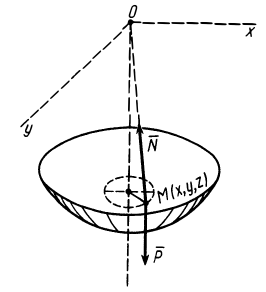
Рис. 13

• Заказать решение задач по теоретической механике

Пример:

Материальная точка массой 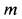(рис. 13) движется под действием силы тяжести по внутренней части поверхности сферы радиуса  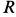 вблизи устойчивого положения равновесия. В начальный момент 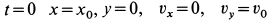. Ось 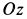 направлена по вертикали вниз, а 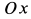и 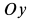 расположены в горизонтальной плоскости. Начало координат находится в центре сферы.

Определить движение точки и силу реакции абсолютно гладкой сферы на точку. Эта задача известна как задача о сферическом маятнике.

Решение:

Дифференциальные уравнения движения точки по поверхности сферы имеют вид

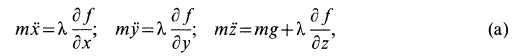
где

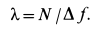
К дифференциальным уравнениям (а) следует добавить уравнение связи, т. е. уравнение поверхности сферы

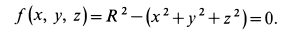
Тогда

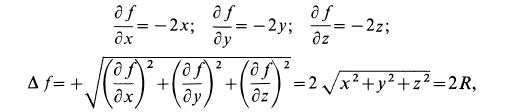
так как 

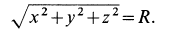
Подставляя в уравнения (а) значения производных 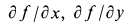и 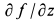, имеем:

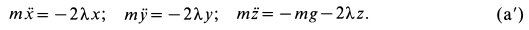
Эту систему и надо проинтегрировать. Для этого обычно из этих уравнений прежде всего исключают неизвестную 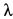, учитывая, что производные от нее не входят в уравнения (а'). Система уравнений сложна для интегрирования. Проинтегрируем ее приближенно. Для получения первого приближения сохраним в уравнениях только первые степени величин 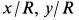и пренебрежем их квадратами в выражении для :

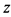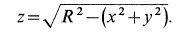
Разлагая это выражение по формуле для бинома, получаем

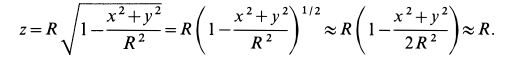
Полагая в третьем уравнении системы 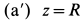 и 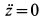, имеем

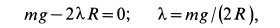
т. е.

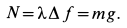
Подставляя значение 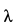в первые два уравнения системы (а'), получаем: 

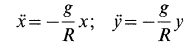или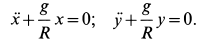

Решения этих дифференциальных уравнений (см. выше § 7, пример 1), зависящие каждое от двух постоянных интегрирования, имеют вид

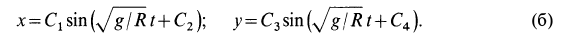
Дифференцируя их по времени, получаем

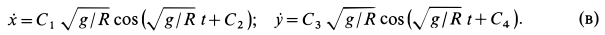
Используя начальные условия из (б) и (в), имеем следующие уравнения для определения постоянных интегрирования :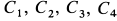

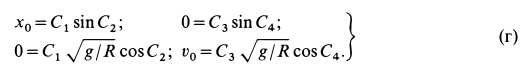
Из второго и третьего уравнений системы (г) находим 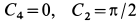. Подставляя эти значения в первое и четвертое уравнения, имеем

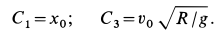
Искомые уравнения движения точки при принятом допущении принимают вид

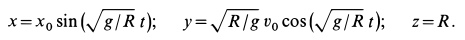
Если исключить из уравнений движения время 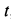, то получим уравнение траектории точки в координатной форме:

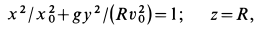
т. е. траекторией точки в принятом приближении является эллипс, расположенный в плоскости 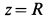с центром на оси .

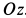Не следует думать, что система уравнений (а') проинтегрирована с точностью до членов первого порядка 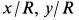, так как дополнительно принято 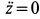. Если интегрирование уравнений выполнить с точностью до указанных слагаемых, приняв за первое приближение полученное решение, то вместо эллипса получится незамкнутая кривая, близкая на первом витке к эллипсу. Движение по такой незамкнутой кривой можно воспроизвести, если полученный эллипс поворачивать равномерно с определенной скоростью в сторону движения точки.