Движение материальной точки в теоретической механике

Динамика:

В динамике завершается изучение законов движения. Здесь объясняется, почему материальные точки или тела двигаются именно так, а не иначе, что служит причиной тех или иных изменений в характеристике их движения.

Первая аксиома динамики — закон инерции —объясняет, что равномерное и прямолинейное движение точки или тела происходит лишь в том случае, если на точку (тело) действует уравновешенная система сил. И наоборот, если нужно, чтобы точка или тело двигались равномерно и прямолинейно, то необходимо создать условия для равновесия всех сил, приложенных к данной точке или к данному телу.

В каждой задаче, в которой рассматривается криволинейное или неравномерное движение точки, применяется вторая аксиома динамики—основной закон динамики точки

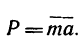
Закон равенства действия и противодействия (третья аксиома динамики) в задачах по динамике, так же как и в статике, используется при определении взаимодействия двигающихся тел.

Четвертая аксиома динамики— закон независимости действия сил — позволяет при решении задач динамики выбирать пути их решения. Если па материальную точку действует несколько сил, го можно найти их равнодействующую, а затем рассмотреть ее действие на точку — найти ускорение точки, но можно сначала найти ускорения, приобретенные от действия каждой силы отдельно, а затем эти ускорения геометрически сложить.

Решая любые задачи по динамике, необходимо учитывать, что все уравнения, выражающие основные законы динамики, а также многие формулы, как правило, выражены в форме, позволяющей использовать их лишь при подстановке числовых значений величин в единицах одной системы.

Поэтому перед тем как приступить к решению задачи по динамике, необходимо выбрать, в какой из двух употребляемых систем единиц решать задачу: либо в единицах СИ, либо в единицах МКГСС (единицах технической системы).

Заметим, что единицы длины (1 м), времени (1 сек), скорости (1 м/сек) и ускорения (1 м/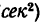

Как известно из статики, в СИ единицей силы служит 1 « — сила, сообщающая массе в 1 кг ускорение 1 м/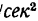, в системе МКГСС единицей силы служит 1 кГ — основная единица.

Единицей массы в СИ служит 1 кг (основная единица) —масса платино-иридиевого эталона, а в системе МКГСС—единица массы производная. Она образуется при подстановке в уравнение основного закона динамики

Р=m*а

вместо Р значения 1 кГ и вместо а значения 1 м/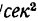, т. е. 

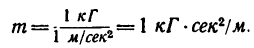
Таким образом, технической единицей массы (т. е. м.) является масса, которой сила, равная 1 кГ, сообщает ускорение 1 м/.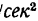

Техническая единица массы в 9,81 раза крупнее 1 кг (единицы СИ).

Основной закон динамики точки

Точка, движение которой ничем не ограничено, называется свободной. Свободная точка под действием приложенных сил может двигаться в каком угодно направлении. Задачи, в которых рассматривается свободная точка, решаются при помощи основного уравнения динамики

Если на точку действует только одна сила 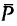(примером такого движения может служить так называемое свободное падение — движение точки под действием силы тяжести в безвоздушном пространстве), то векторное уравнение (а) заменяется скалярным уравнением

выражающим зависимость между модулями силы и ускорения.

Если на точку действует несколько сил 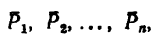то векторное уравнение (а) примет вид

где равнодействующая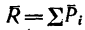 и, согласно закону независимости действия сил, 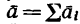(ускорение точки равно геометрической сумме ускорений, сообщенных ей каждой силой в отдельности).

Векторное равенство (в) заменяется двумя или тремя скалярными равенствами.

Если силы 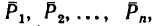действующие в одной плоскости, спроектировать на две взаимно перпендикулярные оси, получим два скалярных уравнения (уравнений проекций на оси х и у):

где 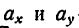— проекции ускорения 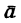соответственно на ось хну.

Если система сил, приложенных к точке,— пространственная, то вместо векторного уравнения (в) составляется три скалярных уравнения проекций на оси х, у иг.

В условиях задач по динамике, имеющихся в учебниках или задачниках, очень часто вместо массы точки или тела задается их вес (в кГ). В таких случаях массу точки (тела) определить очень легко: числовое значение массы (в кг) можно считать равным числовому значению веса (в кГ), так как масса 1 кг весит 1 кГ.

Задача №1

Свободная материальная точка, вес которой 5 кГ, движется прямолинейно с ускорением 50 см/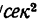. Определить силу, приложенную к точке.

Решение.

1.    Выразим значения обеих данных величин в единицах СИ. Так как точка весит 5 кГ, то ее масса т=5/сг, ускорение точки а = 50 см/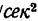 = 0,5 м/.

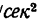2.    Согласно основному закону динамики,

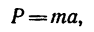
поэтому

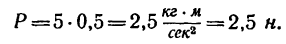
Таким образом, сила, сообщающая массе, равной 5 кг, ускорение 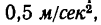равна 2,5 н, что соответствует 0,26 кГ, так как

• Заказать решение задач по теоретической механике

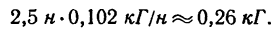
Задача №2

Свободная материальная точка находится под действием постоянной силы Р = 5,1 кГ в течение 20 сек и проходит за это время по прямолинейной траектории путь 0,5 км. До начала действия силы точка находится в покое Найти массу точки.

Решение 1—в единицах СИ.

1.    Выразим данные величины в единицах СИ: действующая сила Р = 5,1 кГ=5,1 *9,81 =50 н; время t=20 сек; пройденный путь s=0,5 км = 500 м. Так как точка начала движение из состояния покоя, то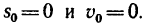

2.    Найдем ускорение точки. Сила постоянна, поэтому ускорение, приобретенное точкой, также постоянно и, следовательно, движение точки по прямолинейной траектории будет равнопеременным, т. е.

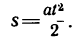
Отсюда

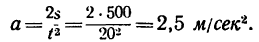
3.    Из основного закона динамики

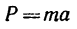
легко найти массу точки:

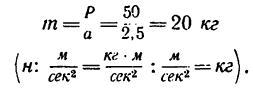
Решение 2 —в единицах МКГСС.

1.    Выразим величины в единицах технической системы: действующая сила Р=5,1 кГ; время t=20 сек; пройденный путь s=0,5 км =50 ) м.

2.    Ускорение определим так же, как и в первом решении:

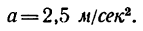
3.    Из основного закона динамики

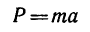
найдем массу точки:

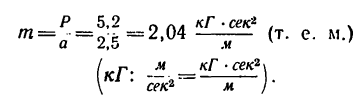
4.    Если перевести получившиеся 2,04 технической единицы массы в кг, то

2,04*9,81=20 кг.
Как видно, результаты обоих решении одинаковы.

Задача №3

Точка массой m=5 кг движется горизонтально по прямой АВ с ускорением а = 2 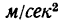, направленным вдоль той же прямой. Чему должны быть равны постоянные силы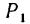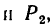лежащие в одной плоскости и действующие на точку, как показано на рис. 244.

Решение.

1.    На точку действуют две силы, сообщившие ей ускорение 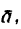числовое значение и направление которого известны. Поэтому векторное равенство (в) для дайной задачи примет вид

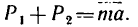
2.    Выбираем расположение осей координат, как показано на рис. 244. и, спроектировав векторное равенство на эти оси, получим два уравнения:

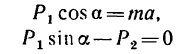
(вектор 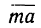направлен вдоль оси х и перпендикулярно к оси у, поэтому его проекция на ось х равна mа, а проекция на ось у равна нулю).

3.    Решаем получившуюся систему уравнений.

Из первого уравнения находим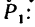

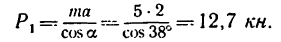
Из второго уравнения находим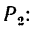

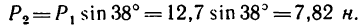
Задачу можно решить иначе. Сначала найти числовое значение равнодействующей сил 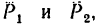воспользовавшись скалярным выражением уравнения (г):

R=ma.
Затем, зная, что вектор 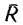совпадает по направлению с вектором 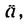по правилу параллелограмма разложить его на составляющие 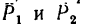и вычислить модули этих сил.