Движение горизонтально брошенного тела в физике - формулы и определение с примерами

Движение горизонтально брошенного тела:

Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой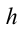

При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 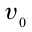. Поэтому перемещение
в горизонтальном направлении в любой момент времени 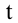, или длина полета, определяется следующей формулой: 

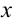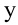Проекции скорости тела на оси и  определятся следующими соотношениями:

В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 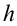. Следовательно, положение тела в вертикальном направлении после произвольного времени 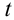будет определяться формулой:

Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 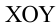будет иметь следующий вид:

Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 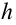, определяется выражением:

В этом случае формула для расчета длины полета тела будет иметь вид:

Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 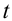) скорости в горизонтальном и вертикальном направлении будут  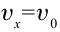и 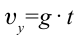соответственно. Таким образом, скорость тела при падении на землю определяется выражением:

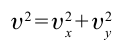
или

Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.

Образец решения задачи:

Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:

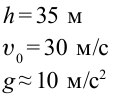
Найти:

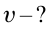
Формула:

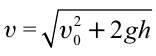
Решение:

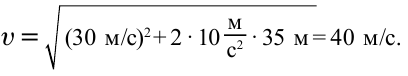
Ответ: 40 м/c.

Движение тела, брошенного горизонтально и под углом к горизонту

Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.

Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.

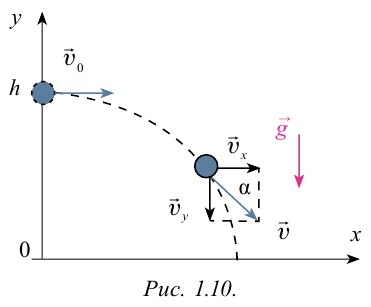
Рассмотрим движение тела, брошенного горизонтально со скоростью 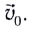Выберем систему координат так, что ее начало находится на поверхности Земли, направив ось Ох горизонтально, а ось Оу — вертикально (рис. 23).

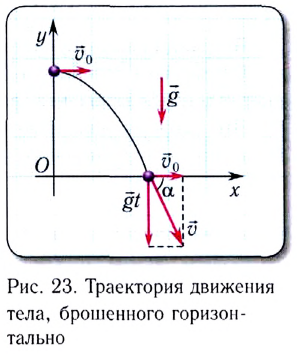
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 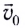 вдоль горизонта (оси Ох) и свободного падения в вертикальном направлении с ускорением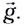

Движение тела в горизонтальном направлении будет описываться уравнением

а в вертикальном — уравнением

Здесь 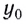— координата тела по оси Оу в начальный момент времени 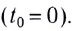Если тело брошено с высоты 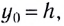то время падения 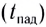определяется из

условия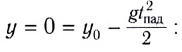

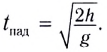
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем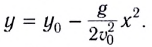

Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 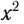отрицательный.

Скорость вдоль направления оси Ох остается неизменной и равной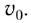

Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 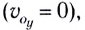поэтому мгновенная скорость вдоль оси Оу находится из соотношения 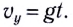Модуль мгновенной скорости определяется по теореме Пифагора (см. рис. 23):

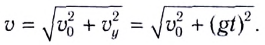
Угол между начальной скоростью 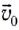и мгновенной скоростью и в момент времени t можно найти из соотношения

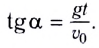
В приведенных формулах сопротивление воздуха не учитывается.

Рассмотрим теперь движение тела, брошенного со скоростью 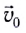под некоторым углом 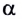к горизонту (рис. 24).

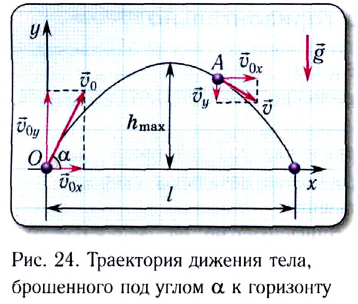
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью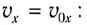

и равноускоренного в вертикальном направлении с ускорением 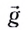и начальной
скоростью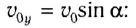

В том случае, если система координат выбрана так, что начальные координаты 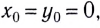уравнение траектории движения имеет вид

Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 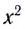отрицателен. Вершина параболы при этом имеет координаты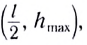

где l — дальность полета тела, 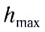— максимальная высота его подъема в процессе полета.

Модули горизонтальной 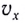 и вертикальной 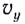составляющих мгновенной скорости 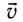движения определяются из следующих соотношений:

Мгновенную скорость 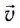 и движения тела в произвольной точке Л траектории можно найти как векторную сумму горизонтальной 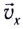и вертикальной 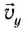мгновенных скоростей движения (см. рис. 24).

Время подъема тела можно найти из условия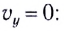

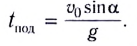
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 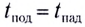(докажите это самостоятельно).

Таким образом, время полета тела можно найти как

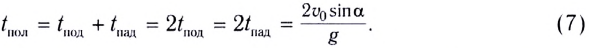
Определив вертикальную составляющую скорости 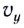 в искомый момент времeни, по формуле 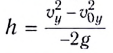можно найти высоту, на которой находится тело.

Максимальная высота подъема тела 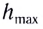легко определяется из условия, что вертикальная составляющая скорости в этой точке равна пулю 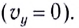Тогда

Дальность полета l — расстояние, пройденное телом за время полета 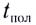 вдоль оси Ох с постоянной скоростью 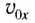(см. рис. 24). Она определяется по формуле

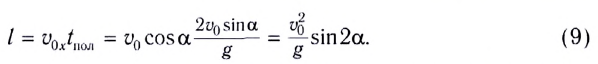
Таким образом, дальность полета определяется модулем начальной скорости 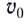тела и углом его бросания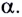

Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 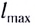полета достигается при 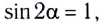т. е. при угле бросания 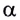= 45°.