Дуальные цепи

Дуальные цепи:

Под условием дуальности понимается такое соответствие электрических цепей, при котором закон изменения контурных токов в одной цепи подобен закону изменения узловых напряжений в другой цепи.

Для элементов электрической цепи, изображенных на рис. 7-26 (слева и справа), зависимости между напряжениями и токами имеют вид:

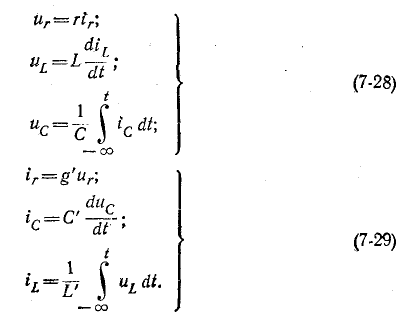
Следует иметь в виду, что входящие в уравнения (7-28) и (7-29) напряжения и токи, имеющие одинаковые буквенные обозначения, не равны друг другу.

Из сравнения уравнений (7-28) с уравнениями (7-29) видно, что условию дуальности удовлетворяют следующие элементы:

1. сопротивление и проводимость;
2. индуктивность и емкость;
3. источник э. д. с и источник тока.

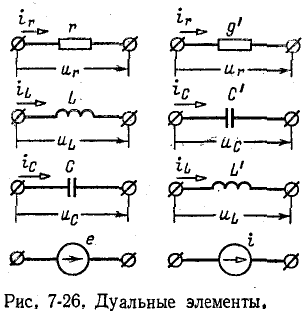
Элементы цепи, удовлетворяющие условию дуальности, называются аналогами или дуальными элементами.

При последовательном соединении элементов цепи 'суммируются напряжения, при параллельном соединении элементов цепи — токи. Поэтому последовательному соединению элементов соответствует параллельное соединение их аналогов, а параллельному соединению элементов — последовательное соединение их аналогов.

Например, при замене последовательно соединенных элементов r, LиС (рис. 7-27, а) их аналогами 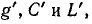соединенными параллельно (рис, 7-27, б), получаем дуальные цепи.

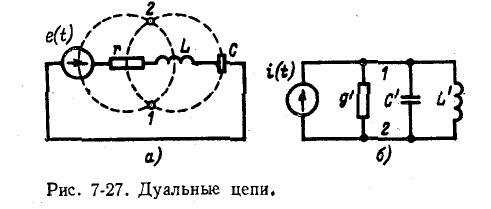
Уравнение напряжений для исходной цепи

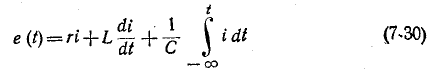
подобно уравнению токов для второй цепи

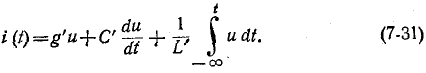
Контурному току i в уравнении (7-30) соответствует узловое напряжение и в уравнении (7-31),

Если э. д. с. и ток источников подчинены одному и тому же закону, например синусоидальны, и имеют одинаковую начальную фазу, то законы изменения контурного тока в схеме рис. 7-27, а и узлового напряжения в схеме рис, 7-27, 6 совпадают при соблюдении пропорции

В случае сложной электрической цепи каждой ее области, ограниченной независимым контуром, с учетом также области, внешней по отношению ко всей цепи, соответствует узел дуальной цепи. Следовательно, число областей заданной цепи равно числу узлов дуальной цепи.

При построении дуальной цепи по отношению к заданной планарной цепи удобно пользоваться следующим графическим приемом (рис. 7-27).

В каждой области, ограниченной независимым контуром заданной цепи, наносится точка, рассматриваемая в качестве будущего узла дуальной цепи.

Узлы, соответствующие каждой паре смежных областей, соединяются параллельными ветвями, число которых равно числу элементов, последовательно включенных в цепь, граничащую с указанными областями. Элементами параллельных ветвей являются аналоги элементов заданной цепи.

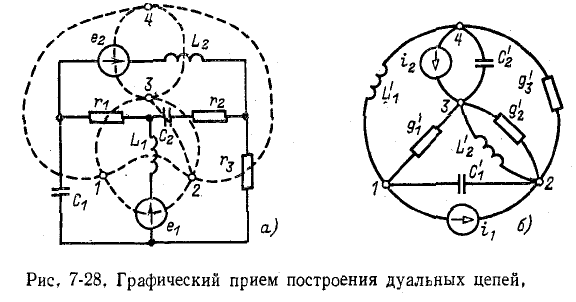
Графический способ построения дуальной цепи иллюстрирован ниже на примере рис. 7-28.

Исходная цепь (рис. 7-28, о) содержит три независимых контура. Внутри этих контуров фиксируем три точки (1, 2 и 3), соответствующие узлам исходной дуальной цепи. Четвертую точку, соответствующую узлу 4, фиксируем в области, внешней по отношению к заданной цепи. Проводим между этими точками пунктирные линии, пересекающие элементы цепи и представляющие собой ветви дуальной цепи; пересекаемые элементы заменяются их аналогами, включенными между соответствующими узлами дуальной цепи.

При согласовании направлений э. д. с. и токов дуальных источников руководствуются следующим правилом; если э. д. с. источника действует в положительном направлении контура (по ходу часовой

стрелки), то ток источника тока в дуальной цепи направлен к узлу, соответствующему данному контуру исходной схемы.

Следует заметить, что если графический способ построения дуальной цепи повторно применить к схеме рис, 7-28, б, то получится исходная схема рис. 7-28, а.

Существуют дуальные электрические цепи, имеющие одинаковую схему, например мостового типа (автодуальные схемы).

При соблюдении пропорции (7-32) комплексное сопротивление цепи, общей для двух смежных контуров схемы, пропорционально комплексной проводимости цепи, соединяющей два соответствующих узла дуальной цепи. Например, в схеме рис, 7-27, а комплексное сопротивление цепи равно:

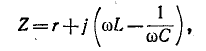
а в схеме рис, 7-28, б комплексная проводимость цепи

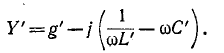
Полагая

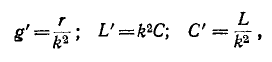
где k — коэффициент пропорциональности, имеющий размерность сопротивления, получаем;

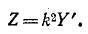
Аналогичная пропорциональность получается и между входным сопротивлением и проводимостью более сложных дуальных цепей. Это свойство используется, в частности, в теории электрических фильтров.