
Дробно-рациональные уравнения - примеры с решением
Дробно-рациональные уравнения — это уравнения c одной переменной.
Содержание:
Определение дробно-рационального уравнения
Определение дробно-рационального уравнения:
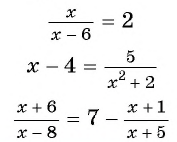
Например, уравнения
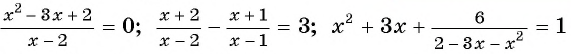
являются дробно-рациональными.
Рассмотрим дробно-рациональное уравнение 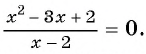 Это уравнение можно решить, используя условие равенства рациональной дроби нулю.
Это уравнение можно решить, используя условие равенства рациональной дроби нулю.
Рациональная дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю.
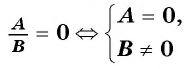
Таким образом, получим:
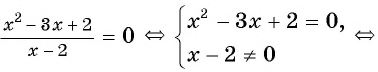
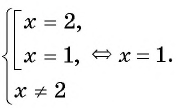
Ответ: 1.
Вернемся к уравнению 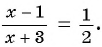 Выполним тождественные преобразования уравнения.
Выполним тождественные преобразования уравнения.
1) Перенесем все слагаемые из правой части уравнения в левую: 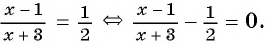
2) Преобразуем левую часть уравнения к рациональной дроби:
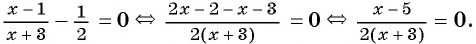
3) Применим условие равенства дроби нулю:
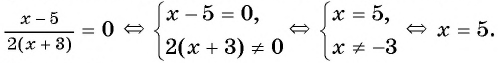
Ответ: 5.
Что нужно для решения дробно-рационального уравнения
Чтобы решить дробно-рациональное уравнение, нужно:
- Перенести все слагаемые из правой части уравнения в левую.
- Преобразовать левую часть уравнения к рациональной дроби.
- Применить условие равенства дроби нулю.
- Записать ответ.
Рассмотрим задачу: В дроби числитель на 2 больше знаменателя. Если числитель этой дроби уменьшить на 3, а знаменатель увеличить на 3, то новая дробь будет равна 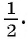 Найдите знаменатель первоначальной дроби.
Найдите знаменатель первоначальной дроби.
Решение:
Обозначим знаменатель первоначальной дроби через х, тогда ее числитель равен 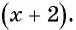
Если числитель дроби уменьшить на 3, то получится числитель новой дроби: 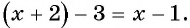 Знаменатель новой дроби после увеличения на 3 будет равен
Знаменатель новой дроби после увеличения на 3 будет равен 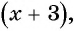 а новая дробь будет иметь вид
а новая дробь будет иметь вид 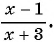 Так как по условию задачи она равна
Так как по условию задачи она равна 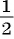 , то получим уравнение
, то получим уравнение 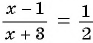 . В левой части этого уравнения записано дробное рациональное выражение.
. В левой части этого уравнения записано дробное рациональное выражение.
Решение многих задач приводит к уравнениям, у которых в левой или правой (или в той и другой) частях записаны дробные рациональные выражения. Такие уравнения называют дробно-рациональными уравнениями.
Пример №1
Решите уравнение 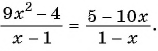
Решение:
(1) 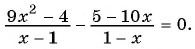
(2) 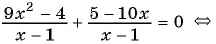
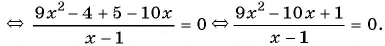
(3) 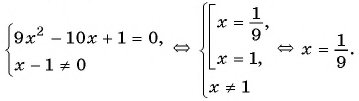
(4) Ответ: 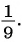
Пример №2
Решите уравнение
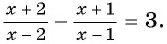
Решение:
(1) 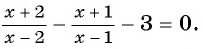
(2) 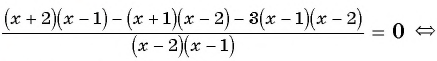
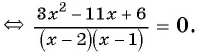
(3) 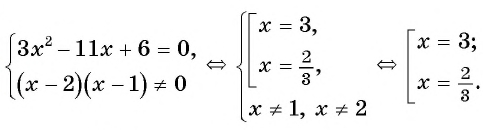
(4) Ответ: 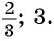
Пример №3
Решите уравнение
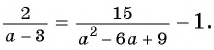
Решение:
(1) 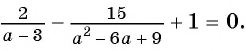
(2) 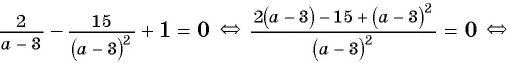
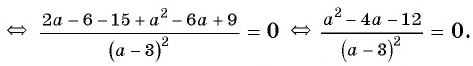
(3) 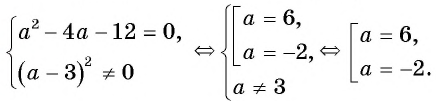
(4) Ответ: -2; 6.
Пример №4
Решите уравнение 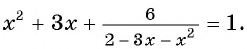
Решение:
Выполним замену переменной 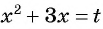 и получим уравнение
и получим уравнение 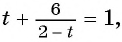 которое является дробно-рациональным. Решим его, применив алгоритм:
которое является дробно-рациональным. Решим его, применив алгоритм:
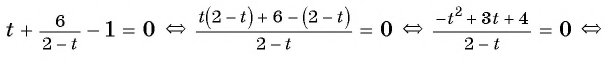
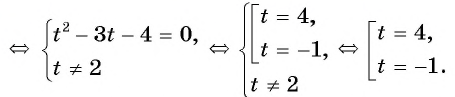
Подставим найденные значения 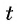 в равенство
в равенство 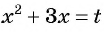 и получим:
и получим:
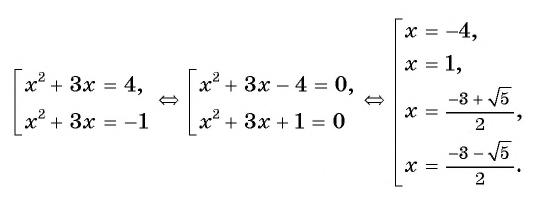
Ответ: 
Дробно-рациональные уравнения используются как математические модели для решения задач, описывающих реальные ситуации.
Например, рассмотрим задачу. На тушение лесных пожаров площадью 200 га отправлено несколько вертолетов с водосливными устройствами. По информации метеорологов предполагается усиление ветра, поэтому было выделено еще 5 вертолетов, в связи с чем площадь для сброса воды каждым вертолетом уменьшилась на 20 га. Сколько вертолетов участвовало в тушении пожаров первоначально?
Решение:
(1) Выясним, о каких величинах и зависимостях между ними в задаче идет речь. В задаче речь идет о площади лесных пожаров и количестве вертолетов для тушения пожаров.
(2) Выясним, какие значения, величин и зависимости между ними, известны. Известна зависимость между количеством вертолетов и площадью для сброса воды.
(3) Выясним, какие значения величин и зависимости между ними не известны. Неизвестно, сколько потребовалось вертолетов.
(4) Обозначим неизвестное значение одной величины через х, а остальные выразим через х и зависимости между величинами. Обозначим через 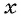 первоначальное количество вертолетов и получим, что
первоначальное количество вертолетов и получим, что 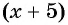 вертолетов направлено на тушение пожаров после сообщения метеорологов. Составим таблицу зависимостей между величинами.
вертолетов направлено на тушение пожаров после сообщения метеорологов. Составим таблицу зависимостей между величинами.
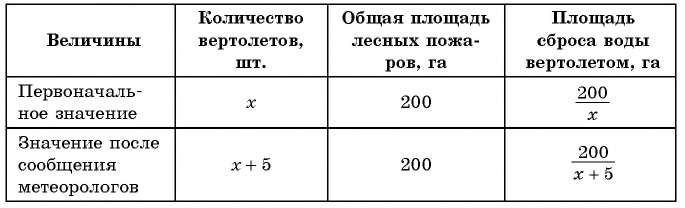
(5) Используя зависимости между известными и неизвестными значениями величин, составим уравнение (математическую модель задачи) и решим его.
По условию задачи 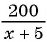 га на 20 га меньше, чем
га на 20 га меньше, чем 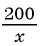 га. Значит, разность между большим и меньшим числом равна 20, т. е.
га. Значит, разность между большим и меньшим числом равна 20, т. е.
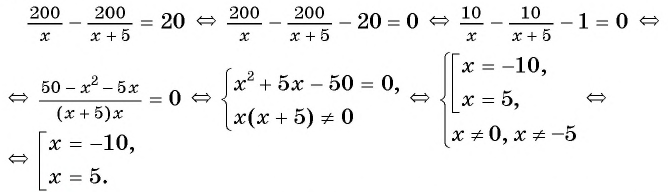
(6) Запишем ответ в соответствии со смыслом задачи. Поскольку 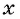 — число вертолетов, то выбираем число 5.
— число вертолетов, то выбираем число 5.
Ответ: 5 вертолетов.
Многие задачи, описывающие реальные процессы, имеют одну и ту же математическую модель. К таким относятся, например, задачи на движение, работу и т. п.
Рассмотрим две задачи:
Задача 1. Два велосипедиста выехали одновременно из поселка 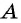 в поселок
в поселок 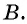 Скорость первого велосипедиста на
Скорость первого велосипедиста на 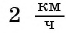 больше скорости второго, поэтому он прибыл в поселок
больше скорости второго, поэтому он прибыл в поселок 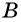 на 0,5 ч раньше. С какими скоростями двигались велосипедисты, если расстояние между поселками равно 30 км?
на 0,5 ч раньше. С какими скоростями двигались велосипедисты, если расстояние между поселками равно 30 км?
Задача 2. Для заполнения водой резервуара объемом 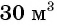 используют два крана: первый кран заполняет резервуар на 0,5 ч быстрее второго, так как в час через него наливается на
используют два крана: первый кран заполняет резервуар на 0,5 ч быстрее второго, так как в час через него наливается на 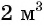 больше, чем через второй. Найдите скорость заполнения резервуара водой через каждый кран.
больше, чем через второй. Найдите скорость заполнения резервуара водой через каждый кран.
В обеих задачах речь идет о процессах: в первой — о процессе движения, во второй — о процессе заполнения резервуара водой.
Составим таблицу зависимостей между величинами.
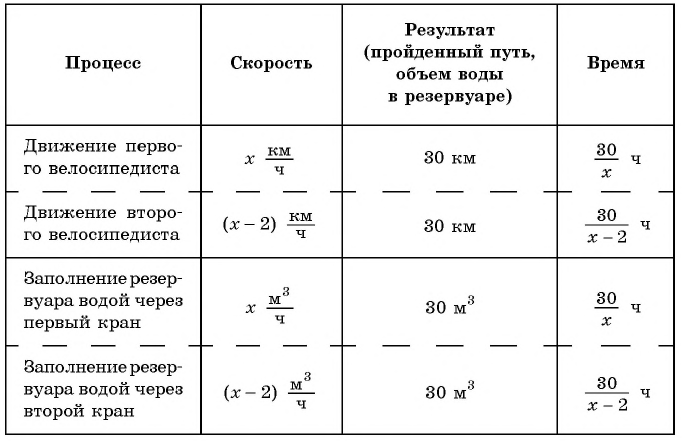
Поскольку первый велосипедист прибыл в поселок на 0,5 ч раньше второго, а один кран заполняет резервуар на 0,5 ч быстрее другого, то уравнение 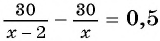 является математической моделью каждой из предложенных задач.
является математической моделью каждой из предложенных задач.
Решим полученное уравнение:
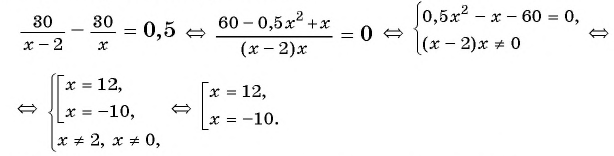
По условию каждой задачи подходит число 12.
Ответ задачи 1: скорость первого велосипедиста 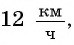 скорость второго велосипедиста
скорость второго велосипедиста 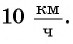 Ответ задачи 2: скорость заполнения резервуара водой через первый кран
Ответ задачи 2: скорость заполнения резервуара водой через первый кран 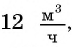 через второй кран —
через второй кран — 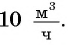
Пример №5
Является ли дробно-рациональным уравнение:
а) 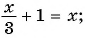
б) 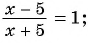
в) 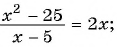
г) 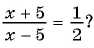
Решение:
Уравнение а) не является дробно-рациональным, так как его левая и правая части — целые рациональные выражения. Уравнения б)—г) являются дробно-рациональными, так как левые части этих уравнений — дробно-рациональные выражения.
Пример №6
Решите уравнение, используя условие равенства дроби нулю:
а) 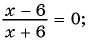
б) 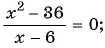
в) 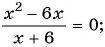
г) 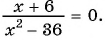
Решение:
а) 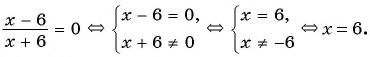
Ответ: 6.
б) 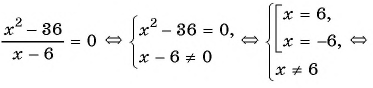
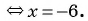
Ответ: -6.
в) 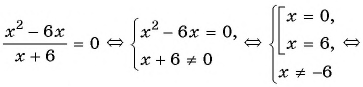
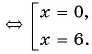
Ответ: 0; 6.
г) 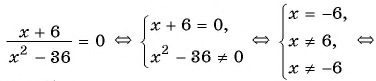
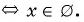
Ответ: нет корней.
Пример №7
Какие из уравнений:
а) 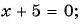
б) 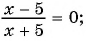
в) 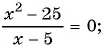
г) 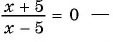 равносильны?
равносильны?
Решение:
а) 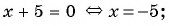
б) 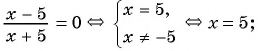
в) 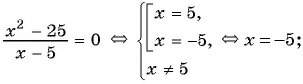
г) 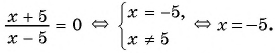
Ответ: уравнения а), в), г) имеют один и тот же корень (уравнения равносильны).
Пример №8
Решите уравнение:
а) 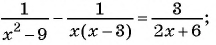
б) 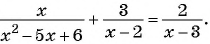
Решение:
а) (1) 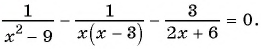
(2) 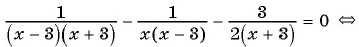
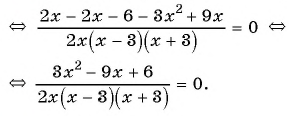
(3) 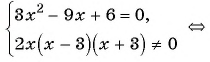
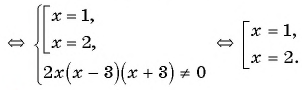
(4) Ответ: 1; 2.
б) 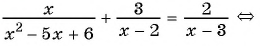
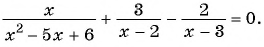
Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
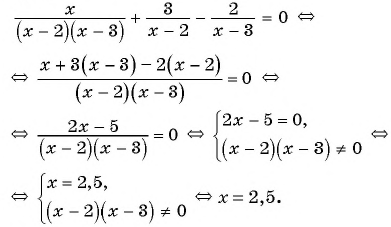
Ответ: 2,5.
Пример №9
Найдите нули функции
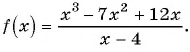
Решение:
Так как нули функции - это значения аргумента, при которых значение функции равно нулю, то для решения задачи нужно решить уравнение 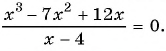
Используем условие равенства дроби нулю:
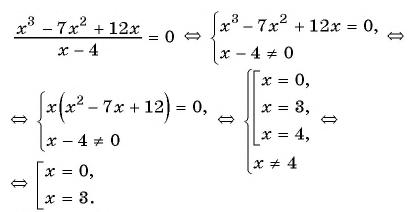
Ответ: 0; 3.
Пример №10
Найдите корни уравнения
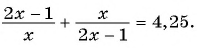
Решение:
Выполним замену переменной в данном уравнении: 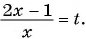 Получим уравнение
Получим уравнение 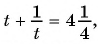 которое является дробно-рациональным.
которое является дробно-рациональным.
Решим его:
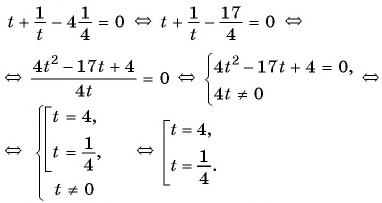
Выполним подстановку найденных значений переменной  и получим:
и получим:
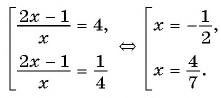
Ответ: 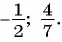
Моделирование реальных процессов с помощью дробно-рациональных уравнении
Задача:
Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Чему равна скорость катера при движении по озеру, если скорость течения реки 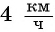 ?
?
Решение:
В задаче идет речь о процессах движения катера по реке и по озеру. Составим таблицу зависимостей между величинами.

Так как по условию задачи на весь путь затрачен 1 ч, то составим уравнение: 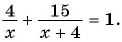 Решим его:
Решим его: 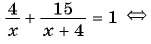
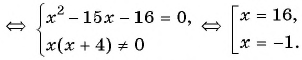
По условию подходит число 16.
Ответ: 16 
Системы нелинейных уравнений для решения дробно-рациональных уравнений
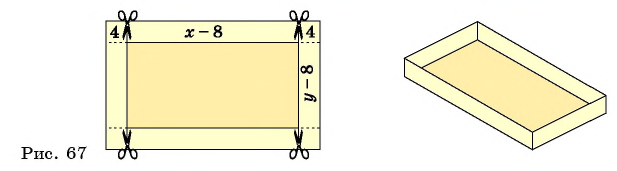
Рассмотрим задачу. Из листа картона прямоугольной формы нужно изготовить коробку без крышки, сделав надрезы в углах длиной 4 см (рис. 67). Найдите длину и ширину листа, зная, что его периметр равен 60 см, а объем коробки должен быть равен 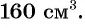
Решение:
Обозначим длину и ширину листа соответственно 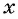 см и
см и 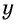 см. Так как в углах листа сделаны надрезы длиной 4 см, то высота коробки равна 4 см, а длина и ширина коробки равны
см. Так как в углах листа сделаны надрезы длиной 4 см, то высота коробки равна 4 см, а длина и ширина коробки равны 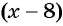 см и
см и  см соответственно.
см соответственно.
По условию задачи периметр листа прямоугольной формы равен 60 см, а объем коробки равен 160 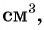 значит,
значит, 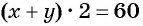 и
и 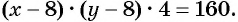 Оба полученных условия должны быть выполнены, поэтому объединим их в систему уравнений
Оба полученных условия должны быть выполнены, поэтому объединим их в систему уравнений 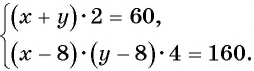
Полученная система уравнений содержит нелинейное рациональное уравнение 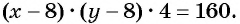 Такие системы называют системами нелинейных уравнений. Рассмотрим способы решения систем нелинейных уравнений.
Такие системы называют системами нелинейных уравнений. Рассмотрим способы решения систем нелинейных уравнений.
Способ подстановки
Решим полученную в задаче систему уравнений способом подстановки:
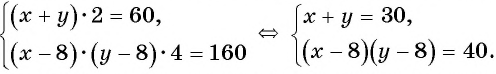
Из первого уравнения системы выразим переменную 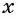 и получим
и получим 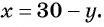
Заменим во втором уравнении переменную 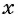 на
на 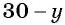 и получим уравнение
и получим уравнение 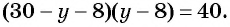 Решим это уравнение:
Решим это уравнение:
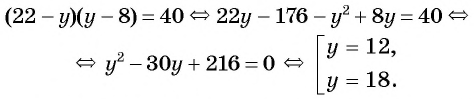
Найденные значения 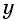 подставим в выражение
подставим в выражение 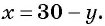 Тогда если
Тогда если 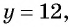 то
то 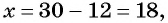 а если
а если 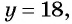 то
то 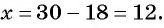
Решениями системы уравнений являются пары чисел 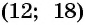 и
и 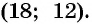 Таким образом, размер прямоугольного листа картона
Таким образом, размер прямоугольного листа картона 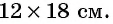
Чтобы решить систему уравнений способом подстановки, нужно:
- Из одного уравнения системы выразить одну из переменных.
- Заменить в другом уравнении эту переменную на ее выражение.
- Решить полученное уравнение.
- Найденные значения одной переменной подставить в выражение для другой переменной и найти значение другой переменной.
- В виде упорядоченных пар чисел записать ответ.
Решите систему уравнений
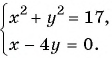
Решение:
(1) Из второго уравнения системы выразим переменную 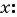
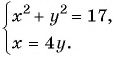
(2) Заменим в первом уравнении переменную 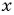 на
на 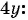
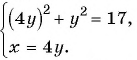
(3) Решим уравнение 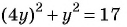 и получим:
и получим: 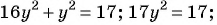
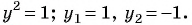
(4) Найденные значения 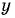 подставим в выражение
подставим в выражение 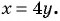
Если 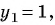 то
то 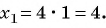
Если 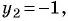 то
то 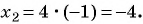
(5) Ответ: (4; 1), (-4; -1).
Способ сложения
Чтобы решить систему уравнений способом сложения, нужно:
- Одно из уравнений системы оставить без изменения, а другое заменить суммой уравнений системы.
- Из полученного уравнения (суммы) найти значения одной из переменных.
- Подставить эти значения переменной в оставленное без изменения уравнение системы и найти значения другой переменной.
- Записать ответ.
Решите систему уравнений
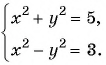
Решение:
(1) 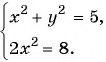
(2) 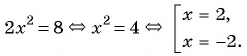
(3) При 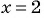 получим:
получим:
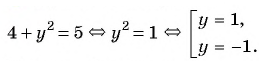
При 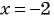 получим:
получим:
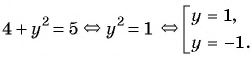
(4) Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
Графический метод решения систем нелинейных уравнений
Решим систему уравнений 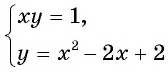 графическим методом. Для этого построим в одной системе координат графики каждого из уравнений системы.
графическим методом. Для этого построим в одной системе координат графики каждого из уравнений системы.
Первое уравнение системы равносильно уравнению 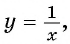 графиком которого является гипербола, проходящая через точки (1; 1), (0,5; 2) (рис. 68).
графиком которого является гипербола, проходящая через точки (1; 1), (0,5; 2) (рис. 68).
Графиком второго уравнения системы 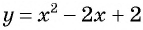 является парабола с вершиной в точке (1; 1), пересекающая ось ординат в точке (0; 2).
является парабола с вершиной в точке (1; 1), пересекающая ось ординат в точке (0; 2).
Единственная точка пересечения гиперболы 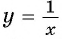 и параболы
и параболы 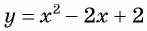 имеет координаты (1; 1).
имеет координаты (1; 1).
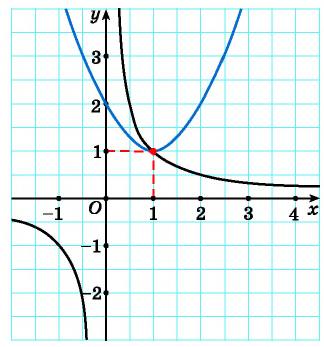
Рис. 68
Поскольку графический метод решения систем уравнений не является точным, то полученный результат необходимо проверить.
Подставим пару чисел (1; 1) в каждое из уравнений системы 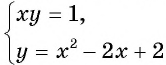 , и получим верные равенства. Таким образом, данная система имеет единственное решение (1; 1).
, и получим верные равенства. Таким образом, данная система имеет единственное решение (1; 1).
В рассмотренной системе решением оказалась пара целых чисел, которую легко было найти с помощью построенных графиков. В других случаях найти точные значения переменных по графику может оказаться затруднительно. Но, как правило, с помощью графического метода можно определить число решений системы уравнений.
Например, определим число решений системы уравнений 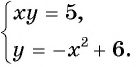 Построим в одной системе координат графики каждого из уравнений системы (рис. 69). Графиком первого уравнения системы является гипербола, проходящая через точки (1; 5), (5; 1). Графиком второго уравнения - парабола, ветви которой направлены вниз, с вершиной в точке (0; 6). Графики пересекаются в трех точках, значит, система уравнений имеет три решения.
Построим в одной системе координат графики каждого из уравнений системы (рис. 69). Графиком первого уравнения системы является гипербола, проходящая через точки (1; 5), (5; 1). Графиком второго уравнения - парабола, ветви которой направлены вниз, с вершиной в точке (0; 6). Графики пересекаются в трех точках, значит, система уравнений имеет три решения.
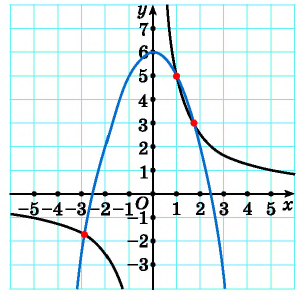
Рис. 69
Моделирование реальных процессов с помощью систем нелинейных уравнений
Системы нелинейных уравнений также являются математическими моделями при решении задач.
Задача:
Лечебными травами было решено засеять прямоугольный участок площадью 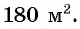 При вспашке участка одну его сторону уменьшили на 3 м, а другую — на 2 м. Его площадь стала равна
При вспашке участка одну его сторону уменьшили на 3 м, а другую — на 2 м. Его площадь стала равна 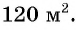 Какими были первоначальные размеры участка?
Какими были первоначальные размеры участка?
Решение:
В задаче речь идет о длине и ширине прямоугольного участка и его площади.
Если одну сторону участка обозначить через 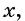 а другую — через
а другую — через 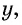 то планируемая площадь участка равна
то планируемая площадь участка равна 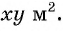 По условию она равна
По условию она равна 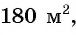 значит, получится уравнение
значит, получится уравнение 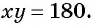
После уменьшения размеров участка площадь станет равной 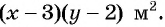 По условию задачи составим уравнение
По условию задачи составим уравнение 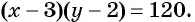
Объединим оба уравнения в систему 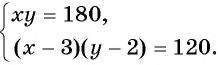
Получили математическую модель задачи в виде системы нелинейных уравнений. Решим ее, используя способ подстановки.
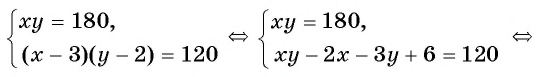
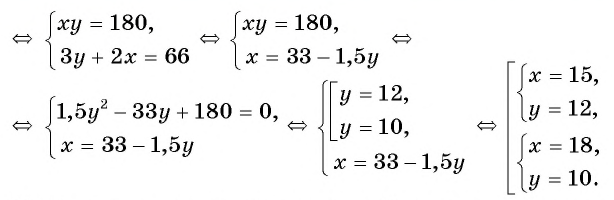
Условию задачи удовлетворяют найденные решения системы: стороны участка равны либо 15 м и 12 м, либо 18 м и 10 м.
Ответ: 15 м, 12 м или 18 м, 10 м.
Пример №11
Решите систему уравнений:
а) 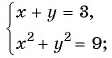
б) 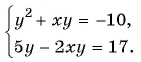
Решение:
а) Решим систему способом подстановки:
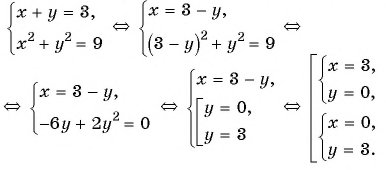
Ответ: (3; 0), (0; 3).
б) Применим способ сложения. Умножим первое уравнение на 2, сложим со вторым и получим:
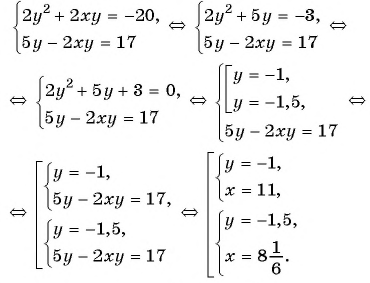
Ответ: 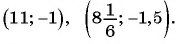
Пример №12
Решите графически систему уравнений
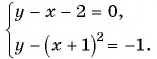
Решение:
Построим графики уравнений системы
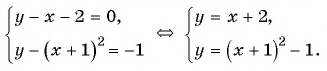
График первого уравнения — прямая, проходящая через точки (-2; 0), (1; 3). График второго уравнения — парабола с вершиной в точке (-1; -1), пересекающая ось абсцисс в точках (-2; 0) и (0; 0), проходящая через точку (1; 3). 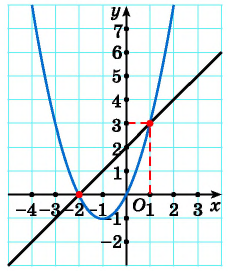
Прямая пересекается с параболой в точках с координатами (-2; 0), (1; 3). С помощью проверки убеждаемся, что пары чисел (-2; 0) и (1; 3) являются решениями данной системы.
Ответ: (-2; 0), (1; 3).
Пример №13
Сколько решений имеет система уравнений 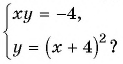
Решение:
Построим в одной системе координат графики уравнений системы. Графиком первого уравнения системы является гипербола, проходящая через точки (-1; 4), (-4; 1). График второго уравнения — парабола с вершиной в точке (-4; 0), пересекающая ось ординат в точке (0; 16).
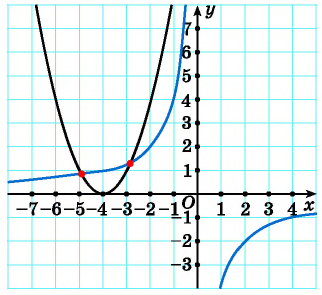
На рисунке видны только две точки пересечения графиков. Но, учитывая то, что парабола пересекает ось ординат, а гипербола не пересекает, делаем вывод, что графики пересекаются еще в одной точке. Таким образом, графики пересекаются в трех точках, а, значит, система имеет три решения.
Пример №14
Решите систему уравнений
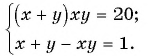
Решение:
Решим систему методом замены переменных. Введем новые переменные: 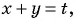
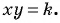
Тогда система примет вид 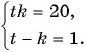
Решим ее способом подстановки:
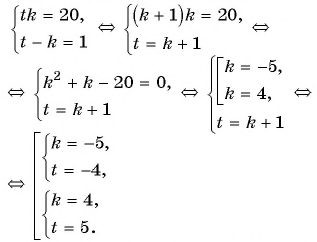
Подставим 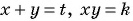 и получим:
и получим:
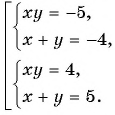
Решив каждую из двух систем совокупности способом подстановки, получим следующие решения исходной системы уравнений: (-5; 1); (1; -5); (4; 1); (1; 4).
Ответ: (-5; 1); (1; -5); (4; 1); (1; 4).
Задача:
Сумма квадратов цифр двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
Решение:
Обозначим цифру десятков данного числа через 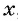 , а цифру единиц через
, а цифру единиц через 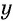 , тогда данное число будет иметь вид
, тогда данное число будет иметь вид 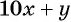 . Числом, записанным теми же цифрами, но в обратном порядке, будет
. Числом, записанным теми же цифрами, но в обратном порядке, будет 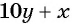 . По условию задачи:
. По условию задачи: 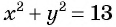 и
и 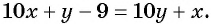 Составим и решим систему уравнений:
Составим и решим систему уравнений:
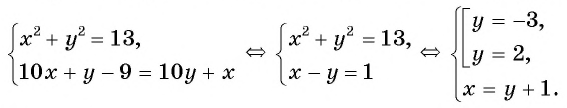
По условию задачи подходит только 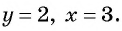
Ответ: 32.
Задача:
Из поселка 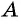 в поселок
в поселок 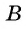 вышел пешеход. Одновременно с ним из поселка
вышел пешеход. Одновременно с ним из поселка 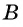 в поселок
в поселок 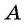 выехал велосипедист. Через 50 мин они встретились. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из
выехал велосипедист. Через 50 мин они встретились. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из 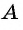 в
в 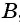 , если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода?
, если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода?
Решение:
Составим таблицу зависимостей между величинами.
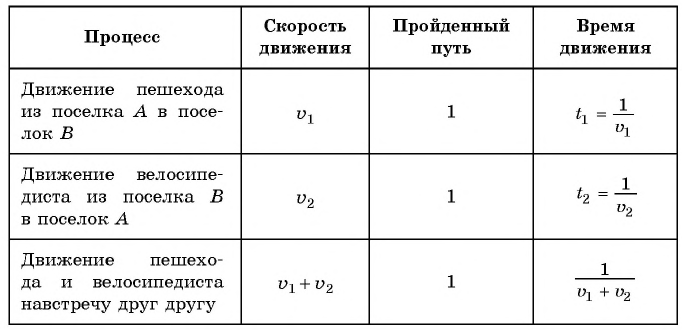
По условию задачи велосипедист проделал бы тот же путь на 4 ч быстрее пешехода, поэтому получим уравнение 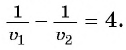
При движении навстречу друг другу пешеход и велосипедист встретились через 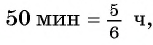 т. е.
т. е. 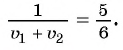
Составим и решим систему уравнений:
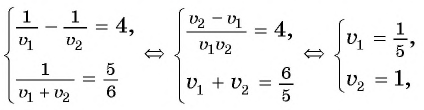 откуда
откуда 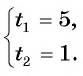
Ответ: 5 ч.
Задача:
Две бригады, работая вместе, ремонтировали дорогу в течение б дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на б дней быстрее, чем одна вторая?
Решение:
Составим таблицу зависимостей между величинами.
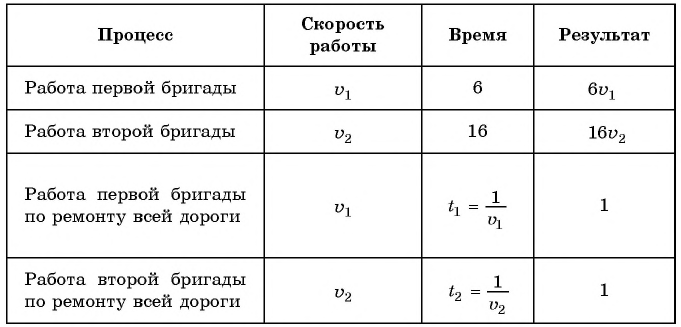
Обозначим объем всей работы через 1, тогда получим уравнение 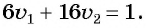
Зная, что одна первая бригада может выполнить эту работу на б дней быстрее, чем одна вторая, составим уравнение 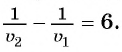
Составим и решим систему уравнений: 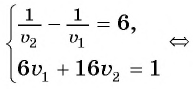
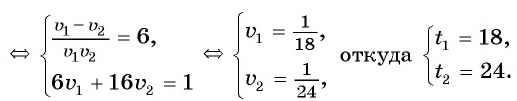
Ответ: 18 ч.
Формула длины отрезка с заданными координатами его концов. Уравнение окружности
Для применения графического метода решения систем необходимо знать графики различных уравнений. Многие из них вам уже знакомы. Это, например, прямая, гипербола, парабола.
Расширим возможности использования графического метода решения систем нелинейных уравнений и выведем уравнение окружности с центром в заданной точке с заданным радиусом. Для этого сначала выведем формулу для вычисления длины отрезка с заданными координатами его концов, т. е. для вычисления расстояния между двумя точками, заданными своими координатами.
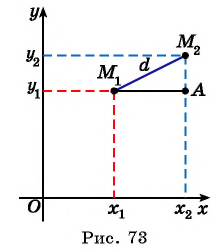
Рассмотрим точки 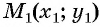 и
и 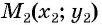 (рис. 73). Найдем расстояние
(рис. 73). Найдем расстояние 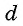 между этими точками (длину отрезка
между этими точками (длину отрезка 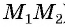 ). Рассмотрим прямоугольный треугольник
). Рассмотрим прямоугольный треугольник 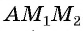 , в котором
, в котором 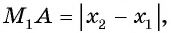
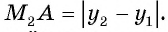 По теореме Пифагора найдем гипотенузу треугольника
По теореме Пифагора найдем гипотенузу треугольника 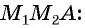
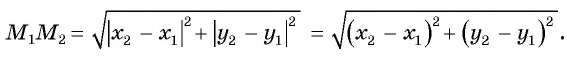
Получили формулу длины отрезка с заданными координатами его концов, или формулу расстояния между двумя точками с координатами 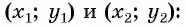
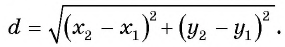
Пример №15
Найдите расстояние между точками А(-1; 3) и В(2; 5).
Решение:
Подставим координаты точек А(-1; 3) и В(2; 5) в формулу расстояния между двумя точками 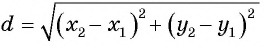 и получим, что
и получим, что
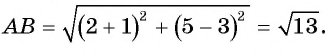
Рассмотрим окружность на координатной плоскости. Окружность — это множество точек плоскости, расстояние от каждой из которых до одной данной точки (центра окружности) является величиной постоянной, равной радиусу окружности 
По формуле расстояния между двумя точками найдем расстояние от данной точки 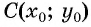 (центра окружности) до произвольной точки окружности
(центра окружности) до произвольной точки окружности 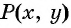 (рис. 74):
(рис. 74):
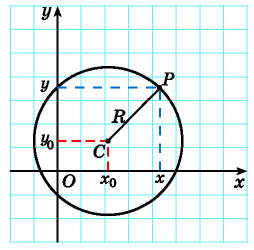
Рис. 74
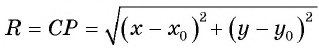 или
или 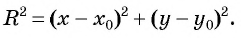
Таким образом, если точка принадлежит окружности с центром 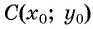 и радиусом
и радиусом 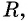 то ее координаты удовлетворяют уравнению
то ее координаты удовлетворяют уравнению 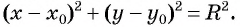
Уравнение 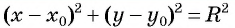 является уравнением окружности с центром в точке
является уравнением окружности с центром в точке 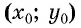 и радиусом
и радиусом 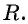
Если координаты точки удовлетворяют уравнению 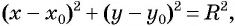 то эта точка принадлежит окружности с центром
то эта точка принадлежит окружности с центром 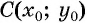 и радиусом
и радиусом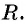
Покажем, что если точка 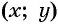 не принадлежит окружности с центром
не принадлежит окружности с центром 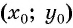 и радиусом
и радиусом 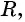 то ее координаты не удовлетворяют уравнению
то ее координаты не удовлетворяют уравнению 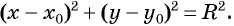 Действительно, если точка лежит вне окружности, то расстояние от нее до центра окружности больше радиуса, т. е.
Действительно, если точка лежит вне окружности, то расстояние от нее до центра окружности больше радиуса, т. е. 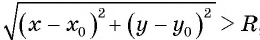 , а если точка лежит внутри окружности, то меньше,
, а если точка лежит внутри окружности, то меньше,
т. е. 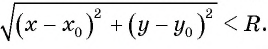
Чтобы составить уравнение окружности, нужно:
- Определить координаты центра окружности
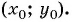
- Определить радиус окружности
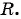
- Подставить найденные значения
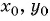 и
и 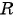 в уравнение окружности
в уравнение окружности 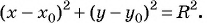
Составьте уравнение окружности с центром в точке (-8; 2) и радиусом 5.
Решение:
(1) 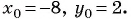
(2) 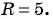
(3) 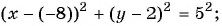
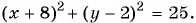
Пример №16
Составьте уравнение окружности:
а) с центром в точке (4; -1) и радиусом 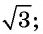
б) с центром в точке (0; 0) и радиусом 4.
Решение:
а) Подставим координаты центра окружности 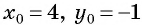 и значение радиуса
и значение радиуса 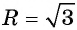 в уравнение окружности
в уравнение окружности 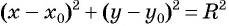 и получим
и получим 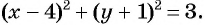
б) Координаты центра окружности: 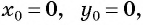 радиус окружности
радиус окружности 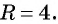 Тогда уравнение данной окружности
Тогда уравнение данной окружности 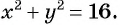
Если центром окружности радиуса 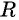 является начало координат, то ее уравнение имеет вид
является начало координат, то ее уравнение имеет вид 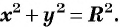
Пример №17
Определите количество решений системы уравнений 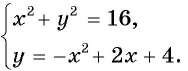
Решение:
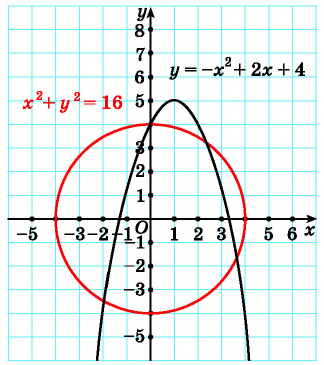
Рис. 75
Построим графики уравнений системы. Первое уравнение — это уравнение окружности с центром в начале координат и радиусом, равным 4. Графиком второго уравнения является парабола с вершиной в точке (1; 5), пересекающая ось ординат в точке (0; 4).
Построенные графики пересекаются в четырех точках (рис. 75). Значит, данная система уравнений имеет 4 решения.
Ответ: 4 решения.
Пример №18
Найдите длину отрезка 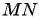 , если
, если 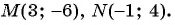
Решение:
По формуле длины отрезка 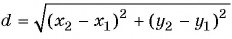 получим:
получим: 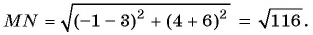
Пример №19
Найдите длину диагонали прямоугольника, если заданы его вершина 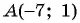 и точка пересечения его диагоналей
и точка пересечения его диагоналей 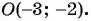
Решение:
Найдем длину отрезка 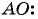
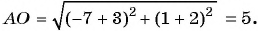
Длина отрезка 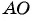 равна половине диагонали прямоугольника, следовательно, длина диагонали равна 10.
равна половине диагонали прямоугольника, следовательно, длина диагонали равна 10.
Пример №20
Определите координаты центра и радиус окружности:
а) 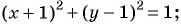
б) 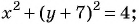
в) 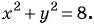
Решение:
а) 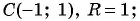
б) 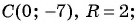
в) 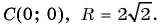
Пример №21
Какие из данных точек лежат на окружности 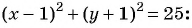
а) 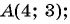
б) 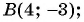
в) 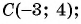
г) 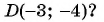
Решение:
Подставим координаты точек в уравнение окружности:
а) 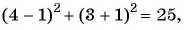 равенство верное, значит, точка
равенство верное, значит, точка 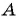 лежит на окружности; б)
лежит на окружности; б) 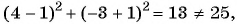 значит, точка
значит, точка 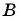 не лежит на окружности;
не лежит на окружности;
в) 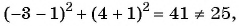 значит, точка
значит, точка 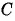 не лежит на окружности;
не лежит на окружности;
г) 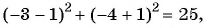 равенство верное, значит, точка
равенство верное, значит, точка 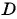 лежит на окружности.
лежит на окружности.
Пример №22
Запишите уравнение окружности с центром в точке (-1; 1) и радиусом 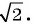
Решение:
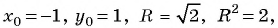
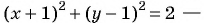 уравнение окружности.
уравнение окружности.
Пример №23
Запишите уравнение окружности с центром в точке 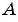 , для которой отрезок
, для которой отрезок 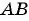 является радиусом, если А(2; 4), В(5; 7).
является радиусом, если А(2; 4), В(5; 7).
Решение:
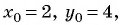 радиус найдем по формуле расстояния между двумя точками:
радиус найдем по формуле расстояния между двумя точками: 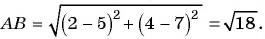
Уравнение окружности 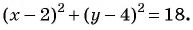
Пример №24
Решите систему уравнений 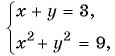 используя графический метод.
используя графический метод.
Решение:
График первого уравнения — прямая, проходящая через точки (3; 0), (0; 3). График второго уравнения — окружность с центром в начале координат и радиусом, равным 3.
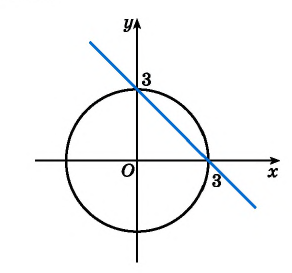
Координаты точек пересечения (3; 0), (0; 3) — решения системы.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |