
Дробно-рациональные неравенства - примеры с решением
Рациональным называется неравенство, в левой и правой частях которого — рациональные выражения.
Содержание:
Задача:
Лодка прошла по течению реки 5 км и вернулась обратно, затратив на весь путь не больше 1 ч. Какова наименьшая возможная скорость лодки, если скорость течения реки равна 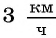
Решение:
Обозначим через 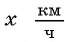

По условию задачи на весь путь лодка затратила не больше 1 ч. Составим математическую модель: 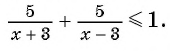
Полученное в ходе решения задачи неравенство 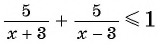 является рациональным.
является рациональным.
Метод интервалов для решения дробно-рациональных неравенств
Рассмотрим один из методов решения рациональных неравенств — метод интервалов. Этот метод основан на использовании графика функции.
Предположим, что нужно решить неравенство 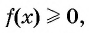 где
где 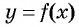 — функция, график которой изображен на рисунке 80. Тогда для решения неравенства
— функция, график которой изображен на рисунке 80. Тогда для решения неравенства 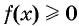 достаточно указать значения аргумента, при которых значения функции
достаточно указать значения аргумента, при которых значения функции 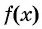 неотрицательны, т. е. при которых график функции лежит не ниже оси абсцисс. Это промежутки [-6; -2] и [2; 8]. Следовательно, все решения неравенства
неотрицательны, т. е. при которых график функции лежит не ниже оси абсцисс. Это промежутки [-6; -2] и [2; 8]. Следовательно, все решения неравенства 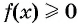 — это все
— это все
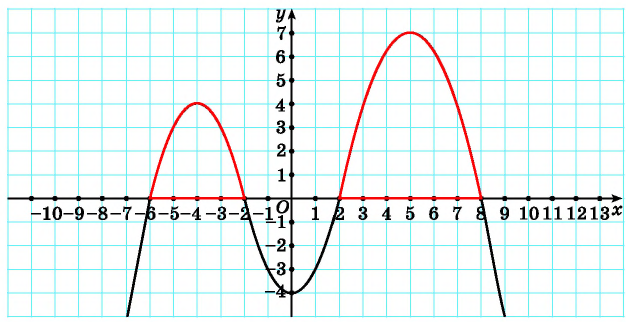
Рис. 80
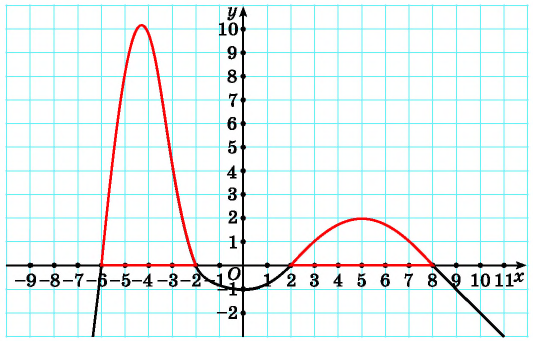
Рис. 81
значения переменной 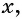 принадлежащие объединению множеств
принадлежащие объединению множеств 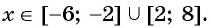
Заметим, что такие же решения имеет неравенство 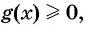 — функция, график которой изображен на рисунке 81, так как значения функции
— функция, график которой изображен на рисунке 81, так как значения функции 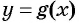 неотрицательны при тех же значениях переменной, что у функции
неотрицательны при тех же значениях переменной, что у функции 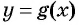 .
.
Таким образом, для применения метода интервалов к решению неравенства достаточно построить схему графика функции, на которой отражены только некоторые (необходимые для решения неравенства) свойства функции, а именно ее область определения, нули и промежутки знакопостоянства.
Примеры с решением
Пример №1
Решите неравенство
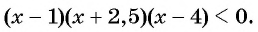
Решение:
Рассмотрим функцию 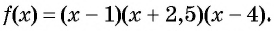 Построим схему графика этой функции, по которой определим ее промежутки знакопостоянства. Для этого найдем точки пересечения графика с осью абсцисс, т. е. нули этой функции:
Построим схему графика этой функции, по которой определим ее промежутки знакопостоянства. Для этого найдем точки пересечения графика с осью абсцисс, т. е. нули этой функции: 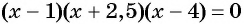 при
при 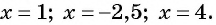
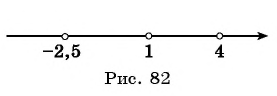
Отметим нули функции на оси абсцисс (рис. 82). Так как данное неравенство строгое, то нули функции отметим на оси пустыми точками.
Нули функции разбили ось на четыре промежутка. Определим, выше или ниже оси абсцисс расположен график функции в каждом из полученных промежутков.
Поскольку правее точки 4 каждый из трех множителей произведения 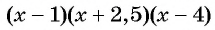 принимает положительные значения, то при
принимает положительные значения, то при 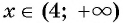 график функции
график функции 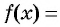
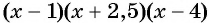 расположен выше оси абсцисс.
расположен выше оси абсцисс.
При переходе через каждую из отмеченных точек знак функции 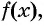 а значит, и положение графика относительно оси абсцисс меняется, так как меняется знак одного из множителей.
а значит, и положение графика относительно оси абсцисс меняется, так как меняется знак одного из множителей.
Построим схему графика функции 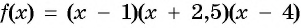 (рис. 83).
(рис. 83).
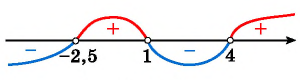
Рис. 83
При 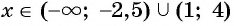 построенная кривая лежит ниже оси абсцисс. Это объединение интервалов является множеством решений данного неравенства.
построенная кривая лежит ниже оси абсцисс. Это объединение интервалов является множеством решений данного неравенства.
Ответ: 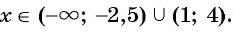
Пример №2
Решите неравенство
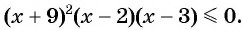
Решение:
Рассмотрим функцию 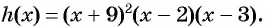 Найдем ее нули:
Найдем ее нули: 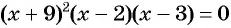 при
при 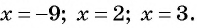 Так как неравенство нестрогое, то нули функции являются решениями данного неравенства, поэтому включим их во множество решений неравенства и отметим на оси абсцисс закрашенными точками (рис. 84).
Так как неравенство нестрогое, то нули функции являются решениями данного неравенства, поэтому включим их во множество решений неравенства и отметим на оси абсцисс закрашенными точками (рис. 84).
Затем определим положение графика функции в каждом из четырех полученных промежутков. Правее точки 3 каждый из трех множителей произведения 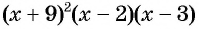 принимает положительные значения, значит, график функции расположен выше оси абсцисс. При переходе через точки 3 и 2 положение графика меняется, так как меняется знак одного из множителей
принимает положительные значения, значит, график функции расположен выше оси абсцисс. При переходе через точки 3 и 2 положение графика меняется, так как меняется знак одного из множителей 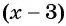 или
или 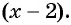 При переходе через точку -9 положение графика не меняется, так как множитель
При переходе через точку -9 положение графика не меняется, так как множитель 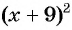 принимает неотрицательные значения при всех
принимает неотрицательные значения при всех 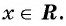
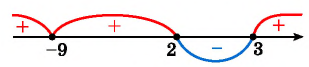
Рис. 84
Построим схему графика функции (см. рис. 84) и запишем решение неравенства в соответствии с его знаком: 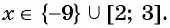
Ответ: 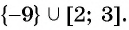
Если во множителе число 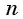 — четное, то при переходе через точку а положение графика относительно оси абсцисс не меняется, а если число
— четное, то при переходе через точку а положение графика относительно оси абсцисс не меняется, а если число 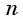 — нечетное, то меняется.
— нечетное, то меняется.
Пример №3
Решите неравенство 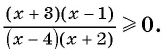
Решение:
Рассмотрим функцию 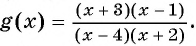
Отметим на оси абсцисс нули этой функции (числа -3 и 1) и те значения переменной, которые не входят в область определения функции 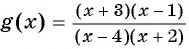 (это числа -2 и 4 - значения переменной, при которых знаменатель дроби обращается в нуль (нули знаменателя) (рис. 85).
(это числа -2 и 4 - значения переменной, при которых знаменатель дроби обращается в нуль (нули знаменателя) (рис. 85).
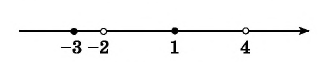
Рис. 85
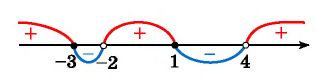
Рис. 86
Так как неравенство нестрогое, то нули функции являются решениями неравенства (на оси абсцисс — закрашенные точки -3 и 1). Нули знаменателя не являются решениями неравенства (на оси абсцисс — пустые точки -2 и 4).
Построим схему графика (рис. 86). Положение графика относительно оси абсцисс меняется при переходе через каждую точку. По схеме графика в соответствии со знаком неравенства запишем его решение: 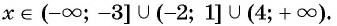
Ответ: 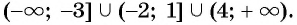
Для того чтобы решить рациональное неравенство методом интервалов, нужно:
- Привести неравенство к виду
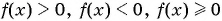 или
или 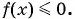
- Найти и отметить на оси абсцисс нули функции и те значения переменной, при которых значения функции не существуют (нули знаменателя).
- Построить схему графика функции.
- Записать ответ в соответствии со знаком неравенства.
Решите неравенство
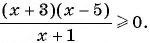
Решение:
(1) Неравенство имеет вид 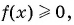 где
где 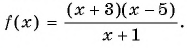
(2) 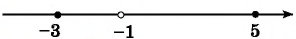
(3) 
(4) Ответ: 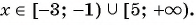
Пример №4
Решите неравенство 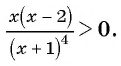
Решение:
(1) Неравенство имеет вид 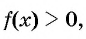 где
где 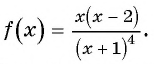
(2) Найдем нули функции (числа 0; 2) и, поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками. Найдем значение переменной, при котором значения функции не существуют, — нуль знаменателя (число -1) и отметим его на оси абсцисс пустой точкой (рис. 87).
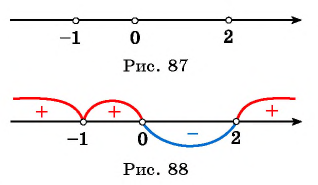
(3) Построим схему графика функции, при этом учтем, что при переходе через точку -1 положение графика относительно оси не меняется, а при переходе через точки 0 и 2 меняется (рис. 88).
(4) Ответ: 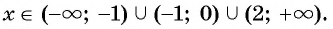
Для того чтобы положение графика в первом правом промежутке было выше оси абсцисс, нужно умножением обеих частей неравенства на -1 добиться положительных коэффициентов перед переменной в линейных множителях.
Пример №5
Решите неравенство 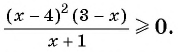
Решение:
Для того чтобы все коэффициенты перед переменными в линейных множителях были положительными, умножим обе части неравенства 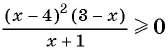 на -1 и получим неравенство
на -1 и получим неравенство 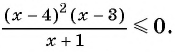
(1) Неравенство имеем вид 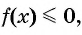 где
где 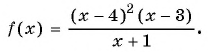
(2) Найдем нули функции (числа 3 и 4) и, поскольку знак неравенства нестрогий, отметим их на оси абсцисс закрашенными точками. Найдем значение переменной, при котором значение функции не существует (число -1), и отметим его на оси абсцисс пустой точкой (рис. 89).

Рис. 89
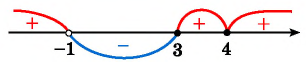
Рис. 90
(3) Построим схему графика функции, при этом учтем, что при переходе через точку 4 положение графика относительно оси не меняется, а при переходе через точки -1 и 3 меняется (рис. 90).
(4) Ответ: 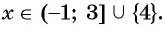
Пример №6
Какие из следующих неравенств являются рациональными:
а) 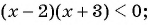
б) 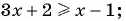
в) 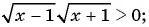
г) 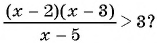
Решение:
Неравенства а), б), г) — рациональные, так как в левой и правой частях этих неравенств — рациональные выражения. Неравенство в) не является рациональным, так как содержит иррациональные выражения с переменной.
Пример №7
Решите неравенство:
а) 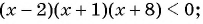
б) 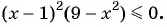
Решение:
а) (1) Неравенство имеет вид 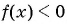 , где
, где 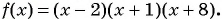
(2) Нулями функции являются числа -8; —1 и 2. Поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками.

(3) Построим схему графика функции. При переходе через каждую из точек -8; -1 и 2 положение графика относительно оси меняется.
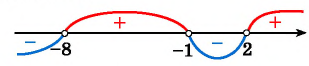
(4) Ответ: 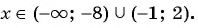
б) Умножим обе части данного неравенства на -1 и получим неравенство 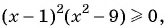 которое запишем в виде
которое запишем в виде 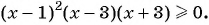 Нулями функции
Нулями функции 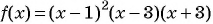 являются числа -3; 1 и 3. Так как знак неравенства нестрогий, то на оси абсцисс числа -3; 1 и 3 отметим закрашенными точками. Построим схему графика функции.
являются числа -3; 1 и 3. Так как знак неравенства нестрогий, то на оси абсцисс числа -3; 1 и 3 отметим закрашенными точками. Построим схему графика функции.

При переходе через точку 1 положение графика относительно оси не меняется, а при переходе через точки -3 и 3 — меняется.
Ответ: 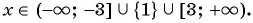
Пример №8
Решите неравенство:
а) 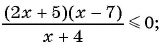
б) 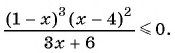
Решение:
а) Нулями функции 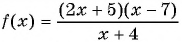 являются числа -2,5 и 7. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -4. Отметим его пустой точкой. Построим схему графика функции.
являются числа -2,5 и 7. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -4. Отметим его пустой точкой. Построим схему графика функции.
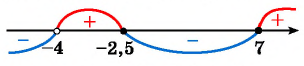
Ответ: 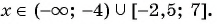
б) Умножим обе части неравенства на 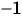 и получим неравенство
и получим неравенство 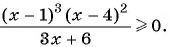 Нулями функции
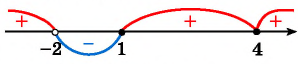
Нулями функции 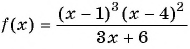 являются числа 1 и 4. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -2. Отметим его пустой точкой. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется.
являются числа 1 и 4. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -2. Отметим его пустой точкой. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется.
Ответ: 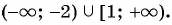
Пример №9
Решите неравенство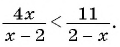
Решение:
Запишем неравенство в виде:
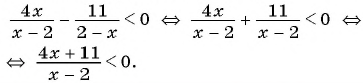
Нулем функции 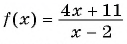 является число -2,75. Так как знак неравенства строгий, то отметим его на оси абсцисс пустой точкой. Нулем знаменателя является число 2. Отметим его на оси абсцисс пустой точкой. Построим схему графика функции.
является число -2,75. Так как знак неравенства строгий, то отметим его на оси абсцисс пустой точкой. Нулем знаменателя является число 2. Отметим его на оси абсцисс пустой точкой. Построим схему графика функции.
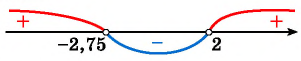
Ответ: 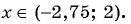
Пример №10
Решите неравенство
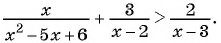
Решение:
Приведем неравенство к виду:
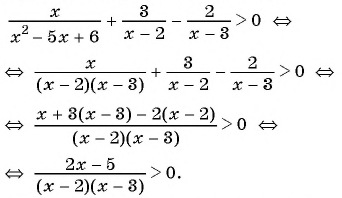
Отметим на оси абсцисс нуль функции
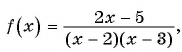 т. е.
т. е. 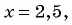 и те значения переменной, при которых значения функции не существуют: х = 2 и х = 3. Построим схему графика функции.
и те значения переменной, при которых значения функции не существуют: х = 2 и х = 3. Построим схему графика функции.
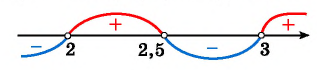
Ответ: 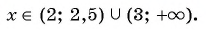
Пример №11
Найдите область определения функции 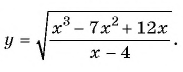
Решение:
Так как функция 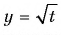 определена для
определена для 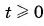 , то решим неравенство
, то решим неравенство 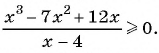 Данное неравенство равносильно неравенству
Данное неравенство равносильно неравенству 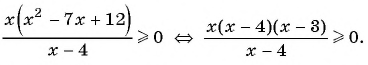
Для нахождения нулей функции 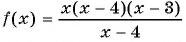 используем условие равенства дроби нулю:
используем условие равенства дроби нулю:
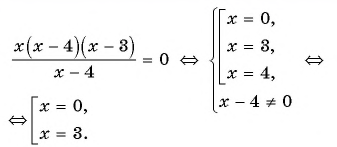
При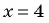 значение функции не существует. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется, так как множитель
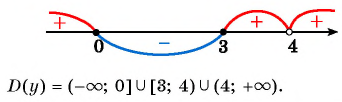
значение функции не существует. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется, так как множитель 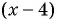 входит и в числитель, и в знаменатель, а при переходе через точки 0 и 3 положение графика меняется.
входит и в числитель, и в знаменатель, а при переходе через точки 0 и 3 положение графика меняется.
Пример №12
Решите систему неравенств
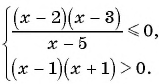
Решение:
Отметим на оси абсцисс множество решений первого неравенства системы.
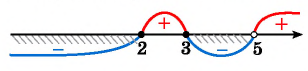 Отметим на этой же оси множество решений второго неравенства системы.
Отметим на этой же оси множество решений второго неравенства системы.
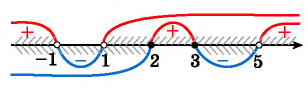 Найдем пересечение множеств решений.
Найдем пересечение множеств решений.
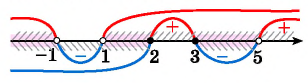
Ответ: 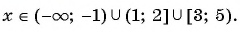
Пример №13
Найдите решение совокупности неравенств
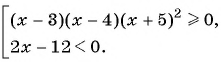
Решение:
Отметим на оси абсцисс множество решений первого неравенства совокупности.
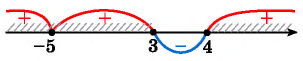
Отметим на этой же оси множество решений второго неравенства совокупности.
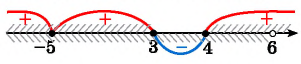
Найдем объединение множеств решений.
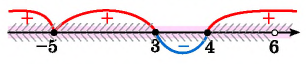
Ответ: 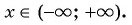
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Прогрессии в математике - арифметическая, геометрическая
- Единичная окружность - в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения