Доверительный интервал для вероятности события - определение и вычисление с примерами решения

Доверительный интервал для вероятности события:

Пусть вероятность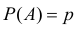

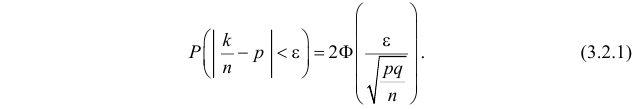
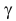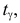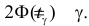По заданному уровню надежности из таблицы функции Лапласа (см. прил., табл. П2) можно найти такое  что Правая часть равенства (3.2.1) будет равна 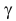, если 

откуда 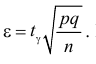При подстановке такого 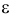в (3.2.1) получается равенство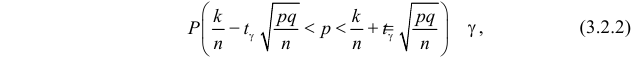 

К сожалению, в формуле (3.2.2) доверительные границы для вероятности 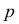выражаются через саму эту неизвестную вероятность. Это затруднение можно обойти, заметив, что 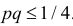Тогда формулу (3.2.2) можно записать в виде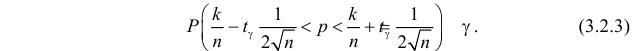 

Оценка 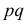 величиной 1/4 приемлема, если есть уверенность, что неизвестная вероятность 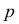близка к 1/2. Но при значениях p близких к 0 или 1 такая оценка слишком груба. Например, при 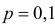получаем всего лишь 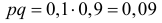вместо 0,25. Можно точный доверительный интервал заменить приближенным, если учесть, что при большом числе опытов 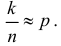Тогда из (3.2.2) следует, что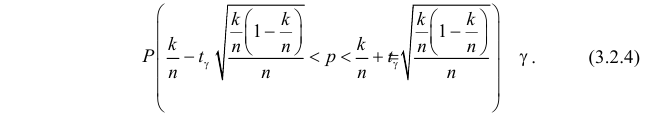 

Пример:

Для обследования большой партии изделий (несколько тысяч штук) наугад выбрано 160 изделий. Среди них оказалось 56 изделий низкого сорта. Оценить долю изделий низкого сорта в этой партии с надежностью 0,95.

Решение. Так как партия изделий крупная, то для упрощения можно считать, что по мере выбора изделий состав партии заметно не изменяется и вероятность выбрать наугад изделие низкого сорта равна доле низкосортных изделий в этой партии. Тогда задача сводится к построению доверительного интервала для вероятности выбрать из этой партии изделие низкого сорта. Частота изделий низкого сорта в выборке равна 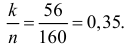 Из таблицы функции Лапласа (см. прил., табл. П2) следует, что 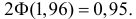Поэтому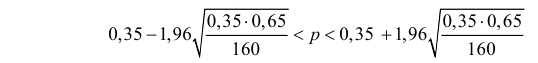
или 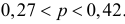  Итак, по данной выборке можно с вероятностью 0,95 утверждать, что во всей партии содержится от 27% до 42% изделий низкого сорта.

Ответ. От 27% до 42%.

Пример:

Было проведено 400 испытаний механизма катапультирования. В этих испытания не зарегистрировано ни одного отказа. С надежностью 0,95 оценить вероятность отказа механизма катапультирования.

Решение. В данной серии испытаний частота появления отказа 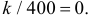Поэтому непосредственно использовать формулу (3.2.4) нельзя. Заметим, что 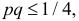так как 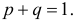Функция Лапласа 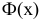строго возрастает. Поэтому меньшему значению аргумента соответствует меньшее значение функции. В расчете на худший вариант можно воспользоваться формулой (3.2.3). По таблице функции Лапласа (см. прил., табл. П2) находим, что 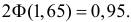Поэтому 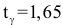и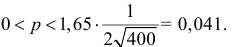

Еще раз подчеркнем, что доверительный интервал (3.2.3) построен в расчете на худший вариант, когда вероятность события близка к 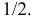Но большое число опытов  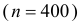и нулевая частота события в них позволяют с уверенностью утверждать, что вероятность события близка к нулю. Если несколько ухудшить статистику испытаний и посчитать что один отказ все-таки наблюдался, то 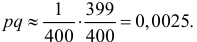Тогда по формуле (3.2.4) получаем приближенный доверительный интервал

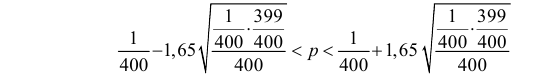
или 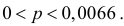 Это приближенный доверительный интервал, но он определенно более точен, чем грубая оценка по формуле (3.2.3).

Ответ.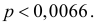

Пример:

При штамповке 70% деталей выходит первым сортом, 20% – вторым и 10% – третьим. Определить, сколько нужно взять деталей, чтобы с вероятностью равной 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортной детали не более чем на 0,05 в ту или другую сторону? Ответить на тот же вопрос, если процент первосортных деталей неизвестен.

Решение. Изготовление каждой детали можно считать независимым испытанием с вероятностью «успеха» 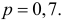 Нужно выбрать такое число испытаний 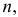чтобы по формуле (3.2.1):

По таблице функции Лапласа (см. прил., табл. П2) находим, что 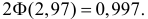Тогда 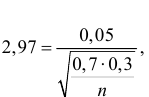откуда 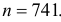Если процент первосортных деталей неизвестен, то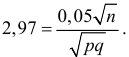

Учитывая, что 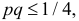и замену 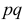на 1/4 придется компенсировать некоторым увеличением 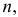получим 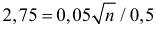или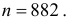

Ответ. 741; 882.

Доверительные вероятности, доверительные интервалы

В материалах сегодняшней лекции мы рассмотрим доверительные вероятности и доверительные интервалы.

При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 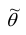параметра 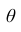, но и уметь оценить точность этой оценки. Для этого введём понятие доверительного интервала.

Доверительным интервалом для параметра 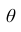называется интервал содержащий значение 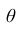с заданной вероятностью .

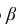Число 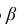называется доверительной вероятностью.

Пусть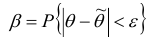 -заданное число (оно обычно равно 0,8, 0,9,
0,95,...).

Так как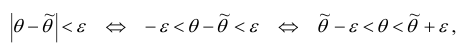 ТО
интервал 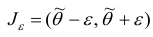содержит (накрывает) значение 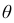(рис. 1).

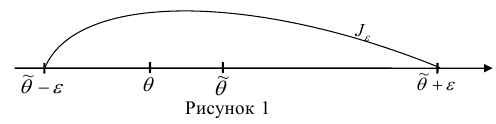
Интервал 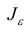- это доверительный интервал для параметра .

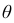Покажем, как найти доверительный интервал для математического ожидания 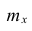с заданной доверительной вероятностью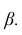

Пусть 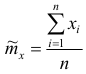   точечная оценка математического ожидания.

Используя центральную предельную теорему, можно считать, что случайная величина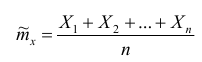 для больших п распределена по нормальному закону, а значит вероятности можно считать, используя функцию Лапласа Ф(х).

Тогда

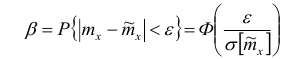
Отсюда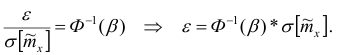

Здесь 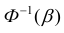находится по таблице Лапласа в обратном порядке: по
значению 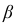 функции Ф(х) находится аргумент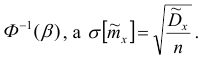

Таким образом, доверительный интервал для математического ожидании имеет вид

 

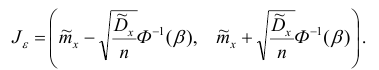
Заключение по лекции:

В лекции мы рассмотрели доверительные вероятности и доверительные интервалы.