
Доверительный интервал для математического ожидания - определение и вычисление с примерами решения
Доверительный интервал для математического ожидания:
Пусть закон распределения случайной величины Х неизвестен. Неизвестны так же 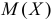
Если число наблюдений 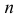 достаточно велико (хотя бы несколько десятков), то
достаточно велико (хотя бы несколько десятков), то 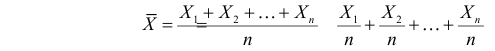
представляет из себя сумму большого числа одинаково распределенных независимых слагаемых с ограниченной дисперсией. На основании центральной предельной теоремы можно утверждать, что 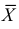 имеет близкий к нормальному закон распределения. Параметры этого нормального закона определяются тем, что
имеет близкий к нормальному закон распределения. Параметры этого нормального закона определяются тем, что 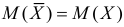 и
и 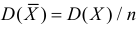 . Поэтому окончательно можно утверждать, что
. Поэтому окончательно можно утверждать, что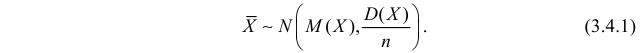
Запись формулы (2.9.3) для этого закона распределения имеет вид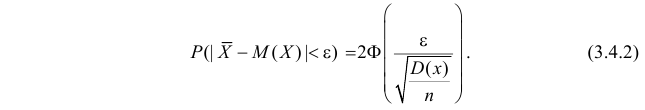
Зададим вероятность 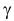 и по таблице функции Лапласа (см. прил. 1, табл. П2) выберем такое
и по таблице функции Лапласа (см. прил. 1, табл. П2) выберем такое 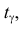 чтобы
чтобы 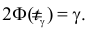 Тогда
Тогда 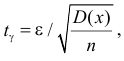 откуда
откуда 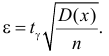 Если такое
Если такое 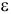 подставить в (3.4.2), то получим
подставить в (3.4.2), то получим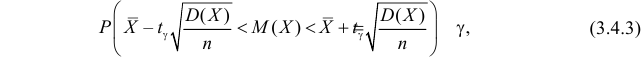
Если дисперсия случайной величины известна, то формула (3.4.3) решает задачу.
Если вместе с 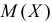 неизвестна и
неизвестна и 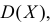 то из тех же опытных данных можно получить несмещенную и состоятельную оценку для дисперсии по формуле:
то из тех же опытных данных можно получить несмещенную и состоятельную оценку для дисперсии по формуле: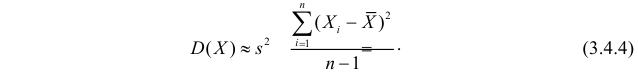
Тогда (3.4.3) имеет вид 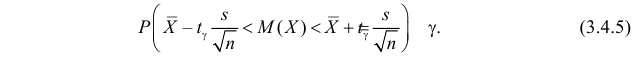
В выводе формул (3.4.3) и (3.4.5) ключевую роль играет тот факт, что при большом числе независимых наблюдений среднее арифметическое их результатов имеет близкий к нормальному закон распределения. Эту формулу можно использовать для любой случайной величины с 194 ограниченной дисперсией, лишь бы число наблюдений было достаточно велико (хотя бы несколько десятков).
Пример:
По результатам 100 наблюдений случайной величины X найдены оценки математического ожидания и дисперсии, равные 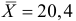 и
и 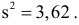 Требуется построить доверительный интервал для математического ожидания последовательно для уровней надежности
Требуется построить доверительный интервал для математического ожидания последовательно для уровней надежности 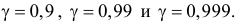
Решение. По таблице функции Лапласа (см. прил., табл. П2) находим, что 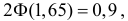 откуда
откуда 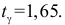 Для уровня надежности
Для уровня надежности 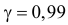 соответствующее значение
соответствующее значение 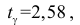 а для
а для 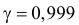 имеем
имеем 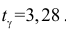 . Подставляя полученные значения в (3.4.5) можем утверждать, что
. Подставляя полученные значения в (3.4.5) можем утверждать, что 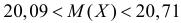 при уровне надежности
при уровне надежности 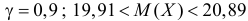 при уровне надежности
при уровне надежности 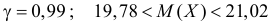 при уровне надежности
при уровне надежности 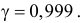
Ответ. 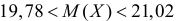 при
при 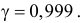
Пример:
По сгруппированным данным наблюдений случайной величины построить доверительный интервал для ее математического ожидания, соответствующий уровню надежности 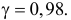

Решение. Представителем каждого интервала можно считать его середину. В данной серии из 120 наблюдений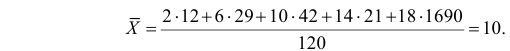
По формуле (3.1.3) оценим дисперсию случайной величины: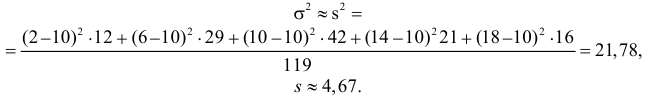
Общее число наблюдений велико. Поэтому, безотносительно к закону распределения случайной величины, можно воспользоваться формулой (3.4.3). Из таблицы функции Лапласа (см. прил., табл. П2) находим, что 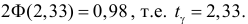 Поэтому
Поэтому 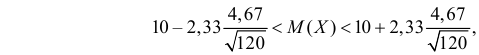
или 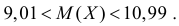
Ответ. 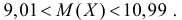
Случай малой выборки
При небольшом числе наблюдений для построения доверительного интервала необходима информация о типе закона распределения 196 случайной величины. Рассмотрим задачу в практически важном случае, когда случайная величина Х имеет нормальный закон распределения 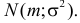
Если 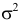 известно, а неизвестно лишь
известно, а неизвестно лишь 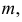 то при независимых наблюдениях можно воспользоваться свойством устойчивости нормального закона распределения. Согласно этому свойству сумма независимых случайных величин, подчиненных нормальному закону распределения, сама имеет нормальный закон распределения. Поэтому в названных условиях и при небольшом числе наблюдений можно утверждать, что
то при независимых наблюдениях можно воспользоваться свойством устойчивости нормального закона распределения. Согласно этому свойству сумма независимых случайных величин, подчиненных нормальному закону распределения, сама имеет нормальный закон распределения. Поэтому в названных условиях и при небольшом числе наблюдений можно утверждать, что 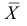 имеет нормальный закон распределения и использовать формулу (3.4.3).
имеет нормальный закон распределения и использовать формулу (3.4.3).
Если дисперсия 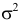 неизвестна, то при небольшом числе наблюдений ее оценка на основе опытных данных получается грубой и формула (3.4.5) не решает задачи построения доверительного интервала. В этом случае
неизвестна, то при небольшом числе наблюдений ее оценка на основе опытных данных получается грубой и формула (3.4.5) не решает задачи построения доверительного интервала. В этом случае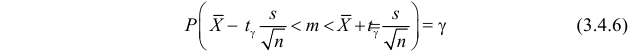
где соответствующее 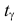 при заданном уровне надежности
при заданном уровне надежности 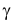 находят по таблице распределения Стьюдента (см. прил., табл. П3) для
находят по таблице распределения Стьюдента (см. прил., табл. П3) для 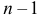 степени свободы.
степени свободы.
Формула (3.4.6) по структуре похожа на формулу (3.4.5), но 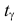 в этих формулах определяется по разным таблицам.
в этих формулах определяется по разным таблицам.
Пример:
Измерения сопротивления резистора дали следующие результаты (в омах): 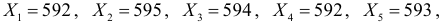
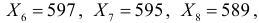
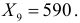 Известно, что ошибки измерения имеют нормальный закон распределения. Систематическая ошибка отсутствует. Построить доверительный интервал для истинного сопротивления резистора с надежностью 0,99 в предположении:
Известно, что ошибки измерения имеют нормальный закон распределения. Систематическая ошибка отсутствует. Построить доверительный интервал для истинного сопротивления резистора с надежностью 0,99 в предположении:
а) дисперсия ошибки измерения известна и равна четырем;
б) дисперсия ошибки измерения неизвестна.
Решение. В данной серии из девяти наблюдений 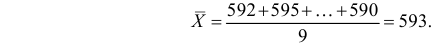
а) Если дисперсия ошибки измерения известна, то можно воспользоваться формулой (3.4.3). Для этого из таблицы функции Лапласа (см. прил., табл. П2) находим, что 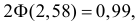 т.е. уровню надежности 0,99 соответствует значение
т.е. уровню надежности 0,99 соответствует значение 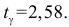 Тогда по формуле (3.4.3)
Тогда по формуле (3.4.3)
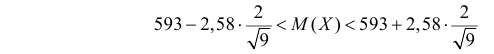
или 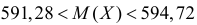 с вероятностью 0,99.
с вероятностью 0,99.
б) В случае неизвестной дисперсии ее можно оценить на основе тех же опытных данных:
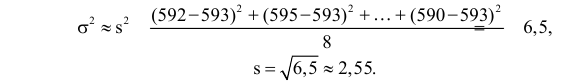
По таблице распределения Стьюдента (см. прил., табл. П3) для 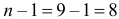 степеней свободы и заданной вероятности
степеней свободы и заданной вероятности 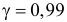 находим
находим 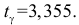 Тогда по формуле (3.4.6)
Тогда по формуле (3.4.6)
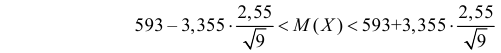
или 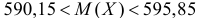 с вероятностью 0,99.
с вероятностью 0,99.
Ответ. 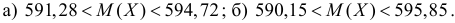
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |