
Доверительный интервал для дисперсии - определение и вычисление с примерами решения
Доверительный интервал для дисперсии:
Пусть случайная величина X имеет нормальный закон распределения 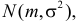
В этих условиях, согласно теореме Фишера, величина 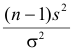 имеет распределение
имеет распределение 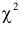 (распределение «хи-квадрат») с
(распределение «хи-квадрат») с 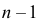 степенью свободы. Назначим уровень надежности
степенью свободы. Назначим уровень надежности 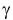 и подберем числа
и подберем числа 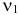 и
и 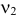 так, чтобы
так, чтобы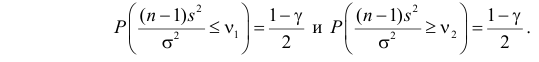
Тогда 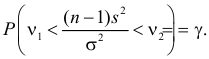
Величины 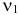 и
и 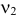 удовлетворяют равенствам
удовлетворяют равенствам 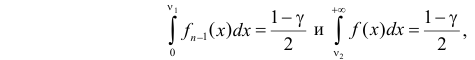
где 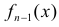 - плотность распределения «хи-квадрат» с
- плотность распределения «хи-квадрат» с 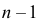 степенью свободы.
степенью свободы.
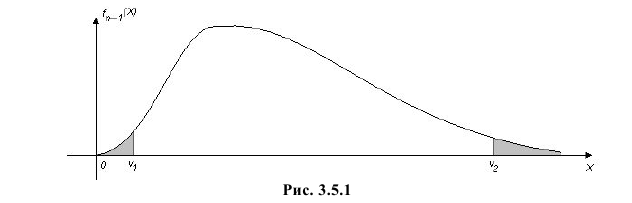
Решения этих уравнений находят с помощью таблиц (см. прил., табл. П4).
Для 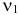 входы таблицы:
входы таблицы: 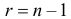 и
и 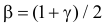 . Для
. Для 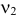 входы таблицы:
входы таблицы: 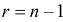 и
и 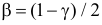 .
.
Если 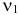 и
и 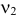 найдены, то
найдены, то 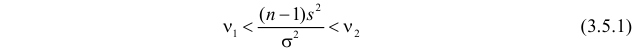
или
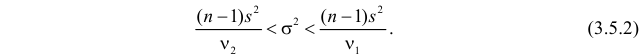
Это и есть доверительный интервал для дисперсии, соответствующий уровню надежности 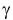 .
.
Пример:
Даны результаты наблюдений случайной величины, имеющей нормальный закон распределения с неизвестными параметрами: 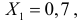
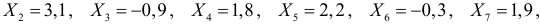
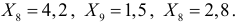 Требуется построить доверительный интервал для дисперсии при уровне надежности
Требуется построить доверительный интервал для дисперсии при уровне надежности 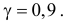
Решение. Оценим сначала математическое ожидание: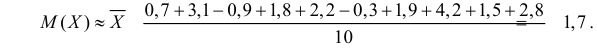
По формуле (3.1.3) оценим дисперсию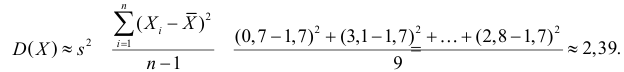
Обратимся к таблице распределения «хи-квадрат» (см. прил., табл. П4).
Для величины 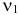 входы таблицы:
входы таблицы: 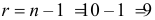 и
и 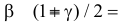
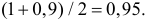 По таблице находим
По таблице находим 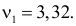 Для
Для 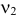 входы таблицы:
входы таблицы: 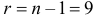 и
и 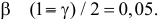 По таблице находим
По таблице находим 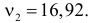
В итоге с вероятностью 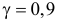 имеем, в соответствии с формулой (3.5.1),
имеем, в соответствии с формулой (3.5.1),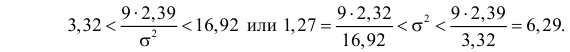
Для среднего квадратического отклонения имеем с той же надежностью 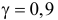 доверительный интервал
доверительный интервал 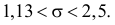
Ответ. 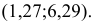
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |