
Длина дуги кривой - определение и вычисление с примерами решения
Длина дуги кривой:
Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде
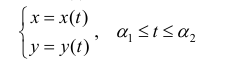
Разобьем отрезок 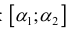
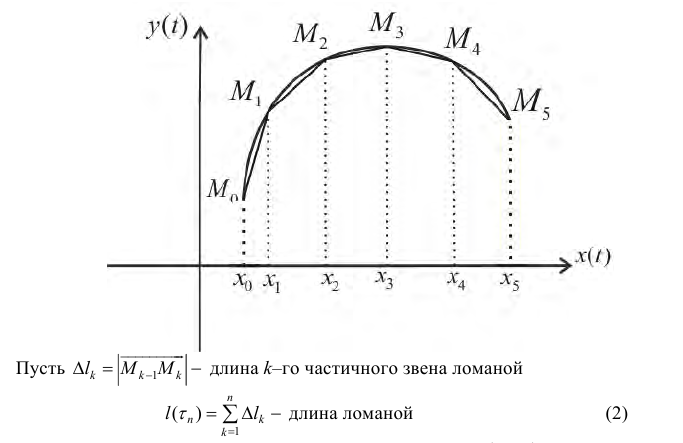
Кривая называется спрямлякмой, если множество 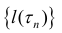 – длин всевозможных вписанных в кривую ломаных – ограничено, при этом
– длин всевозможных вписанных в кривую ломаных – ограничено, при этом 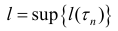 – называется длиной кривой L.
– называется длиной кривой L.
Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если 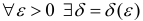 такое, что ∀ разбиения
такое, что ∀ разбиения 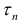 диаметром Δ < δ выполнено неравенство
диаметром Δ < δ выполнено неравенство 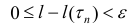 (3)
(3)
Теорема 1. Пусть x (t) и y (t) – непрерывно-дифференцируемы, тогда кривая L вида (1) – спрямляемая.
Доказательство. 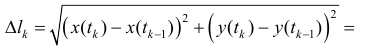 по теореме Лагранжа
по теореме Лагранжа 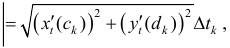 где
где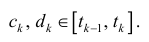
Тогда 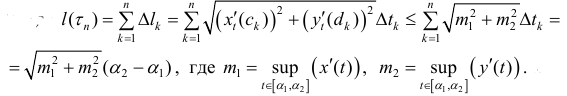
Таким образом 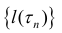 – ограничено, и следовательно имеет точную верхнюю грань, что и требовалось доказать.
– ограничено, и следовательно имеет точную верхнюю грань, что и требовалось доказать.
Найдем длину кривой L. Рассмотрим случай явного задания функции:
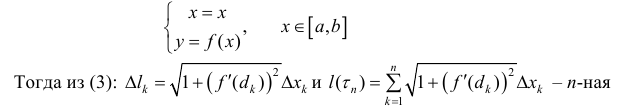
интегральная сумма для функции 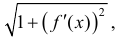 поэтому:
поэтому:
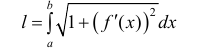 (4)
(4)
Аналогично для кривой L заданной по формулам (1)
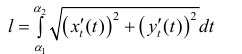 (5)
(5)
Длина l пространственной кривой L: 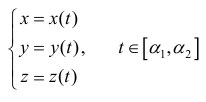 находится по формуле:
находится по формуле:
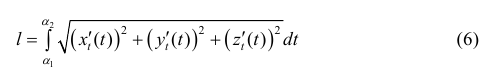
Пример 1.
Найдем длину дуги астроиды 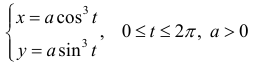
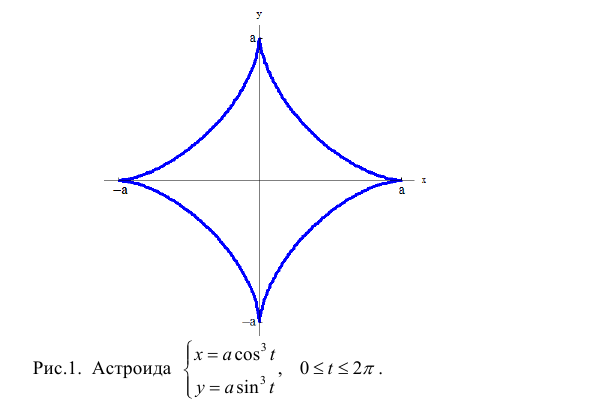
Решение.
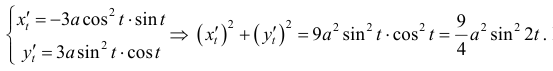
По формуле (5): 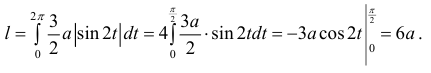
Пример 2.
Найти длину дуги линии 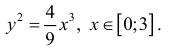
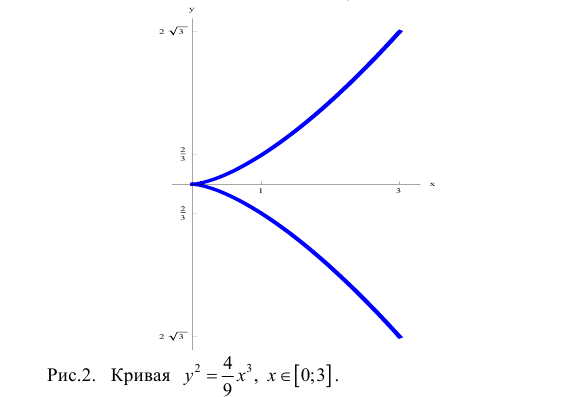
Решение.
Кривая симметрична относительно оси Ох:
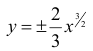 – задают верхнюю и нижнюю ветви
– задают верхнюю и нижнюю ветви 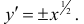 По формуле (4)
По формуле (4)
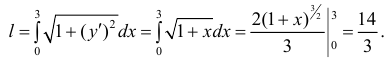 Длина всей кривой:
Длина всей кривой: 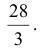
Замечание. Если кривая не является простой, необходимо учитывать возможность самоналожения участков кривой друг на друга.
Пример 3.
Найти длину кривой 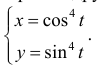
Решение.
При 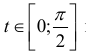 получаем график:
получаем график:
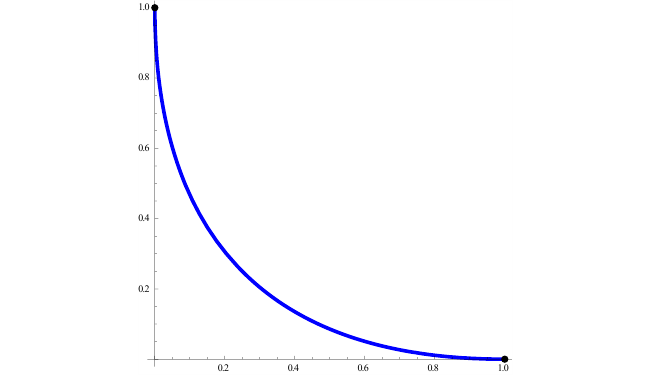
При 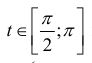 получаем тот же график, проходимый в обратном направлении (точки
получаем тот же график, проходимый в обратном направлении (точки 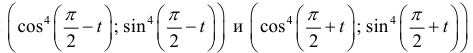 совпадают.
совпадают.
Поэтому 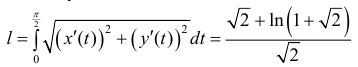 (проверить).
(проверить).
Замечание. 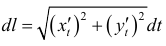 называется дифференциалом длины дуги. И тогда формула (5) перепишется в виде:
называется дифференциалом длины дуги. И тогда формула (5) перепишется в виде:
Найдем длину кривой L заданной в полярных координатах: r=r(ϕ), 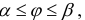 где функция r(ϕ) – непрерывно-дифференцируема. Тогда (см. формулы (1) § 31)
где функция r(ϕ) – непрерывно-дифференцируема. Тогда (см. формулы (1) § 31)
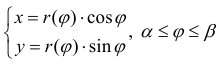 - параметрическое задание кривой;
- параметрическое задание кривой;
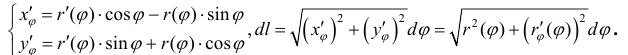
Поэтому 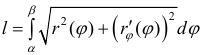 (7)
(7)
Пример 4.
Найти длину дуги части кардиоиды 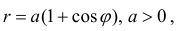 расположенной вне круга
расположенной вне круга
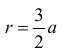 (см. пример 4 § 31).
(см. пример 4 § 31).
Решение.
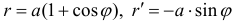
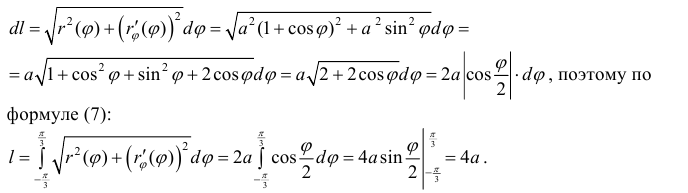
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры - виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения