Дисперсионный анализ - определение и вычисление с примерами решения

Содержание:

Сущность дисперсионного анализа:

Задачей дисперсионного анализа является изучение влияния одного или нескольких факториальных признаков на результативный признак. При этом имеется в виду, что каждый признак измерен статистически и варьирует в совокупности единиц.

Степень вариации группы единиц обычно измеряется показателями вариации: средним линейным отклонением, дисперсией, средним квадратическим отклонением и коэффициентом вариации. Определенный способ измерения и анализа вариации единиц составляет специфическую особенность дисперсионного анализа как метода изучения влияния факторов.

Применение дисперсионного анализа

При применении дисперсионного анализа требуется расчленить совокупность на группы по факториальному признаку и измерить результативный признак в каждой группе единиц. Отбор единиц в каждую группу может осуществляться методом случайной выборки (или, как ее называют в дисперсионном анализе, по принципу рэндомизации). Можно также использовать материалы проведенных ранее наблюдений. Дисперсионный анализ имеет широкое распространение в экспериментальных работах по технике и биологии. Он может быть с успехом применен и в экономических расчетах.

Дисперсия как мера вариации нам уже известна. Она представляет собой среднюю величину из квадратов отклонений всех вариантов от средней арифметической. В дисперсионном анализе принято не делить сумму квадратов отклонений на число единиц, а находить лишь сумму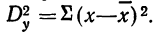

Случайная дисперсия находится как сумма квадратов отклонений всех вариантов от частных средних, т. е.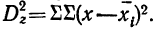

Она аналогична внутригрупповой дисперсии, рассмотренной в разделе I.

Факториальная дисперсия равна сумме квадратов отклонений частных средних от общей средней: 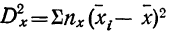 и аналогична межгрупповой дисперсии.

Дисперсия, исчисляемая как сумма квадратов отклонений, зависит от числа единиц в группе. Отношение факториальной дисперсии к дисперсии комплекса показывает долю вариации за счет фактора группировки и называется корреляционным отношением.

В дисперсионном анализе применяется и дисперсия, рассчитанная на одну степень свободы варьирования. В этом случае сумма квадратов отклонений делится на число степеней свободы.

Дисперсия на одну степень свободы в однофакторном комплексе составит:

• по комплексу
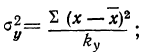
• факториальная
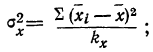
• случайная 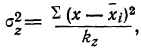 где k — число степеней свободы.

Для дисперсии комплекса число степеней свободы равно числу значений варьирующего признака без одного: 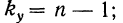для факториальной дисперсии число степеней свободы равно числу групп без одного 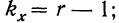для случайной дисперсии число степеней свободы равно числу значений результативного признака без числа групп 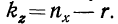Для определения достоверности влияния фактора группировки находят отношение дисперсий, исчисленных на одну степень свободы, — межгрупповой дисперсии к внутригрупповой дисперсии.

Однофакторный комплекс

Изучение методом дисперсионного анализа действия на результативный признак одного факториального признака требует расчета одного дисперсионного комплекса и называется однофакторным комплексом. Для однофакторных комплексов не требуется пропорциональности групп по их численности, так как они пропорциональны при любом соотношении частот по группам. В однофакторных комплексах вполне применимы свойства дисперсий, которые даны в разделе «Вариационные ряды и их характеристики».

Расчет однофакторного комплекса с малым числом групп может быть иллюстрирован следующим примером.

При изучении действия многих факторов заработной платы выделен один фактор — образование рабочих. Установлены 3 группы этого фактора: начальное образование, семилетнее и среднее образование. Для каждой группы было отобрано с сохранением принципа рандомизации по 3 рабочих. Заработная плата и порядок вычисления дисперсий приведен в следующей таблице:

Факториальная дисперсия 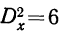и случайная дисперсия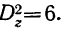
Обработаем данный однофакторный комплекс по-другому и заполним таблицу 2.

Используя свойства дисперсий и имея в виду, что в дисперсионном анализе находится не средний квадрат отклонений, а сумма квадратов отклонений, вычислим:

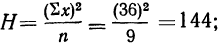
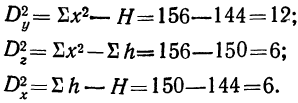
Влияние образования на вариацию заработной платы рабочих находится из корреляционного отношения:

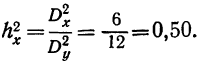
Влияние прочих факторов определится другим корреляционным отношением:

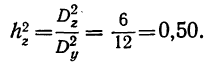
Сумма этих двух корреляционных отношений должна быть равна 1: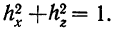

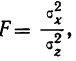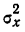Для определения достоверности влияния данного фактора определяем величину отношения дисперсий где — факториальная дисперсия, рассчитанная на одну степень свободы; 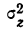—случайная дисперсия, рассчитанная на одну степень свободы.

Число степеней свободы по комплексу равно 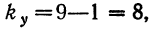для факториальной дисперсии 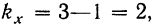для случайной дисперсии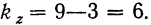

Достоверность влияния данного фактора определяется из сравнения F с некоторой стандартной величиной, исчисляемой по особой формуле, зависящей от числа степеней свободы для факториальной и случайной дисперсий. Таблица стандартных величин дана в приложении IX и определена для вероятностей 0,95 и 0,99. Если F окажется больше стандартного отношения, то вывод о наличии зависимости, основанный на дисперсионном анализе, считается обоснованным; если же F меньше любого стандартного значения, то вывод является необоснованным.

В данном примере дисперсии на одну степень свободы составят:

• факториальная
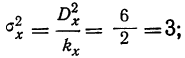
• случайная

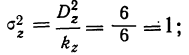
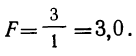
Определив величину F по эмпирическим данным, найдем по таблице стандартных отношений дисперсий стандартное F, зная, что число степеней свободы по фактору 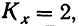 а по случайным факторам 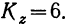(Величину стандартного F находим интерполированием, так как в приложении даны нечетные числа степеней свободы.)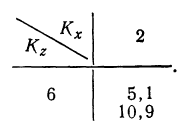

Следовательно, величина F меньше любого из стандартных отношений и вывод о значительном влиянии фактора образования нельзя считать обоснованным.

Для групп, имеющих большое число единиц, расчет дисперсионного однофакторного комплекса производится по корреляционной таблице.

Корреляционная таблица составляется по правилам, применяющимся при расчетах коэффициента корреляции и корреляционного уравнения. Однако обработка корреляционной решетки проводится особым способом, специфичным для дисперсионного анализа. Для этого к корреляционной таблице приписывается четыре строки и три столбца.

В первой приписанной строке, как и в любой корреляционной таблице, записываются суммы по столбцам, во второй строке— суммы произведений частот на отклонения 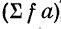, в третьей — квадраты этих сумм, в четвертой — результат деления третьей строки на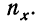

В первом приписанном столбце записываются суммы частот. Во втором и третьем столбцах находятся суммы накопленных частот. Все эти расчеты приведены в следующей таблице, где рассматривается зависимость объема ампул (у) от их диаметра (k). Вместо абсолютных величин у взяты отклонения:

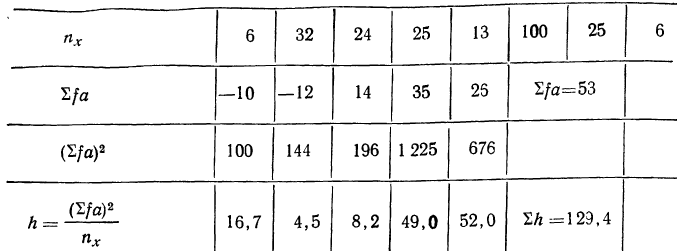
  Рассчитываем характеристики:

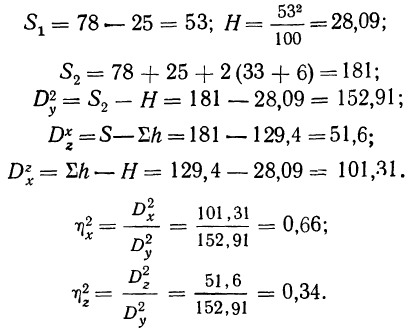
По величине корреляционного отношения 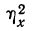 делаем вывод о том, что влияние фактора х оказывается сильным. Для определения достоверности вывода находим число степеней свободы для факториальной дисперсии 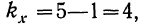случайной дисперсии 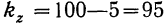и исчисляем дисперсии на одну степень

свободы: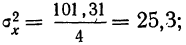

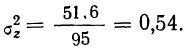
Затем вычисляем отношение: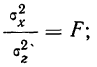 

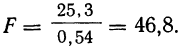
В таблице стандартных значений F при данных числах свободы 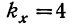и 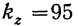 эти величины значительно меньше вычисленных на основе опытных данных. Следовательно, влияние фактора х достоверно. Вывод о существенном влиянии диаметра на объем ампул может с уверенностью считаться подтвердившимся.

Двухфакторный комплекс

При анализе влияния двух факторов на результативный признак решается двухфакторный комплекс. Решение двухфакторного комплекса отличается от решения однофакторного комплекса. При этом имеется в виду, что факторы независимы друг от друга.

Решение двухфакторного комплекса облегчается при пропорциональной численности единиц в группах.

Если изучается действие двух факторов А и В на результативный признак, то каждый фактор делится на группы по фактору А, которые в свою очередь делятся на подгруппы по фактору В.

Фактором А, например, является количество внесенных удобрений в почву, а фактором В — глубина вспашки. Оба фактора влияют на результативный признак — урожайность. Пусть даныг две группы фактора А, каждая из которых разбивается на подгруппы по фактору В. Результат группировки дан в таблице.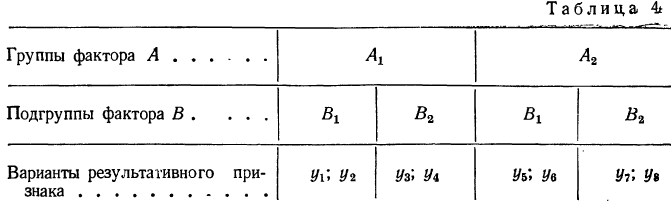

Каждый результативный признак имеет два значения. Следовательно, для каждой подгруппы было отобрано по 2 единицы изучаемой совокупности.

Анализ двухфакторного комплекса ответит на два вопроса:

1. каково суммарное действие обоих факторов;
2. как велико значение каждого фактора в отдельности и какова роль сочетания факторов.

Проще всего в этом случае предположить, что действует один фактор, распадающийся по сочетанию признаков на 4 группы (общее число подгрупп).

Тогда расчет будет вестись по схеме однофакторного комплекса. Для этого вычислим:

1. общую дисперсию
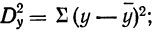
2. факториальную дисперсию
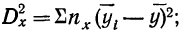
3. случайную дисперсию
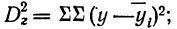
4. степень влияния объединенных факторов А и В: 
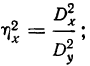
5. определим достоверность влияния объединенных факторов, для чего вычислим:

• дисперсию на одну степень свободы  
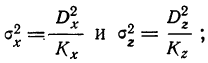
• отношение
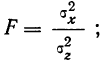
• сравним полученное отношение дисперсий F со стандартными их величинами и сделаем вывод о достоверности суммарного действия двух факторов по следующему правилу: если F фактическое больше F стандартного, то существование зависимости достоверно; если оно меньше, то оно недостоверно.

Однако еще не выяснено действие каждого из факторов и различие их совместного действия в разных комбинациях групп и подгрупп. Для этого решается двухфакторный комплекс, где сначала находятся общая и случайная дисперсии и дисперсии суммарного действия (как и в однофакторном комплексе), а затем частные факториальные дисперсии.

Частные факториальные дисперсии находятся так. Дисперсия по фактору А измеряется вариацией частных средних по
группам фактора A 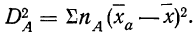В приведенном примере фактор А разделен на 2 группы. В каждой группе имеется четыре варианта. Средняя по группе 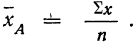Дисперсия этой средней равна сумме квадратов отклонений от общей средней.

Запишем расчет дисперсии по фактору А в табл. 5.

Аналогично вычисляются дисперсии по фактору В. Дисперсия по сочетаниям признаков 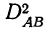находится из табл. 6, а также из формулы суммы трех частных дисперсий:

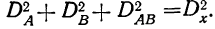
Способы определения 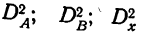описаны выше. Остается неизвестной величина 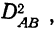которая и определяется. Но находить дисперсию по сочетаниям признаков можно только для пропорциональных комплексов.

Для определения дисперсии 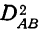можно использовать также следующую таблицу.

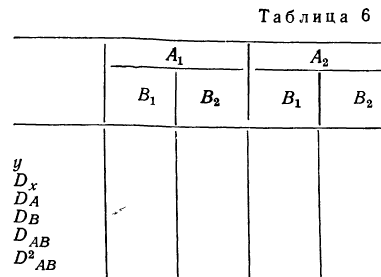
Здесь D является первой степенью отклонений. 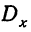— отклонения средних по подгруппам от общей средней; 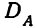— отклонения средних по группам 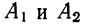от общей средней; 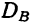— отклонения средних по группам 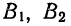от общей средней; 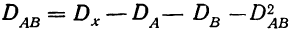и есть дисперсия по сочетанию признаков.

Разберем изложенное на конкретном примере. Методом дисперсионного анализа изучается влияние внесенных удобрений (факторов А) и глубины вспашки (факторов В) на урожай (у) (см. табл. 7). По фактору А взяты 2 группы участков: хорошо удобренные и мало удобренные.

По фактору В также 2 группы: с глубокой вспашкой и с мелкой. В каждую группу отобрали методом рэндомизации (случайной выборки) по 2 участка, которые имели следующую урожайность (у): 14; 16; 12; 10; 8; 10; 4; 6.

Общая дисперсия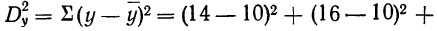  

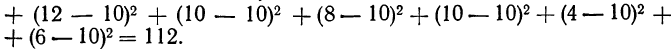
Факториальная дисперсия суммарного действия факторов определяется по формуле: 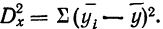 Для вычисления необходимо прежде всего найти частные средние по подгруппам: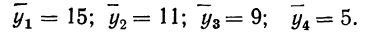

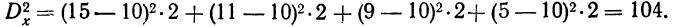
Случайная дисперсия выразится: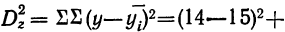

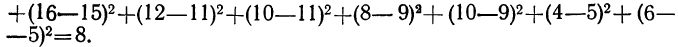
Вычислим частную факториальную дисперсию по фактору А.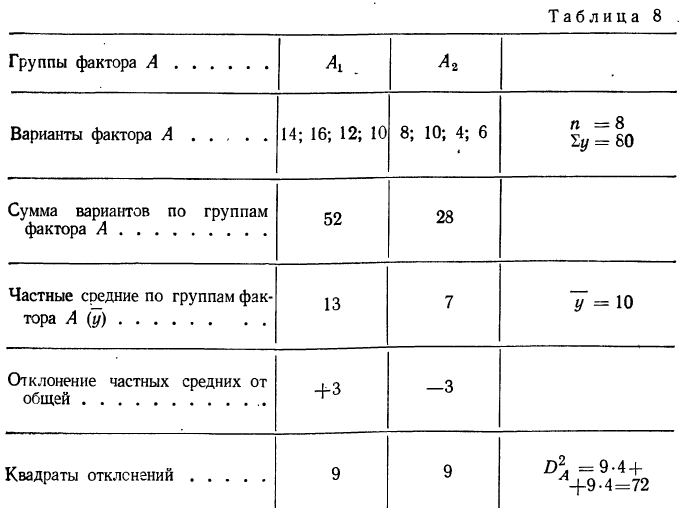

Отношение 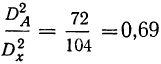говорит о том, что удельный вес влияния фактора А составляет 69% суммарного действия факторов А и В.
Отношение 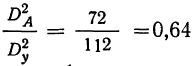  говорит о том, что удельный вес влияния фактора А составляет 59% действия всех факторов. Рассчитаем частную факториальную дисперсию по фактору В в табл. 9.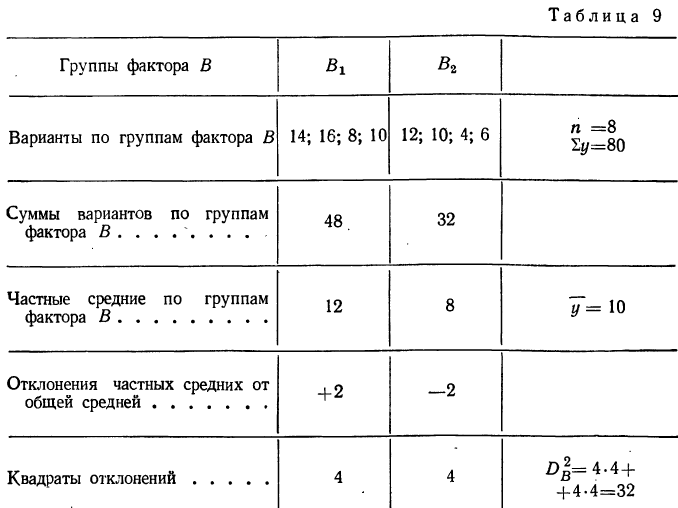

Влияние фактора В в суммарном влиянии факторов А и В составит 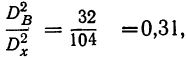 или 31%. Влияние фактора В в общем влиянии всех факторов составляет  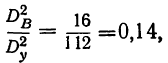или 14 %.

Вычислим дисперсию по сочетанию факторов АВ, т. е. дисперсию 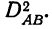 Для этого составим табл. 10. Влияние сочетания факторов равно нулю. Это означает, что в данном комплексе действие одного фактора не зависит от действия другого.

Находим число степеней свободы и определяем дисперсии на одну степень свободы для рассмотрения достоверности влияния факторов.

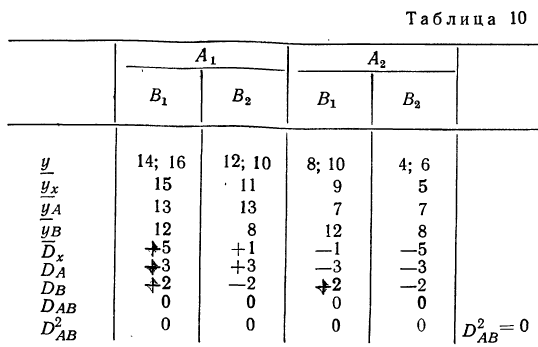
Для общей дисперсии число степеней свободы равно: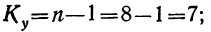

• для факториальных дисперсий по факторам А и В число степеней свободы равно числу групп без одного
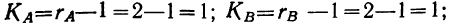
• для дисперсии сочетания факторов число степеней свободы 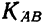равно произведению 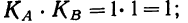для суммарной дисперсии число степеней свободы равно произведению числа групп по обоим факторам без одного;

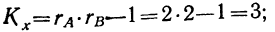
для случайной дисперсии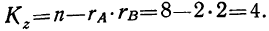 

Проверяем, чтобы

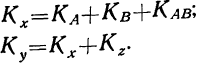
В нашем примере:

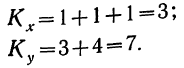
Дисперсии на одну степень свободы составят.

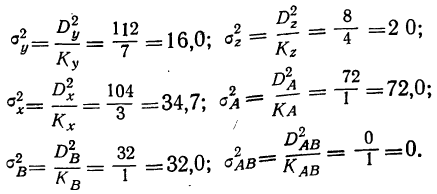
Определим величину F для каждой дисперсии. Для этого делим каждую факториальную дисперсию на случайную.

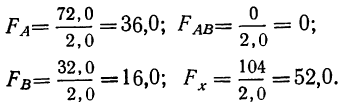
Сравниваем каждое отношение дисперсий F со стандартными величинами, данными в таблице, учитывая число степеней свободы обеих взятых дисперсий.

Для фактора A 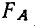превышает стандартное отношение. Следовательно, влияние фактора А можно считать достоверным. Для фактора В 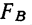превышает второе стандартное отношение. Влияние фактора В достоверно. Для сочетания факторов А и В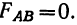 

Для суммарного действия факторов сравниваем 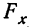со стандартным отношением при данных числах степеней свободы. Оно превышает любую стандартную величину. Значит, суммарное действие обоих факторов весьма достоверно.

Используя свойства дисперсии, можно составить упрощенную схему расчета двухфакторного комплекса. При этом расчет общей дисперсии 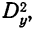случайной дисперсии 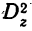и дисперсии суммарного действия обоих факторов 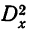производится так же, как и в однофакторном комплексе, т. е. путем нахождения вспомогательной величины Н, где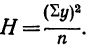

Тогда

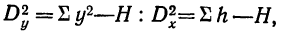
где 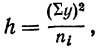т. е. исчисляется по той же формуле, что и Н, но только 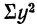берется по подгруппам.

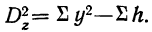
Дисперсии по факторам А и В, а также дисперсию по сочетанию факторов АВ находим по тем же формулам. Так, дисперсия по фактору A 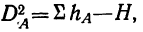а дисперсия по фактору В 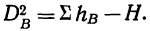Дисперсию по сочетанию факторов найдем из дисперсии суммарного действия  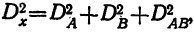откуда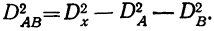 

Вычислим дисперсии по факторам А и В для приведенного выше примера.

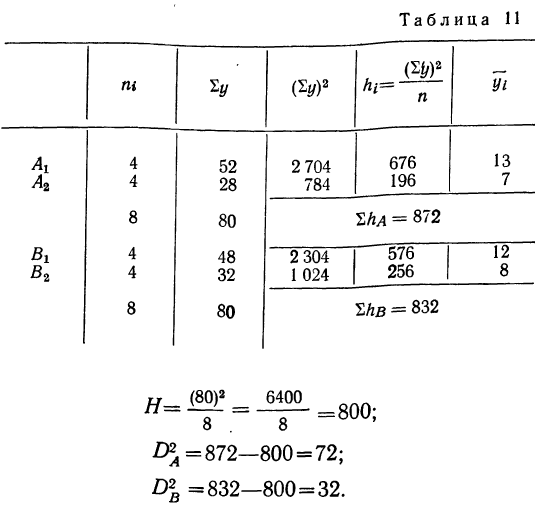
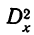найдена ранее и составляла 104.

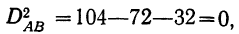что и подтверждает ранее приведенный расчет.

Расчет двухфакторного комплекса при большом числе наблюдений ведется по корреляционной таблице по той же схеме, как и для однофакторного комплекса. Дисперсии можно находить по способу сумм по формулам:

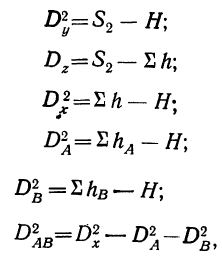
где 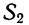— вторые накопленные суммы.

Исследование продолжаем далее по общей схеме дисперсионного анализа.

Анализ дисперсий трехфакторного комплекса ведется по тому же принципу, что и двухфакторного комплекса, только в этом случае будет 3 дисперсии по факторам 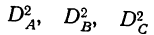 и 4 дисперсии по сочетанию признаков: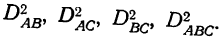

 

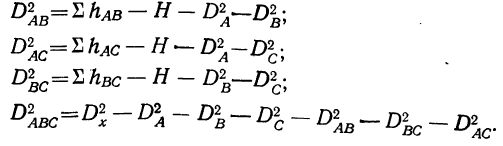
Непропорциональные комплексы

Непропорциональными называются дисперсионные комплексы, в которых не соблюдается пропорциональность численностей вариантов.

В непропорциональных дисперсионных комплексах дисперсия суммарного действия факторов не равна сумме дисперсий по факторам и дисперсии сочетания факторов. Между этими дисперсиями существует следующая связь: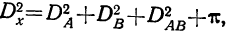

где 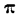— величина, зависящая от степени статистических связей, возникающих в непропорциональных комплексах между отдельными факторами вследствие нарушения пропорциональности.

Для пропорциональных комплексов 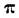 =0. Однако в непропорциональных комплексах не нарушается равенство: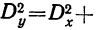 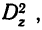так как расчет дисперсий в этом случае происходит по принципам однофакторного комплекса, а однофакторные комплексы всегда пропорциональны.

При решении непропорциональных комплексов создаются затруднения не только при отыскании дисперсий, но также при определении степени влияния каждого фактора, так как сумма частных влияний не равна суммарному влиянию. Влияние каждого фактора определяется при помощи соответствующего корреляционного отношения.

В непропорциональных комплексах общее корреляционное отношение не состоит из суммы частных корреляционных отношений, так как имеется еще слагаемое it, которое не имеет реального смысла и носит условный характер.

Чтобы определить, как влияет каждый из факторов в непропорциональном комплексе, необходимо иметь единую структуру комплекса.

Одним из способов приведения непропорционального комплекса к единой структуре является способ его замены пропорциональным комплексом, в котором частоты осереднены по группам. Когда такая замена произведена, комплекс решается по принципам пропорциональных комплексов в отношении 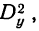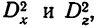но расчет 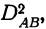т. е. дисперсии сочетаний действия , факторов, идет по-другому.

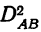определяется при помощи нахождения отклонений первой степени по схеме: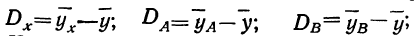 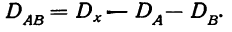Квадраты этих отклонений и дают соответствующие дисперсии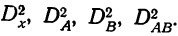

Мы не должны при этом смущаться тем обстоятельством, что сумма составляющих дисперсий 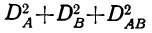 не равна суммарной дисперсии 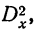найденной в общей части комплекса.

Величину дисперсии 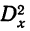разделяют пропорционально полученным величинам дисперсий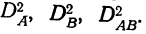

Так получается комплекс, общая часть которого совпадает с пропорциональной частью комплекса, а отношения между частными дисперсиями пропорциональны соотношениям частных дисперсий в исходном комплексе.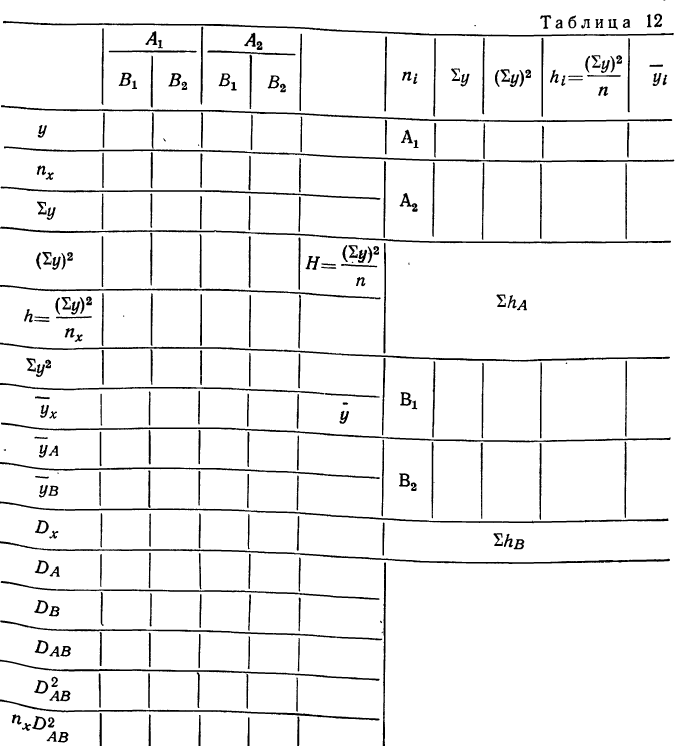

Схема расчета непропорционального комплекса дана в таблице 12.

Альтернативный комплекс

Если исследование методом дисперсионного анализа ведется по альтернативному признаку, в котором из n единиц у m единиц имеется данный признак, то расчет ведется несколько по-другому, чем в варьирующих комплексах.

Дисперсия альтернативного комплекса исчисляется по формул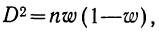е: где 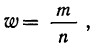откуда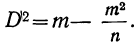
Используя свойства дисперсии приведем их к расчету по сокращенным формулам:

Расчет однофакторного альтернативного комплекса удобно вести, как показано в табл. 13, где в качестве группировочного признака выступают различные показатели одного и того же признака. Например, изучая действие режима работы (хотя бы, например, температуры) на качество продукции, мы выделяем несколько групп по этому признаку.

Определение достоверности вывода ведется исходя из соответствия эмпирического F стандартному. Число степеней свободы определяется по формулам: для общей дисперсии 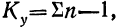для факториальной дисперсии 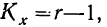для случайной дисперсии 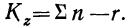Дисперсия на одну степень свободы определится отношением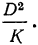

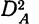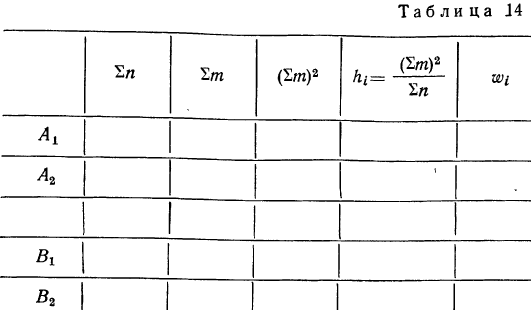
Расчет двухфакторного альтернативного комплекса ведется в общей части по тем же правилам и схемам, что и в однофакторном альтернативном комплексе. Расчет же частных дисперсий и 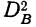лучше вести в специальной таблице типа табл. 12, в которой объединены соответствующие группы и подгруппы m и n.
               

Используя данные табл. 14, будем иметь все необходимое для расчета дисперсий 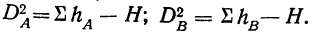Расчет же дисперсий по сочетанию факторов 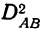производим путем вычитания из общей факториальной дисперсии частных дисперсий, т. е.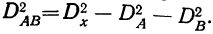

                 

Достоверность вывода определяется методами, известными из предыдущего изложения.

При помощи дисперсионного анализа сравниваются также средние величины по группам комплекса и устанавливается достоверность разности между ними. Однако изложение этих методов не входит в нашу задачу.