
Динамика в физике - основные понятия, формулы и определения с примерами
Содержание:
Динамика (от греч. - сильный, сила) - раздел механики, в котором изучается движение материальных тел под действием приложенных к ним сил.
В механике, кроме кинематического описания движений, возникает необходимость выявления причин изменения состояния движения. Для этого рассматривают механическое движение тела, учитывая действие других тел, т. е. движение под действием приложенных к нему сил. Этот раздел механики называют динамикой.
Взаимодействие тел и первый закон Ньютона
Вам уже известно, что окружающие нас тела взаимодействуют друг с другом. Каким закономерностям подчиняются взаимодействия тел? Как они влияют на механическое движение тел? Ответы на эти вопросы дает раздел физики динамика.
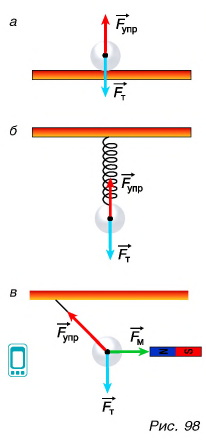
Рассмотрим взаимодействие стального шарика с различными телами (рис. 98, а, б, в). Шарик находится в состоянии покоя.
С какими телами взаимодействует шарик в случае а? С Землей и опорой.
Количественной мерой взаимодействия, как вам известно, является сила. Земля притягивает шарик силой тяжести 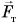
Действующие силы компенсируют друг друга 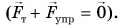 Шарик находится в состоянии покоя относительно опоры.
Шарик находится в состоянии покоя относительно опоры.
В случае б сила упругости действует на шарик со стороны растянутой пружины. В обоих случаях шарик взаимодействовал с двумя телами: Землей и опорой (рис. 98, а), с Землей и пружиной (рис. 98, б). Значит, число сил, приложенных к телу, равно числу тел, с которыми данное тело взаимодействует.
В земных условиях любое тело взаимодействует хотя бы с одним телом (Землей).
В случае в на шарик действуют три тела: Земля с силой 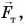 нить с силой
нить с силой 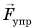 и магнит с силой
и магнит с силой 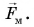 Сумма всех сил, приложенных к шарику, как и в случаях а и б, равна нулю:
Сумма всех сил, приложенных к шарику, как и в случаях а и б, равна нулю: 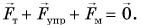 Шарик находится в состоянии покоя относительно Земли.
Шарик находится в состоянии покоя относительно Земли.

А при каком условии шарик сохранял бы состояние равномерного прямолинейного движения? Повседневный опыт говорит: чтобы тело двигалось равномерно, его нужно тянуть или толкать (рис. 99), прилагая силу. Прекратится действие силы — движущееся тело рано или поздно остановится. Так считали и известные ученые древности, например Аристотель. Опровергнуть эти представления удалось в первой половине XVII в. итальянскому ученому Галилео Галилею.
Проведем опыт, подобный опытам Галилея. Пустим с некоторой высоты железный шарик по наклонному желобу (рис. 100). Шарик скатывается с желоба и продолжает движение по горизонтальной поверхности стола, покрытого тканью (рис. 100, а), картоном (рис. 100, б), стеклом (рис. 100, в).
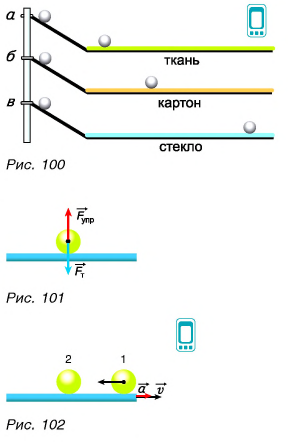
Опыт показывает, что по стеклу шарик прокатится дальше всего. Почему? Потому что в этом случае трение было наименьшим. А если бы трения не было совсем? На шарик действовали бы только две силы: сила тяжести 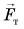 и сила упругости
и сила упругости 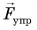 (рис. 101), компенсирующие друг друга. Шарик двигался бы с постоянной скоростью как угодно долго.
(рис. 101), компенсирующие друг друга. Шарик двигался бы с постоянной скоростью как угодно долго.
Галилей сделал вывод: скорость движения тела остается постоянной, если на тело не действуют силы или силы действуют, но при этом компенсируют друг друга. Такое движение называют движением но инерции.
Развивая идеи Галилея, в 1687 г. Исаак Ньютон сформулировал утверждение, получившее название первый закон Ньютона (или за кон инерции): всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока на него не подействуют силы.
В первом законе Ньютона заключена важнейшая идея механики. Действовать на тело силой необходимо не для того, чтобы сохранить его скорость постоянной, а для того, чтобы изменить ее. Сила нужна как для изменения модуля скорости, так и для изменения ее направления.
Мы знаем, что скорость тела зависит от системы отсчета. В любой ли системе отсчета выполняется первый закон Ньютона?
Приведем в ускоренное движение опору, на которой покоится шарик (см. рис. 101). Относительно опоры шарик начнет двигаться ускоренно в противоположную сторону (от положения 1 к положению 2) (рис. 102). Но ведь на шарик действовали те же силы 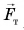 и
и 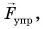 которые по-прежнему компенсировали друг друга:
которые по-прежнему компенсировали друг друга: 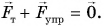
Какая же сила вызвала движение шарика? Такой силы нет. Просто первый закон Ньютона выполняется в системе отсчета, покоящейся относительно Земли, но не выполняется в системе отсчета, связанной с ускоренно движущейся опорой.
Системы отсчета, относительно которых тела покоятся или движутся равномерно и прямолинейно, когда на них не действуют силы (или силы скомпенсированы), называются инерциальными.
Значит, система отсчета, связанная с Землей, является инерциальной системой отсчета, а система отсчета, связанная с ускоренно движущейся относительно Земли опорой — неинерциальной. Существование систем отсчета, близких к инерциальным, — важнейший, проверенный экспериментально, факт. Поэтому первому закону Ньютона дают следующую формулировку: существуют системы отсчета, относительно которых любое тело движется равномерно и прямолинейно, если на него не действуют силы или действие сил скомпенсировано.
Для любознательных:
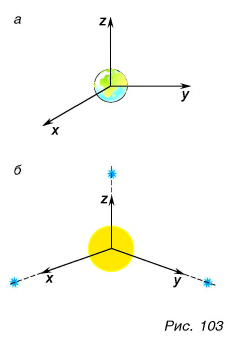
Опыты показывают, что систему отсчета, связанную с Землей, — геоцентрическую систему (рис. 103, а) — можно считать инерциальной только приближенно. Гораздо более близка к инерциальной гелиоцентрическая система отсчета. Ее начало координат связано с Солнцем, а оси координат направлены на далекие звезды (рис. 103, б).
Любая система отсчета, движущаяся относительно инерциальной системы поступательно, равномерно и прямолинейно, также будет инерциальной. Если же система отсчета движется ускоренно или вращается относительно инерциальной системы, то она будет неинерциальной. Например, неинерциальные системы отсчета — это системы, связанные с ракетой на участке разгона, с тормозящим поездом, вращающейся каруселью и т. п.
Мы не замечаем неинерциальности геоцентрической системы из-за того, что Земля вращается вокруг своей оси медленно (один оборот за 24 ч).
Главные выводы:
- Количественной мерой взаимодействия является сила.
- Если все силы, действующие на тело, скомпенсированы или их нет, то тело находится в состоянии покоя или в состоянии равномерного прямолинейного движения.
- Равномерное движение тела при действии на него скомпенсированных сил называется движением по инерции.
- Система отсчета называется инерциальной, если тела, на которые не действуют силы, покоятся или движутся относительно нее равномерно и прямолинейно.
- Первый закон Ньютона в современной формулировке: «Существуют системы отсчета, относительно которых любое тело движется равномерно и прямолинейно, если на него не действуют силы или действие сил скомпенсировано».
Масса
Мы часто вместо слова «масса» говорим «вес», а слова «массивный» и «тяжелый» считаем синонимами. С точки зрения физики это грубая ошибка.
Представим, что на космической станции, построенной на Луне, проходят соревнования по подъему штанги. На них любой из вас смог бы поднять стокилограммовую штангу! Легче ли штанга на Луне, чем на Земле? Да. Меньше ли на Луне масса штанги? Нет. Так что такое масса? Каковы ее свойства?
Как измеряют массу
1. Измерение массы тел путем взвешивания
Существуют различные типы весов:
- • рычажные (рис. 104, а, б);
- • пружинные (рис. 104, в, г);
- • электронные (рис. 104, д).
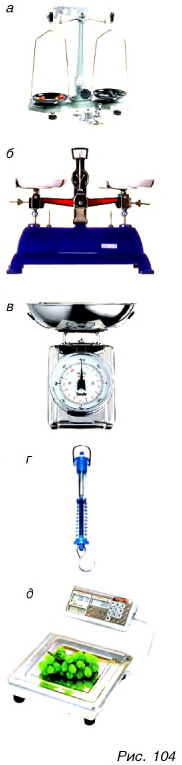
Во всех случаях весы — прибор для определения массы тела по действующей на него силе тяжести.
Как вы знаете, сила тяжести прямо пропорциональна массе тела:

Рычажные весы с равными плечами находятся в равновесии, если силы тяжести взвешиваемого тела и набора гирь будут равны: 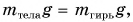 т. е. при
т. е. при 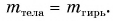 Значит, результат взвешивания тела на рычажных весах не зависит от значения коэффициента g и будет одним и тем же на Земле, Луне и любой планете.
Значит, результат взвешивания тела на рычажных весах не зависит от значения коэффициента g и будет одним и тем же на Земле, Луне и любой планете.
А как измерить массу тела на пружинных весах? Их показания пропорциональны силе тяжести. Сила тяжести на Луне примерно в 6 раз меньше, чем на Земле. Во столько же раз меньше будут и показания пружинных весов.
Чтобы правильно определить массу тела на пружинных весах, нужно провести взвешивание гири-эталона массой 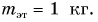 Сравнивая показания пружинных весов для тела и эталона
Сравнивая показания пружинных весов для тела и эталона 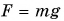 и
и 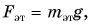 получим:
получим:

откуда

Формула (3) выражает массу тела независимо от того, где проводилось взвешивание.
А можно ли найти массу тела, не используя силу тяжести? Можно, сравнивая инертность тел.
2. Сравнение масс по инертности тел
Любое тело обладает свойством двигаться по инерции, т. е. сохранять свою скорость неизменной, если на него не действуют силы (или силы компенсируют друг друга). Однако одни тела легче разогнать (а разогнав, остановить), а другие — труднее. Например, для разгона или остановки нагруженной тележки на нее следует действовать гораздо большей силой, чем па порожнюю. Груженая тележка более инертна.
Как определить, во сколько раз одно тело более инертно, чем другое?
Проведем опыт. Поставим на горизонтальную поверхность две легкие тележки, нагруженные телами 1 и 2 соответственно (рис. 105), способные катиться почти без трения.
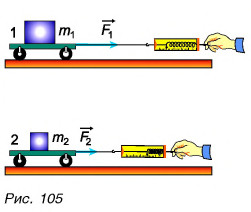
Будем разгонять тележки так, чтобы они двигались с одинаковым ускорением, не обгоняя и не отставая друг от друга. Пусть для этого на тележку 1 пришлось подействовать силой 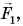 в три раза большей, чем сила
в три раза большей, чем сила 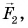 приложенная к тележке 2.
приложенная к тележке 2.
Значит, тело 1 в три раза инертнее тела 2. Или, другими словами, масса как мера инертности у тела 1 в три раза больше, чем у тела 2.
Современные, очень точные опыты показывают, что сравнение масс тел путем взвешивания и путем сравнения их инертности дают одинаковые результаты.
Напомним еще о двух практически важных свойствах массы:
• общая масса 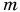 нескольких тел равна сумме их масс:
нескольких тел равна сумме их масс:

• масса однородного тела объемом 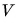 равна:
равна:

где 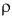 — плотность вещества, из которого состоит тело.
— плотность вещества, из которого состоит тело.
Для любознательных:
Массу как меру инертности называют инертной массой, а массу, определяемую по силе притяжения тел друг к другу, — гравитационной массой.
Равенство инертной и гравитационной масс неоднократно проверялось на опыте.
Главные выводы:
- Масса тела — мера его инертности.
- Масса тела — мера его гравитационных свойств.
- Масса данного тела на Земле, на Луне, на космической станции и т. д. одинакова.
Второй закон Ньютона — основной закон динамики
Первый закон Ньютона отвечает на вопрос: «Как ведет себя тело, если на него действуют силы, которые компенсируют друг друга?» А что будет с телом, если силы не скомпенсированы? На этот вопрос дает ответ второй закон Ньютона.
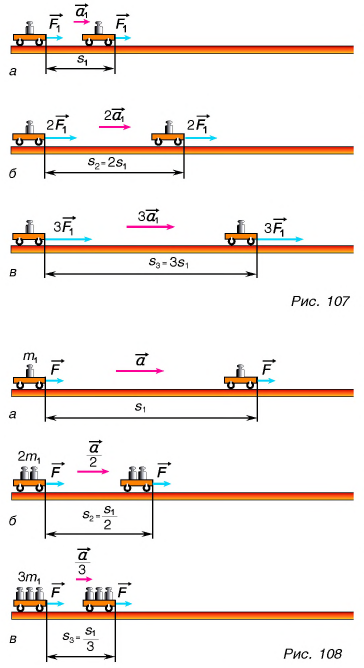
Рассмотрим опыт. Приложим силу 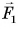 к тележке, находящейся на гладкой горизонтальной поверхности (рис. 107, а). Кроме силы
к тележке, находящейся на гладкой горизонтальной поверхности (рис. 107, а). Кроме силы 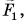 на тележку действуют сила тяжести и реакция опоры (на рисунке они не показаны), которые компенсируют друг друга. Силой трения качения можно пренебречь. Поэтому сила
на тележку действуют сила тяжести и реакция опоры (на рисунке они не показаны), которые компенсируют друг друга. Силой трения качения можно пренебречь. Поэтому сила 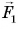 равна результирующей всех сил, приложенных к тележке. Под действием силы
равна результирующей всех сил, приложенных к тележке. Под действием силы 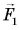 тележка приобретает ускорение
тележка приобретает ускорение 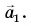
Ускорение тележки будем определять по формуле 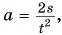 пройденный путь s измерять рулеткой, время t — секундомером, силу F — динамометром. Как связано ускорение с приложенной к тележке результирующей силой?
пройденный путь s измерять рулеткой, время t — секундомером, силу F — динамометром. Как связано ускорение с приложенной к тележке результирующей силой?
Увеличим силу в два раза 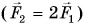 (рис. 107, б). За такое же время t тележка пройдет путь, в 2 раза больший:
(рис. 107, б). За такое же время t тележка пройдет путь, в 2 раза больший: 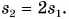 Значит,
Значит, 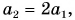 т. е. в два раза большая сила сообщает телу в два раза большее ускорение. Продолжив опыты, получим, что при увеличении результирующей силы в
т. е. в два раза большая сила сообщает телу в два раза большее ускорение. Продолжив опыты, получим, что при увеличении результирующей силы в 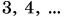 раза модуль ускорения а увеличится тоже в
раза модуль ускорения а увеличится тоже в 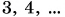 раза. Сделаем вывод.
раза. Сделаем вывод.
Ускорение тела прямо пропорционально результирующей всех сил, приложенных к нему:

А как зависит ускорение от массы тела? Будем теперь силу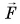 прикладывать к телам разных масс (рис. 108, а, б, в). Под действием одной и той же силы тело в 2 раза большей массы приобретет в 2 раза меньшее ускорение. Ускоряя тела в
прикладывать к телам разных масс (рис. 108, а, б, в). Под действием одной и той же силы тело в 2 раза большей массы приобретет в 2 раза меньшее ускорение. Ускоряя тела в 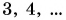 раза большей массы, мы увидим, что модуль ускорения в
раза большей массы, мы увидим, что модуль ускорения в 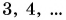 раза уменьшится.
раза уменьшится.
Модули ускорений, приобретаемых телами под действием одинаковых сил, обратно пропорциональны массам этих тел:

А как направлено ускорение? В нашем опыте направления ускорения 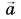 и силы
и силы 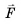 совпадали (рис. 108). Рассмотрим еще два примера.
совпадали (рис. 108). Рассмотрим еще два примера.
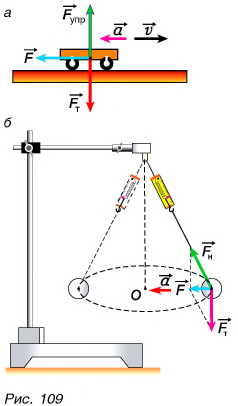
- К тележке приложили силу
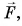 направленную против ее скорости
направленную против ее скорости 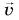 (рис. 109, а). Скорость тележки будет уменьшаться, и ее ускорение
(рис. 109, а). Скорость тележки будет уменьшаться, и ее ускорение 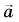 будет направлено противоположно скорости, но так же, как и результирующая сила
будет направлено противоположно скорости, но так же, как и результирующая сила 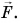
- Шарик, подвешенный на нити, движется по окружности (рис. 109, б). Ускорение шарика направлено к ее центру О. Опыт показывает, что и в этом случае направления ускорения
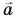 и результирующей
и результирующей 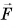 всех сил, приложенных к телу (силы тяжести
всех сил, приложенных к телу (силы тяжести 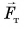 и силы натяжения нити
и силы натяжения нити 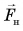 ), совпадают.
), совпадают.
В итоге приходим к выводу.
Ускорение тела прямо пропорционально результирующей всех сил, приложенных к нему, обратно пропорционально массе тела и направлено так же, как результирующая сила:

Это основной закон динамики — второй закон Ньютона. Из формулы (3) следует, что направления ускорения 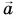 и результирующей силы
и результирующей силы 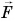 совпадают.
совпадают.
Запишем второй закон Ньютона в виде:

В соответствии с формулой (4) определяется единица силы в СИ — ньютон (Н).
1 Н — сила, под действием которой тело массой 1 кг приобретает ускорение 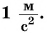
В каких системах отсчета выполняется второй закон Ньютона? В § 15 мы выяснили, что если система неинерциальна, то при результирующей 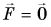 ускорение тела
ускорение тела 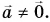 Но согласно второму закону Ньютона при
Но согласно второму закону Ньютона при 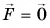 ускорение
ускорение 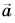 должно быть равно нулю. Значит, второй закон Ньютона выполняется только в инерциальных системах отсчета.
должно быть равно нулю. Значит, второй закон Ньютона выполняется только в инерциальных системах отсчета.
А как применять формулу (4), если тело нельзя рассматривать как материальную точку? В таких случаях под ускорением 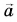 следует понимать ускорение точки, называемой центром тяжести этого тела. Понятие «центр тяжести» мы рассмотрим в следующем разделе.
следует понимать ускорение точки, называемой центром тяжести этого тела. Понятие «центр тяжести» мы рассмотрим в следующем разделе.
Главные выводы:
- Ускорение тела прямо пропорционально результирующей всех сил, действующих на него, и обратно пропорционально массе тела.
- Ускорение тела направлено так же, как результирующая всех приложенных к нему сил.
- Единица силы в СИ — 1 ньютон. Это сила, под действием которой тело массой 1 кг движется с ускорением
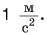
- Второй закон Ньютона выполняется только в инерциальных системах отсчета.
Пример №1
Сани массой 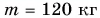 тянут по горизонтальному участку пути, прикладывая силу
тянут по горизонтальному участку пути, прикладывая силу 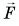 под углом
под углом 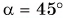 к горизонту. Модуль силы
к горизонту. Модуль силы 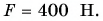 Модуль силы трения скольжения
Модуль силы трения скольжения 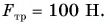 Определите ускорение саней. Примите
Определите ускорение саней. Примите 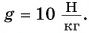
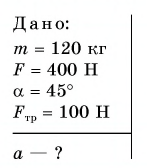
Решение
Сделаем рисунок к задаче (рис. 110).
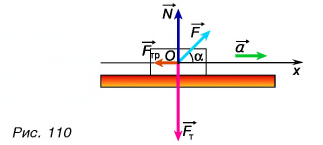
К саням приложены четыре силы: сила тяжести 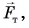 сила реакции опоры
сила реакции опоры 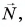 сила трения
сила трения 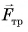 и сила
и сила 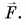 По второму закону Ньютона:
По второму закону Ньютона:
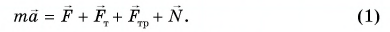
В проекции на ось Ох уравнение (1) примет вид:
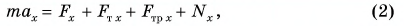
где 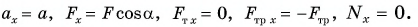
Тогда из уравнения (2) следует:
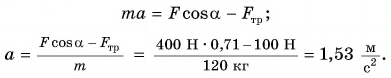
Ответ: 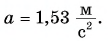
Пример №2
Два цилиндра — стальной и алюминиевый — одинакового объема подвешены к концам нити, перекинутой через неподвижный блок. Какой путь пройдет каждый цилиндр за время 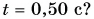 Силами сопротивления пренебречь. Блок считать невесомым, нить — невесомой и нерастяжимой. Принять
Силами сопротивления пренебречь. Блок считать невесомым, нить — невесомой и нерастяжимой. Принять 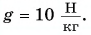
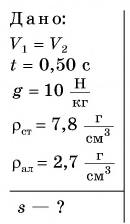
Решение
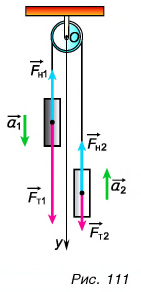
Сделаем рисунок к данной задаче (рис. 111).
На каждую гирю действуют сила тяжести 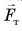 и сила натяжения нити
и сила натяжения нити 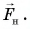
Согласно второму закону Ньютона:
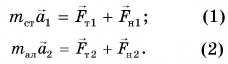
Модули сил тяжести 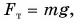 где
где 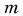 — масса груза. Так как нить нерастяжима,
— масса груза. Так как нить нерастяжима, 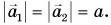
Так как блок и нити невесомы, 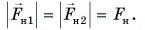
Запишем уравнения (1) и (2) в проекции на вертикальную ось Оу (см. рис. 111):

Вычтем из уравнения (3) уравнение (4), получим:
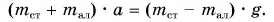
Отсюда
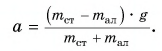
Массы цилиндров:

Тогда
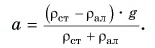
Путь, пройденный каждым из цилиндров:
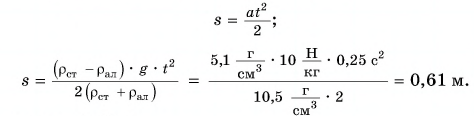
Ответ: 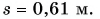
Третий закон Ньютона. Принцип относительности Галилея
Второй закон Ньютона объясняет, какое ускорение возникает при движении тела; на которое действуют другие тела. А действует ли при этом данное тело на эти тела?
Рассмотрим несколько примеров.
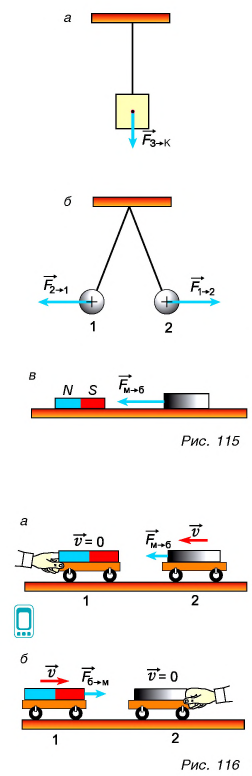
Земля притягивает кубик силой 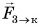 (рис. 115, а). Заряженный шар 1 отталкивает такой же заряженный шар 2 силой
(рис. 115, а). Заряженный шар 1 отталкивает такой же заряженный шар 2 силой 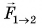 (рис. 115, б). Магнит притягивает железный брусок силой
(рис. 115, б). Магнит притягивает железный брусок силой 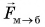 (рис. 115, в). Действует ли при этом кубик на Землю? Заряженный шар 2 на заряженный шар 1? Железный брусок па магнит? Если действует, то с какой силой?
(рис. 115, в). Действует ли при этом кубик на Землю? Заряженный шар 2 на заряженный шар 1? Железный брусок па магнит? Если действует, то с какой силой?
Ответ очевиден лишь для случая, представленного на рисунке 115, б. Заряженные шары 1 и 2 «равноправны». Модули сил 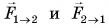 равны, а их направления противоположны, т. е.
равны, а их направления противоположны, т. е. 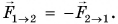 А если тела отличаются друг от друга (рис. 115, в)?
А если тела отличаются друг от друга (рис. 115, в)?
Проведем опыт. Поместим магнит на тележку 1, а железный брусок — на тележку 2 (рис. 116).
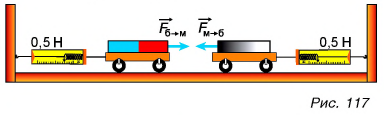
Будем удерживать тележку 1 с магнитом. Тележка 2 с бруском (рис. 116, а) поедет в сторону магнита. Удержим теперь тележку 2 (рис. 116, б), а тележку 1 с магнитом отпустим. Тележка с магнитом поедет в сторону бруска. Значит, и железный брусок притягивает к себе магнит.
Одинаковы ли модули сил, с которыми магнит и брусок притягивают друг друга? Это можно выяснить с помощью опытов. Равенство показаний динамометров (рис. 117) говорит о том, что модули этих сил равны: 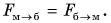
Результаты данных опытов не случайны. Механическое действие тел друг на друга всегда взаимно. Одностороннего действия не бывает. Существует лишь взаимодействие. При этом силы, с которыми тела действуют друг на друга, имеют равные модули, противоположные направления и лежат на одной прямой:
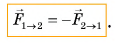
Это утверждение носит название третьего закона Ньютона. Он выполняется для тел любых масс, размеров, формы и состава вещества.
Что еще надо знать о силах взаимодействия?
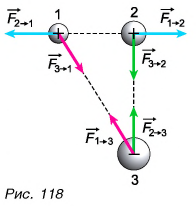
Силы взаимодействия приложены к разным телам (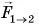 — к шару 2,
— к шару 2, 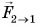 — к шару 1) (см. рис. 115, б). Поэтому они не могут компенсировать (уравновесить) друг друга.
— к шару 1) (см. рис. 115, б). Поэтому они не могут компенсировать (уравновесить) друг друга.
Силы взаимодействия всегда имеют одну и ту же природу (например, обе являются электрическими силами или обе — гравитационными и т. д.).
Если одновременно взаимодействует несколько тел (рис. 118), то равенство 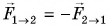 выполняется для каждой пары тел.
выполняется для каждой пары тел.
Третий закон Ньютона объясняет многие явления повседневной жизни. Так, для прыжка вверх (рис. 119) спортсмен отталкивает опору силой 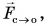 направленной вниз. Ответная (противодействующая) сила
направленной вниз. Ответная (противодействующая) сила 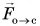 придает прыгуну направленное вверх ускорение.
придает прыгуну направленное вверх ускорение.
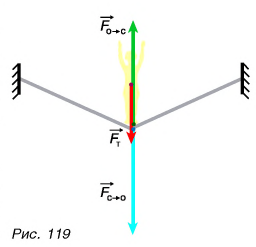
Человек при ходьбе, автомобиль при движении отталкиваются от дорожного покрытия. В ответ на это дорожное покрытие действует па них с силой, имеющей горизонтальную составляющую, направленную вперед. Лодка (рис. 120), корабль отталкиваются от воды, самолет — от воздуха (или от реактивной струи).
Мы рассмотрели законы Ньютона — основные законы механики.
Рассмотрим еще одно важное положение механики — принцип относительности Галилея.
Мы познакомились с понятиями «инерциальная система отсчета» и «неинерциальная система отсчета». Мы узнали, что если на тело не действуют силы (или действуют, но компенсируют друг друга), то:
- относительно инерциальных систем это тело покоится или движется равномерно и прямолинейно;
- относительно неинерциальных — движется с ускорением.
Значит, в инерциальных и неинерциальных системах механические явления происходят по-разному. Эти системы «неравноправны». А равноправны ли между собой инерциальные системы?
Опыты показывают, что относительно поезда, самолета, автобуса и т. д., имеющих в системе отсчета «Земля» постоянную скорость, любое тело ведет себя точно так же, как и относительно Земли.
На основе опытов был сделан вывод: во всех инерциальных системах отсчета механические явления при одинаковых условиях происходят одинаково.
Данное утверждение выражает равноправие всех инерциальных систем в механике. Оно носит название «принцип относительности Галилея».
Этот принцип можно сформулировать и иначе: «Никакими механическими опытами, проводимыми внутри любой инерциальной системы, нельзя установить, покоится она или движется».
Главные выводы:
- Действие тел друг на друга всегда взаимно.
- Силы взаимодействия двух тел имеют равные модули, направлены по одной прямой в противоположные стороны и имеют одинаковую природу (третий закон Ньютона).
- Силы взаимодействия двух тел не компенсируют друг друга, так как они приложены к разным телам.
- Во всех инерциальных системах все механические явления при одинаковых условиях происходят одинаковым образом (принцип относительности Галилея).
Деформация тел. Сила упругости. Закон Гука
До сих пор мы рассматривали модель абсолютно твердого тела. Размеры и форма тела в процессе его движения и взаимодействия не изменялись. Однако в ряде явлений происходит деформация тела, т. е. изменение его размеров, формы. Какими закономерностями описываются деформации?

Деформация происходит в результате перемещения одних частей тела относительно других. Па рисунке 125, а, б, в, г на модели показаны различные виды деформаций: сжатие, сдвиг, изгиб, кручение.
При сжатии (рис. 125, а) и растяжении изменяются расстояния между слоями. При сдвиге (рис. 125, б) слои смещаются относительно друг друга. Деформация изгиба (рис. 125, в) является комбинацией сжатия и растяжения. При деформации кручения (рис. 125, г) слои поворачиваются относительно друг друга.
Деформации возникают под действием приложенных к телу сил (рис. 125). Что будет, если действие сил прекратится?

Проведем опыт. Изогнем ластик (рис. 126, а). Он деформируется. Прекратим воздействие. Деформация исчезнет.
Если размеры и форма тела полностью восстанавливаются после прекращения действия силы, то деформацию называют упругой.
Деформируем теперь кусок пластилина (рис. 126, б). После прекращения действия силы его форма не восстановилась. Такую деформацию называют неупругой или пластической.

Пластической деформации подвергают металл при прокатке, ковке (рис. 127), штамповке и т. д.
Характер деформации зависит не только от вещества, из которого состоит тело, но и от того, насколько велика внешняя сила, как долго она действует, а также от температуры тела. Например, если железную пластину немного изогнуть и отпустить, она восстановит свою форму. Однако если ее закрепить в деформированном состоянии на длительное время, то после снятия внешней силы восстановление будет неполным.
Если же тело нагрето до высокой температуры, то деформация будет пластической даже под действием кратковременной силы (рис. 127).
Рассмотрим подробнее наиболее простую деформацию: упругое растяжение. Как величина деформации тела зависит от приложенной к нему силы?
Проведем опыт. Закрепим один конец резинового шнура, а к другому подвесим груз (рис. 128). Под действием деформирующей силы 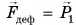 (веса груза) шнур растянется. Его длина станет больше начальной на величину
(веса груза) шнур растянется. Его длина станет больше начальной на величину 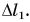 Будем увеличивать деформирующую силу, подвешивая два, три и т. д. одинаковых груза:
Будем увеличивать деформирующую силу, подвешивая два, три и т. д. одинаковых груза: 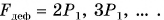
Удлинение шнура 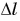 возрастает во столько же раз.
возрастает во столько же раз.
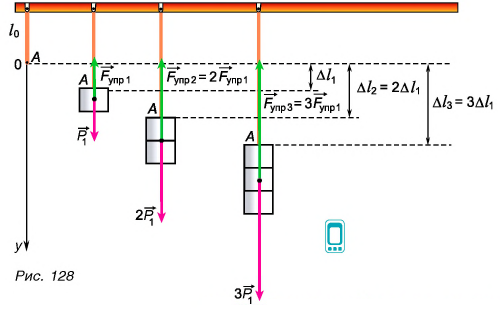
Проведем аналогичные опыты с пружиной (рис. 129). Ее можно как растягивать, так и сжимать. Результаты будут аналогичны: при упругих деформациях сжатия и растяжения изменение длины тела прямо пропорционально деформирующей силе:

Как при растяжении шнура, так и при сжатии пружины в ответ па действие деформирующей силы 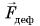 возникала противодействующая ей сила упругости
возникала противодействующая ей сила упругости 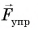 (рис. 128 и 129).
(рис. 128 и 129).
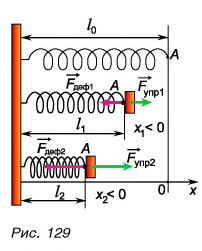
К чему приложена упругая сила? Куда она направлена? Каким закономерностям она подчиняется? Какова ее природа?
Рисунки 128 и 129 показывают: сила упругости приложена к телу, которое вызвало деформацию.
Согласно третьему закону Ньютона

Сила упругости направлена противоположно деформирующей силе, а их модули равны.
Из формул (1) и (2) следует:

где 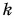 — постоянный коэффициент. Значит, при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален изменению длины тела.
— постоянный коэффициент. Значит, при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален изменению длины тела.
Это — закон Гука (установлен английским ученым Робертом Гуком в 1660 г.).
Коэффициент пропорциональности 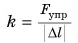 называется жесткостью тела.
называется жесткостью тела.
Жесткость тела численно равна модулю силы упругости, возникающей при удлинении (или сжатии) тела на единицу длины.
Единица жесткости в СИ — 1 ньютон на метр 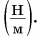
Для любознательных:
Жесткость тела зависит от материала, из которого оно изготовлено, от формы и размеров тела, от его температуры. Жесткость тела постоянного поперечного сечения (шнура, проволоки и т. д.) прямо пропорциональна площади сечения и обратно пропорциональна длине тела.
Из рисунков 128 и 129 видно, что и при растяжении, и при сжатии сила упругости направлена противоположно перемещению точки приложения деформирующей силы (точки А). С учетом этого закон Гука записывают в следующем виде:

где 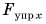 — проекция силы упругости на ось Ох, а х — координата точки А. Начало координат па оси Ох выбрано так, чтобы при
— проекция силы упругости на ось Ох, а х — координата точки А. Начало координат па оси Ох выбрано так, чтобы при 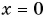 деформация отсутствовала.
деформация отсутствовала.
На рисунке 130, а, б представлены графики зависимости силы упругости от деформации 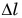 и от х. Прямолинейность графиков выражает прямую пропорциональную зависимость силы упругости от
и от х. Прямолинейность графиков выражает прямую пропорциональную зависимость силы упругости от 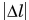 и от х.
и от х.
Не забывайте, что закон Гука, а значит, и формулы (3), (4) выполняются только для упругих деформаций!
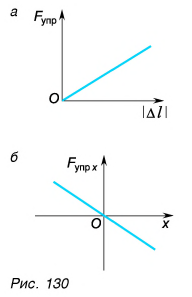
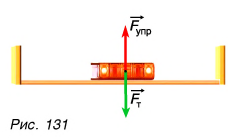
Все окружающие нас тела в той или иной степени деформированы. Хотя эти деформации чаще всего незаметны, связанные с ними силы упругости не малы. Например, сила упругости полки уравновешивает силу тяжести книги (рис. 131), сила упругости рельсов — силу тяжести поезда и т. д. Силу упругости, возникающую в ответ на действие тела на опору, называют силой реакции опоры. Силу упругости растянутой нити, веревки, троса и т. д. — силой натяжения.
Почему при деформации возникают силы упругости? Какова их природа?
Из 7-го класса вам известно, что тела состоят из молекул, которые взаимодействуют друг с другом, и что силы взаимодействия имеют электромагнитное происхождение. Свойства этих сил таковы, что на определенном расстоянии 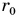 между молекулами сила их взаимодействия обращается в нуль, при
между молекулами сила их взаимодействия обращается в нуль, при 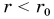 молекулы отталкивают друг друга, а при
молекулы отталкивают друг друга, а при 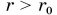 — притягивают.
— притягивают.
Поэтому при сжатии тела силы взаимодействия молекул препятствуют его сжатию, а при растяжении — растяжению.
Силы упругости возникают из-за взаимодействия молекул между собой и имеют электромагнитную природу.
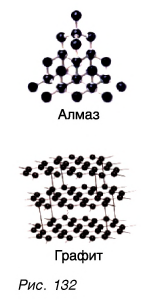
И упругие, и пластические свойства тел определяются тем, из каких молекул тела состоят и как расположены молекулы по отношению друг к другу. На рисунке 132 изображены кристаллические решетки алмаза и графита (разновидностей углерода). Различное расположение одних и тех же атомов углерода приводит к резким отличиям свойств данных веществ.
Главные выводы:
- Изменение размеров или формы тела называется деформацией.
- Если после прекращения действия внешних сил размеры и форма тела полностью восстанавливаются, то деформация называется упругой. Если восстанавливаются не полностью, то — пластической.
- Силы упругости направлены противоположно деформирующим силам.
- При упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
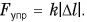
Пример №3
Под действием пружинного динамометра железный кубик с длиной ребра 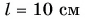 движется по гладкой горизонтальной поверхности с постоянным ускорением, модуль которого
движется по гладкой горизонтальной поверхности с постоянным ускорением, модуль которого 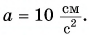 Определите удлинение пружины динамометра жесткостью
Определите удлинение пружины динамометра жесткостью 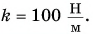

Решение
Сделаем рисунок к задаче (рис. 133).
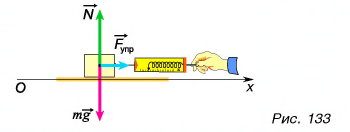
По условию задачи на кубик действуют: сила тяжести 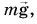 сила реакции
сила реакции 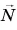 и сила упругости пружины динамометра
и сила упругости пружины динамометра 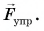 Трение отсутствует. По второму закону Ньютона:
Трение отсутствует. По второму закону Ньютона:
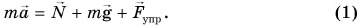
В проекции на ось Ох:

Масса кубика 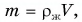 где объем кубика
где объем кубика 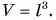 Тогда
Тогда

Модуль силы упругости пружины динамометра по закону Гука:

Подставив выражения (3) и (4) в выражение (2), получим:
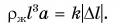
Отсюда 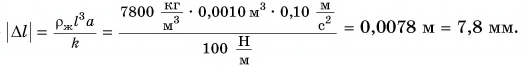
Ответ: 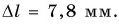
Силы трения. Силы сопротивления среды
Согласно первому закону Ньютона для движения с постоянной скоростью силы не нужны. Почему же движущиеся санки, лодка, шайба и т. д. останавливаются, если мы перестаем действовать на них силой? Какие силы препятствуют их движению?
Санки и шайбу останавливает сила трения скольжения у лодку — сила сопротивления среды.
Рассмотрим силу трения скольжения. Она возникает при перемещении одного тела по поверхности другого.
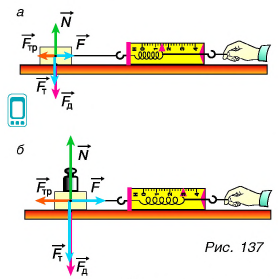
Проведем опыт. С помощью динамометра будем перемещать деревянный брусок по поверхности стола (рис. 137, а). На брусок действуют сила тяжести 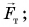 сила реакции опоры
сила реакции опоры 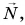 компенсирующая силу тяжести, сила упругости пружины динамометра
компенсирующая силу тяжести, сила упругости пружины динамометра 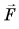 и сила трения
и сила трения 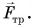 При равномерном перемещении бруска модули сил
При равномерном перемещении бруска модули сил 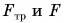 равны.
равны.
С помощью гири увеличим силу давления 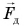 бруска на стол (рис. 137, б). Сила трения тоже возрастает. При увеличении силы давления в
бруска на стол (рис. 137, б). Сила трения тоже возрастает. При увеличении силы давления в 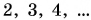 раза показания динамометра F увеличиваются также в
раза показания динамометра F увеличиваются также в 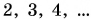 раза. Значит, модуль силы трения скольжения прямо пропорционален модулю силы давления тела на опору:
раза. Значит, модуль силы трения скольжения прямо пропорционален модулю силы давления тела на опору:

где 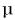 — коэффициент трения скольжения. Он зависит от свойств соприкасающихся поверхностей, от их шероховатости, от наличия примесей и загрязнений.
— коэффициент трения скольжения. Он зависит от свойств соприкасающихся поверхностей, от их шероховатости, от наличия примесей и загрязнений.
Приведем приближенные значения коэффициентов трения для некоторых материалов (табл. 2).
Таблица 2. Коэффициенты трении скольжения

Сила давления 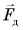 действует со стороны бруска на стол, а сила
действует со стороны бруска на стол, а сила 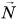 — со стороны стола на брусок. Направления этих сил противоположны (рис. 137), а их модули, по третьему закону Ньютона, равны
— со стороны стола на брусок. Направления этих сил противоположны (рис. 137), а их модули, по третьему закону Ньютона, равны 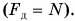 Поэтому вместо формулы (1) часто используют формулу
Поэтому вместо формулы (1) часто используют формулу

Так как сила 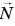 направлена по нормали к поверхности опоры, ее следует называть нормальной реакцией опоры.
направлена по нормали к поверхности опоры, ее следует называть нормальной реакцией опоры.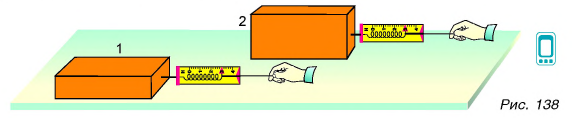
Зависит ли сила трения скольжения от площади соприкосновения тел? Сравним силу трения при двух положениях 1 и 2 бруска (рис. 138). Хотя площадь контакта бруска с доской в положении 2 меньше, показания динамометра почти не изменились. Значит, сила трения практически не зависит от площади соприкосновения тел.
Куда направлена сила трения скольжения?
Опыты, показанные на рисунке 137, свидетельствуют, что сила трения скольжения направлена противоположно скорости движения тела относительно опоры.
Для любознательных:
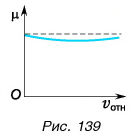
Отметим, что коэффициент трения скольжения 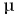 незначительно зависит от скорости движения тела относительно опоры
незначительно зависит от скорости движения тела относительно опоры 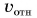 (рис. 139). При решении задач, как правило, принимают
(рис. 139). При решении задач, как правило, принимают 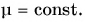
А может ли сила трения действовать на неподвижное тело? Рассмотрим пример. Шкаф стоит на горизонтальном полу (рис. 140). На него действуют две силы: сила тяжести 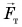 и сила реакции опоры
и сила реакции опоры 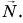 Они уравновешивают друг друга. Сила трения равна нулю.
Они уравновешивают друг друга. Сила трения равна нулю.
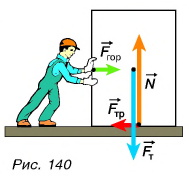
Приложим к шкафу внешнюю силу 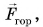 параллельную полу. Шкаф по-прежнему в состоянии покоя. Значит, есть сила, компенсирующая силу
параллельную полу. Шкаф по-прежнему в состоянии покоя. Значит, есть сила, компенсирующая силу 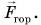 Этой силой является сила трения покоя
Этой силой является сила трения покоя 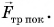
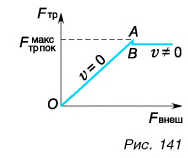
При увеличении внешней силы растет и сила трения покоя (рис. 141), пока шкаф не сдвинется с места. В этот момент сила трения покоя достигает своего максимального значения 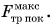 Оно, как показывает опыт, прямо пропорционально модулю силы давления
Оно, как показывает опыт, прямо пропорционально модулю силы давления 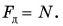
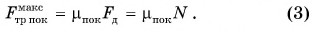
Коэффициент трения покоя 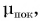 как правило, немного больше, чем коэффициент трения скольжения
как правило, немного больше, чем коэффициент трения скольжения 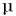 (рис. 141). Поэтому тело труднее сдвинуть с места, чем затем его перемешать.
(рис. 141). Поэтому тело труднее сдвинуть с места, чем затем его перемешать.
Сила трения покоя направлена противоположно горизонтальной составляющей внешней силы, стремящейся сдвинуть тело. Это следует из условия равновесия 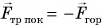 (рис. 140).
(рис. 140).

А какой будет сила трения при качении тела?
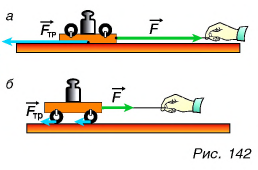
Опыт показывает, что при замене скольжения качением (рис. 142, а, б) сила трения уменьшается (в десятки раз — для дерева по дереву, почти в 100 раз — для стали по стали и т. д.).
Трение играет очень важную роль в технике и в повседневной жизни. Так, при отсутствии трения любой предмет соскользнул бы с полки при малейшем ее наклоне. И автомобиль, и пешеход не смогли бы ни начать движение, ни остановиться. Поэтому трение часто стремятся увеличить. Обувь и автопокрышки делают рельефными (рис. 143, а), дорогу зимой посыпают песком и т. д.
В то же время трение деталей при работе механизмов (валов в подшипниках, шарнирных соединений и т. д.) является вредным. Оно приводит к износу и нагреванию деталей, к потерям энергии. В таких случаях трение стремятся уменьшить. Трущиеся поверхности шлифуют, на них наносят специальные смазки, скольжение заменяют качением (рис. 143, б).
Рассмотрим движение тела в жидкости или газе. Здесь тоже есть силы, препятствующие движению. Их называют силами сопротивления. Силы сопротивления в жидкости и газе возникают только при движении тела и среды друг относительно друга.
Значит, сила трения покоя в жидкостях и газах равна нулю.
Поэтому человек, который не смог бы сдвинуть с места лежащую на берегу лодку, легко приведет ее в движение в воде.
От чего зависит сила сопротивления? Выяснить это можно на опытах, измеряя по показаниям динамометра силу, с которой поток газа или жидкости действует на тело (рис. 144).
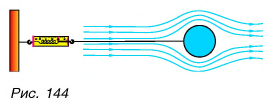
Опыты показывают, что сила сопротивления зависит от следующих факторов.
1. От свойств среды: для данного тела при одной и той же скорости сила сопротивления в воздухе намного меньше, чем в воде, в воде — меньше, чем в сахарном сиропе, и т. д.
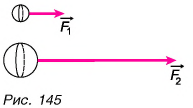
2. От размеров тела: сила сопротивления прямо пропорциональна площади их поперечного сечения (рис. 145).
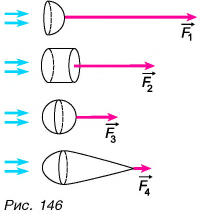
3. От формы тела: у тел на рисунке 146 одинаковая площадь поперечного сечения, но разная форма. Наибольшую силу сопротивления испытывает вогнутая полусфера, а наименьшую — тело каплевидной (обтекаемой) формы.
Обтекаемая форма тела у птиц и рыб сводит до минимума силу сопротивления воздуха или воды и тем самым облегчает их движение. С той же целью обтекаемую форму придают самолетам (рис. 147, а), речным и морским судам, подводным лодкам (рис. 147, б) и т. д.
Чем обусловлена форма парашюта (рис. 147, в)? Объясните самостоятельно.
4. От скорости движения: сила сопротивления возрастает с увеличением скорости движения тела относительно среды. При малых скоростях она растет прямо пропорционально модулю скорости, а при больших — квадрату модуля скорости и даже быстрее.
Силы трения и сопротивления среды (как и силы упругости) определяются взаимодействием молекул и, следовательно, имеют электромагнитную природу.

Главные выводы:
- Сила трения скольжения прямо пропорциональна силе давления и направлена против скорости движения тела.
- Коэффициент трения скольжения зависит от материалов и состояния соприкасающихся поверхностей, но практически не зависит от их площади.
- Сила трения качения существенно меньше силы трения скольжения.
- Сила трения покоя возникает при наличии внешней силы, стремящейся вызвать движение тела.
- Силы сопротивления движению тела в газе или жидкости зависят от свойств среды, размеров и формы тела и от скорости его движения.
Пример №4
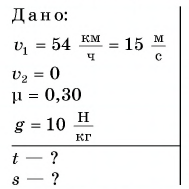
Автомобиль, имея скорость, модуль которой 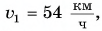 тормозит на горизонтальном участке дороги до полной остановки. Коэффициент трения скольжения
тормозит на горизонтальном участке дороги до полной остановки. Коэффициент трения скольжения 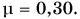 Приняв
Приняв 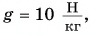 определите время торможения и тормозной путь.
определите время торможения и тормозной путь.
Решение
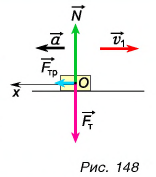
Изобразим силы, действующие на автомобиль(рис. 148).
Сила тяжести 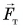 и сила реакции опоры
и сила реакции опоры 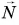 компенсируют друг друга. Результирующая всех сил, приложенных к автомобилю, равна силе трения. По второму закону Ньютона
компенсируют друг друга. Результирующая всех сил, приложенных к автомобилю, равна силе трения. По второму закону Ньютона 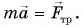 В проекции на ось Ох:
В проекции на ось Ох: 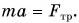
Поскольку 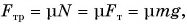 модуль ускорения
модуль ускорения 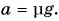 Учитывая, что
Учитывая, что 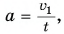 получим:
получим: 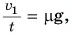 откуда
откуда 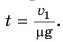
Подставив численные значения, находим: 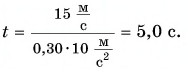
Тормозной путь: 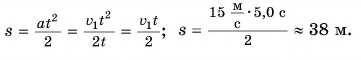
Ответ: 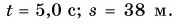
Движение тела под действием силы тяжести
Законы падения тел интересовали людей с древних времен. Считалось очевидным, что тяжелые тела падают быстрее легких. А что показывает опыт?
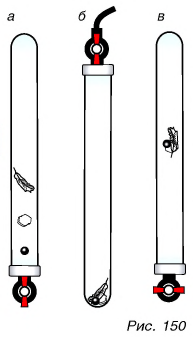
Поместим на дно стеклянной трубки дробинку, кусочек пробки и птичье перышко. Перевернем трубку. Быстрее всех падает дробинка, медленнее всех — перышко (рис. 150, а). Означает ли это, что тяжелые тела надают быстрее легких? Не торопитесь с ответом. Откачаем из трубки воздух (рис. 150, б) и перевернем ее снова (рис. 150, в). Теперь дробинка, пробка и перышко достигают дна одновременно!
Тела падают по-разному не из-за различия масс, а из-за различия действующих на них сил сопротивления воздуха. Такой вывод сделал Галилей еще в XVI в.
Движение тела, на которое действует только сила тяжести, называется свободным падением.
Почему свободно падавшие дробинка, пробка, перышко двигались одинаково?
Найдем ускорение свободного падения 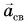 тела массой
тела массой 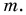 На него действует только сила тяжести
На него действует только сила тяжести 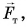 модуль которой равен
модуль которой равен 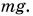 По второму закону Ньютона
По второму закону Ньютона 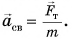 Значит, ускорение всех свободно падающих тел направлено по вертикали вниз, а его модуль
Значит, ускорение всех свободно падающих тел направлено по вертикали вниз, а его модуль

Ускорение свободного падения для всех тел (в данном месте) одинаково.
В чем причина такой удивительной закономерности? В том, что масса является одновременно:
- мерой гравитационных свойств тел (сила тяжести прямо пропорциональна массе);
- мерой инертности тел (ускорение обратно пропорционально массе) (см. § 16).
Именно поэтому в формуле (1) масса 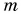 попадает и в числитель, и в знаменатель и сокращается.
попадает и в числитель, и в знаменатель и сокращается.
В 7-м классе коэффициент 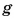 мы выражали в
мы выражали в 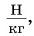 а согласно формуле (1)
а согласно формуле (1) 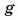 измеряется в
измеряется в 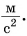 В этом нет противоречия. Докажите самостоятельно, что
В этом нет противоречия. Докажите самостоятельно, что 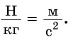
Для любознательных:
На широте Минска 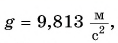 па экваторе —
па экваторе — 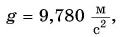 на полюсах —
на полюсах — 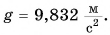 Причиной зависимости ускорения свободного падения от географической широты является вращение Земли вокруг своей оси, а также «сплюснутость» Земли у полюсов. При удалении от поверхности Земли ускорение свободного падения постепенно уменьшается.
Причиной зависимости ускорения свободного падения от географической широты является вращение Земли вокруг своей оси, а также «сплюснутость» Земли у полюсов. При удалении от поверхности Земли ускорение свободного падения постепенно уменьшается.
Характеристики движения свободно падающих тел (траектория, время полета и т. д.) зависят от положения точки бросания и от начальной скорости.
Рассмотрим различные движения металлического шарика: а) вертикально вниз (рис. 151); б) горизонтально (рис. 152).
1. Шарик падает с высоты h без начальной скорости 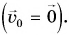 Движение шарика будет прямолинейным, равноускоренным (рис. 151). Проекция скорости
Движение шарика будет прямолинейным, равноускоренным (рис. 151). Проекция скорости 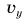 на ось Оу и координата равны:
на ось Оу и координата равны:

Из формул (2) можно определить любую характеристику движения шарика. Например, приравнивая 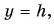 находим время падения:
находим время падения: 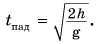 Затем, подставляя t в формулу для
Затем, подставляя t в формулу для 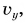 определяем скорость шарика в конце падения:
определяем скорость шарика в конце падения: 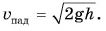
2. Шарик брошен горизонтально. Из рисунка 152 видно, что шарик, брошенный горизонтально, движется по криволинейной траектории ОВ. При этом он участвует одновременно в двух движениях: переметается вправо по горизонтали и снижается по вертикали.
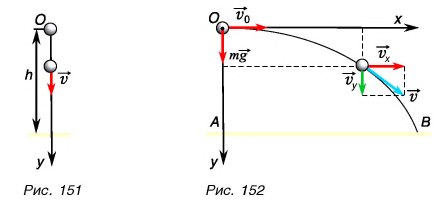
Для описания движения шарика введем две координатные оси (Ох и Оу). Во время полета на шарик действует одна постоянная сила 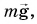 направленная но оси Оу. Следовательно, проекции ускорения шарика:
направленная но оси Оу. Следовательно, проекции ускорения шарика:

В результате:
- проекция скорости движения шарика
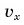 и его координата х изменяются по законам равномерного движения с начальной скоростью
и его координата х изменяются по законам равномерного движения с начальной скоростью 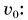

- проекция скорости
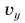 и координата у — но законам равноускоренного движения без начальной скорости. Для них выполняются те же формулы (2), что и для шарика в предыдущем примере.
и координата у — но законам равноускоренного движения без начальной скорости. Для них выполняются те же формулы (2), что и для шарика в предыдущем примере.
Отсюда следует вывод. Время полета шарика в случаях, изображенных на рисунках 151 и 152, одинаково! Оно равно 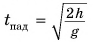 и не зависит от начальной скорости.
и не зависит от начальной скорости.
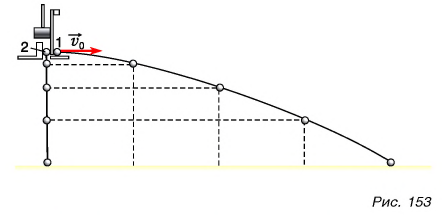
Подтвердим это опытом с помощью установки, показанной на рисунке 153. В результате удара молотком по пластине шарик 1 приобретает горизонтальную начальную скорость 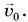 В тот же момент шарик 2 начинает падение по вертикали без начальной скорости. Шарики достигают горизонтальной поверхности одновременно.
В тот же момент шарик 2 начинает падение по вертикали без начальной скорости. Шарики достигают горизонтальной поверхности одновременно.
Дополнительную информацию дают фотографии шариков, сделанные через равные промежутки времени (рис. 153). Они подтверждают, что движение обоих шариков по вертикали было равноускоренным (и одинаковым), а движение шарика 1 но горизонтали — равномерным.
Найдем горизонтальную дальность полета шарика — расстояние 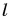 от точки А до места падения шарика — точки В (см. рис. 152). Из рисунка видно, что расстояние
от точки А до места падения шарика — точки В (см. рис. 152). Из рисунка видно, что расстояние 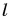 равно значению координаты х в момент падения:
равно значению координаты х в момент падения:
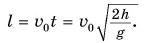
Скорость движения шарика в каждой точке направлена но касательной к траектории. С помощью формул (2) и (3) находим зависимость модуля скорости от времени: 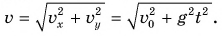 В конце полета
В конце полета 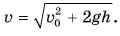 Докажите это самостоятельно.
Докажите это самостоятельно.
Определим теперь форму траектории. Выразим время t из формулы (3) 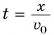 и подставим его в выражение для у из формулы (2)
и подставим его в выражение для у из формулы (2) 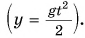 Находим:
Находим: 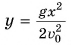 (уравнение параболы). Следовательно, траектория движения тела, брошенного горизонтально, есть участок параболы с вершиной в точке бросания.
(уравнение параболы). Следовательно, траектория движения тела, брошенного горизонтально, есть участок параболы с вершиной в точке бросания.
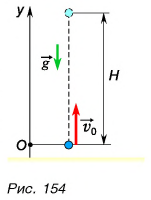
3. Шарик брошен вертикально вверх. Шарик при подъеме движется прямолинейно и равнозамедленно (рис. 154). Проекция скорости движения 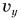 и координата у шарика определяются по формулам
и координата у шарика определяются по формулам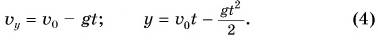
Приравнивая 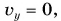 находим время подъема:
находим время подъема: 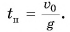 Приравнивая
Приравнивая 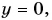 получаем полное время полета:
получаем полное время полета: 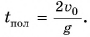 Подставляя
Подставляя 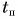 в формулу для координаты у из формулы (4), определяем максимальную высоту подъема:
в формулу для координаты у из формулы (4), определяем максимальную высоту подъема: 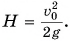
Главные выводы:
- Свободным падением называют движение тела, на которое действует только сила тяжести.
- Ускорения всех свободно падающих тел в данном месте одинаковы. Вблизи поверхности Земли модуль ускорения свободного падения постоянен и равен
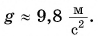
- Свободно падающее тело участвует одновременно в двух движениях: в равнопеременном по вертикали и в равномерном — по горизонтали.
- Траектория движения тела, брошенного горизонтально, является участком параболы (если сопротивлением воздуха можно пренебречь).
Пример №5
С балкона десятого этажа девочка бросила своему брату связку ключей, придав ей начальную скорость 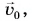 направленную вертикально вниз. К моменту приземления скорость связки стала равной
направленную вертикально вниз. К моменту приземления скорость связки стала равной 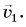 Определите высоту, с которой были сброшены ключи, и время их падения, если
Определите высоту, с которой были сброшены ключи, и время их падения, если 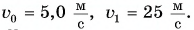 Сопротивление воздуха не учитывать;
Сопротивление воздуха не учитывать; 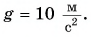

Решение
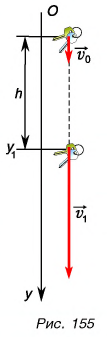
Сделаем рисунок к задаче (рис. 155). Скорость 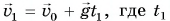 — время падения. В проекции на ось Оу получим:
— время падения. В проекции на ось Оу получим: 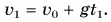 Тогда время падения:
Тогда время падения:
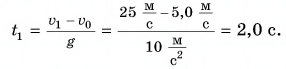
Высота, с которой сброшены ключи, равна значению координаты у в момент их приземления:
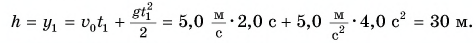
Ответ: 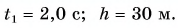
Пример №6
Стоящий на берегу мальчик бросает в озеро камешек. Точка бросания находится на высоте 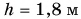 над поверхностью воды. Начальная скорость камешка
над поверхностью воды. Начальная скорость камешка 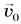 направлена горизонтально. Камешек падает в воду на расстоянии
направлена горизонтально. Камешек падает в воду на расстоянии 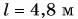 от берега. Определите время полета камешка, модуль его начальной скорости и модуль скорости, с которой он вошел в воду. Сопротивление воздуха не учитывать;
от берега. Определите время полета камешка, модуль его начальной скорости и модуль скорости, с которой он вошел в воду. Сопротивление воздуха не учитывать; 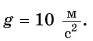
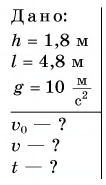
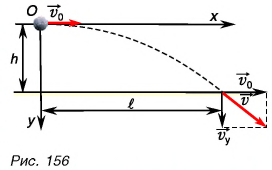
Решение
Сделаем рисунок к задаче (рис. 156). Камешек участвует одновременно в двух движениях: равномерном со скоростью 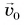 по горизонтами и равноускоренном без начальной скорости по вертикали. В конце полета проекции скорости на оси Ох и Оу и координаты камешка:
по горизонтами и равноускоренном без начальной скорости по вертикали. В конце полета проекции скорости на оси Ох и Оу и координаты камешка:
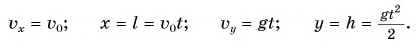
Отсюда
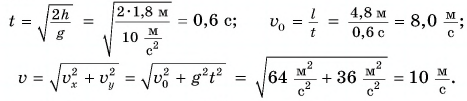
Ответ: 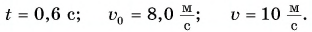
Движение тела, брошенного под углом к горизонту
Рассмотрим движение тела, брошенного под углом к горизонту. Такое движение совершают, например, волейбольный мяч; артиллерийский снаряд и др.
Моделью движения тела, брошенного под углом к горизонту, может служить движение капель, образующих водяную струю. Проведем опыт на установке, показанной на рисунке 157. В открытом сосуде находится подкрашенная вода. Струя образуется с помощью гибкого шланга, снабженного наконечником. Для определения формы траектории капель форму струи можно сравнить с кривыми, заранее нарисованными на листе картона.
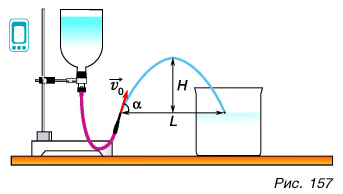
Выясним на опыте, как начальная скорость капель влияет на максимальную высоту Н и дальность L их полета.
Не изменяя угла вылета капель а, увеличим их начальную скорость, поднимая выше сосуд с водой. Высота Н и дальность полета L также будут увеличиваться.
Затем, не изменяя модуль начальной скорости, будем увеличивать угол а вылета капель от 0° до 90°. Сравнение формы струи с кривыми, нарисованными на картоне, укажет на сходство траекторий капель с параболами. Опыт показал, что высота и дальность полета, а также дальность траектории тела, брошенного под углом к горизонту, зависят от угла бросания и от начальной скорости.
А что показывают расчеты? Тело, брошенное под углом к горизонту, участвует одновременно в движении по вертикали и по горизонтали. Если сопротивлением воздуха можно пренебречь, то движение по вертикали будет равнопеременным с начальной скоростью 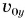 , а по горизонтали — равномерным со скоростью
, а по горизонтали — равномерным со скоростью 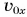 (рис. 158).
(рис. 158).
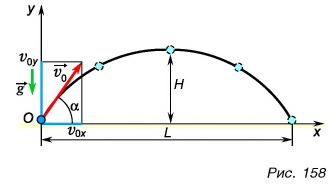
Тогда зависимости от времени для проекций скорости и координат тела на оси 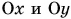 имеют вид:
имеют вид:
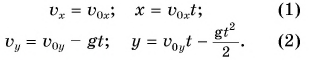
Из рисунка 158 видно, что 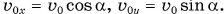 Поэтому максимальная высота Ну время подъема на эту высоту
Поэтому максимальная высота Ну время подъема на эту высоту 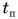 и время полета
и время полета 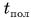 определяются формулами для равнопеременного движения тела, брошенного вертикально вверх с начальной скоростью
определяются формулами для равнопеременного движения тела, брошенного вертикально вверх с начальной скоростью 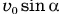 :
:
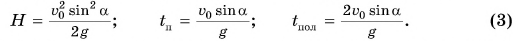
Умножив проекцию скорости 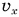 на время полета
на время полета 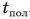 , получим горизонтальную дальность полета:
, получим горизонтальную дальность полета:
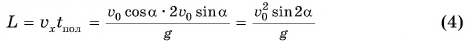
(при выводе формулы (4) использовалось тригонометрическое соотношение 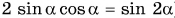 ).
).
Формула (4) показывает: максимальная дальность полета 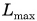 достигается при
достигается при 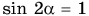 (т. е. при угле бросания a = 45°), дальность полета прямо пропорциональна квадрату начальной скорости.
(т. е. при угле бросания a = 45°), дальность полета прямо пропорциональна квадрату начальной скорости.
Для любознательных:
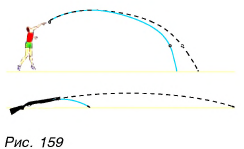
Влияние сопротивления воздуха на движение тел большой массы и малых размеров при небольших скоростях невелико (брошенный камень, спортивное ядро и др.). В других случаях, например для волейбольного мяча, ружейной пули и т. д., сопротивление воздуха весьма существенно. На рисунке 159 изображены траектории реального движения (сплошные линии) и траектории движения без учета сопротивления воздуха (штриховые линии): а) для спортивного ядра; б) для ружейной пули.
Главные выводы
Если сопротивлением воздуха можно пренебречь, то:
- Тело, брошенное под углом к горизонту, движется с постоянным ускорением по вертикали и равномерно — по горизонтали.
- Траектория движения тела, брошенного под углом к горизонту, является параболой.
Закон всемирного тяготения
В 7-м классе вы узнали о всемирном тяготении. Силами тяготения (гравитационными силами) притягивают друг друга все физические тела: атомы, молекулы, тела обычных размеров, планеты, звезды. Почему мы не замечаем взаимного притяжения окружающих нас предметов? С какой силой Солнце притягивает Землю?
Ответы на такие вопросы дает закон всемирного тяготения, сформулированный И. Ньютоном в 1667 г.
Все тела притягивают друг друга силами, прямо пропорциональными произведению масс этих тел и обратно пропорциональными квадрату расстояния между ними:

где 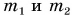 — массы тел, г — расстояние между телами, G — гравитационная постоянная.
— массы тел, г — расстояние между телами, G — гравитационная постоянная.
Формула (1) дает точное значение F для материальных точек и однородных тел, имеющих форму шара (для них г — расстояние между центрами). Силу тяготения для тел произвольной формы вычисляют, условно разбивая каждое тело на малые части и суммируя силы притяжения частей одного тела к частям другого.
Силы тяготения 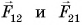 (рис. 160) направлены по линии, соединяющей тела, в противоположные стороны. Модули сил равны:
(рис. 160) направлены по линии, соединяющей тела, в противоположные стороны. Модули сил равны:
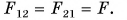
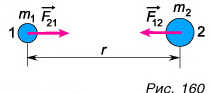
Согласно формуле (1) гравитационная постоянная G численно равна силе притяжения двух материальных точек массами по 1 кг, находящихся на расстоянии 1 м друг от друга.
Значение гравитационной постоянной можно определить экспериментально. Впервые такой опыт был проведен Генри Кавендишем в 1798 г.
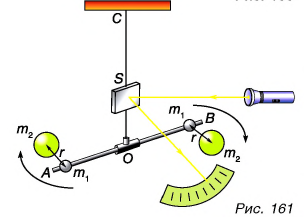
Схема установки представлена па рисунке 161. На стержне АС закреплены два одинаковых свинцовых шарика массой 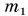 - 775 г. Стержень подвешен на тонкой упругой металлической нити ОС с легким зеркальцем S. Такое устройство называется крутильными весами.
- 775 г. Стержень подвешен на тонкой упругой металлической нити ОС с легким зеркальцем S. Такое устройство называется крутильными весами.
Притяжение шариков к тяжелым неподвижным свинцовым шарам массами 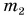 = 49,5 кг вызывает поворот стержня АВ и закручивание нити ОС. Угол закручивания чрезвычайно мал. Его определяли с помощью луча света, отраженного от зеркальца S, и шкалы. По углу закручивания нити находили силу притяжения.
= 49,5 кг вызывает поворот стержня АВ и закручивание нити ОС. Угол закручивания чрезвычайно мал. Его определяли с помощью луча света, отраженного от зеркальца S, и шкалы. По углу закручивания нити находили силу притяжения.
Зная массы 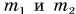 , расстояние r (см. рис. 161) и модуль силы притяжения F, по формуле (1) можно найти гравитационную постоянную
, расстояние r (см. рис. 161) и модуль силы притяжения F, по формуле (1) можно найти гравитационную постоянную 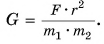 Современные эксперименты дают значение
Современные эксперименты дают значение 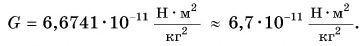
Значение гравитационной постоянной крайне мало. В связи с этим мала и сила притяжения окружающих нас тел друг к другу. Силы же притяжения этих тел к Земле не малы, потому что масса Земли огромна (около 6 • 1024 кг).
Закон всемирного тяготения объясняет многое в окружающем мире. С помощью данного закона можно найти ускорение свободного падения тел на разных планетах, определить массу Солнца, Земли и других планет, вычислить скорость движения орбитальной станции и т. д.
Ускорение свободного падения на планетах
Мы знаем, что на поверхности Земли 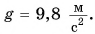 Чему оно равно на других планетах?
Чему оно равно на других планетах?
Рассмотрим тело массой т, находящееся на расстоянии г от центра планеты массой М и радиусом R (рис. 162). Сила притяжения 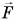 тела к планете придает ему ускорение
тела к планете придает ему ускорение 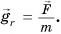 Из закона всемирного тяготения
Из закона всемирного тяготения 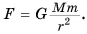 Тогда
Тогда 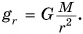
Так как 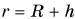 , где h — расстояние до поверхности планеты, то:
, где h — расстояние до поверхности планеты, то:

С ростом высоты h ускорение свободного падения убывает. На поверхности планеты, т. е. при h = 0, согласно формуле (2)
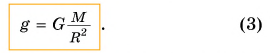
Ускорение свободного падения на поверхности планеты прямо пропорционально массе планеты и обратно пропорционально квадрату ее радиуса.
Для любознательных:
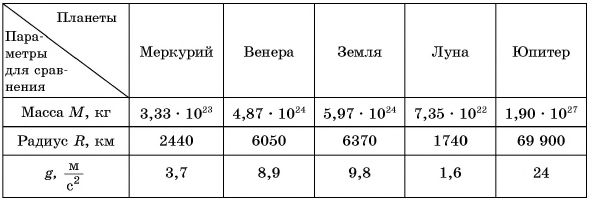
Рассмотрите таблицу 3 и сравните ускорение свободного падения на Юпитере и на Луне с ускорением g па Земле.
Таблица 3. Массы, радиусы и ускорения свободного падения для некоторых планет и их спутников
«Взвешивание» Земли. Выразим из формулы (3) массу планеты:

Из формулы (4) следует: зная ускорение свободного падения на поверхности планеты, ее радиус и гравитационную постоянную, можно определить массу планеты. Например, масса Земли
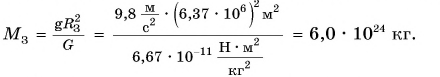
Скорость движения спутника Земли но круговой орбите. За пределами атмосферы силы сопротивления движению спутника отсутствуют. На него действует только сила притяжения к Земле. Поэтому спутник движется с ускорением 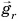 . Оно направлено к центру орбиты и является центростремительным ускорением:
. Оно направлено к центру орбиты и является центростремительным ускорением: 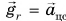 (рис. 163).
(рис. 163).
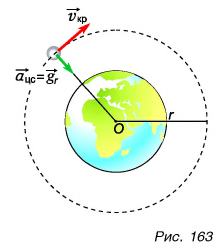
Как мы знаем из кинематики, 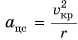 , где
, где 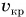 — скорость движения спутника по круговой орбите. Следовательно,
— скорость движения спутника по круговой орбите. Следовательно, 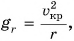 откуда
откуда
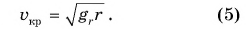
Скорость движения тела по круговой орбите, близкой к поверхности планеты (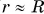 ), называется первой космической скоростью. Из формулы (5) значение первой космической скорости для Земли:
), называется первой космической скоростью. Из формулы (5) значение первой космической скорости для Земли:
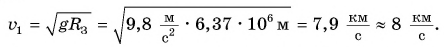
Второй космической скоростью 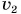 называют наименьшую начальную скорость, приобретя которую тело сможет покинуть планету. Можно доказать, что
называют наименьшую начальную скорость, приобретя которую тело сможет покинуть планету. Можно доказать, что 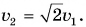 Для Земли
Для Земли 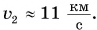
Скорость движения но круговой орбите радиусом г можно выразить через массу планеты и радиус орбиты. Подставляя gr из формулы (2) в формулу (5), получим:

Видно, что скорость 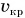 уменьшается при увеличении радиуса орбиты.
уменьшается при увеличении радиуса орбиты.
Из формулы (6) можно найти массу М. Значит, спутники планет могут «рассказать» о массе планеты, а планеты — о массе Солнца!
Главные выводы:
- Все тела притягивают друг друга силами, прямо пропорциональными произведению масс этих тел и обратно пропорциональными квадрату расстояния между ними.
- Гравитационная постоянная показывает, с какой силой притягиваются две материальные точки массами по 1 кг на расстоянии 1 м друг от друга.
- Ускорение свободного падения на поверхности планеты прямо пропорционально ее массе и обратно пропорционально квадрату радиуса планеты.
Пример №7
Геостационарным называют спутник, постоянно находящийся над определенной точкой поверхности Земли. Такие спутники широко используются как спутники связи. Определите радиус орбиты геостационарного спутника и его высоту над поверхностью Земли.
Решение
Орбита геостационарного спутника — окружность, лежащая в экваториальной плоскости Земли (рис. 164). Период обращения такого спутника совпадает с периодом вращения Земли вокруг своей оси (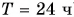 ).
).
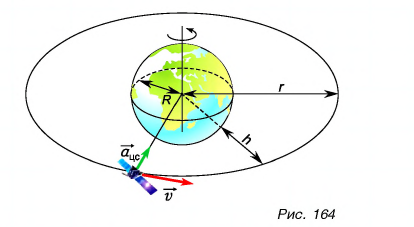
Хотя геостационарный спутник неподвижен относительно Земли, он движется ускоренно относительно инерциальной системы, связанной со звездами. Его центростремительное ускорение (рис. 164) 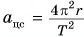 создано силой тяготения Земли. Приравнивая
создано силой тяготения Земли. Приравнивая 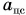 к ускорению свободного падения
к ускорению свободного падения 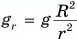 получим:
получим:
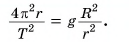
Отсюда радиус орбиты 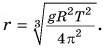 Подставляя
Подставляя 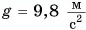 , радиус Земли
, радиус Земли 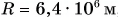 , период обращения
, период обращения 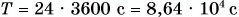 , находим:
, находим: 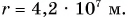 При таком радиусе орбиты расстояние до поверхности Земли составит:
При таком радиусе орбиты расстояние до поверхности Земли составит: 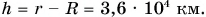
Ответ: 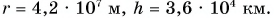
Невесомость и перегрузки
Всегда ли вес равен силе тяжести? При каких условиях наступает невесомость? Можно ли испытать состояние невесомости, не отправляясь в космос?
В 7-м классе вы узнали, что вес тела — это сила, с которой тело действует на опору или на подвес из-за притяжения к Земле.
Вес нельзя путать с силой тяжести. Сила тяжести 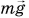 — это сила тяготения, действующая со стороны Земли на тело. Она приложена к телу в его центре тяжести (рис. 165, а, б).
— это сила тяготения, действующая со стороны Земли на тело. Она приложена к телу в его центре тяжести (рис. 165, а, б).
Вес 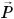 — сила, с которой тело действует на опору или на подвес. Он приложен к опоре или к подвесу.
— сила, с которой тело действует на опору или на подвес. Он приложен к опоре или к подвесу.
Вес возникает от того, что под действием силы тяжести тело стремится двигаться вниз, а опора препятствует этому движению. Именно поэтому тело давит на опору силой 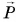 . В ответ на силу
. В ответ на силу 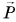 опора действует на тело силой реакции
опора действует на тело силой реакции 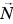 (рис. 165, а).
(рис. 165, а).
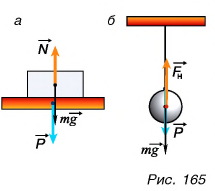
Как связаны между собой вес 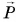 и сила тяжести mg?
и сила тяжести mg?
Проведем простой опыт. Положим тело массой т = 1 кг на чашу пружинных весов. Показания весов Р будут равны 9,8 И, т. е. Р = mg. Результат находится в полном согласии с законами Ньютона. По первому закону силы, действующие на покоящееся тело, компенсируют друг друга:

По третьему закону Ньютона

Значит, 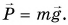
Но всегда ли вес численно равен силе тяжести?
Продолжим опыт в кабине лифта. Если лифт движется равномерно, то показания весов будут такими же, как в состоянии покоя. Вес 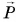 тела, движущегося равномерно и прямолинейно (как и покоящегося), равен силе тяжести mg.
тела, движущегося равномерно и прямолинейно (как и покоящегося), равен силе тяжести mg.
Пусть теперь кабина лифта движется с ускорением а. При ускорении, направленном вверх, результирующая сила тоже должна быть направлена вверх (рис. 166, а). Значит, N > mg. Но по третьему закону Ньютона модули сил N и Р равны. Следовательно, Р > mg, т. е. вес тела больше силы тяжести.
При ускорении кабины лифта, направленном вниз (рис. 1(56, б), вес тела уменьшается: Р < mg. Докажите это самостоятельно.
Если же кабина лифта будет двигаться с ускорением 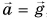 , т. е. свободно падать, то тело не будет действовать на опору, и показания весов станут равными нулю. Исчезнет не только давление тела на опору, но и давление одних частей тела рис. 166 на другие. Возникнет состояние невесомости.
, т. е. свободно падать, то тело не будет действовать на опору, и показания весов станут равными нулю. Исчезнет не только давление тела на опору, но и давление одних частей тела рис. 166 на другие. Возникнет состояние невесомости.
В состоянии невесомости находятся все свободно падающие тела.
Как вычислить вес ускоренно движущегося тела?
Для тела в ускоренно движущемся лифте по второму закону Ньютона 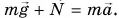 Значит, при
Значит, при 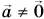 вместо равенства (1) получится:
вместо равенства (1) получится:

Учитывая, что 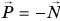 , находим:
, находим:

Формула (4) справедлива при любом направлении ускорения. Необходимо только помнить, что 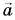 — ускорение движения тела (вместе с опорой) относительно инерциальной системы отсчета.
— ускорение движения тела (вместе с опорой) относительно инерциальной системы отсчета.
Числовое значение веса тела определяется модулем вектора 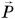 :
:

Изменение веса тела, обусловленное ускоренным движением, характеризуют перегрузкой Q. Ее определяют как отношение веса тела Р в рассматриваемых условиях к весу тела, покоящегося относительно Земли. Согласно формуле (5)
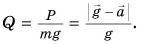
При 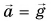 (т. е. при невесомости) Q = 0. В ракете, стартующей с Земли вертикально с ускорением
(т. е. при невесомости) Q = 0. В ракете, стартующей с Земли вертикально с ускорением 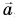 перегрузка
перегрузка 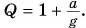

Большие перегрузки испытывают космонавты, тренируясь на центрифуге (рис. 167, а) и на участке разгона космического корабля ракетой-носителем.
По окончании работы двигателей и выходе за пределы атмосферы перегрузки сменяются состоянием невесомости. В состоянии длительной невесомости находится экипаж орбитальной станции (рис. 167, б).
Перегрузки и невесомость можно испытать, не отправляясь в полет. Перегрузки возникают при движении с разгоном, торможением, резкими поворотами (рис. 168). Состояние, близкое к невесомости, испытывает человек во время прыжка.

Главные выводы:
- Вес тела — это сила, с которой тело действует на опору (подвес) вследствие действия силы тяжести.
- Сила тяжести приложена к телу, а вес — к опоре или подвесу.
- Свободно падающие тела находятся в состоянии невесомости.
Пример №8
Человек массой 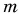 = 60 кг, находящийся в кабине лифта, движущейся вниз, давит на пол кабины силой
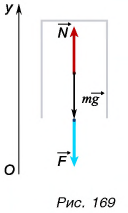
= 60 кг, находящийся в кабине лифта, движущейся вниз, давит на пол кабины силой 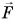 (рис. 169). Определите ускорение кабины лифта, если F = 690 Н. Примите
(рис. 169). Определите ускорение кабины лифта, если F = 690 Н. Примите 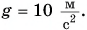

Решение
На человека в кабине лифта действуют сила тяжести 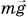 и сила реакции пола N.
и сила реакции пола N.
Но второму закону Ньютона
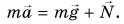
Но третьему закону Ньютона 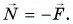 Тогда
Тогда 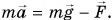 В проекции на ось Оу:
В проекции на ось Оу:
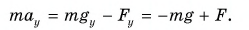
Отсюда
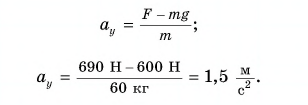
Так как 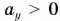 , ускорение кабины направлено вверх, хотя она опускается. Значит, кабина движется вниз замедленно (с торможением).
, ускорение кабины направлено вверх, хотя она опускается. Значит, кабина движется вниз замедленно (с торможением).
Ответ: 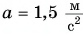 ускорение кабины лифта направлено вверх.
ускорение кабины лифта направлено вверх.
Законы динамики
Движение объектов окружающей среды вокруг нас подчиняется законам механики.
Впервые детально изучать причины изменения движения тела с помощью экспериментов начал Галилео Галилей (конец XVI века – начало XVII века). Он писал о причине изменения движения тела следующее.
Если на тело не воздействуют какие-либо тела, то тело сохраняет свое положение покоя или прямолинейное движение относительно земли.
Закон, установленный Галилеем, был первым шагом в открытии основных законов механики.
Впоследствии для открытия основных законов динамики Ньютоном были проведены простые опыты. Для их проведения не потребовалось никакого сложного оборудования. Самые большие трудности заключались в том, чтобы выделить самое важное из общего потока различных движений тел.
Динамика происходит от греческого слова «dynamis», что означает «сила». И когда мы видим, что какое-то тело движется, то мы можем наблюдать другие тела, которые на него действуют. Другое тело может притягивать, отталкивать или действовать на тела с большого расстояния (например, действие магнита на стальной шар). Если отпустить тело, поднятое на определенную высоту над землей, оно упадет вниз. Во всех этих экспериментах изменение скорости тела (то есть ускорение) всегда возникает от воздействия другого тела. Это выражение является наиболее важным заключением Ньютоновской механики.
Процесс взаимного действия тел друг на друга называется взаимодействием. То есть любое действие создает противодействие.
Но к такому заключению пришли не сразу. Великий мыслитель Аристотель пытался выяснить причину изменения движения тел. Он писал: «Если на тело не будет действовать толкающая сила, движущееся тело остановится». Аристотель считал, что состояние покоя относительно Земли это естественное состояние тела.
В те времена Земля считалась центром Вселенной и этим объясняли, что тело возвращается к своему естественному состоянию покоя, если не возникнет важной причины. Действительно, если закончится бензин в автомобиле, движущемся по ровной асфальтированной дороге, двигатель выключится. Автомобиль еще будет двигаться некоторое время и остановится. Такое же заключение можно применить к велосипеду и лодке на озере.
На основе наблюдений и выводов был сформулирован первый закон динамики.
Он выражается следующим образом:
Существуют такие системы, называемые инерциальными системами, в которых тело будет находиться в покое или продолжит прямолинейное равномерное движение, если на него не будет оказано внешнее воздействие.
Этот закон, с одной стороны, объясняет понятие «инерциальная система отсчета», а с другой – позволяет проверить, существуют ли такие системы. Первый закон механики ставит систему инерции на особое место.
Каждая точка вращающегося твердого тела двигается с ускорением. Ускорение любой части происходит под влиянием других частей тела. Иначе говоря, части, образующие твердое тело, не могут быть «свободными телами» и к ним не может быть применен первый закон Ньютона.
Таким образом, мы узнали, что причиной выхода тела из состояния покоя или прямолинейного равномерного движения является воздействие других тел. Взаимодействие тел характеризуется силой.
Согласно Ньютону, в механике количественная величина, которая является причиной получения ускорения в результате взаимодействия тел, называется силой.
Это качественное определение понятия силы. В механике этим определением вводятся два утверждения:
- ускорение тел происходит в результате действия сил;
- сила, дающая ускорение, возникает в результате действия других тел.
Понятие «сила» относится к двум телам. Сила является векторной величиной и имеет направление. Чтобы количественно определить силу, нужно ее измерить. Для этого она сравнивается с другой эталонной силой.
Если одновременное воздействие сил на тело не изменяет значение его скорости (т.е. не придает ему ускорения), то они равны по модулям и направлены противоположно.
Эксперименты показали, что ускорение, полученное телом, зависит не только от приложенной к нему силы, но и от свойства самого тела. Значит, необходимо уточнить это свойство. В механике оно характеризуется массой тела.
Вам известно из 7-го класса, что отношение приложенной к телу силы и получаемого телом ускорения является постоянной величиной.
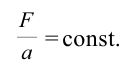
Физическая величина, характеризующая свойства тела и измеряемая отношением 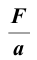 называется инертной массой.
называется инертной массой.
Масса определяет свойство инертности тела, т.е. характеризует его способность получать ускорение под воздействием приложенной силы.
С введением понятия массы второй закон динамики формулируется следующим образом:
Ускорение, полученное телом, прямо пропорционально приложенной силе и обратно пропорционально массе тела.

Этот закон является одним из фундаментальных законов. Ему подчиняется перемещение огромных небесных тел и движение мелких частиц песка, летящих по ветру.
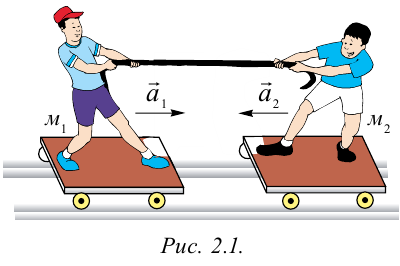
Как было сказано выше, взаимодействие возможно только между несколькими телами. Например, на рисунке 2.1, когда Алишер воздействовал на Баходира при помощи веревки, Баходир также обратно подействовал на Алишера. В результате как Алишер, так и Баходир получили ускорение.
Наблюдая подобные явления, можно сформулировать третий закон динамики.
Действие всегда вызывает противодействие. Силы действия и противодействия двух тел равны по величине, противоположны по направлению и направлены по прямой, проходящей через эти тела.

Поскольку силы действия и противодействия приложены к разным телам, они не могут уравновесить друг друга, т.е. взаимодействующие тела в результате воздействия этих сил получают разное ускорение:
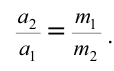
Пример №9
Под воздействием силы 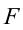 тело с массой
тело с массой 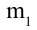 получает ускорение 2 м/c2 . Тело массой
получает ускорение 2 м/c2 . Тело массой 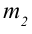 под воздействием этой же силы получает ускорение 5 м/c2.
под воздействием этой же силы получает ускорение 5 м/c2.
Если соединить эти тела, с каким ускорением они будут двигаться под воздействием этой силы?
Дано:
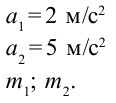
Найти:
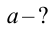
Формула:
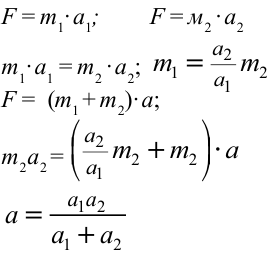
Решение:
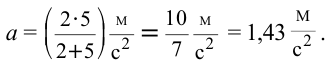
Ответ: 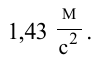
Карта изменения скорости движения тел в динамике:
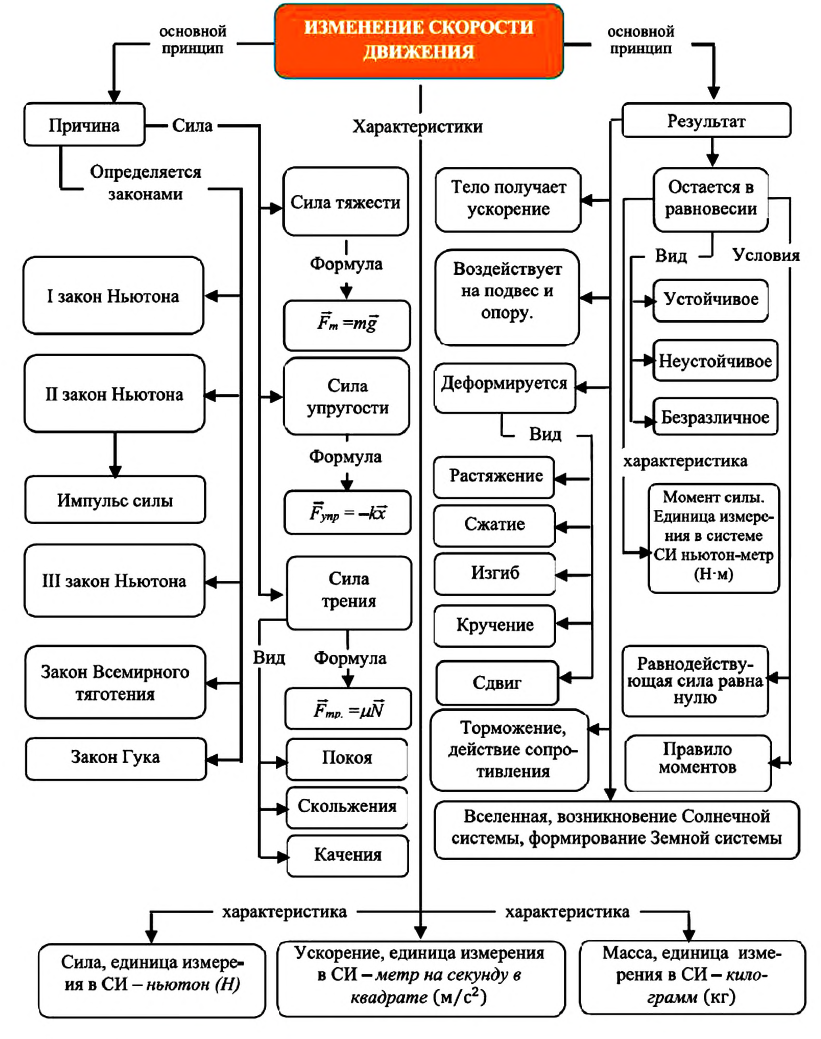
Основная задача динамики
Как вы уже знаете, причиной изменения скорости движения произвольного тела является взаимодействие его с другими телами.
Изучив учебный материал раздела "Кинематика", вы научились различать равномерное и равноускоренное движения, а также записать для них уравнения движения. Однако осталось невыясненным, по какой причине возникает равномерное или равноускоренное движение. Этот вопрос изучается в разделе механики, называемом динамикой.
Динамика (по-гречески dinamikos - "сильный", "мощный") - раздел механики, изучающий причины, определяющие характер движения, а также как эти причины изменяют характер движения.
Основная задача динамики — определить характер движения тела в соответствии с действующей на него силой, или наоборот, по характеру движения тела определить, какая сила действует на него.
Понятие "сила" является основополагающим в динамике. Сила - векторная физическая величина, характеризующая действие одного тела на другое и являющаяся мерой этого действия. Направление вектора силы совпадает с направлением действия тела, а его модуль выражает количественную меру действия.
Говоря об определенной силе, необходимо четко представить:
- на какое тело действует эта сила или к какому телу она приложена?
- к какой точке тела, имеющего определенные размеры, прикладывается эта сила?
- действие какого тела она характеризует?
- вдоль какой линии и куда направлена эта сила?
- чему равен её модуль?
При действии на тело нескольких сил их действие заменяется одной равнодействующей силой.
Равнодействующая сила - это векторная сумма всех сил, действующих на тело:
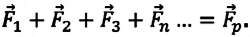
Например, если на материальную точку действуют две взаимноперпендикулярные силы 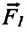 и
и 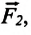 то они могут быть заменены вектором силы
то они могут быть заменены вектором силы 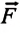 (а). Модуль этой силы:
(а). Модуль этой силы: 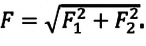
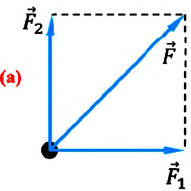
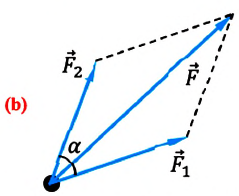
Если же на тело действуют две силы 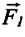 и
и 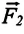 под произвольным углом
под произвольным углом 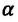 (b), то модуль равнодействующей силы определяется на основании теоремы косинусов:
(b), то модуль равнодействующей силы определяется на основании теоремы косинусов: 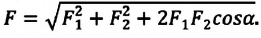 Ускорение приобретается телом под действием силы, поэтому в динамике понятие "ускорение" имеет более значимый смысл.
Ускорение приобретается телом под действием силы, поэтому в динамике понятие "ускорение" имеет более значимый смысл.
• Приобретение телом ускорения происходит в результате его взаимодействия с другими телами. Известно, что отношение ускорений двух взаимодействующих тел равно обратному отношению их масс:
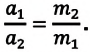
Это соотношение между ускорениями и массами взаимодействующих тел может быть использовано для определения масс тел. Но для этого сначала следует выбрать единицу массы - принять массу какого-либо тела за эталон. Затем тело, массу которого необходимо определить, привести во взаимодействие с телом, принятым за эталон. Далее, из соотношения между ускорениями и массами этих тел определяется неизвестная масса тела:
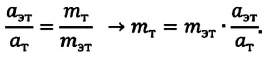
Законы динамики
Действие одного тела на другое описывается векторной физической величиной — силой. Сила характеризуется направлением, модулем и точкой приложения.
Действие силы является причиной изменения скорости тела. В отсутствие сил (взаимодействий) скорость тела не изменяется ни по модулю, ни по направлению.
Закон всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению их масс 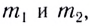 обратно пропорциональной квадрату расстояния r между ними и направленной по соединяющей их прямой:
обратно пропорциональной квадрату расстояния r между ними и направленной по соединяющей их прямой:
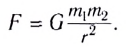
Кинематика, описывающая различные типы движения тел, не может ответить на вопрос о причинах возникновения, изменения и прекращения движения, поскольку для этого необходимо рассматривать закономерности механического взаимодействия тел. Закономерности механического взаимодействия тел являются предметом изучения следующего раздела механики — динамики.
Динамика — раздел механики, в котором изучается движение взаимодействующих материальных тел.
Термин «динамика» закрепился за этим разделом механики после выхода в свет в 1743 г. книги Ж. Л. Даламбера «Трактат по динамике».
Действие одного тела на другое в механике проявляется в деформации взаимодействующих тел и в изменении характера их движения.
Сила 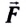 — векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел и полей.
— векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел и полей.
В результате действия силы (сил) тело приобретает ускорение и деформируется. Любая сила характеризуется модулем (абсолютной величиной), направлением и точкой приложения. Прямая линия, вдоль которой направлена сила, называется линией действия силы.
Единица силы в СИ — ньютон: 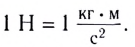
В качестве примеров различных сил можно привести силу всемирного тяготения 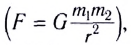 силу тяжести (F=mg), силу трения
силу тяжести (F=mg), силу трения 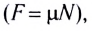 силу упругости
силу упругости 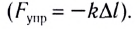
Для измерения модуля действующей силы с помощью пружинных весов или динамометра используется способность силы вызывать упругие деформации. О модуле силы можно также судить по ускорению, сообщаемому силой телу известной массы.
Опыт показывает, что при одновременном действии на тело нескольких сил 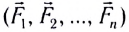 справедлив принцип суперпозиции сил, согласно которому их действие эквивалентно действию одной силы, называемой равнодействующей (результирующей)
справедлив принцип суперпозиции сил, согласно которому их действие эквивалентно действию одной силы, называемой равнодействующей (результирующей) 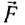 данных сил. Она является их векторной суммой:
данных сил. Она является их векторной суммой:
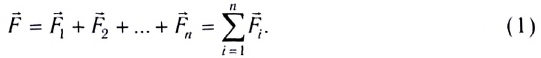
Например, равнодействующая двух сил 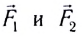 равна их векторной сумме (рис. 30):
равна их векторной сумме (рис. 30):
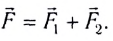
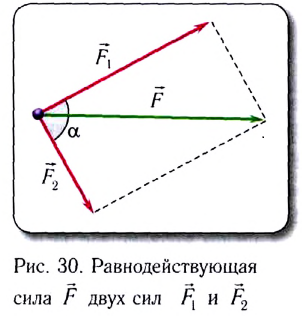
Модуль равнодействующей силы в данном случае вычисляется по формуле
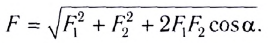
Силы 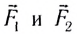 называются также составляющими силы
называются также составляющими силы 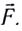
В основе классической динамики лежат три закона Ньютона, установленные в результате обобщения различных экспериментальных данных.
Первый закон Ньютона (закон инерции):
- существуют такие системы отсчета, называемые инерциальными, относительно которых тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или их воздействия скомпенсированы.
Отметим, что силы, действующие на рассматриваемое тело со стороны других тел, скомпенсированы, если их векторная сумма равна нулю 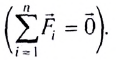
Тело, на которое не действуют силы со стороны других тел или их воздействие скомпенсировано, называется свободным. Подчеркнем, что движение свободного тела происходит по инерции до тех пор, пока не изменятся силы, действующие на него.
Термин «инерция» происходит от латинского слова iners — косность, бездеятельность.
Можно показать, что любая система отсчета, движущаяся относительно данной ИСО равномерно и прямолинейно, также является инерциальной.
Инерциальными системами отсчета в классической механике принято считать такие системы отсчета, в которых выполняется первый закон Ньютона — закон инерции. Время в классической механике носит абсолютный характер и не меняется при переходе от одной ИСО к другой.
Примерами ИСО являются, например, гелиоцентрическая, связанная с Солнцем, или геоцентрическая, связанная с Землей.
В классической механике справедлив принцип относительности Галилея, устанавливающий факт равноправности различных инерциальных систем отсчета:
во всех ИСО любые механические процессы протекают одинаково при одинаковых начальных условиях.
Иными словами, все ИСО равноправны между собой при изучении разнообразных механических процессов, и никакие эксперименты в замкнутой системе тел не позволят отличить одну инерциальную систему отсчета от другой. Так, никакими механическими экспериментами внутри лифта вы не сможете определить, покоится лифт или движется равномерно прямолинейно.
Аналитически первый закон Ньютона записывается в виде
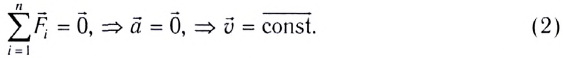
Система отсчета, относительно которой свободное тело не сохраняет скорость движения неизменной, называется неинерциальной.
При взаимодействии двух тел имеющее большую массу тело приобретает меньшее ускорение, т. е. оно более инертно:
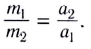
Инертность — свойство тела, характеризующее его способность к изменению скорости при взаимодействии с другими телами. Поскольку количественной мерой инертности является масса m тела, то ее в этом случае называют инертной массой.
С другой стороны, масса определяет также способность тел взаимодействовать с другими телами в соответствии с законом всемирного тяготения
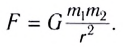
Такое взаимодействие называется также гравитационным (от латинского слова gravitas — тяжесть), и массу в этом случае называют гравитационной.
В современной физике с высокой точностью доказана тождественность значений гравитационной и инертной масс. Поэтому говорят просто о массе тела.
Измерение массы производят по измерению ускорения при взаимодействии исследуемого тела с эталоном: 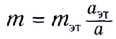 и взвешиванием тела на весах:
и взвешиванием тела на весах: 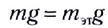 (g — ускорение свободного падения).
(g — ускорение свободного падения).
Таким образом, масса — это скалярная физическая величина, являющаяся количественной мерой инертных и гравитационных свойств тела.
Масса является аддитивной величиной, т. е. масса системы тел равна сумме масс отдельных тел, образующих систему: 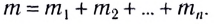
Единица массы — килограмм (1 кг) — является основной единицей в СИ.
ГВ качестве эталона килограмма установлена масса Международного прототипа килограмма, который представляет собой цилиндр диаметром и высотой 39 мм из платиноиридиевого сплава (90 % Pt и 10 % Iг) и хранится в Международном бюро мер и весов в Севре близ Парижа.
Второй и третий закон Ньютона
Импульс тела 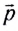 — векторная физическая величина, равная произведению массы тела и его скорости:
— векторная физическая величина, равная произведению массы тела и его скорости: 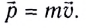
Эксперименты показывают, что действие силы приводит к изменению характера движения свободной материальной точки (тела) — в инерциальной системе отсчета у нее появляется ускорение, направление и модуль которого определяются вторым законом Ньютона.
Второй закон Ньютона (основной закон динамики):
- ускорение
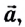 приобретаемое материальной точкой в любой ИСО под действием сил, прямо пропорционально равнодействующей
приобретаемое материальной точкой в любой ИСО под действием сил, прямо пропорционально равнодействующей 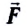 этих сил и обратно пропорционально массе m материальной точки:
этих сил и обратно пропорционально массе m материальной точки:

где 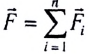 (рис. 31).
(рис. 31).
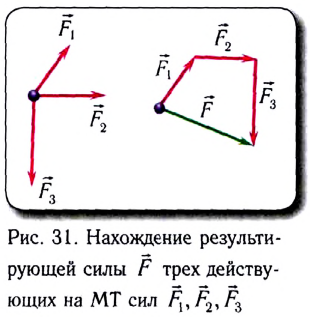
Таким образом, ускорение совпадает по направлению с результирующей силой: 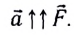
Основной закон динамики справедлив и для поступательного движения абсолютно твердого тела массой m, так как ускорение 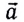 всех его точек одинаково.
всех его точек одинаково.
Отметим, что в случае непоступательного движения абсолютно твердого тела второй закон Ньютона определяет ускорение центра масс тела
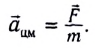
С учетом определения ускорения 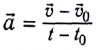 и импульса тела (МТ)
и импульса тела (МТ) 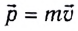 в случае действия постоянной результирующей силы
в случае действия постоянной результирующей силы 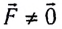 можно записать
можно записать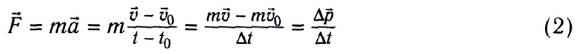
или
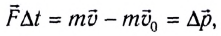
где 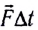 — импульс результирующей силы
— импульс результирующей силы 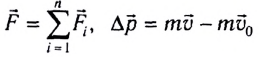 — изменение импульса тела (МТ).
— изменение импульса тела (МТ).
Подчеркнем, что импульс силы определяется как модулем, так и временем действия силы.
Термин «импульс» происходит от латинского слова impulsus — натиск, т. е. включает в себя представления как о величине, так и о продолжительности действия. Впервые этот термин еще до работ И. Ньютона был использован Дж. Валлисом в 1671 г.
Второй закон Ньютона в импульсной форме можно записать следующим образом:
- изменение импульса
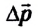 тела (МТ) относительно любой ИСО равно импульсу результирующей всех сил, подействовавших на него в течение промежутка времени
тела (МТ) относительно любой ИСО равно импульсу результирующей всех сил, подействовавших на него в течение промежутка времени 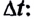

Таким образом, из второго закона Ньютона следует, что:
- а) приложенные к телу (МТ) силы являются причиной изменения его скорости;
- б) равнодействующая всех сил (независимо от их природы), приложенных к телу (МТ), определяет величину и направление его ускорения.
Второй закон Ньютона позволяет определить условие сохранения состояния покоя или равномерного движения тела (МТ) при действии на него других тел.
Таким условием является равенство нулю векторной суммы всех сил, действующих на тело (МТ):
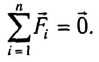
Второй закон Ньютона определяет уравнение движения материальной точки в векторной форме. Его используют для нахождения проекций сил и ускорений на оси прямоугольной декартовой системы координат.
Третий закон Ньютона устанавливает связь между силами, с которыми тела действуют друг на друга, и отражает факт взаимности механического действия (взаимодействия).
Третий закон Ньютона (закон действия и противодействия):
- при любых взаимодействиях двух тел на них действуют силы
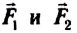 одинаковой природы со стороны одного тела на другое. Эти силы равны по модулю, противоположны по направлению и приложены к разным телам:
одинаковой природы со стороны одного тела на другое. Эти силы равны по модулю, противоположны по направлению и приложены к разным телам:
Здесь 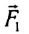 — сила, действующая на первое тело со стороны второго, a
— сила, действующая на первое тело со стороны второго, a 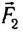 — на второе со стороны первого. Подчеркнем, что силы
— на второе со стороны первого. Подчеркнем, что силы 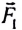 и
и 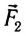 в случае взаимодействия материальных точек направлены вдоль соединяющей их прямой.
в случае взаимодействия материальных точек направлены вдоль соединяющей их прямой.
Так, при столкновении тележки действуют друг на друга с силами, равными по модулю и противоположными по направлению (рис. 32).
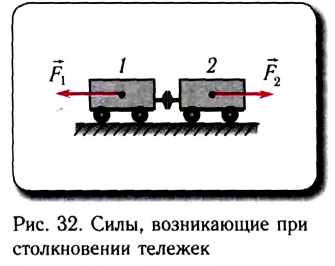
Из третьего закона Ньютона следует, что силы любой природы при различных взаимодействиях всегда возникают и исчезают парами.
Следует помнить, что рассматриваемые силы 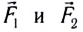 приложены к разным телам и по этой причине они не могут компенсировать друг друга, так как при вычислении равнодействующей складывают только силы, приложенные к одному телу.
приложены к разным телам и по этой причине они не могут компенсировать друг друга, так как при вычислении равнодействующей складывают только силы, приложенные к одному телу.
Примеры различных пар сил действия и противодействия приведены на рисунке 33.
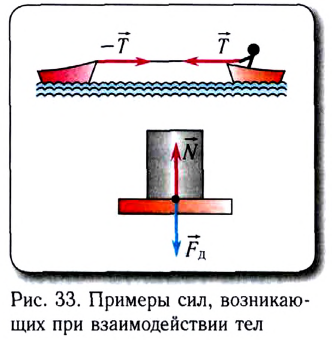
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |