Динамические реакции при вращении твердого тела вокруг неподвижной оси в теоретической механике

Формулы для реакций:

Твердое тело, имеющее две закрепленные точки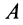

Приложив к точкам тела силы инерции, применим к телу следствия из принципа Даламбера для системы, считая, что тело разбито на 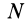частиц (малых), принимаемых за точки. Для этого следует приравнять нулю главный вектор и главный момент всех внешних сил и сил инерции точек тела. Имеем

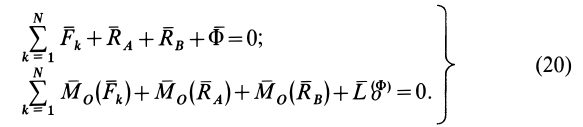
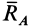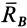Для определения из (20) сил реакций и необходимо выразить главный вектор сил инерции 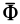и главный момент этих сил 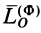через величины, характеризующие само тело и его вращение. Для главного вектора сил инерции используем выражение

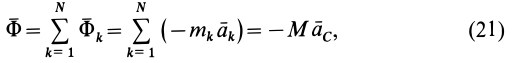
где 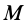— масса тела; 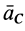— ускорение центра масс.

При вращении тела вокруг неподвижной оси ускорение любой точки тела вычисляется по формуле

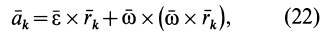
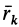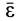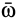где — радиус-вектор рассматриваемой точки;  и — соответственно векторы углового ускорения и угловой скорости тела, направленные по оси вращения. Для центра масс в (22) вектор 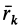следует заменить радиусом-вектором центра масс .

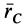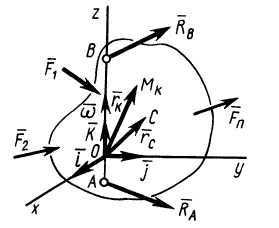
Рис. 86

Векторное произведение двух векторов выражается определителем, в первой строке которого расположены единичные векторы 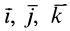, направленные вдоль осей координат, а в двух других строках — проекции на оси координат векторов сомножителей. Определитель можно разложить по элементам первой строки. Получим

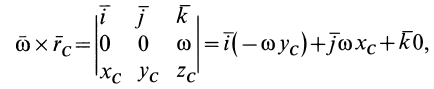
так как 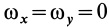 и 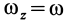. Здесь 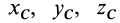— координаты центра масс. Используя полученные величины для ускорения центра масс 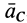, имеем

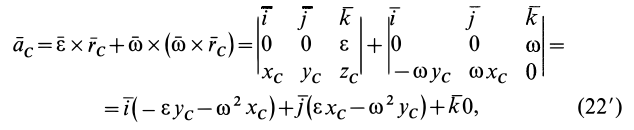
так как , .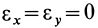

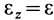Из (21) с учетом (22') для проекций главного вектора сил инерции на оси координат получаем выражения

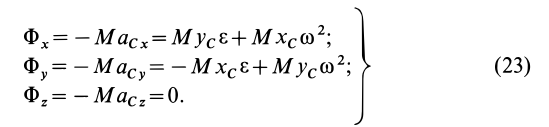
Формулы (23) можно применять не только для главного вектора сил инерции, но и для силы инерции отдельной точки тела. Для этого следует массу тела 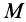в них заменить массой точки 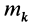, а координаты 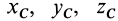центра масс — координатами 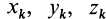точки. Так, для силы инерции 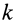-й точки 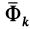, согласно (23), имеем

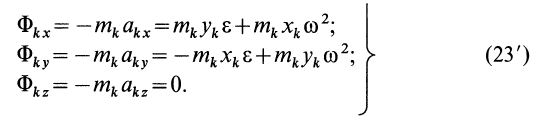
Проекции главного момента сил инерции относительно точки на оси вращения 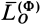на оси координат вычисляем по формулам для моментов сил относительно этих осей. Используя (23') и вынося 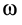и 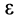за знаки сумм, получаем:

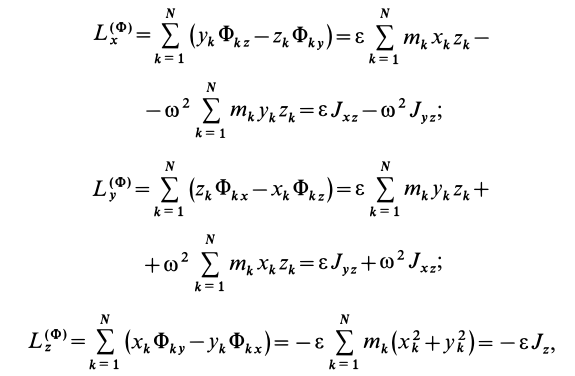
где 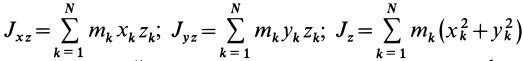—центробежные и осевой моменты инерции. Получены формулы для вычисления проекций главного момента сил инерции  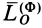на координатные оси:

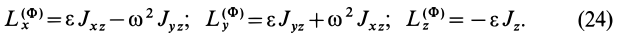
При выводе формул (23) и (24) для проекций главного вектора и главного момента сил инерции на оси координат не делалось никаких предположений относительно этих осей. Они могут быть как неподвижными осями, относительно которых рассматривается вращение тела, так и подвижными осями, скрепленными с вращающимся телом. Поэтому эти формулы можно применять как для неподвижных осей координат, так и для осей координат, вращающихся вместе с телом.

Из (20) в проекциях на координатные оси с учетом (23) и (24) получаем следующую систему уравнений для определения проекций полных реакци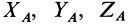й и :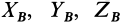

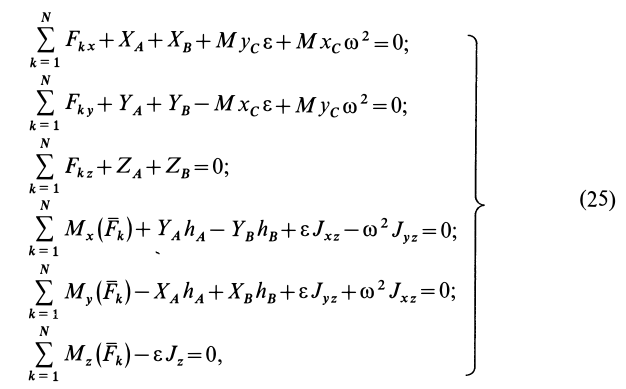
так как

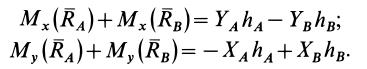
В последнее уравнение системы (25) не входят силы реакций закрепленных точек. Это уравнение является уравнением вращения твердого тела вокруг неподвижной оси 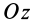. Из него по заданным силам определяется угловое ускорение 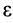, если известен момент инерции тела относительно оси вращения. По угловому ускорению интегрированием определяется угловая скорость, если известно ее значение в начальный момент. Для определения шести неизвестных проекций сил реакций остается пять уравнений. Система уравнений (25) не позволяет определить каждую из неизвестных 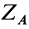и 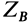. Из третьего уравнения системы можно определить только неизвестных. Для того чтобы из этой системы определить все неизвестные, необходимо закрепить тело в точках 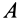и 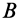так, чтобы неизвестных проекций сил реакций в них было не более пяти. Этого можно достигнуть, например, поместив в точке 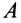подпятник, а в точке 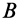— подшипник (рис. 87). Для таких опор оси тела 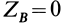и все оставшиеся неизвестные могут быть определены из системы уравнений (25).

Разложим полные реакци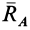и и 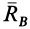на статические и динамические составляющие:

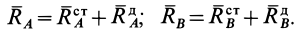
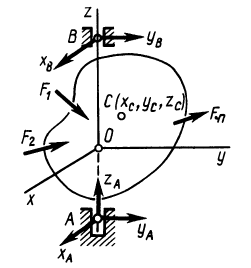
Рис. 87

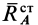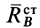Статическими реакциями  и называют части полных реакций, которые статически уравновешивают приложенные внешние силы. Уравнение для их определения получим из первых пяти уравнений системы (25), положив в них 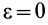и 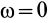. Имеем

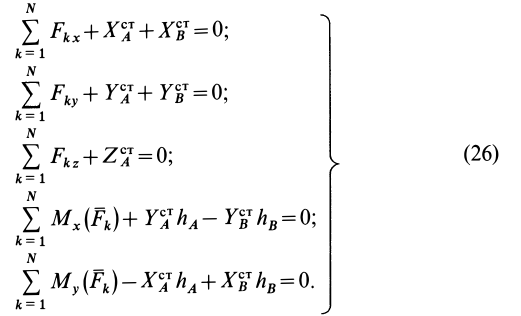
В векторной форме (26) принимают вид

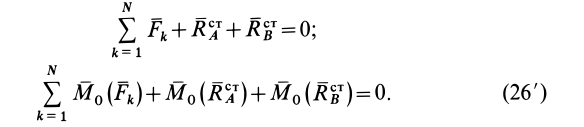
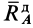Это известные из статики уравнения равновесия для сил, приложенных к твердому телу, имеющему неподвижную ось вращения. Но под действием приложенных внешних сил тело может вращаться вокруг неподвижной оси . От вращения у точек тела возникнут силы инерции. Части полных реакций и 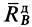, которые уравновешивают силы инерции точек тела, называют динамическими реакциями.

Уравнения для определения динамических реакций получим из первых пяти уравнений системы (25), если учтем, что приложенные внешние силы уравновешены статическими реакциями. Получим

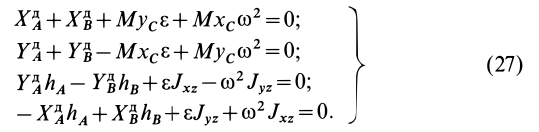
В векторной форме (27) принимают вид

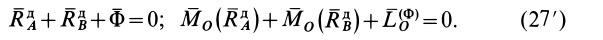
Составляющих динамических реакций опор в направлении оси вращения 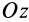не возникает, так как у точек тела нет составляющих сил инерции в этом направлении. В неподвижных точках тела имеются только поперечные по отношению к оси вращения составляющие динамических реакций. Это справедливо при любом закреплении точек 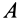и 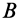, позволяющем телу вращаться вокруг оси, проходящей через эти точки. Из системы уравнений (27) определяются все проекции динамических реакций на оси координат.

Статическая уравновешенность:

Тело, имеющее неподвижную ось вращения, называют статически уравновешенным, если центр масс этого тела находится на оси вращения. Для статически уравновешенного тела с осью вращения 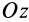координаты центра масс тела 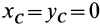. Из первых двух уравнений системы (27) в этом случае следует:

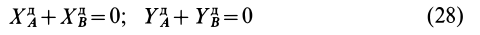
или

Динамические реакции для статически уравновешенного тела образуют пару сил. Пара сил может уравновешиваться только парой сил. Следовательно, силы инерции точек тела, уравновешивающие динамические реакции, в этом случае тоже приводятся к одной паре сил.

Используя (28), из двух последних уравнений системы (27) получим:

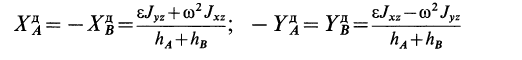
и

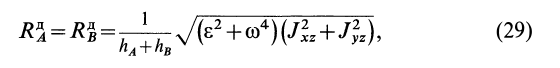
где

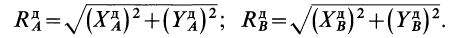
Из (29) следует, что динамические реакции зависят не только от углового ускорения, но и от угловой скорости, т. е. они возникают даже при вращении тела по инерции с постоянной угловой скоростью. Динамические реакции пропорциональны квадрату угловой скорости как в частном случае статической уравновешенности, так и в общем случае и при вращении тела с большой угловой скоростью могут достигать довольно значительных величин.

Формулы (23) и (24) справедливы как для неподвижных, так и подвижных осей координат. Этим же свойством обладают и формулы (27). Поэтому динамические реакции как в частном случае статически уравновешенного тела, так и в общем случае, когда центр масс не находится на оси вращения, можно считать вращающимися вместе с подвижными осями координат, если угловая скорость постоянна. Опоры оси вращения тела будут испытывать действие циклически изменяющихся динамических давлений, что может привести к их усталостному разрушению или разрушению от вибраций, если собственная круговая частота мест их закрепления совпадает или близка к угловой скорости вращения тела.

Динамическая уравновешенность:

Динамической уравновешенностью называется случай обращения в нуль динамических реакций. Динамические реакции обратятся в нуль, как следует из (29), если равны нулю центробежные моменты инерци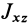и и 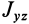, т. е. дополнительно к статической уравновешенности ось вращения 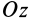должна быть главной осью инерции для любой точки  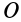этой оси. Так как центр масс в этом случае расположен на этой оси, то ось вращения при динамической уравновешенности является главной центральной осью инерции. При вращении тела вокруг главной центральной оси инерции динамические реакции обращаются в нуль. Следовательно, силы инерции точек тела, создающие динамические реакции, в этом случае образуют равновесную систему сил. Главный вектор и момент сил инерци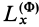и  и 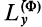равны нулю. Момент сил инерции 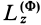при этом может быть отличным от нуля.

Главную центральную ось инерции называют свободной осью вращения — свободной от динамических реакций опор. При вращении тела вокруг свободной оси вращения могут возникнуть только статические реакции. Если тяжелое тело вращается по инерции с постоянной угловой скоростью вокруг свободной оси вращения, то статические реакции должны уравновесить только силу тяготения тела. При специальном дополнительном движении тела кроме вращения его вокруг оси с постоянной угловой скоростью может возникнуть положение, при котором силы инерции точек тела приведутся к равнодействующей силе, уравновешивающей силу тяготения. В этом случае статические реакции тоже обратятся в нуль и подшипник и подпятник для крепления оси вращения окажутся ненужными. Такое положение имеет место при вращении земного шара вокруг оси и его дополнительном движении по орбите вокруг Солнца. То же имеет место для других планет Солнечной системы, а также при движении Луны вокруг Земли и при движении естественных и искусственных спутников планет.

Для того чтобы сделать ось вращения тела свободной осью вращения, в технике осуществляют его балансировку на специальных балансировочных установках. При этом прибегают иногда к высверливанию в теле отверстий и при необходимости заполняют их более тяжелым металлом, например свинцом.

Основные виды неуравновешенностей:

Неуравновешенности тоже можно разделить на статические и динамические.

Если ось вращения является главной осью инерции хотя бы для одной точки на оси 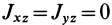, а центр масс не находится на оси вращения, то из (27') следует, что динамические реакции взаимно параллельны. Этот случай можно назвать статической неуравновешенностью.

Если центр масс находится на оси вращения, а ось вращения не является главной ни для одной точки этой оси, то имеем случай статической уравновешенности. Его также можно назвать динамической неуравновешенностью. Динамические реакции в этом случае образуют пару сил.

Общий случай неуравновешенности, когда и центр масс не находится на оси вращения, и нет точки на этой оси, для которой она была бы главной осью инерции, можно считать наложением двух неуравновешенностей: статической и динамической. Динамические реакции получаются при этом сложением реакций от двух указанных неуравновешенностей.

Пример 1. Однородная прямоугольная пластина длиной 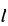, шириной 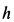и силой тяжести 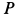может вращаться без трения вокруг горизонтальной оси 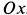, пересекающей вертикальную ось вращения 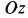в точке 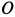(рис. 88). Пластина наклонена к оси вращения  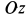на угол 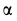и удерживается под этим углом пружиной, которая перпендикулярна оси вращения и имеет жесткость 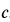. Пружина не деформирована при .

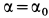Определить угол 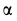, считая его малым, и полные реакции подпятника 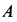и подшипника 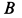при вращении пластины вокруг вертикальной оси с постоянной угловой скоростью 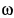, если .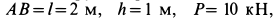

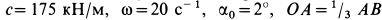Решение. Применим к пластине следствие из принципа Даламбера, приравняв нулю сумму моментов внешних сил и сил инерции относительно оси 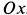. Действие пружины на пластину заменим силой упругости 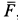, а действие подшипника в точке 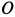— силами реакци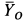й  и 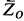 (рис. 89). В точке 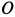приложим также главный вектор сил инерции 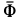, параллельный оси 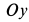(ускорение центра масс 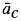параллельно этой оси), и главный момент этих сил 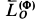. Имеем

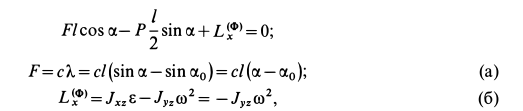
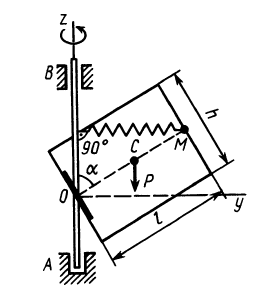
Рис. 88

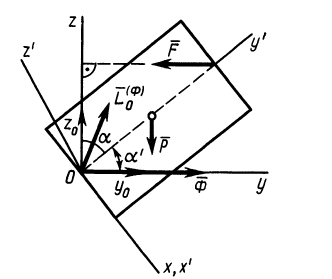
Рис. 89

так как

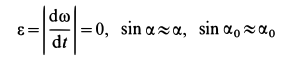
для малых углов 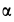и 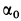. Подставляя эти значения в (а), получим следующее уравнение для определения :

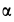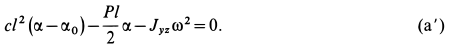
Центробежный момент инерции 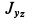вычислим по формуле (35') (см. § 9 гл. 3). Имеем

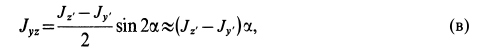
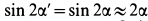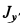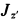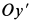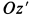так как sin , где и — моменты инерции относительно главных осей инерции и . Ось 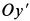 является осью симметрии пластины, и поэтому она является главной осью инерции для всех точек этой оси. Ось  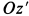перпендикулярна пластине, плоскость которой служит для нее плоскостью симметрии. Такая ось тоже является главной осью инерции для точки 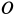, расположенной в этой плоскости.

Для главных моментов инерции пластины, согласно формуле (13) (см. § 4 гл. 3), соответственно имеем

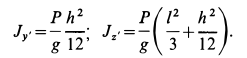
Подставляя эти величины в (в), получим

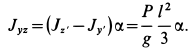
После этого для 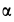из (а') имеем

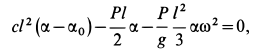
или

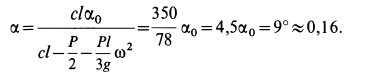
Для определения полных реакций подпятника 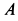и подшипника 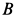рассмотрим систему тел, состоящую из пластины, пружины и стержня 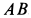, заменив действия подпятника и подшипника силами реакций, разложенными на составляющие, параллельные осям координат (рис. 90).

• Заказать решение задач по теоретической механике

По формулам (25) имеем

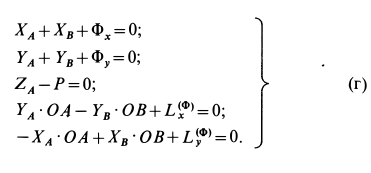
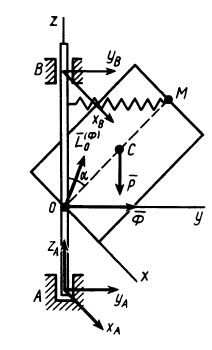
Рис. 90

Проекции главного вектора и главного момента сил инерции вычисляем по формулам (23) и (24); учитывая, что 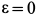, получаем

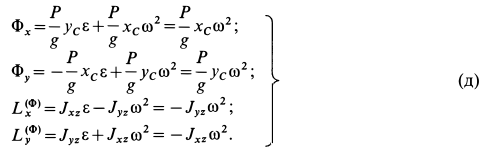
Ось 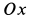перпендикулярна плоскости симметрии пластины, проходящей через 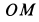перпендикулярно пластине. Следовательно, она является главной осью инерции для точки 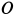, поэтому 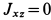. Кроме того, в рассматриваемом случае

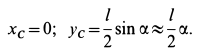
С учетом этого из (г) получаем следующую систему уравнений:

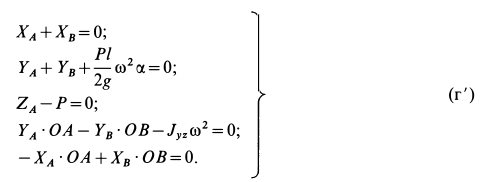
Из первого и последнего уравнений этой системы следует

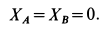
Третье уравнение дает

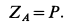
Из второго и четвертого уравнений (г) получаем

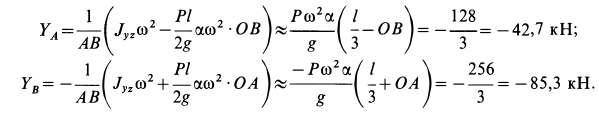
Пример 2. Однородный круглый цилиндр силой тяжести 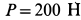, радиусом 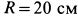, длиной 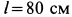с помощью вала 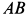вращается вокруг вертикальной оси с постоянной угловой скоростью 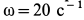(рис.91). Ось вращения касается поверхности цилиндра посередине образующей в точке 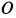так, что отрезок 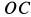, соединяющий точку касания с центром масс цилиндра, перпендикулярен оси вращения. Продольная ось цилиндра наклонена к вертикали на угол .

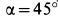Определить динамические реакции подшипника 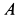и подпятника 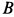, если 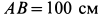, 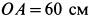. Массой вала 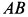пренебречь.

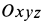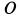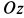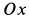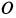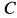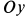Решение. Выберем правую систему осей координат , скрепленных с движущимся цилиндром и началом координат в точке . Ось направим по оси вращения; ось — по линии, соединяющей точку с центром масс , ось направим перпендикулярно 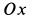и .

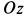Динамические реакции вместе с силами инерции системы образуют равновесную систему сил, т. е. удовлетворяют условиям равновесия для сил

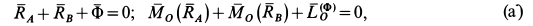
где 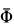— главный вектор сил инерции;  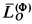— главный момент сил инерции относительно точки , выбранной за центр приведения сил инерции. Главный вектор сил инерции при вращении цилиндра вокруг неподвижной оси вычисляется по формулам

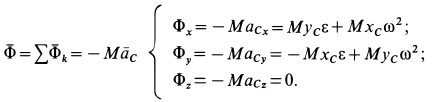
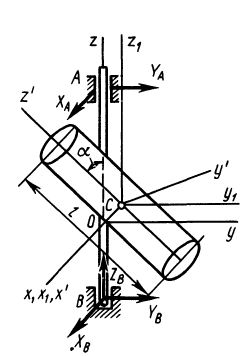
Рис. 91

Для главного момента сил инерции относительно точки на оси вращения справедливы формулы

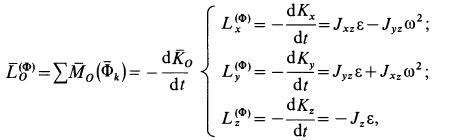
здесь 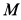— масса цилиндра;  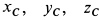— координаты центра масс. При сделанном выборе осей координат 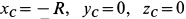. Кроме того, так как 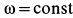, то угловое ускорение 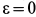. Еще одно упрощение связано с тем, что ось 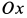является главной осью инерции для точки 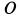, так как эта точка находится на главной центральной оси инерции 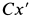. Поэтому .

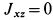С учетом упрощений спроецируем векторные уравнения (а) на оси координат. Получим следующие пять уравнений для определения динамических реакций:

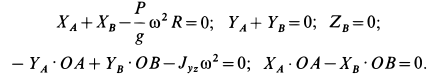
Из второго и четвертого уравнений этой системы определяем проекции динамических реакци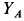й и 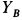. Имеем

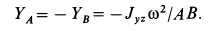
Из первого и пятого уравнений соответственно получаем

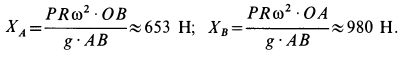
Для полного решения задачи необходимо вычислить центробежный момент инерции .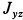

Центробежные моменты инерции обычно вычисляются через главные центральные осевые моменты инерции. Получим необходимую формулу.

Выберем в точке 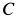систему координат 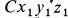, оси которой параллельны осям системы координат 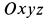. Координаты любой точки цилиндра относительно этих двух систем осей координат связаны между собой формулами параллельного переноса в направлении оси  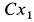на величину 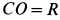; поэтому

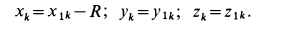
Так как

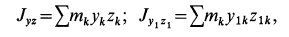
то

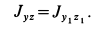
Для вычисления центробежного момента инерции 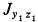в качестве вспомогательных осей координат возьмем главные центральные оси инерции цилиндра 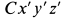(оси его симметрии). Систему осей координат 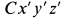можно получить из системы 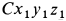, поворачивая ее на угол а вокруг оси 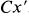. Формулы преобразования координат любой точки тела при повороте осей (рис. 92) можно выразить в форме

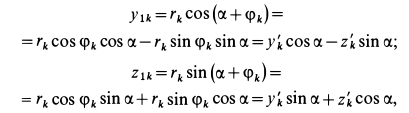
так как

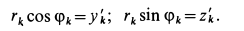
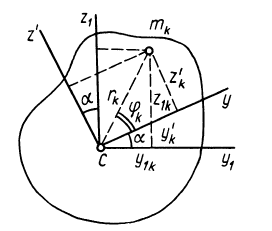
Рис. 92

Используя эти формулы, имеем

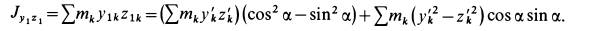
В рассматриваемом случае

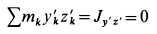
как центробежный момент инерции относительно главных осей инерции , .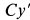

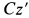Прибавляя в выражении для 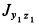   величину

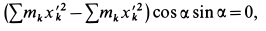
получаем

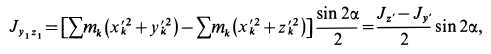
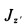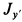где и — моменты инерции относительно главных центральных осей инерци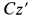и и 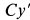соответственно. Они для цилиндра определяются по формулам

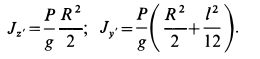
Итак, для искомого центробежного момента инерции имеем

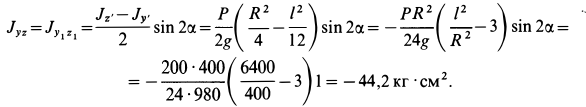
После этого

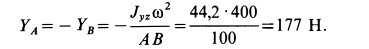
Таким образом определены проекции динамических реакций на оси координат, т. е. поставленная задача решена.