Дифференциальные уравнения движения материальной точки в теоретической механике

Содержание:

Дифференциальные уравнения движения материальной точки:

Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.

Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей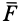

Из кинематики точки известно, что ускорение 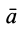выражается через радиус-вектор 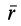(рис. 3):

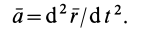
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид

Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.

В декартовой системе координат в общем случае

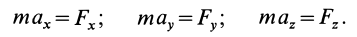
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:  

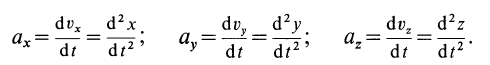
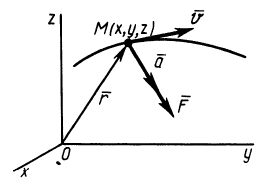
Рис. 3

Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид

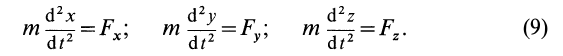
Частные случаи дифференциального уравнения движения материальной точки

Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 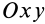, имеем

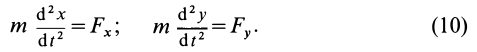
Так как , то, следовательно, . В случае движения точки по прямой линии, направив по ней координатную ось 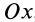, получим одно дифференциальное уравнение прямолинейного движения точки

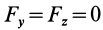Так как при движении , то, следовательно, . Для естественных подвижных осей координат (рис. 4), проецируя обе части (7) на эти оси, получаем:

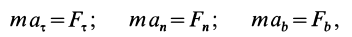
где 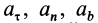и 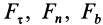— соответственно проекции ускорения и равнодействующей силы на касательную, главную нормаль и бинормаль к траектории в рассматриваемом положении движущейся точки. Учитывая, что

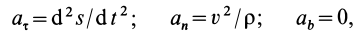
где 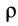 — радиус кривизны траектории, дифференциальные уравнения движения точки в проекциях на естественные оси имеют вид

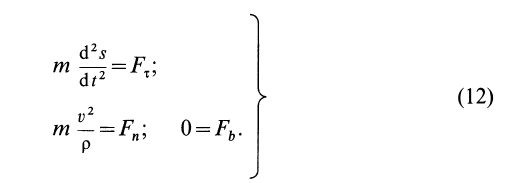
Второе уравнение из (12) можно преобразовать:

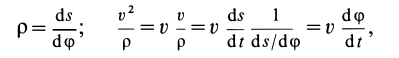
где 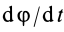— угловая скорость вращения касательной к траектории движущейся точки и, следовательно,  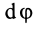— угол смежности между касательными в двух бесконечно близких точках.

Дифференциальные уравнения (12) можно представить в виде

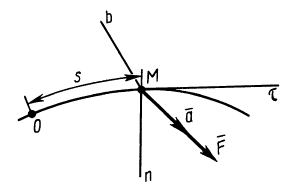
Рис. 4

Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 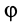 будет углом между касательной к траектории и любой осью, лежащей в плоскости траектории.

Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.

Дифференциальные уравнения относительного движения точки

Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения

Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):

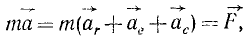
откуда 

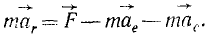
Векторную величину

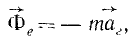                    (153)

имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.

Векторную величину

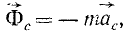                     (154)

равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.

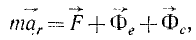                     (155^/)

или в проекциях на оси координат:

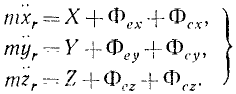                     (155)

Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.

Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.

Пример решения задачи №1

Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.

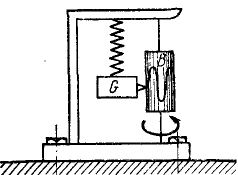
Рис. 171

Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х' груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна

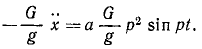
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:

x' + k²χ' = ар² sin pt.

где 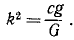 Пренебрегая свободными колебаниями груза, напишем уравнение (149') установившегося вынужденного колебания груза:

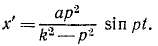
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.

Ответ.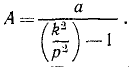  

• Заказать решение задач по теоретической механике

Пример решения задачи №2

Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 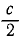каждая. Принимая ползун за точку массы т и пренебрегая трением, определить зависимость периода τ его колебаний в относительном движении по хорде от угловой скорости ω диска.

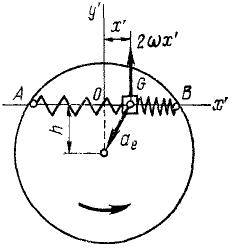
Рис. 172

Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox' но хорде.

Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х', то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х' и направлена к точке О. Следовательно, на ползун действует активная сила

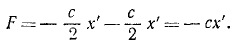
Кроме активной силы, надо учесть действие кориолисовых сил: Φ_e—переносной и Φ_c-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 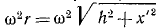 и направлена против переносного ускорения, т. е. от центра C диска. Чтобы определить проекцию этой силы на Ox', надо ее модуль умножить на направляющий косинус, который при OG = х' равен .

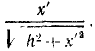Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx' и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox' равна нулю.

При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:

mх' = — cx' + mω²x'= — (с—mω²)x'.

Это уравнение выражает гармоническое колебание с периодом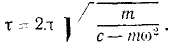 

Ответ. 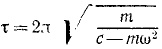  и не зависит от положения хорды.

Пример решения задачи №3

Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.

Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.

Поворотная сила ползуна Φ_с=2mωx' переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у', если точка G движется в сторону отрицательных значений х', т. е, если х' < 0, и, наоборот, в сторону отрицательных у', если х' положительно. А так как сила трения направлена всегда против относительной скорости, то силу трения, обусловленную давлением Φ_с, мы вполне определим по величине и по знаку выражением

— f2mωx'.

Нормальная составляющая переносной силы инерции ползуна постоянна по величине и всегда направлена в сторону положительных у'. Чтобы ее определить, надо 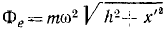умножить на 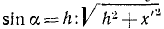. Тогда получим mω²h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у', а потому в суммарном давлении обе кориолисовы силы складываются при х' < 0 и вычитаются при х' > 0, и дифференциальное уравнение относительного движения точки имеет вид

mх' =— (с—mω²) x' — fm (2ωx' ± ω2h),

причем знак второго слагаемого в скобках надо брать положительным при х' < 0 и отрицательным при х' > 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.