Дифференциальное исчисление функций одной переменной с примерами решения

Содержание:

Понятие производной является одним из основных понятий дифференциального исчисления, производная используется при исследовании процессов, в том числе и экономических, описываемых функциями. При исследовании приращеиия зависимой величины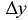

Некоторые задачи, приводящие к понятию производной:

Построение касательной к графику функции

Рассмотрим функцию f, определенную на промежутке X со значениями у = f(x). Графиком функции y = f(x) в системе координат XOY является непрерывная кривая L. Пусть 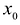-внутренняя точка промежутка X, 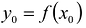- значение функции f в точке 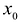. Возьмем на кривой L некоторую фиксированную точку 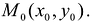. Если точка 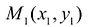тоже принадлежит кривой, то прямая 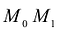называется секущей. Если перемещать 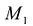вдоль кривой L так, чтобы 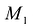, стремилась к совпадению с 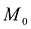, то секущая также будет менять свое положение в зависимости от положения 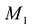. Предельное положение секущей (если оно существует) при 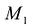-> 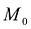называется касательной к кривой L в точке .

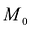Угловой коэффициент секущей tga равен:

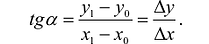
Величину 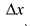называют приращением аргумента x. Величину 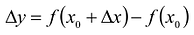называют приращением функции в точке 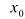, которое вызвано приращением аргумента. Поскольку точка 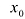фиксирована, то 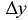является функцией от Ах, следовательно, и tga зависит только от .

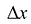Так как 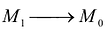, равносильно 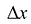—>0, то угловой коэффициент касательной можно получить предельным переходом при 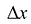-> 0 (если этот предел существует), т.е.:

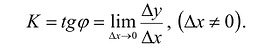
Предел относительного приращения 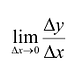называется производной функции y = f(x). Производную функции в точке 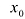обозначают одним из символов: 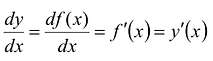и др.

Значение производной непрерывной функции в точке 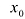равно тангенсу угла наклона касательной к графику этой функции в точке .

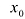Экономический смысл производной

Отношение 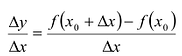представляет собой среднюю скорость изменения функции f на промежутке с концами 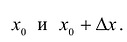Величина 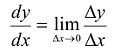- это мгновенная скорость изменения функции f в точке 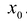. Например, если у = f(x) - перемещение точки по оси Ох за время х, то 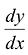- скорость движения точки. Если функция у = f{x) описывает количество продукции, производимой предприятием за время л-, то 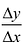- это средняя производительность за промежуток времени [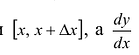- это производительность в момент времени x. Если функция у = f(x) описывает закон изменения капитала в зависимости от времени, то 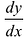- скорость накопления капитала.

Эластичность функции

Если функция y = f(x) получает приращение 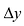при приращении аргумента на 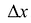, то 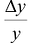называется относительным приращением функции, а 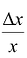- относительным приращением аргумента.

Эластичностью функции называется предел отношения относительного приращения функции к относительному приращению аргумента, если приращение аргумента стремится к нулю, т.е.:

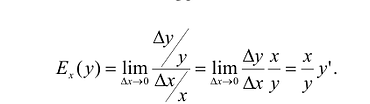
Эластичность функции дает приближенный процентный прирост функции при приращении аргумента на 1%.

Дифференцируемость функции

Eсли для точки 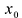существует число А такое, что приращение функции 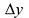представимо в виде 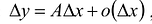, то говорят, что функция у = f(х) дифференцируема в точке 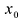. Число А является производной функции f в точке :

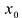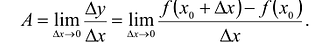
Таким образом, дифференцируемость функции в точке 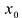означает, что в этой точке существует производная функции.

Итак, если f дифференцируема в точке х, то: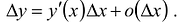

Величину 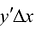называют дифференциалом функции в точке Л' и обозначают обычно символами: 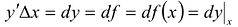и др.

Если функция у = f(x) дифференцируема в точке 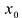, то эта функция непрерывна в точке 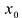. Обратное утверждение неверно.

Правила дифференцирования

Будем считать, что функции u, v, w дифференцируемы, т.е. имеют производные 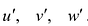. Тогда:

1. Функция u + v дифференцируема и
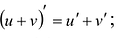
2. Если с - постоянная, то функция си дифференцируема и
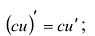
3. Из 1 и 2 следует, что
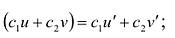
4. Функция uv дифференцируема и
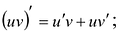
5. Из 4 следует, что
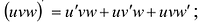
6. Если 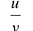определена и дифференцируема, то .

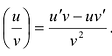Таблица производных

Основные элементарные функции дифференцируемы всюду, где они определены. Производные этих функций могут быть вычислены по определению, т.е. по формуле:

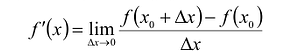
и с помощью правил дифференцирования.

Полученные значения производных основных элементарных функций приведем в таблице.

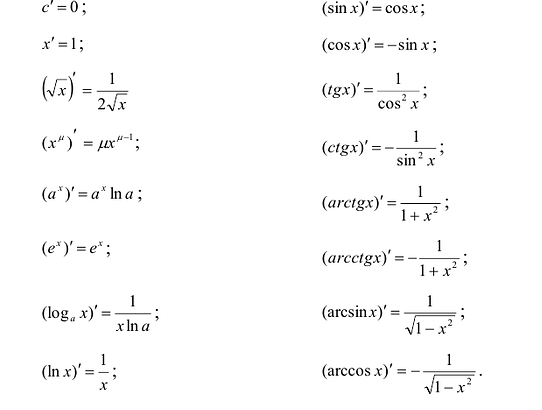
Использование таблицы производных и правил дифференцирования позволяет вычислять производные арифметических комбинаций основных элементарных функций.

Производная сложной функции

Пусть у = f(x) и x = 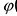(t). Тогда можно определить сложную функцию у = f((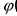(t)). Если функция 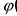дифференцируема в точке 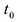, а функция f дифференцируема в точке 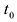то сложная функция 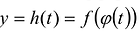дифференцируема в точке 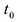, и ее производная может быть вычислена по правилу цепочки:

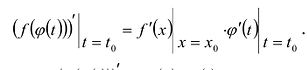
Или более кратко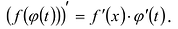

Правило можно записать также в виде: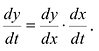

Пример:

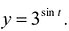. Вычислить у'.

Обозначим 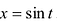. Тогда .у =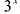

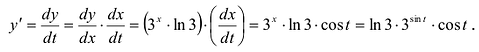
Пример:

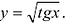Вычислить у'.

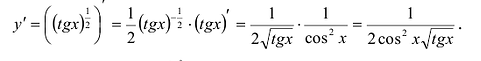
Пример:

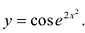Вычислить у'.

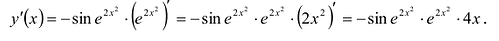
Производная обратной функции

Пусть функция у = f(х) задана на множестве X, a У - множество ее значений. Тогда каждому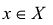 ставится в соответствие единственное значение 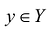. С другой стороны, каждому 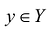будет соответствовать одно или несколько значений .

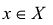В случае, когда отображение у = f(x) является биективным, т.е. каждому значению у е У соответствует только одно значение 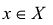, для которого f(x) = у, на множестве У можно определить функцию 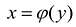, множеством значений которой является X, которая будет называться обратной по отношению к функции f(x) = у. Функции f и 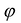называются взаимообратными.

Пусть функция у = f(x) удовлетворяет условиям существования обратной функции и в точке 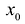имеет конечную производную 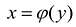. Тогда обратная функция 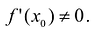в точке 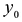также имеет конечную производную, равную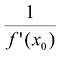

Дифференциал

Дифференцируемость функции у = f(x) в точке х означает, что ее приращение представимо в виде:

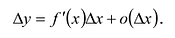
Величина 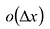при малых 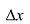мала по сравнению с величиной 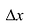. Поэтому 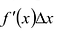представляет собой главную часть приращения 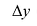, называемую дифференциалом функции в точке x. Дифференциал функции у = f(x) обозначают обычно символами: 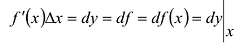и др.

Если x - независимая переменная, то 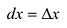и поэтому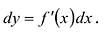

Вычисление дифференциалов проводят по правилам 1 - 6 дифференцирования с заменой символа ' (штрих) на символ d. Например:

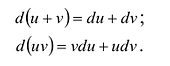
Таким образом, приращение функции 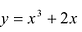в точке x = 1 при малых значениях 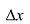приблизительно в пять раз больше, чем 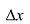, а приращение функции в точке х = 2 приблизительно в 14 раз больше, чем .

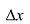Приближенные вычисления

Тот факт, что дифференциал функции является главной частью приращения функции, используют при различных приближенных вычислениях. При этом заменяют приращения функции 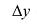ее приближенным значением 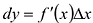. Таким образом: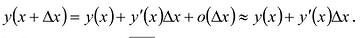

Пример:

Вычислить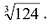

Рассмотрим функцию 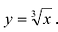. Заметим, что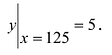

Возьмем 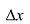= -1. Тогда по формуле (2):

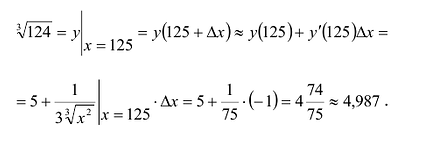
Свойства дифференцируемых функций

Теорема Ферма. Если функция у = f(x) дифференцируема в точке а у т.е. существует 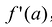, и всюду в некоторой окрестности этой точки f(x)< f(a) (f(x)>f(a)), т.е. f(a) является наибольшим (наименьшим) значением функции в этой окрестности, то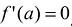

Теорема Ролля. Если функция у = f(х) непрерывна на отрезке 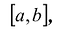, дифференцируема на интервале 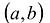и f(b) = f(a), то в некоторой точке интервала 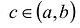ее производная равна нулю.

Геометрический смысл теоремы Ролля заключается в том, что в 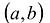найдется точка, в которой касательная к кривой будет горизонтальна.

Теорема Лагранжа. Если функция у = f(x) непрерывна на отрезке [a,b], дифференцируема на интервале 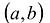, то найдется точка 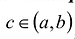для которой f(b) - f (а) = f' (c)(b - а).

Следствие. Теорема Лагранжа является обобщением теоремы Ролля для случая f{b) = f(a). Тогда f' (c) = 0.

Теорема Koши. Если функции f(x) и g(x) определены и непрерывны на отрезке [a>b], дифференцируемы на интервале 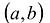и при этом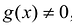, то найдется точка 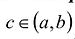для которой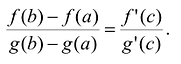

Правила Лопиталя

Пусть f(х) и g(x) - функции, определенные и дифференцируемые в окрестности точки а, где а - конечное число ил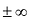и (если 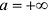, то под окрестностью точки а понимаем какой-нибудь луч 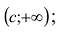если 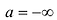, то окрестность - луч (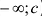)). В самой точке а функции могут быть не определены. Пусть 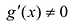при .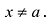

I правило. Если:

1.

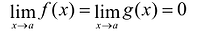
2. Существует конечный или бесконечный предел

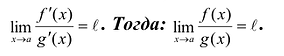
II правило. Если:

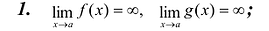
2. Существует конечный или бесконечный предел

Правила Лопиталя позволяют раскрывать неопределенности вида 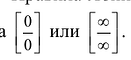Однако, они могут быть использованы и при раскрытии неопределенностей других видов: 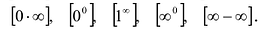Для этого исследуемое выражение

преобразуют так, чтобы получилась неопределенность вида

Примеры:

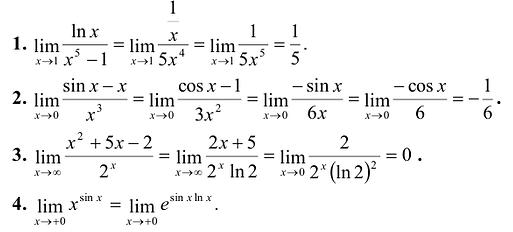
Вычислим: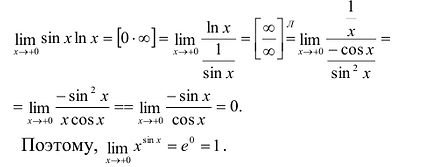

Производные высших порядков

Если функция f(x), определенная в А, имеет производную во всех точках А, то эту производную можно рассматривать как новую функцию g(x) = f'(x), .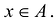

К этой функции применимы все предельные законы, в том числе и дифференцирование.

Если g(x), определенная в А, имеет конечную производную g'(x) в точке 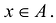, то значение этой производной является второй производной функции f(x).

Аналогично вычисляются производные более высоких порядков.

Дифференциальное исчисление функции одной переменной

К понятию производной приводит экономическая задача о производительности труда.

Пусть функция 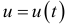выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент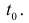

За период времени от 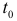до количество продукции изменится от значения  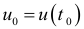до значения 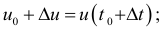тогда средняя производительность труда за этот период времени 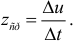Очевидно, что производительность труда в момент 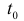можно определить как предельное значение средней производительности за период времени от 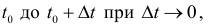т.е.

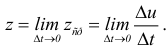
Замечание. Вычислять значение производной и, вообще, дифференцировать функцию можно только на участках её непрерывности. В таком случае говорят о дифференцируемости функции.
 

Определение производной

Допустим, что определена функция у = f(x). Возьмем определенное значение независимой переменной х, значение функции в этой точке у = f(x). При значении аргумента 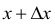получаем  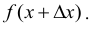Приращению независимой переменной 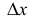соответствует, таким образом, приращение зависимой переменной:

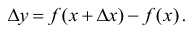
Составим отношение приращения функции к приращению аргумента и найдем предел этого отношения при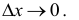

Если этот предел существует, то его называют производной данной функции

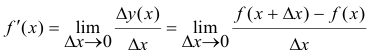
Определение. Производной данной функции 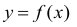по аргументу х
называется предел отношения приращения функции 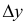к приращению аргумента 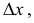когда последнее произвольным образом стремится к нулю.

Операция нахождения производной от функции f(х) называется дифференцированием этой функции.

Наряду с обозначением f'(х) употребляются и другие обозначения,
например

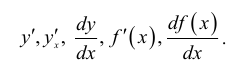
Значение производной при х = а обозначается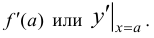

Схема вычисления производной

Производная от данной функции 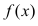может быть найдена по следующей
схеме:

1. Дать аргументу х приращение 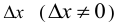и вычислить значение функции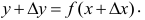
2. Определить приращение функции
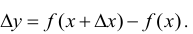
3. Найти отношение 
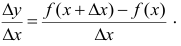
4. Найти предел данного отношения при 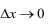(если этот предел существует)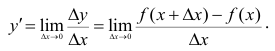

Зависимость между непрерывностью функции и дифференцируемостью

Теорема. Если функция у = f(х) дифференцируема в точке 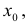то она в этой
точке непрерывна.

Доказательство: по условию функция у = f(x) дифференцируема в точке
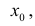т.е. существует конечный предел 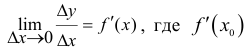- постоянная  величина, не зависящая от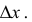

Тогда на основании теоремы о связи бесконечно малых с пределами функций можно записать

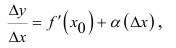
где 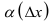- бесконечно малая величина при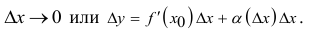
При 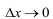на основании свойств бесконечно малых устанавливаем, что 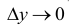и, следовательно, по определению функция 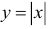в точке 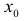является непрерывной.

Обратная теорема, вообще говоря, неверна, т.е. если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Например, функция у = |х| непрерывна в точке х = 0, но она не дифференцируема в этой точке.

Геометрический смысл производной

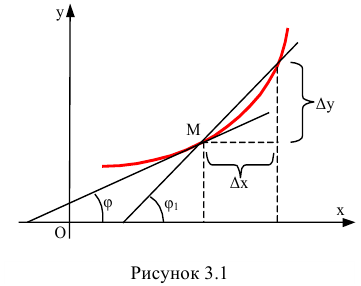
Из рисунка 3.1 видно, что производная 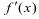от функции 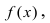вычисленная при заданном значении х, равна тангенсу угла, образованного    положительным направлением оси Ох и касательной, проведенной к графику этой функции в точке с абсциссой х.

С другой стороны, тангенс этого угла не что иное, как угловой коэффициент прямой линии (в данном случае касательной к графику)

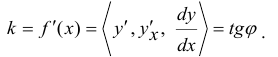
Итак, если функция дифференцируема в данной точке, то геометрический смысл производной следующий: производная есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у = f(х) в точк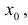е т.е.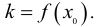 

Вычисленное в какой-либо точке значение производной характеризует скорость функции в этой точке.

Свойства производной

1.    Производная постоянной равна нулю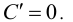

Доказательство.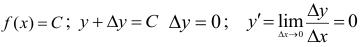

2.    Производная аргумента равна единице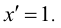 

Доказательство.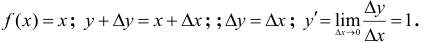

3.    Производная суммы (разности) равна сумме (разности) производных

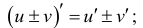
где 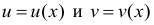- дифференцируемые функции.

4.    Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.

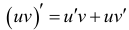
5.    Производная частного двух дифференцируемых функций находится по формуле

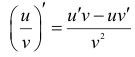 при условии, что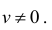 
 

Производная сложной и обратной функции

Пусть переменная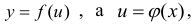 т.е. задана сложная функция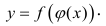 

Теорема. Если 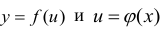- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е.

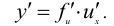
Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е.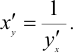
 

Производные основных элементарных функций

1.    Производная от степенной функции 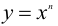при вещественном n равна произведению показателя степени на степенную функцию, у которой показатель на единицу меньше,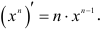

Найдем производную от функции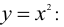

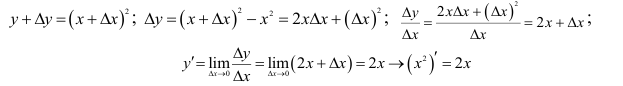
Найдем производную от функции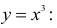

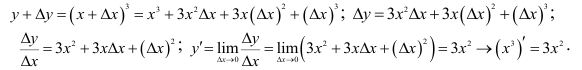
Подобным образом могут быть найдены и прочие производные степенной функции. В итоге получим

2.    Производная показательной функции

а)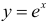

Прологарифмируем обе части по основанию е, получим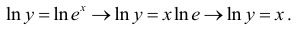

Дифференцируя обе части по переменной и учитывая, что In у - сложная
функция, получим 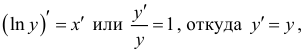т.е.

и

б) 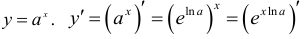 и по правилу дифференцирования сложной функции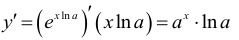 

Итак,

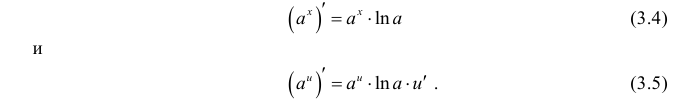
Таблица основных производных

 

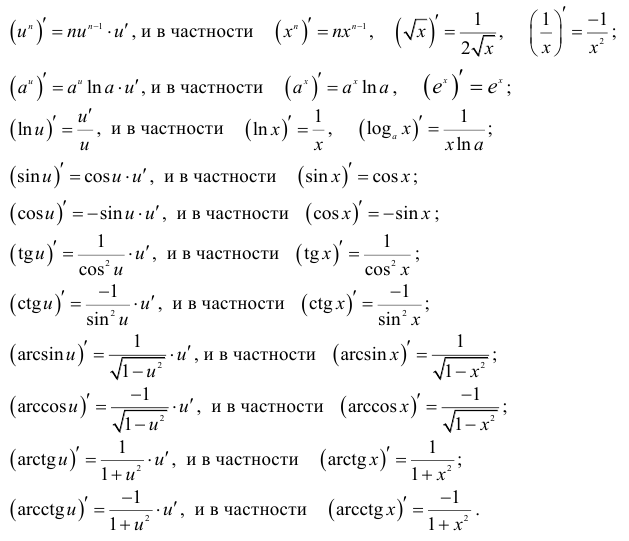
Пример:

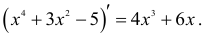
Пример:

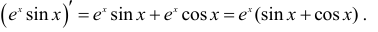
Пример:

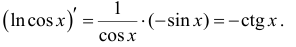
Дифференцирование неявной функции

Пусть значения двух переменных х и у связаны между собой некоторым уравнением, которое символически обозначается так: F(x,y) = 0.

Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способы её задания. Каждая явная функция у= f(x) может быть представлена и как неявная у - f(х) = 0.

Если неявная функция задана уравнением F(x,y) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у. Достаточно продифференцировать это уравнение по х, а полученное уравнение по возможности разрешить относительно производной.

Заметим, что во многих случаях величина производной будет являться функцией не только х, но и у.

Пример:

Функция задана в виде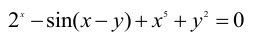

Дифференцируем данную функцию почленно

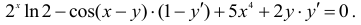
Оставим данное выражение, не разрешая его относительно производной. Кстати, разрешение результатов дифференцирования относительно производной удается далеко не всегда.

Пример:

Функция задана в виде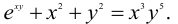

Дифференцируем данную функцию почленно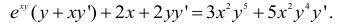

Разрешая полученное выражение относительно производной, получим уеху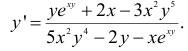
 

Производные высших порядков

Ранее мы находили выражения для производных от различных функций. При этом производные являлись также некоторыми функциями того же аргумента. Следовательно, процесс дифференцирования может быть повторен.

Производные высших порядков являются результатом последовательного дифференцирования функции.

Назовем функцию нулевой производной, а производную данной функции назовем первой производной, производную от первой производной назовем второй производной, и так далее.

N-ой производной назовем производную (если она существует) от (N-1)
производной.

Обозначения

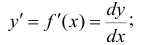
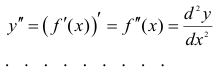(читается так: «дэ два игрек по дэ икс дважды»);
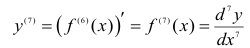(читается так: «дэ семь игрек по дэ икс семь раз»);

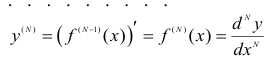(читается так: «дэ эн игрек по дэ икс эн раз»).

Принято при обозначении первых трех производных использовать штрихи, а далее цифры в круглых скобках.

Пример №1

Найти третью производную функции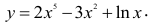

Решение.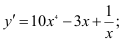 

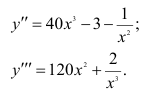
/' = 40л-’-з-Л;

Пример №2

Найти пятую производную функции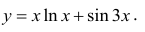

Решение.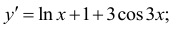 

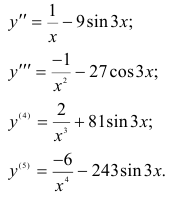
Из задачи о производительности труда следует, что производная объема произведенной продукции по времени 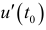есть производительность труда в момент времени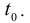

Производная функции в точке

Пусть функция 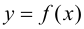определена в некоторой окрестности точки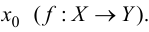

Определение 5.1. Если предел отношения приращения функции 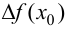к соответствующему приращению аргумента  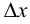при 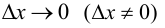существует и конечен, то он называется производной функции 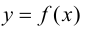в точк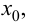е т. е.

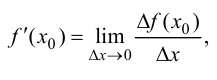
иначе

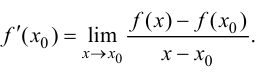
Обозначения: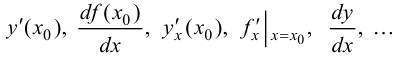

Нахождение производной функции 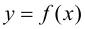называется дифференцированием этой функции.

Геометрический смысл производной функции в точке

Пусть 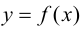- непрерывная функция, определенная в некоторой окрестности точки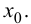

Рассмотрим две точки графика этой функци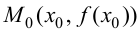и: и 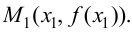Прямая 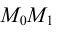- секущая 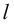(рис. 5.1). Обозначим:

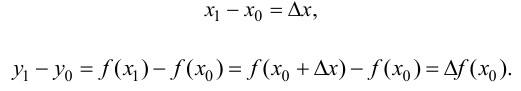
Найдем угловой коэффициент этой прямой. Из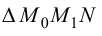
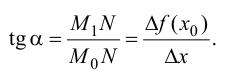  (5.1)
Из (5.1) следует, что 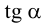зависит только от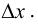

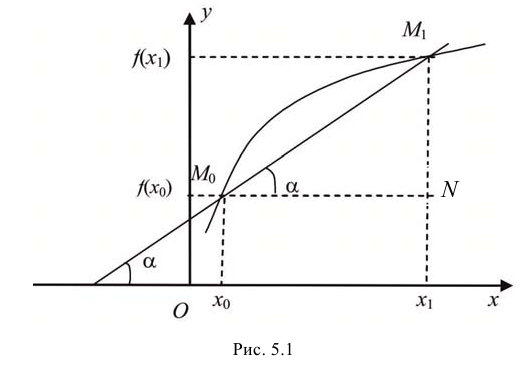
При перемещении точки 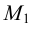к точке 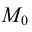по графику непрерывной функции 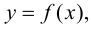секущая 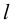будет стремиться к некоторому предельному положению: касательной к графику функции 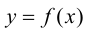в точке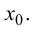

Так как 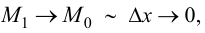то угловой коэффициент касательной, проведенной к графику функции 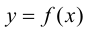в точке 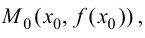можно получить предельным переходом из (5.1):

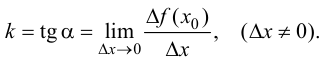
Уравнение касательной, как известно, определяется формулой

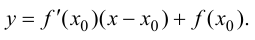
Вывод. Производная функции 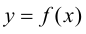в точке  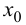равна угловому коэффициенту касательной, проведенной к графику функции в точке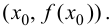 

Физический смысл производной функции

Пусть точка 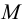 движется прямолинейно и 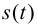- путь, проходимый ею за время  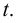Тогда отношение пути 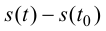ко времени 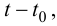есть средняя скорость движения точки за это время

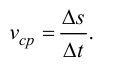(5.2)

Если существует предел (5.2) при 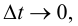то он называется мгновенной скоростью движения точки в момент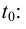

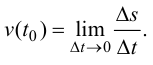
Вывод. Мгновенная скорость есть производная пройденного пути 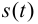 по времени 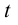в данный момент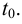

Непрерывность функции, имеющей производную

При определении понятия производной функции 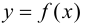в точке 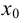предполагалось, что функция определена в точке 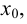а также и в некоторой достаточно малой ее окрестности, и существует

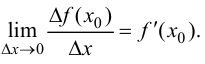
Исследуем вопрос о непрерывности функции 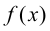в точке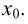

Теорема 5.1. Если функция 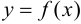определена на множестве  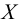и в точке 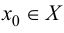имеет конечную производную 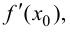то 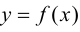непрерывна в точке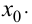 

Доказательство.

По условию

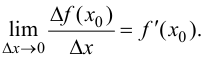
По определению предела имеем

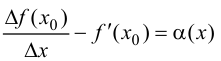
где 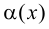- БМФ при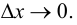

Тогда 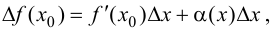откуда видно, что при  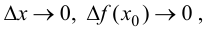т. е. 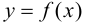непрерывна в точке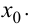 

Замечание 5.1. Обратное утверждение неверно: из непрерывности функции в точке не следует существование производной в этой точке.

Определение 5.2. Односторонними производными функции 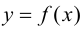 в точке 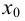называются  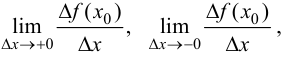если они существуют.

Обозначение: 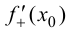 и

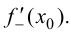
Очевидно, что если в точке 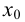существует производная, то существуют и односторонние производные и они равны между собой.

Пример №3

Показать, что функция 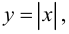непрерывная в точке 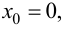не имеет производной в этой точке.

Решение.

Покажем отсутствие производной в точке 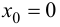для функции  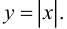Для этого найдем односторонние производные данной функции в точке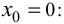

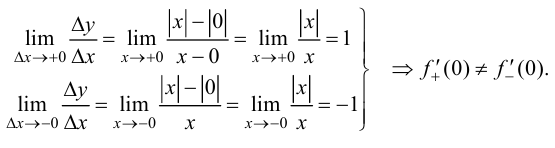
Вывод. Так как односторонние производные функции 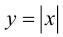в точке 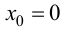существуют, но не равны между собой, то функция не имеет производной в этой точке.

Таблица производных

Постоянная функция:

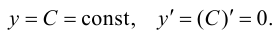
Степенная функция:

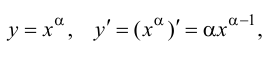
в частности

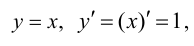
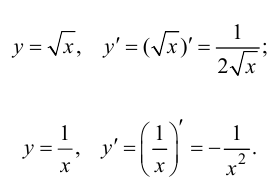
Показательная функция:

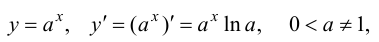
в частности,

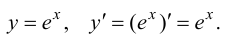
Логарифмическая функция:

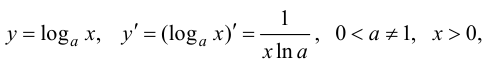
в частности,

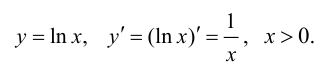
Тригонометрические функции:

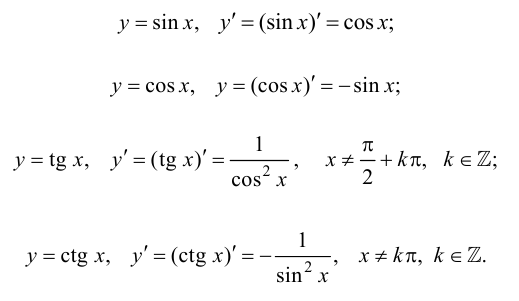
Обратные тригонометрические функции:

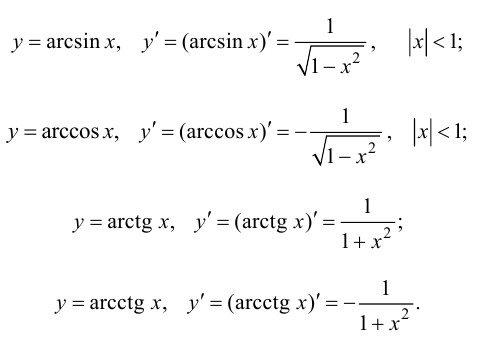
Гиперболические функции:

• -  синус гиперболический
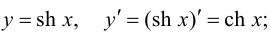
• -  косинус гиперболический
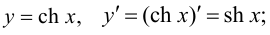
• -  тангенс гиперболический 
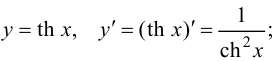
• -  котангенс гиперболический

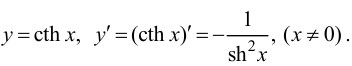
Правила дифференцирования

Функция 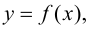имеющая производную в точке  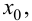называется дифференцируемой в этой точке.

Функция, дифференцируемая во всех точках множества 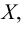 называется дифференцируемой на этом множестве, обозначается

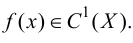
Вычисление производной алгебраической суммы, произведения и частного функций

Теорема 5.2. Если функци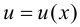и и 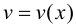дифференцируемы в точке  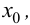то функции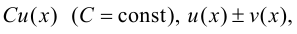
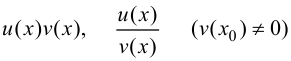
также дифференцируемы в этой причем:
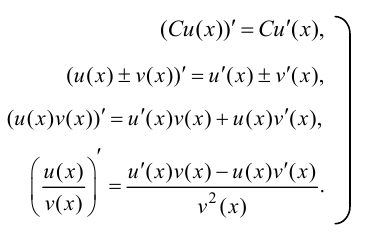      (5.3)
(5.3) - основные формулы дифференцирования.

Доказательство. Докажем первые три формулы.

1. Рассмотрим функцию 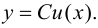Тогда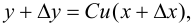

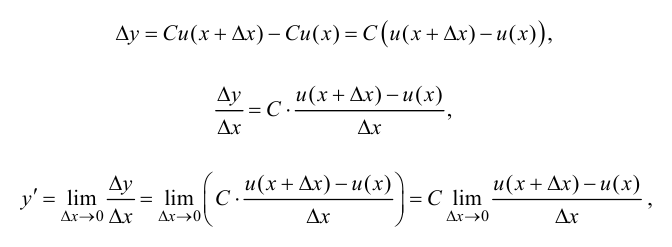
т. е.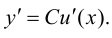 

2. Рассмотрим функцию 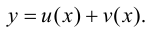Тогда

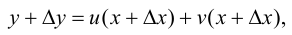
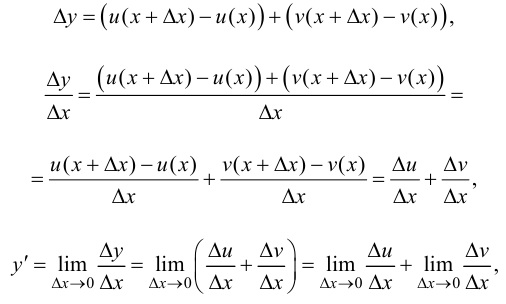
т. е. 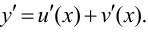 Случай 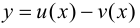доказывается аналогично.

3. Рассмотрим функцию 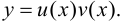 Тогда

Рассмотрим последний член в правой части формулы: 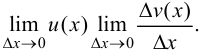 Так как 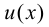- дифференцируемая функция, то она непрерывна. Следовательно,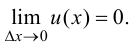  

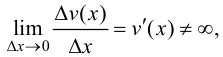 так как 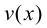- дифференцируемая функция.

Таким образом, рассматриваемый член равен нулю, и окончательно получаем: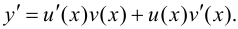 

• Заказать решение задач по высшей математике

Пример №4

Найти производную функции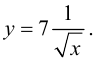

Решение.

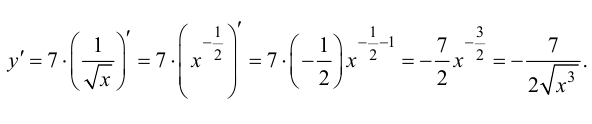
Ответ: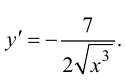 

Пример №5

Найти производную функции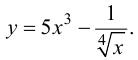

Решение.

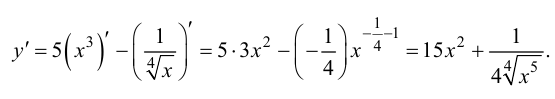
Ответ: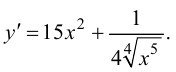

Пример №6

Найти производную функции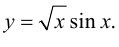

Решение.

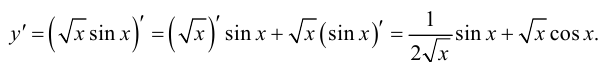
Ответ: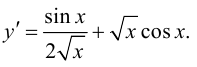 

Пример №7

Найти производную функции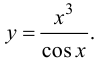

Решение.

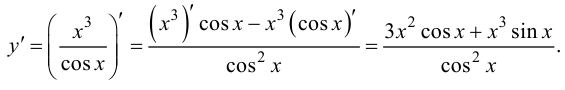
Ответ: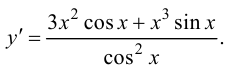

Производная сложной функции

Теорема 5.3. Если функция 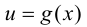дифференцируема в точке  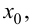а функция 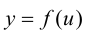дифференцируема в точке 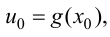то сложная функция 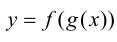дифференцируема в точке 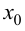и

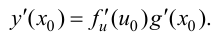    (5.4)

Доказательство.

Так как функция 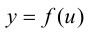 дифференцируема в точке 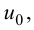то приращение этой функции в точке 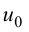может быть записано в виде

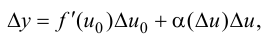    (5.5)

где 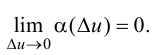Разделим равенство (5.5) на  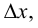получим

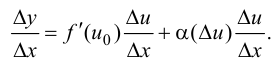    (5.6)

Равенство (5.6) справедливо для любых достаточно малых 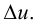 Возьмем 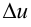равным приращению функции  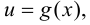соответствующему приращению 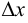аргумента 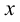в точке  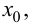и устремим в этом равенстве 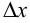к нулю. Так как по условию функция 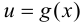имеет в точке  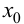производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывност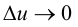и, при 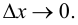Но тогда и 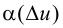также стремится к нулю, т. е. имеем

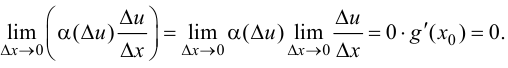   (5.7)

В силу соотношения (5.7) существует предел правой части равенства (5.6) при 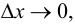равный 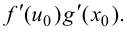Значит, существует предел при  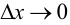и левой части равенства (5.6), который, по определению производной, равен производной сложной функции 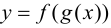в точке  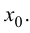Тем самым доказана дифференцируемость сложной функции и установлена формула (5.4). 

Замечание 5.2. Формула (5.4) может быть усложнена. Например, если 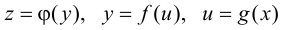и все три функции имеют производные в соответствующих точках, то

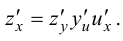    (5-8)

Пример №8

Найти производную функции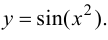

Решение.

Данную функцию можно представить в ви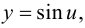де  где 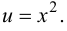 Тогда, по формуле (5.4), получаем

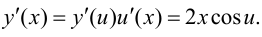
Заменяя на 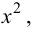 окончательно получим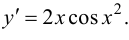

Ответ: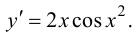

Пример №9

Найти производную функции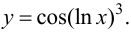 

Решение.

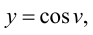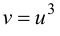Данную функцию можно представить в виде где а 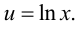Используя формулу (5.8), получаем

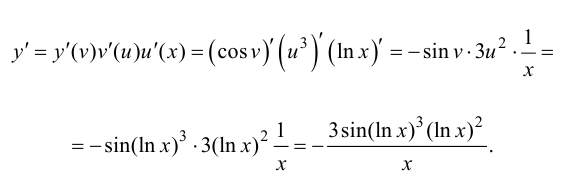
Ответ: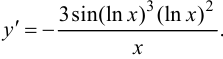

Производная обратной функции

Пусть 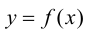и 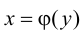- взаимно обратные функции.

Теорема 5.4. Если функция 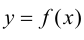строго монотонна на интервале 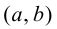и имеет отличную от нуля производную  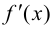в произвольной точке этого интервала, то обратная ей функция 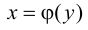также имеет производную 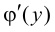в соответствующей точке, определяемую равенством 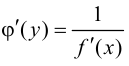или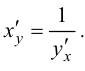

Доказательство.

Рассмотрим обратную функцию 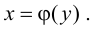Придадим аргументу  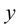приращение 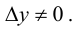Ему соответствует приращение 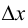обратной функции, причем 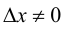в силу строгой монотонности функции  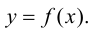Поэтому можно записать

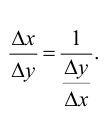     (5.9)

Если 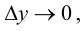то в силу непрерывности обратной функции приращение 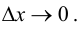Так как 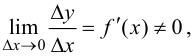то из (5.9) следуют равенства  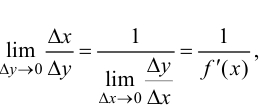т. е.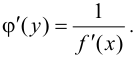 

Правило дифференцирования обратной функции записывают следующим образом:

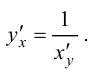
Пример №10

Пользуясь правилом дифференцирования обратной функции, найти производную 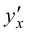для функции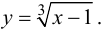

Решение.

Обратная функция 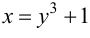 имеет производную  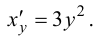Следовательно,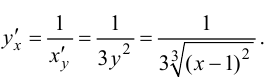

Ответ: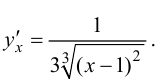

Пример №11

Пользуясь правилом дифференцирования обратной функции, найти производную 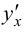 для функции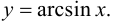

Решение.

Обратная функция 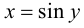имеет производную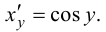

Следовательно,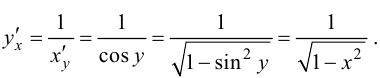

Ответ: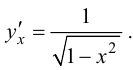

Производная функции, заданной неявно

В ряде задач приходится сталкиваться с ситуацией, когда переменная 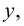 являющаяся по смыслу функцией от  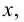задается уравнением  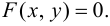В этом случае говорят, что  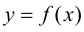как функция аргумента 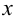задана неявно. Заметим, что не всякую неявно заданную функцию можно представить явно.

Пример №12

Равенство 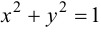определяет две функци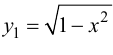и

 и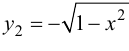

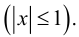
Равенство 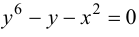нельзя разрешить относительно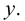 

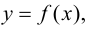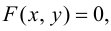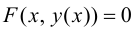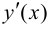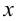Чтобы найти производную функции заданной неявно уравнением нужно продифференцировать тождество как сложную функцию и затем выразить  через  и 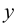из полученного уравнения.

Пример №13

Найти производную функци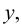и  если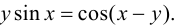 

Решение.

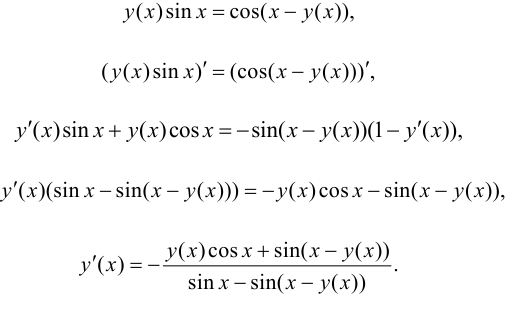
Ответ: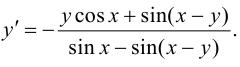

Производная функции, заданной параметрически

Пусть зависимость между аргументом 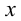и функцией 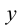задана параметрически в виде двух уравнений

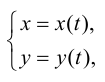   (5.10)

где 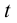 - параметр.

Найдем производную 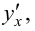считая, что функции (5.10) имеют производные и что функция 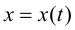имеет обратную  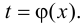По правилу дифференцирования обратной функции

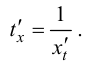    (5.11)

Функцию 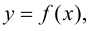определяемую параметрическими уравнениями (5.10), можно рассматривать как сложную функцию 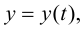где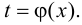

По правилу дифференцирования сложной функции имеем

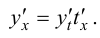
С учетом равенства (5.11) получаем 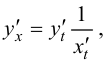 т. е.

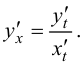    (5-12)

Формула (5.12) позволяет находить производную 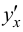 от функции заданной параметрически, не находя зависимость  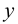от 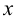в явном виде.

Пример №14

Пусть 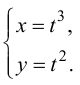 Найти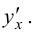  

Решение.

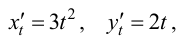
поэтому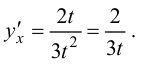 

Если непосредственно найти зависимость 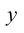 от 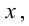 то получим

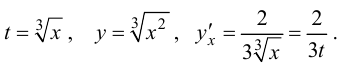
Ответ: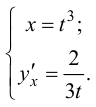

Логарифмическая производная

Пусть необходимо найти производную функции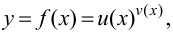  

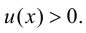
Прологарифмируем обе части равенства 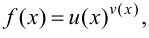 получим 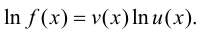Продифференцируем

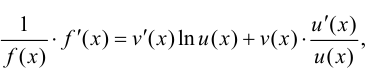
и преобразуем

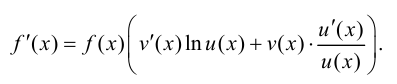
Таким образом,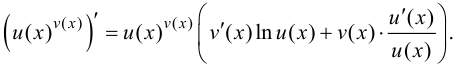 

Пример №15

Найти производную функции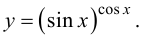 

Решение.

Логарифмируем исходную функцию

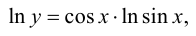
дифференцируем полученное равенство:

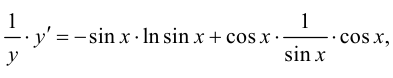
откуда выражаем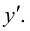

Ответ: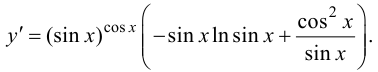

Производные высших порядков

Пусть функция 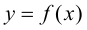определена на множестве  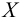и имеет производную в точке 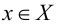и некоторой ее окрестности. Тогда производная функции 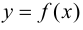в точке 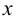есть функция 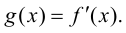Если функция 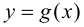имеет производную 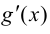в точке 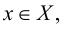то функцию 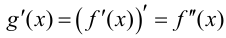называют производной второго порядка функции  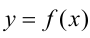и обозначают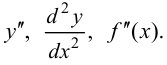 

Вторая производная функции 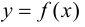может существовать в точке 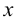и некоторой ее окрестности. Тогда, если существует производная второй производной, то ее называют производной третьего порядка и обозначают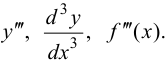

Продолжив аналогичные рассуждения, получим, что если функция 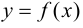имеет в точке 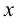и некоторой ее окрестности все производные до 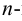го порядка включительно, то производная от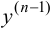

будет представлять собой производную 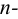го порядка. Если при этом 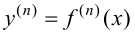- непрерывная функция на множестве 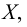то функция 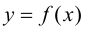называется  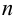раз непрерывно дифференцируемой функцией или функцией класса  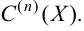Функция, имеющая производную любого порядка, называется бесконечно дифференцируемой.

Пример №16

Функция 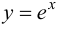- бесконечно дифференцируемая функция на множестве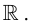

Если 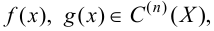то

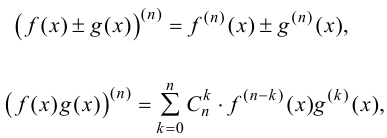    (5.13)

где 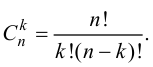 Формула (5.13) называется формулой Лейбница.