
Дифференциальное исчисление - определение и вычисление с примерами решения
Содержание:
Дифференциальное исчисление
Понятие производной
Приращение аргумента и функции
Пусть дан график непрерывной функции.
Определение: Разность между конечным и начальным значениями аргумента называется его приращением, т.е. 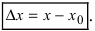
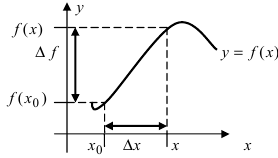
Рис. 69. Приращения аргумента и функции
Теорема: Если 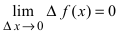 , то функция
, то функция  непрерывна в точке
непрерывна в точке 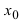 .
.
Доказательство: Приращение функции 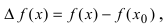 следовательно, функция
следовательно, функция 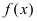 определена как в самой точке
определена как в самой точке 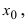 так и в ее
так и в ее 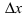 -окрестности. При
-окрестности. При 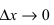 аргумент
аргумент 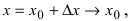 поэтому
поэтому
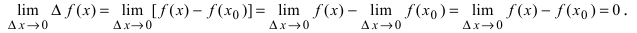
Отсюда следует, что 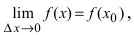 следовательно, функция
следовательно, функция 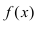 непрерывна в точке
непрерывна в точке 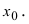
Задачи, приводящие к понятию производной
1. Физика. Пусть материальная точка движется прямолинейно согласно закону 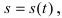 где s - путь, который проходит точка за время t. Требуется определить скорость движения точки в момент времени
где s - путь, который проходит точка за время t. Требуется определить скорость движения точки в момент времени 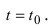 Обозначим через
Обозначим через 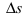 путь, пройденный за время
путь, пройденный за время 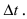 Очевидно, что
Очевидно, что 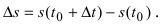 Средняя скорость, с которой движется точка определяется как
Средняя скорость, с которой движется точка определяется как 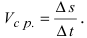 Для того чтобы определить скорость в момент времени
Для того чтобы определить скорость в момент времени 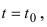 вычислим предел
вычислим предел 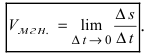
2. Геометрия. Пусть дан график функции 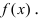 Требуется найти такую прямую линию, которая касается графика функции
Требуется найти такую прямую линию, которая касается графика функции 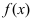 только в одной точке
только в одной точке 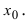
Определение: Касательной называется предельное положение секущей прямой 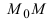 при стремлении
при стремлении 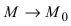 произвольным образом (Рис. 70).
произвольным образом (Рис. 70). 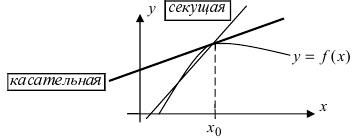
Рис. 70. Касательная к графику функции 
Вычислим тангенс угла наклона секущей 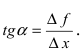 Следовательно, тангенс А х угла касательной к положительному направлению оси абсцисс будет равен предельному значению приведенной выше величины
Следовательно, тангенс А х угла касательной к положительному направлению оси абсцисс будет равен предельному значению приведенной выше величины 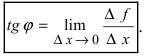
Производная функции. Ее механический и геометрический смысл
Определение: Производной функции 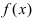 в точке
в точке 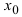 называется предел отношения приращения функции
называется предел отношения приращения функции 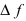 к приращению аргумента
к приращению аргумента 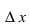 при стремлении по- средней величины к нулю произвольным образом, т.е.
при стремлении по- средней величины к нулю произвольным образом, т.е. 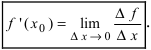
Из рассмотренных выше задач следует, что с точки зрения механики производная определяет мгновенную скорость движения, а с геометрической точки зрения производная функции равна тангенсу угла наклона касательной к положительному направлению оси абсцисс в заданной точке, в которой вычисляется значение производной.
Уравнение касательной и нормали в заданной точке графика функции f(x)
Пусть дан график функции  (Рис. 71):
(Рис. 71):
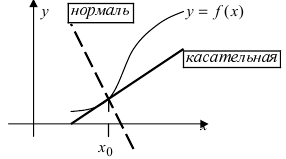
Рис. 71. Касательная и нормаль.
Требуется составить уравнения касательной и нормали в точке  Для составления уравнения касательной воспользуемся уравнением прямой с угловым коэффициентом:
Для составления уравнения касательной воспользуемся уравнением прямой с угловым коэффициентом: 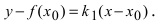 В силу того, что
В силу того, что 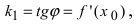 уравнение касательной имеет вид:
уравнение касательной имеет вид:
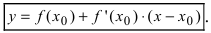
Так как нормаль перпендикулярна к касательной, то ее угловой коэффициент 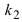 связан с угловым коэффициентом касательной соотношением:
связан с угловым коэффициентом касательной соотношением: 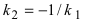 .
.
Следовательно, уравнение нормали имеет следующий вид:
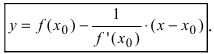
Пример:
Найти угловой коэффициент касательной в точке 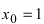 к графику функции
к графику функции 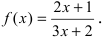
Решение:
Так как 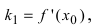 то вычислим производную функции, используя определение производной:
то вычислим производную функции, используя определение производной: 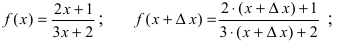
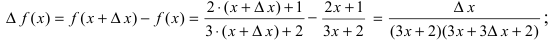
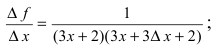 следовательно,
следовательно, 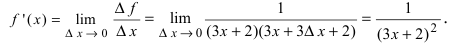
Вычислим значение производной в точке 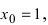 а тем самым и угловой коэффициент касательной в заданной точке
а тем самым и угловой коэффициент касательной в заданной точке 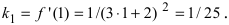
Дифференцируемость непрерывных функций
Определение: Нахождение конечной производной от непрерывной функции называется дифференцированием.
Теорема: Если функция 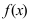 дифференцируема в точке
дифференцируема в точке 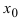 , то в этой точке функция
, то в этой точке функция 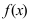 непрерывна.
непрерывна.
Доказательство: Если функция 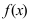 дифференцируема в точке
дифференцируема в точке 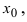 то в этой точке существует конечный предел
то в этой точке существует конечный предел 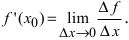 . Используя свойство 4 для бесконечно малых функций (см. Лекцию № 12), можно записать, что
. Используя свойство 4 для бесконечно малых функций (см. Лекцию № 12), можно записать, что 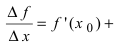
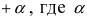 - бесконечно малая функция в
- бесконечно малая функция в 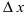 -окрестности точки
-окрестности точки 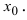 Отсюда следует, что
Отсюда следует, что 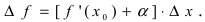 Вычислим предел этого выражения при
Вычислим предел этого выражения при 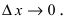 Так как при
Так как при 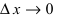 функция
функция 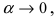 как бесконечно малая функция, а производная остается неизменной, то
как бесконечно малая функция, а производная остается неизменной, то 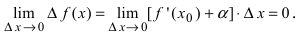
По теореме получаем, что функция 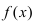 непрерывна в точке
непрерывна в точке 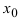 . В силу произвольности точки
. В силу произвольности точки 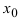 функция
функция 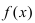 будет непрерывна в любой точке своей области определения.
будет непрерывна в любой точке своей области определения.
Замечание: Утверждение, обратное к рассмотренному в теореме что всякая непрерывная в точке 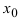 функция будет в этой точке дифференцируема, будет верным не во всех случаях, т.е. не всякая непрерывная функция является дифференцируемой.
функция будет в этой точке дифференцируема, будет верным не во всех случаях, т.е. не всякая непрерывная функция является дифференцируемой.
Пример:
Дифференцируема ли функция 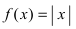 в точке
в точке 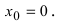 Изобразим график данной функции (Рис. 72):
Изобразим график данной функции (Рис. 72): 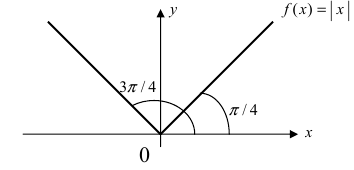
Рис. 72. График функции 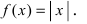
Решение:
В точке 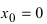 данная функция
данная функция 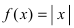 определена, имеет равные леао- и правосторонние пределы (пределы равны нулю), которые равны значению функции в этой точке, следовательно, функция
определена, имеет равные леао- и правосторонние пределы (пределы равны нулю), которые равны значению функции в этой точке, следовательно, функция 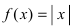 непрерывна в точке
непрерывна в точке 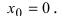 Однако в этой точке производная не существует, так как слева
Однако в этой точке производная не существует, так как слева 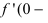 ,
, 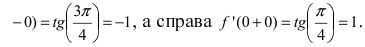 Отсюда следует, что в точке
Отсюда следует, что в точке 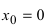 производной нет.
производной нет.
Пример:
Дифференцируема ли функция 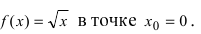
Решение:
В точке 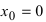 данная функция
данная функция 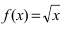 непрерывна (доказать самостотельно). Производная функции равна
непрерывна (доказать самостотельно). Производная функции равна
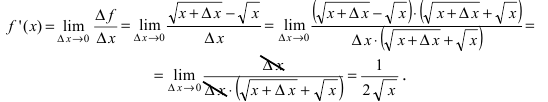
Следовательно, в точке 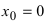 производная
производная 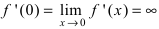 бесконечна, и функция не дифференцируема.
бесконечна, и функция не дифференцируема.
Правила дифференцирования
Вычисление производной согласно определению является трудоемкой задачей. В связи с этим были получены следующие правила дифференцирования:
1. Производная от суммы (разности) двух функций равна сумме (разности) производных от этих функций, т.е. 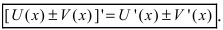
Доказательство: Пусть 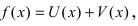 тогда в приращенной точке функция равна
тогда в приращенной точке функция равна 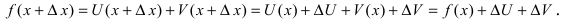
Приращение функции будет равно: 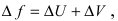 а значит производная от приведенной функции
а значит производная от приведенной функции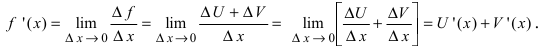
Замечание: Производная от суммы (разности) любого числа функций равна сумме (разности) производных от этих функций.
2. Производная от произведения двух функций вычисляется по формуле: 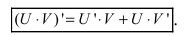
Доказательство: Пусть 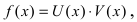 тогда в приращенной точке функция равна
тогда в приращенной точке функция равна 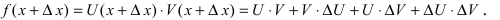
Приращение функции будет равно: 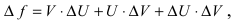 а значит производная от приведенной функции
а значит производная от приведенной функции
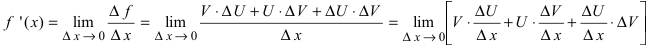 (так функции непрерывны, то при
(так функции непрерывны, то при 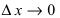 и приращение
и приращение 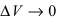 )
)
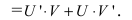
3. Производная от частного двух функций вычисляется согласно формуле:
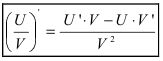 (доказать самостоятельно).
(доказать самостоятельно).
4. Производная от обратной функции вычисляется по формуле: 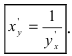
Доказательство: Так как 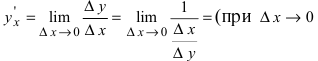 и приращение
и приращение 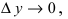 следовательно,)
следовательно,) 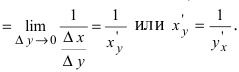
5. Производная от сложной функции 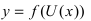 вычисляется по формуле:
вычисляется по формуле: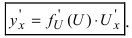
Доказательство: Так как 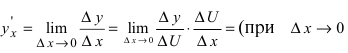 и приращение
и приращение 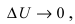 следовательно,) =
следовательно,) = 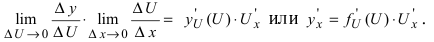 Лекция № 17 “Производная от элементарных, параметрически и неявно заданных функций”
Лекция № 17 “Производная от элементарных, параметрически и неявно заданных функций”
Производная от основных элементарных функций
1. Постоянная функция 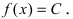 Вычислим приращение постоянной функции
Вычислим приращение постоянной функции 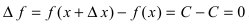 . Отношение приращения функции к приращению аргумента
. Отношение приращения функции к приращению аргумента 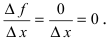 Следовательно,
Следовательно, 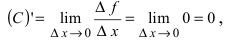 т.е. производная от постоянной величины равна нулю:
т.е. производная от постоянной величины равна нулю: 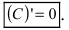
Следствие: При вычислении производной от произведения константы С на функцию 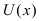 получаем
получаем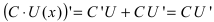 т.е. постоянный множитель можно выносить за знак производной
т.е. постоянный множитель можно выносить за знак производной 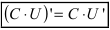 .
.
Следствие: Аналогично поступают при вычислении производной от частного 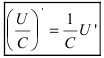 или
или 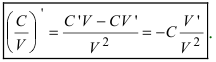
2. Логарифмическая функция 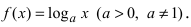 Используя определение производной, находим
Используя определение производной, находим 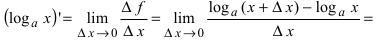
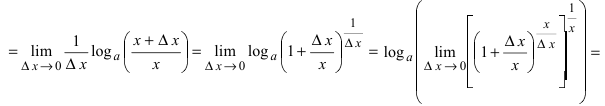 (выражение в квадратных скобках стремится к числу е по второму замеча-1 тельному пределу) =
(выражение в квадратных скобках стремится к числу е по второму замеча-1 тельному пределу) = 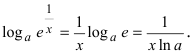
Следствие: Производная от сложной логарифмической функции равна 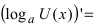
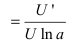 .
.
Следствие: Если основание логарифма 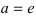 , то
, то 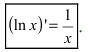
3. Степенная функция 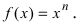 Для нахождения производной от этой функции воспользуемся методом логарифмического дифференцирования, то есть
Для нахождения производной от этой функции воспользуемся методом логарифмического дифференцирования, то есть
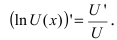 Возьмем натуральный логарифм от степенной функции
Возьмем натуральный логарифм от степенной функции
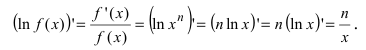
Отсюда находим 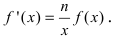 Таким образом,
Таким образом, 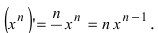 Для сложной функции эта формула имеет следующий вид
Для сложной функции эта формула имеет следующий вид 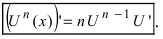
Следствие: Наиболее распространенными являются случаи:
- а)
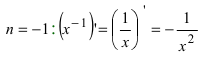
- б)
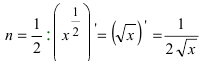 ;
; - в)
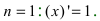
4. Показательная функция 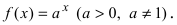 Воспользуемся логарифмическим дифференцированием
Воспользуемся логарифмическим дифференцированием 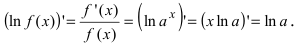 Отсюда находим
Отсюда находим 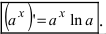 Для сложной функции эта формула имеет следующий вид
Для сложной функции эта формула имеет следующий вид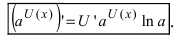
Следствие: Если основание показательной функции а=е, то 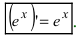 В случае сложной функции производная равна
В случае сложной функции производная равна 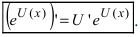
5. Тригонометрические функции: a) 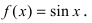 Вычислим производную от синуса
Вычислим производную от синуса 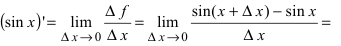
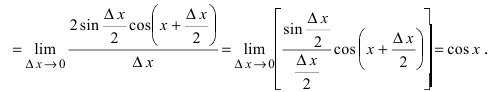
Следовательно, 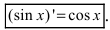 При выводе формулы был использован первый замечательный предел (см. Лекцию № 14). Для сложной функции производная равна
При выводе формулы был использован первый замечательный предел (см. Лекцию № 14). Для сложной функции производная равна 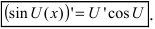 Самостоятельно получить формулы для других тригонометрических функций:
Самостоятельно получить формулы для других тригонометрических функций: 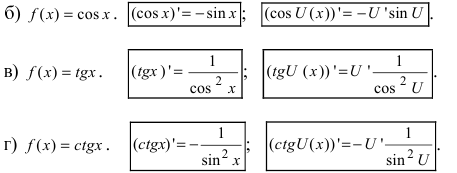
6. Обратные тригонометрические функции:
a) 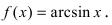 Вычислим производную от арксинуса, для чего от обеих частей равенства возьмем функцию синус, то есть найдем обратную функцию
Вычислим производную от арксинуса, для чего от обеих частей равенства возьмем функцию синус, то есть найдем обратную функцию 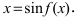 Беря производную от обеих частей равенства с учетом того факта, что функция, стоящая справа, является сложной, получим
Беря производную от обеих частей равенства с учетом того факта, что функция, стоящая справа, является сложной, получим 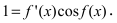 Отсюда находим, что
Отсюда находим, что 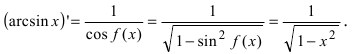 Таким образом,
Таким образом, 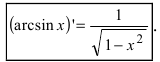 Для сложной функции
Для сложной функции 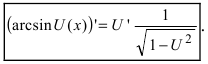 Самостоятельно получить формулы для других обратных тригонометрических функций:
Самостоятельно получить формулы для других обратных тригонометрических функций: 
Пример:
Найти производную функции 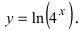
Решение:
По правилу дифференцирования сложной функции и с учетом выражения для логарифмической и показательной функций имеем 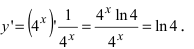
Пример:
Найти производную функции 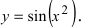
Решение:
В данном случае производная 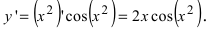
Полученные производные от элементарных функций сведем в таблицу: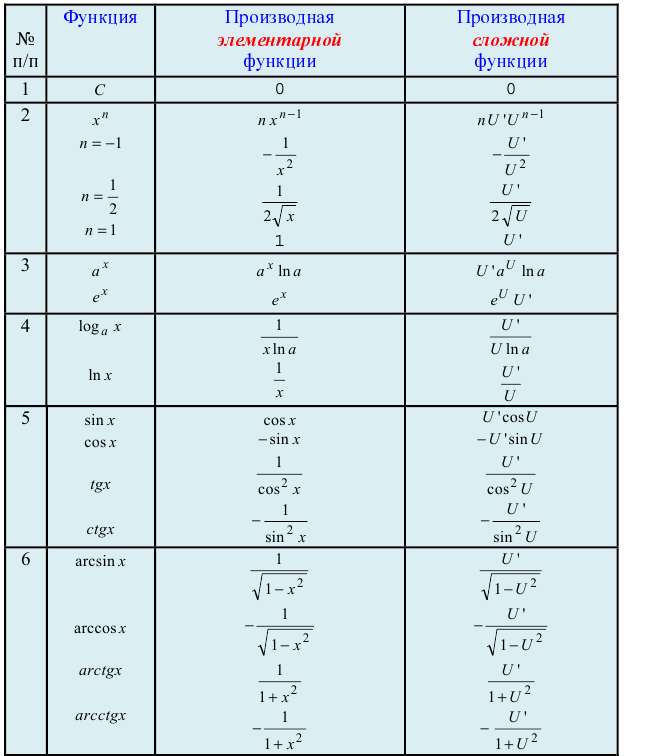
Пример:
Найти производную функции 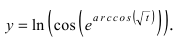
Решение:
По правилу дифференцирования сложной функции 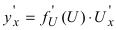 и с учетом выражения для логарифмической
и с учетом выражения для логарифмической 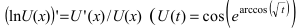 - в данном примере аргументом является переменная t) имеем
- в данном примере аргументом является переменная t) имеем
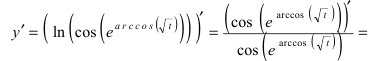 (воспользуемся формулой для ко- синуса
(воспользуемся формулой для ко- синуса 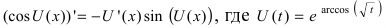
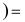
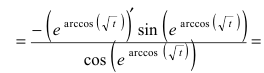 (производная от
(производная от 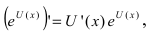 где внутренняя функция
где внутренняя функция 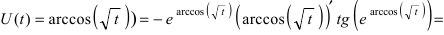 (вычислим производную от сложной функции
(вычислим производную от сложной функции 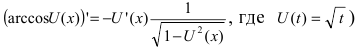
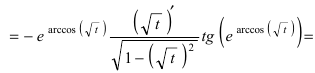 (последняя производная берётся от элементарной функции
(последняя производная берётся от элементарной функции 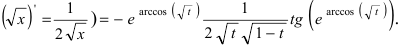
Пример:
Найти производную функции 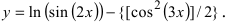
Решение:
По правилу дифференцирования разности функций 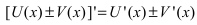 и правила взятия производной от произведения константы С на функцию
и правила взятия производной от произведения константы С на функцию 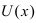
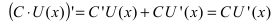 получаем:
получаем: 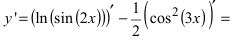 :
:
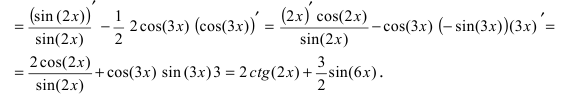
Пример:
Найти производную функции 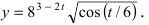
Решение:
По правилу дифференцирования произведения функций 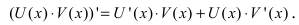
В результате действий, получаем:
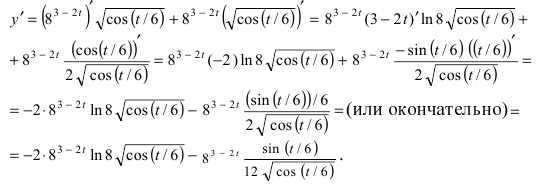
Пример:
Найти производную функции 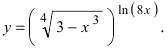
Решение:
По условию задачи дана показательно-степенная функция 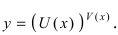 Для отыскания производной от такой функции воспользуемся логарифмическим дифференцированием с применением формулы:
Для отыскания производной от такой функции воспользуемся логарифмическим дифференцированием с применением формулы: 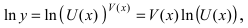
и правила дифференцирования произведения функций
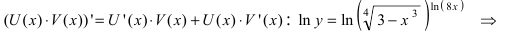
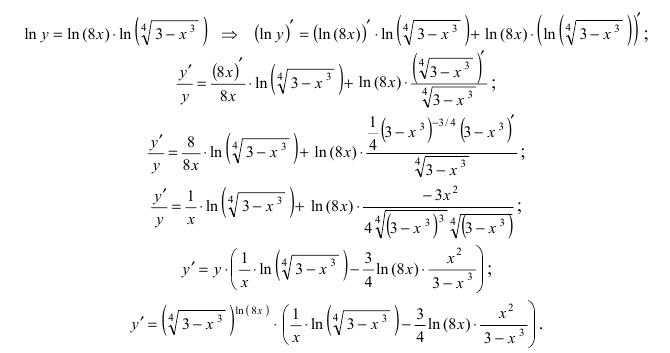
Производная от параметрически и неявно заданных функций
Определение: Если функция 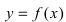 задается в виде системы уравнений
задается в виде системы уравнений 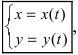 то говорят, что функция задана в параметрическом виде.
то говорят, что функция задана в параметрическом виде.
Чтобы продифференцировать параметрически заданную функцию, надо из первого уравнения системы найти обратную функцию t(x) и подставить ее во второе уравнение системы. В результаты этих действий получается сложная функция, производная от которой равна 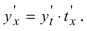 Так как производная от обратной функции связана с производной исходной функции равенством
Так как производная от обратной функции связана с производной исходной функции равенством 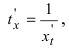 то формула для производной от параметрически заданной функции принимает вид:
то формула для производной от параметрически заданной функции принимает вид: 
Пример:
Найти производную функции 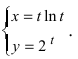
Решение:
Вычислим производные от заданных функций по параметру t:
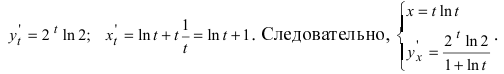
Определение: Если функция y = f(x) задается в виде соотношения F(x, у) = 0, из которого нельзя явно выразить переменную у через х или наоборот, то говорят, что функция задана в неявном виде.
Дифференцирование таких функций осуществляется с учетом того, что переменная у является сложной функцией, т.е. зависит от переменной х.
Пример:
Найти производную функции 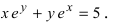
Решение:
Продифференцируем данное соотношение с учетом вышеизложенного материала получим 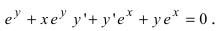 Отсюда находим,
Отсюда находим, 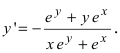 С учетом исходного равенства полученное выражение определяет производную от неявно заданной функции:
С учетом исходного равенства полученное выражение определяет производную от неявно заданной функции: 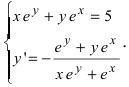
-----вышмат
Дифференциальное исчисление
Производная функции, ее геометрический и физический смыслы
При изучении различных экономических процессов, описываемых функциями, существенную роль играют скорость роста процесса, ускорение роста, оптимальный режим и другие характеристики, которые исследуются с помощью производной.
Рассмотрим геометрическую задачу о проведении касательной к плоской кривой Пусть на плоскости Оху дана непрерывная кривая y=f(x). Необходимо найти уравнение касательной к этой кривой в точке 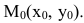 Уравнение прямой, проходящей через точку
Уравнение прямой, проходящей через точку 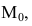 имеет вид:
имеет вид:
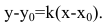
Касательной называется прямая, к которой стремится секущая при стремлении второй точки секущей к первой. Дадим аргументу 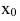 приращение
приращение 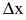 и перейдем на кривой y=f(x) от точки
и перейдем на кривой y=f(x) от точки 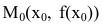 к точке
к точке 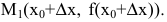 Угловой коэффициент (или тангенс угла наклона) секущей
Угловой коэффициент (или тангенс угла наклона) секущей 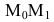 может быть найден по формуле:
может быть найден по формуле: 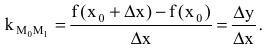 Тогда угловой коэффициент касательной
Тогда угловой коэффициент касательной
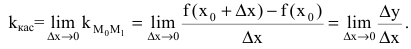
Это и есть производная функции y=f(x) в точке 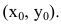 Таким образом, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания (геометрический смысл производной).
Таким образом, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания (геометрический смысл производной).
Производная функции имеет несколько обозначений:
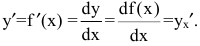
Следовательно, уравнение касательной к кривой y=f(x) в точке 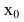 можно записать в виде:
можно записать в виде:
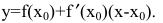
Нахождение мгновенной скорости прямолинейно движущейся точки
Пусть точка М движется прямолинейно и s=f(t) - путь, проходимый ею за время t. Средней скоростью прямолинейного движения за время 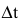 называется отношение пройденного пути к затраченному времени:
называется отношение пройденного пути к затраченному времени: 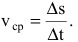 Если существует предел
Если существует предел 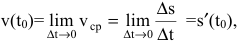 то он называется (мгновенной) скоростью в некоторый момент времени
то он называется (мгновенной) скоростью в некоторый момент времени 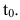 В этом состоит физический смысл производной.
В этом состоит физический смысл производной.
Если v=f(t) - функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени t, то (мгновенное) ускорение материальной точки в фиксированный момент времени 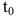 есть производная от скорости по времени:
есть производная от скорости по времени: 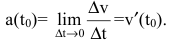
Вывод. Производная есть предел отношения приращения функции к бес- конечно малому приращению аргумента.
Важно отметить, что запись 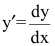 имеет не только символическое значение как способ написания производной, но и смысловое: производная функции есть отношение ее дифференциала dy к дифференциалу аргумента dx.
имеет не только символическое значение как способ написания производной, но и смысловое: производная функции есть отношение ее дифференциала dy к дифференциалу аргумента dx.
Дифференциалом функции одной переменной называется произведение ее производной на приращение аргумента: 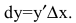 Для функции у=х получаем
Для функции у=х получаем 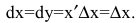 Следовательно, дифференциал независимой переменной равен приращению этой переменной. Отсюда dy=y'dx (подробнее см. литературу).
Следовательно, дифференциал независимой переменной равен приращению этой переменной. Отсюда dy=y'dx (подробнее см. литературу).
Нахождение для заданной функции ее производной называется дифференцированием данной функции. А учение о производной и ее приложениях является предметом дифференциального исчисления. Фундамент дифференциального исчисления составляют основные правила и формулы дифференцирования функций. Используя их, можно найти производную и дифференциал любой элементарной функции.
Основные правила дифференцирования
Внимание! Для существования производной в некоторой точке необходимо, чтобы функция была непрерывна в этой точке. Однако не всякая непрерывная в точке функция имеет в ней производную.
Теорема 1. Производная постоянной равна нулю: с'=0.
Теорема 2. Пусть u=u(x), v=v(x) - дифференцируемые функции. Тогда:
- производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций: (u+v)'=u'+v';
- производная произведения конечного числа дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные: (uv)'=u'v+v'u; в частности, постоянный множитель можно выносить за знак производной: (cu)'=cu';
- производная частного двух дифференцируемых функций может быть найдена по формуле:
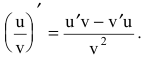
Теорема 3. Производная сложной функции равна ее производной по промежуточному аргументу, умноженной на производную промежуточного аргумента.
Действительно, пусть задана сложная функция y=f[u(x)]. Тогда 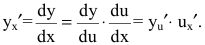
Теорема 4. Производная обратной функции есть величина, обратная производной прямой функции.
Так, если  - взаимно обратные функции и
- взаимно обратные функции и  то
то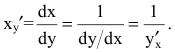
Таблица производных
Приведем основные формулы дифференцирования функций. Пусть u=u(x) - дифференцируемая функция.
Тогда
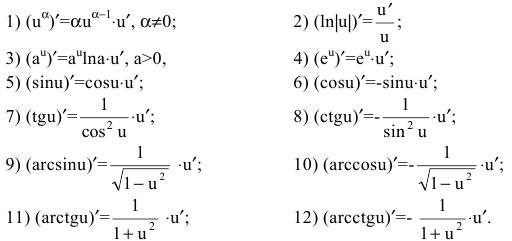
Выведем производные некоторых функций.
1. Если y=sinx, то
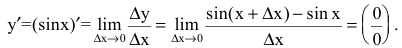
Используя формулу разности синусов
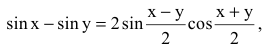 получим
получим 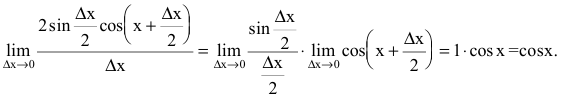
Так как любую тригонометрическую функцию можно вывести через синус, то нетрудно найти производные остальных тригонометрических функций.
2. Пусть y=cosx. Тогда по теореме о производной сложной функции
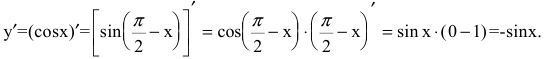
3. Для функции y=tgx воспользуемся правилом дифференцирования частного: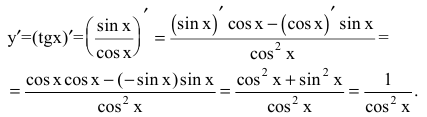
4. Представим y=ctgx как степенную функцию от тангенса. Тогда
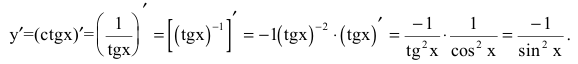 5. Вычислим производную y=arcsinx, где
5. Вычислим производную y=arcsinx, где 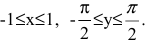 Обратная функция имеет вид x=siny. Причем
Обратная функция имеет вид x=siny. Причем 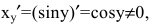 если
если 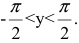 По теореме дифференцирования обратной функции
По теореме дифференцирования обратной функции
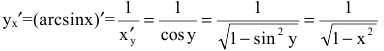
и при х=±1 производная не существует.
6. Производную y=arccosx получим из соотношения 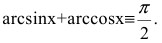 Следовательно,
Следовательно, 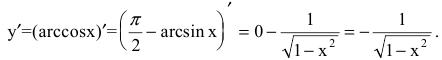
Предельный анализ в экономике
Задача о производительности труда
Пусть функция y=f(t) выражает количество произведенной продукции у за время t и необходимо найти производительность труда в момент времени 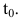 . Очевидно, за период времени от
. Очевидно, за период времени от 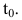 до
до 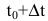 количество произведенной продукции изменится от
количество произведенной продукции изменится от 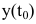 до
до 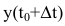 и составит
и составит 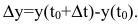
Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е.
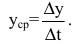
Производительность труда в момент времени 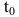 можно определить как предельное значение средней производительности за период времени от
можно определить как предельное значение средней производительности за период времени от 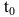 до
до 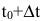 при
при 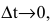 т.е.
т.е.
Пример №34
Объем продукции хлебобулочных изделий, произведенных бригадой пекарей в течение смены, может быть описан функцией
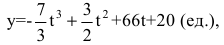
где t - время в часах. Вычислить производительность труда через час после начала работы.
Решение:
Производительность труда выражается производной
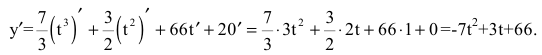
В заданный момент времени соответственно имеем: 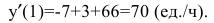
Задача о предельных издержках производства
Издержки производства у будем рассматривать как функцию количества выпускаемой продукции х. Тогда 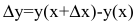 - приращение издержек производства с увеличением объема произведенной продукции на
- приращение издержек производства с увеличением объема произведенной продукции на 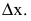 . Среднее приращение издержек производства на единицу продукции есть
. Среднее приращение издержек производства на единицу продукции есть 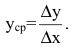 Производная
Производная 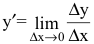 выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельная полезность и другие предельные величины. Таким образом, производная выступает как скорость изменения некоторого экономического процесса во времени или относительно исследуемого фактора.
Для исследования экономических процессов часто используется понятие эластичности функции. Эластичностью функции 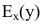 называется предел отношения относительного приращения функции к относительному приращению переменной, если приращение переменной стремится к нулю:
называется предел отношения относительного приращения функции к относительному приращению переменной, если приращение переменной стремится к нулю: 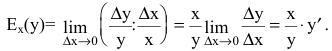 Эластичность дает приближенный процентный прирост функции при изменении независимой переменой на 1%. Например, эластичность спроса у относительно цены х показывает приближенно, на сколько процентов изменится спрос при изменении цены на 1%. Если эластичность спроса по абсолютной величине больше единицы |Ех(у)|>1, то спрос считают эластичным, если |Ех(у)|= 1 - нейтральным, если |Ех(у)|<1 - неэластичным относительно цены.
Эластичность дает приближенный процентный прирост функции при изменении независимой переменой на 1%. Например, эластичность спроса у относительно цены х показывает приближенно, на сколько процентов изменится спрос при изменении цены на 1%. Если эластичность спроса по абсолютной величине больше единицы |Ех(у)|>1, то спрос считают эластичным, если |Ех(у)|= 1 - нейтральным, если |Ех(у)|<1 - неэластичным относительно цены.
Пример №35
Опытным путем установлены функции спроса 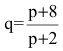 и предложения s=p+0.5, где q и s - количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, р - цена товара. Найти:
и предложения s=p+0.5, где q и s - количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, р - цена товара. Найти:
- 1) равновесную цену, при которой спрос и предложение совпадают;
- 2) эластичность спроса и предложения для этой цены;
- 3) изменение дохода при увеличении цены на 5% от равновесной.
Решение:
1) равновесная цена определяется из условия q=s: 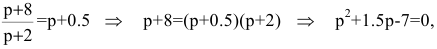 откуда р=2 ден. ед.
откуда р=2 ден. ед.
2) найдем эластичности спроса и предложения:
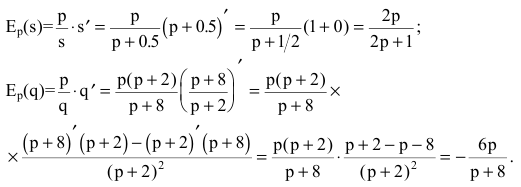
Для равновесной цены p=2 имеем:
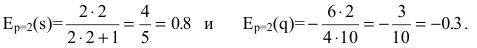 T.к. полученные значения эластичности по абсолютной величине меньше 1, то спрос и предложение данного товара при рыночной цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения. А именно, при увеличении цены на 1% спрос уменьшится на 0.3%, предложение увеличится на 0.8%.
T.к. полученные значения эластичности по абсолютной величине меньше 1, то спрос и предложение данного товара при рыночной цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения. А именно, при увеличении цены на 1% спрос уменьшится на 0.3%, предложение увеличится на 0.8%.
3) при увеличении цены на 5% относительно равновесной спрос уменьшится на 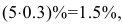 и, следовательно, доход возрастет на 3.5%.
и, следовательно, доход возрастет на 3.5%.
Пример №36
Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 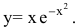 Требуется:
Требуется:
- 1) определить средние и предельные издержки при объеме продукции х=0.5 условных единиц;
- 2) найти эластичность издержек при выпуске продукции, равном
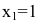 и
и 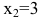 условных единиц.
условных единиц.
Решение:
1) функция средних издержек (на единицу продукции) выражается отношением 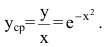 При х=0.25 средние издержки равны
При х=0.25 средние издержки равны
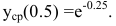
Функция предельных издержек выражается производной
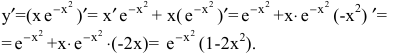
При х=0.5 предельные издержки составят
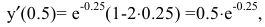 что вдвое меньше средних издержек.
что вдвое меньше средних издержек.
2) эластичность издержек у относительно объема выпускаемой продукции х рассчитывается по формуле:
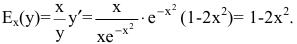
При 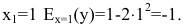 Это означает, что при увеличении количества произведенной продукции на 1% (с 1 до 1.01) издержки уменьшатся на 1%.
Это означает, что при увеличении количества произведенной продукции на 1% (с 1 до 1.01) издержки уменьшатся на 1%.
При 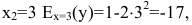 т.е. с увеличением количества произведенной продукции на 1% (с 3 до 3.01) затраты уменьшатся на 17%.
т.е. с увеличением количества произведенной продукции на 1% (с 3 до 3.01) затраты уменьшатся на 17%.
Уравнение нормали к плоской кривой
Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. Если касательная в точке 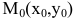 к графику непрерывной функции y=f(x) имеет вид
к графику непрерывной функции y=f(x) имеет вид 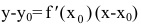 (см. п. 4.1), то перпендикулярная к ней прямая имеет угловой коэффициент
(см. п. 4.1), то перпендикулярная к ней прямая имеет угловой коэффициент 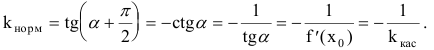 Таким образом, при
Таким образом, при 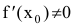 уравнение нормали в точке
уравнение нормали в точке 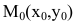 имеет вид
имеет вид 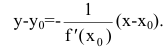 Если же
Если же 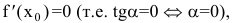 то нормаль параллельна оси Оу:
то нормаль параллельна оси Оу: 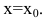
Пример №37
Показать, что для гиперболы ху=-1 площадь треугольника, образованного координатными осями и касательной в точке А(-1,1), равна квадрату полуоси гиперболы.
Решение:
В общем курсе аналитической геометрии давалось каноническое уравнение гиперболы. «Школьная» гипербола ху=а получается из уравнения 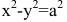 преобразованием поворота, которое нашей программой не предусмотрено. Полуось гиперболы определим как расстояние между вершиной и центром симметрии гиперболы. Очевидно, вершины гиперболы ху=-1 находятся в точках А(-1,1) и В( 1 ,-1), а центр симметрии совпадает с началом координат. Тогда полуось гиперболы равна
преобразованием поворота, которое нашей программой не предусмотрено. Полуось гиперболы определим как расстояние между вершиной и центром симметрии гиперболы. Очевидно, вершины гиперболы ху=-1 находятся в точках А(-1,1) и В( 1 ,-1), а центр симметрии совпадает с началом координат. Тогда полуось гиперболы равна 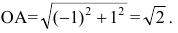 Следовательно, квадрат полуоси гиперболы равен 2.
Следовательно, квадрат полуоси гиперболы равен 2.
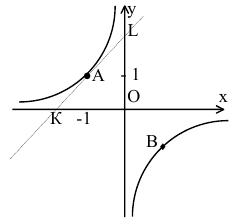
Составим уравнение касательной к гиперболе ху=-1 в вершине А(-1,1). Общее уравнение касательной к кривой y=f(x) в точке 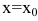 имеет вид:
имеет вид:
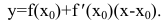
В нашем случае 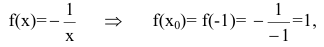
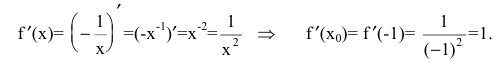
Искомое уравнение касательной имеет вид:

Найдем точки пересечения касательной с осями координат:

Тогда треугольник, образованный координатными осями и касательной, будет иметь вершины О(0,0), К(-2,0) и L(0,2). Т.к. треугольник прямоугольный, то его площадь равна
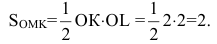
2=2. Задача решена.
Производные высших порядков
До сих пор мы рассматривали производную y'=f'(x) от функции y=f(x), называемую производной первого порядка. По производная y'=f'(x) сама является функцией, которая также может иметь производную. Производной второго порядка называется производная от производной первого порядка (у')' и обозначается 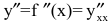 и т.д. В общем случае, производной n-го порядка называется производная от производной (n-l)-гo порядка (для обозначения производных выше третьего порядка используются арабские цифры в скобках):
и т.д. В общем случае, производной n-го порядка называется производная от производной (n-l)-гo порядка (для обозначения производных выше третьего порядка используются арабские цифры в скобках): 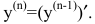
Ранее было установлено, что если точка движется прямолинейно по закону s=s(t) (где s - путь, t - время), то 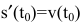 представляет скорость изменения пути в момент
представляет скорость изменения пути в момент 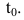 Следовательно, ускорение точки в момент
Следовательно, ускорение точки в момент 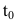 есть вторая производная пути по времени:
есть вторая производная пути по времени:
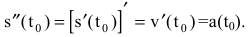
В этом состоит механический смысл второй производной.
Пример №38
Известно, что траекторией брошенного камня является парабола. Найти его скорость и ускорение.
Решение:
Запишем уравнение траектории брошенного камня 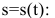
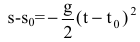 - парабола с вершиной в точке
- парабола с вершиной в точке 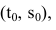 ветви которой направлены вниз, g - гравитационная постоянная. Тогда
ветви которой направлены вниз, g - гравитационная постоянная. Тогда 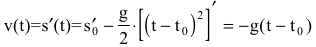 - скорость камня;
- скорость камня; 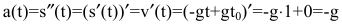 - его ускорение, что согласуется с известным физическим законом: всякое брошенное тело испытывает постоянное ускорение свободного падения.
- его ускорение, что согласуется с известным физическим законом: всякое брошенное тело испытывает постоянное ускорение свободного падения.
Производная неявной функции
Выше было рассмотрено дифференцирование явных функций, заданных формулой y=f(x), правая часть которых не содержала зависимой переменной. Если же функция y=f(x) задана уравнением F(x,y)=0, не разрешенным относительно зависимой переменной, то говорят, что функция у задана неявно.
Внимание! Не всякое уравнение F(x,y)=0 определяет неявную функцию. Например, уравнение 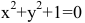 в действительной области не определяет никакой функции. Иногда одно уравнение такого вида может определять несколько функций. Например, уравнение
в действительной области не определяет никакой функции. Иногда одно уравнение такого вида может определять несколько функций. Например, уравнение 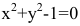 определяет две функции:
определяет две функции: 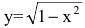 и
и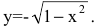
Часто разрешить уравнение F(x,y)=0 относительно переменной затруднительно. В таком случае функцию приходится изучать, пользуясь непосредственно уравнением, определяющим ее. Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y)=0.
Для нахождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х. Затем из полученного уравнения найти производную у'.
Пример №39
Покажите, что функция y=f(x), заданная неявно выражением 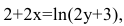 удовлетворяет уравнению
удовлетворяет уравнению 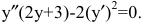
Решение:
Найдем первую производную данной функции. Для этого продифференцируем обе части уравнения 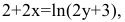 используя формулы и правила дифференцирования:
используя формулы и правила дифференцирования:
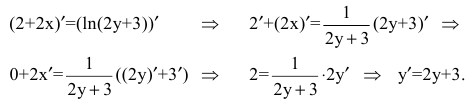
Найдем вторую производную:
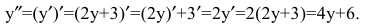
Подставим найденные выражения в дифференциальное уравнение: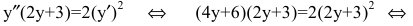
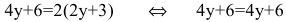 - верное тождество.
- верное тождество.
Правило Лопиталя
С помощью производной можно находить многие пределы. Следующее утверждение позволит свести предел отношения двух функций с случае неопределенностей вида 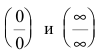 к пределу отношения производных, который очень часто вычисляется проще.
к пределу отношения производных, который очень часто вычисляется проще.
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если этот предел существует:
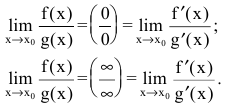
Внимание! В правой части формул берется отношение производных, а не производная отношения.
Пример №40
Вычислить предел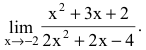
Решение:
Имеем неопределенность вида 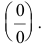 Т.к. числитель и знаменатель дроби непрерывны и дифференцируемы, то можно применить правило Лопиталя:
Т.к. числитель и знаменатель дроби непрерывны и дифференцируемы, то можно применить правило Лопиталя: 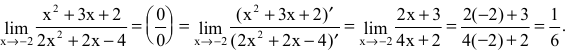
Замечание. Правило Лопиталя можно применять повторно, если вновь приходим к соотношению неопределенностей вида 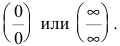
Пример №41
Вычислить предел 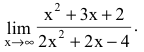
Решение:
Числитель и знаменатель дроби непрерывны, дифференцируемы и стремятся к бесконечности. Следовательно, можно применить правило Лопиталя (в данном примере мы воспользовались им дважды):
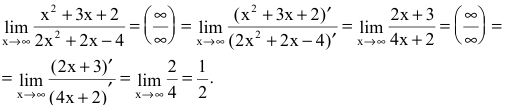
Замечание. Другие неопределенности раскрываются по правилу Лопиталя, если их предварительно свести к основному виду 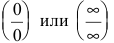 с помощью тождественных преобразований.
с помощью тождественных преобразований.
Пример №42
Найти 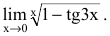
Решение:
Преобразуя выражение и используя непрерывность показательной функции, получим:
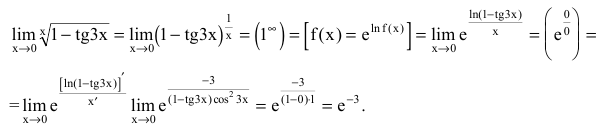
Оптимизация (процесс нахождения экстремума максимума или минимума экономических функций)
В этом параграфе оптимизацию будем понимать как процесс нахождения экстремума (максимума или минимума) экономических функций, т.е. выбор наилучшего варианта из множества возможных. Говорят, что в точке  функция y=f(x) имеет (локальный) максимум, если существует такая окрестность точки
функция y=f(x) имеет (локальный) максимум, если существует такая окрестность точки 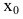 , что для всех х из этой окрестности выполнено условие
, что для всех х из этой окрестности выполнено условие 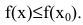 Аналогично, функция y=f(x) в точке
Аналогично, функция y=f(x) в точке 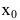 имеет (локальный) минимум, если существует такая окрестность точки
имеет (локальный) минимум, если существует такая окрестность точки 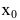 , что для всех х из этой окрестности выполнено условие
, что для всех х из этой окрестности выполнено условие 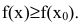 Точки (локальных) максимума и минимума называются точками (локального) экстремума, а значение функции в них - (локальными) экстремумами функции.
Точки (локальных) максимума и минимума называются точками (локального) экстремума, а значение функции в них - (локальными) экстремумами функции.
Внимание! Не следует путать понятие локального экстремума функции с ее наибольшим или наименьшим значением (так называемым глобальным максимумом или минимумом). Па одном промежутке функция может иметь несколько экстремумов, причем минимум может оказаться больше максимума подобно тому, как впадина в горах может иметь большую отметку над уровнем моря, чем невысокая вершина. А наибольшее и наименьшее значение непрерывной на отрезке функции может достигаться как в точках экстремума, так и на концах отрезка.
Геометрически в точке экстремума касательная к графику функции либо горизонтальна, либо не существует. Следовательно, непрерывная функция может иметь экстремум лишь в тех точках, где производная функции равна нулю или не существует (необходимое условие экстремума). Точки, в которых выполнено необходимое условие экстремума, называются критическими. (Иногда точки, в которых производная обращается в нуль, называют стационарными.)
Замечание Критическая точка не обязательно является точкой экстремума. Это лишь точка возможного экстремума функции.
Достаточное условие экстремума. Если в критической точке вторая производная положительна, то это точка минимума, а если отрицательна - точка максимума.
Для запоминания этой теоремы предлагаем мнемоническое правило: если плюс - котелок наполняется, если минус - опустошается.

Пример №43
Пусть в краткосрочном плане производственная функция зависит только от численности персонала и имеет вид
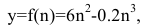
где у - выпуск продукции, а n- число работающих. Определить численность персонала, при которой выпуск у достигает максимального значения.
Решение:
Выпуск продукции y=f(n) - функция натурального аргумента. Для решения задачи рассмотрим обобщенную функцию действительного аргумента 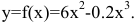 Новая функция везде непрерывна и дифференцируема. Найдем стационарные точки, для чего вычислим производную и приравняем ее к нулю:
Новая функция везде непрерывна и дифференцируема. Найдем стационарные точки, для чего вычислим производную и приравняем ее к нулю:
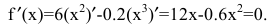 .
.
Решая квадратное уравнение, легко находим 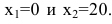 Вычисляем вторую производную:
Вычисляем вторую производную:
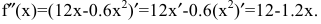
При 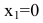 имеем
имеем
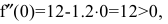
следовательно, в данной точке имеется минимум. Это естественно, т.к. нет выпуска продукции, если нет рабочих. Для второй точки
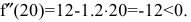
Поэтому в точке 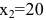 максимум. Соответствующий выпуск продукции
максимум. Соответствующий выпуск продукции 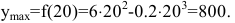
Исследование функции на монотонность
С помощью производной можно найти промежутки возрастания и убывания функции. Функция y=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции:
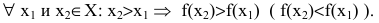
Возрастающие и убывающие функции называются монотонными.
Достаточное условие монотонности. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она возрастает (убывает) на этом промежутке:
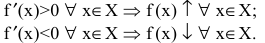
Таким образом, если при переходе через критическую точку производная дифференцируемой функции меняет знак с плюса на минус, то это точка (локального) максимума, а если с минуса на плюс - точка (локального) минимума (достаточное условие экстремума):
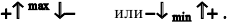
Если изменение знака производной не происходит, то экстремума нет.
Пример. Исследовать функцию 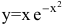 на монотонность.
на монотонность.
Решение. Область определения функции 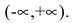 С помощью первой производной найдем точки возможного экстремума:
С помощью первой производной найдем точки возможного экстремума:
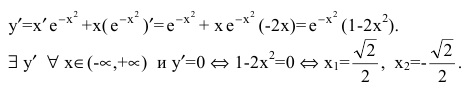
Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в таблице.
Итак, функция убывает на интервалах 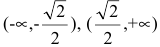 и возрастает на
и возрастает на 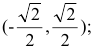 в точке
в точке 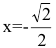 имеем минимум:
имеем минимум: 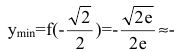 0.43
0.43
а 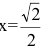 точка максимума:
точка максимума: 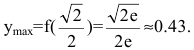
Выпуклость и вогнутость графика функции
Точки перегиба
График дифференцируемой функции y=f(x) называется выпуклым (выпуклым вверх) в точке 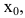 если он расположен ниже касательной в некоторой окрестности этой точки. Аналогично, график дифференцируемой функции y=f(x) называется вогнутым (выпуклым вниз) в точке
если он расположен ниже касательной в некоторой окрестности этой точки. Аналогично, график дифференцируемой функции y=f(x) называется вогнутым (выпуклым вниз) в точке 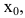 если он расположен выше касательной в некоторой окрестности этой точки. Однако могут существовать точки, слева от которых в некоторой в достаточно малой окрестности график лежит по одну сторону от касательной, а справа - по другую. Точки графика, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба.
если он расположен выше касательной в некоторой окрестности этой точки. Однако могут существовать точки, слева от которых в некоторой в достаточно малой окрестности график лежит по одну сторону от касательной, а справа - по другую. Точки графика, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба.
Достаточное условие направления выпуклости. Если вторая производная дважды дифференцируемой функции отрицательна (положительна') внутри некоторого промежутка, то функция выпукла (вогнута) на этом промежутке:
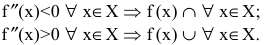
Следовательно, если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то это точка перегиба (достаточное условие перегиба):
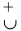 точка перегиба
точка перегиба 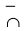 или
или  точка перегиба
точка перегиба 
Отсюда вытекает необходимое условие перегиба: вторая производная дважды дифференцируемой функции в точке перегиба равна нулю или не существует.
Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то это точка перегиба.
Пример №44
Исследовать функцию 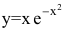 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.
Решение:
Область определения функции 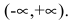 С помощью второй производной найдем точки возможного перегиба:
С помощью второй производной найдем точки возможного перегиба:
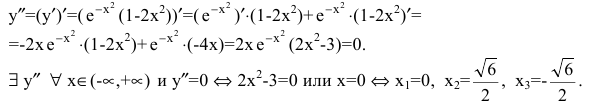
Эти точки разбивают область определения функции на интервалы, в которых сохраняется направление выпуклости или вогнутости. Результаты удобно представить в таблице.
Кривая, изображающая график функции, выпукла на интервалах 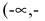
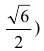 и
и 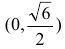 и вогнута на интервалах
и вогнута на интервалах 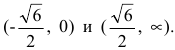 В точках
В точках 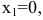
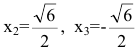 имеем перегиб:
имеем перегиб:
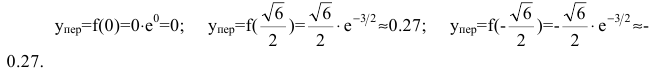
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |