
Дифференциальная геометрия - определение и вычисление с примерами решения
Содержание:
Дифференциальная геометрия и дифференциальная топология — два смежных раздела математики, которые изучают гладкие многообразия, обычно с дополнительными структурами. Они находят множество применений в физике, особенно в общей теории относительности.
Определения
Определение 6.1. Вектор-функцией в трёхмерном пространстве векторов 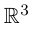
Если аргумент вектор-функции обозначить через 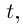 то вектор-функцию можно записать как
то вектор-функцию можно записать как 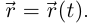
В дальнейшем мы будем рассматривать трёхмерный случай, но везде, где не упоминаются векторное и смешанное произведения векторов, все без изменений сохраняется для двумерного случая.
Если в 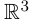 задан базис
задан базис 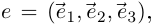 то вектор-функцию можно представить координатами в этом базисе; при этом будем употреблять запись
то вектор-функцию можно представить координатами в этом базисе; при этом будем употреблять запись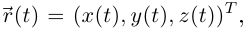 где
где 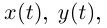
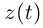 — обычные числовые («скалярные») функции. Напомним, что в линейной алгебре вектор представляется столбцом его координат в некотором базисе. Запись столбца координат нам сейчас неудобна, поэтому будем записывать строку с последующим транспонированием
— обычные числовые («скалярные») функции. Напомним, что в линейной алгебре вектор представляется столбцом его координат в некотором базисе. Запись столбца координат нам сейчас неудобна, поэтому будем записывать строку с последующим транспонированием 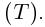 Если в другом базисе
Если в другом базисе 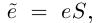 где
где  — матрица перехода от базиса
— матрица перехода от базиса к базису
к базису 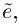 эта же вектор-функция имеет координатный столбец
эта же вектор-функция имеет координатный столбец 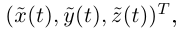 то
то
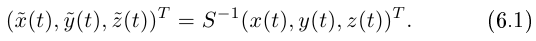
Определение 6.2. Говорят, что 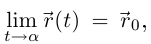 где
где 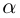 — один из 6 СПС, если в некотором базисе
— один из 6 СПС, если в некотором базисе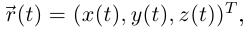
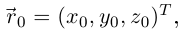 и
и
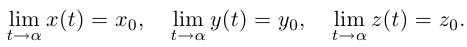
Определение 6.3. Вектор-функция 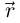 называется непрерывной в точке
называется непрерывной в точке 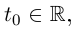 если существует
если существует 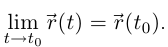
Определение 6.4. Пусть 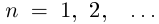 Если вектор-функция
Если вектор-функция 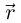 имеет в некотором базисе координатный столбец
имеет в некотором базисе координатный столбец 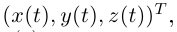 причём существуют конечные
причём существуют конечные 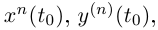
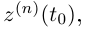 то вектор, имеющий в том же базисе координатный столбец
то вектор, имеющий в том же базисе координатный столбец 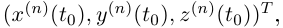 называется
называется  производной вектор-функции
производной вектор-функции 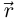 в точке
в точке  применяется обозначение
применяется обозначение 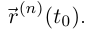 В этом случае вектор-функция
В этом случае вектор-функция 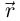 называется
называется 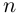 раз дифференцируемой в точке
раз дифференцируемой в точке 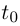 (дифференцируемой при
(дифференцируемой при 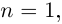 дважды дифференцируемой при
дважды дифференцируемой при 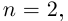 и т.д.).
и т.д.).
Замечание:
Определения 6.2 и 6.4 формально зависят от выбора базиса. Покажем, что определение 6.4 даст тот же вектор 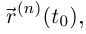 если выбрать другой базис
если выбрать другой базис 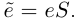 Если функции
Если функции 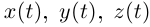 имеют конечную
имеют конечную 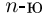 производную в точке
производную в точке 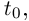 то из (6.1) следует, что то же можно сказать про функции
то из (6.1) следует, что то же можно сказать про функции 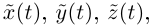 причём
причём
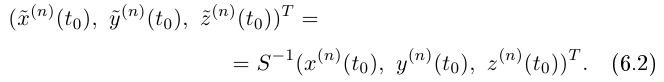
Таким образом, координатный столбец вектора 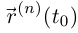 по определению 6.4 в базисе
по определению 6.4 в базисе 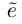 (левая часть 6.2) получается из координатного столбца этого же вектора по определению 6.4 в базисе е (в правой части (6.2)) по обычным формулам перехода от базиса е к базису
(левая часть 6.2) получается из координатного столбца этого же вектора по определению 6.4 в базисе е (в правой части (6.2)) по обычным формулам перехода от базиса е к базису 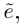 что означает независимость определения 6.4 от выбора базиса. Аналогично можно доказать независимость от выбора базиса определения 6.2.
что означает независимость определения 6.4 от выбора базиса. Аналогично можно доказать независимость от выбора базиса определения 6.2.
Лемма 6.1. Если числовые функции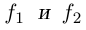 и вектор-функции
и вектор-функции 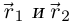 непрерывны в точке
непрерывны в точке 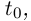 то в этой точке непрерывны также следующие функции (скалярные и векторные):
то в этой точке непрерывны также следующие функции (скалярные и векторные):
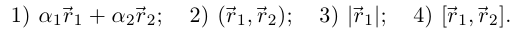
Докажем, например, утверждение 4). В силу замечания о независимости определения 6.2 от выбора базиса, достаточно доказать непрерывность всех координатных функций вектор-функции 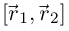 в некотором ортонормированием правом базисе
в некотором ортонормированием правом базисе 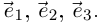 Но в этом базисе
Но в этом базисе
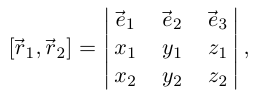
И все координатные функции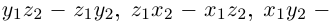
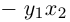 непрерывны в точке
непрерывны в точке 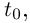 значит, непрерывной является и вектор-функция
значит, непрерывной является и вектор-функция 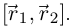
Лемма 6.2. Если числовые функции 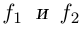 и вектор-функции
и вектор-функции 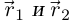 дифференцируемы в точке
дифференцируемы в точке 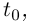 то в этой точке:
то в этой точке:
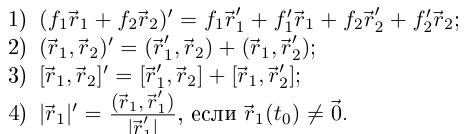
2) В координатах в ортонормированном базисе 
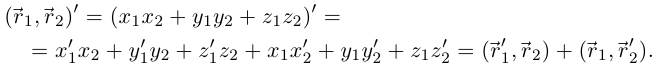
Утверждения 1) и 3) доказываются аналогично.
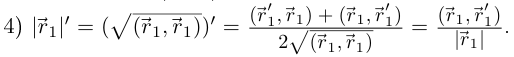
Лемма 6.3. Если вектор-функция 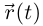 дифференцируема в точке
дифференцируема в точке 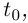 то
то
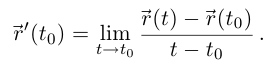
Соответствующее равенство справедливо для всех координатных функций, значит, и для вектор-функции.
Определение 6.5. Числовая функция 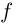 называется непрерывно дифференцируемой на промежутке I, если она дифференцируема на I. а сё производная
называется непрерывно дифференцируемой на промежутке I, если она дифференцируема на I. а сё производная 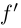 , дополненная соответствующими значениями односторонних производных в концах I (если они принадлежат I), непрерывна на этом промежутке (см. определения 4.8 и 3.10).
, дополненная соответствующими значениями односторонних производных в концах I (если они принадлежат I), непрерывна на этом промежутке (см. определения 4.8 и 3.10).
Определение 6.6. Числовая функция 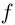 называется дважды дифференцируемой на промежутке I, если во всех внутренних точках I существует конечная
называется дважды дифференцируемой на промежутке I, если во всех внутренних точках I существует конечная 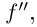 а в концах промежутка (если они ему принадлежат)
а в концах промежутка (если они ему принадлежат) 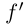 имеет соответствующие односторонние производные. При этом под значениями
имеет соответствующие односторонние производные. При этом под значениями 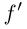 в концах промежутка понимаются соответствующие односторонние производные. Например, для отрезка
в концах промежутка понимаются соответствующие односторонние производные. Например, для отрезка 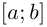
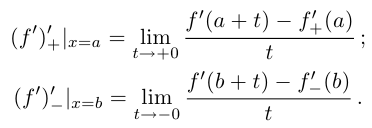
Аналогично дастся определение трижды и т.д. дифференцируемой (функции на промежутке I.
Определение 6.7. Вектор-функция 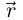 называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) на промежутке I, если таковыми же являются все её координатные функции в некотором базисе.
называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) на промежутке I, если таковыми же являются все её координатные функции в некотором базисе.
Аналогично определениям 6.2 и 6.4, определение 6.7 не зависит от выбора базиса.
Отметим, что для вектор-функций теорема Лагранжа, вообще говоря, неверна. Например, пусть в ортонормированном базисе в  вектор-функция имеет координатный столбец
вектор-функция имеет координатный столбец 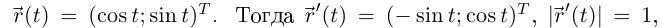
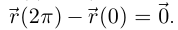 Поэтому равенство
Поэтому равенство 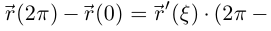
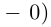 невозможно ни при каком значении
невозможно ни при каком значении 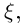 так как модуль вектора в правой части этого равенства при любом
так как модуль вектора в правой части этого равенства при любом 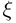 равен
равен 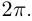
Лемма 6.4 (заменитель теоремы Лагранжа для вектор-функций). Если вектор-функция 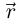 непрерывна на
непрерывна на 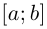 и дифференцируема на
и дифференцируема на 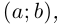 то существует точка
то существует точка 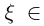
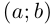 такая, что
такая, что
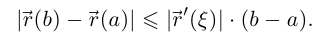
Рассмотрим числовую функцию 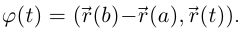 По леммам 6.1 и 6.2 она непрерывна на
По леммам 6.1 и 6.2 она непрерывна на 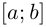 и дифференцируема на
и дифференцируема на 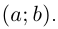 Тогда по теореме Лагранжа существует точка
Тогда по теореме Лагранжа существует точка 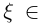
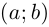 такая, что
такая, что 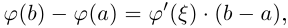 т.е.
т.е.
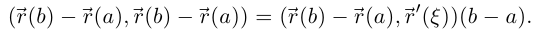
Так как для любых векторов 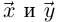 выполняется неравенство
выполняется неравенство
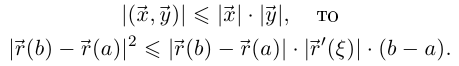
Если 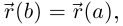 то лемма верна для любого значения
то лемма верна для любого значения 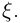 Если
Если 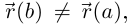 то из последнего неравенства получаем:
то из последнего неравенства получаем: 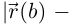
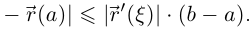
Для числовых функций во многих случаях фактически применяется не сама теорема Лагранжа, а лишь неравенство, аналогичное только что доказанному. Для вектор-функций ничего другого мы не имеем.
Кривые в пространстве
Аналогично определению 4.3 кривой на плоскости, дастся определение кривой в трёхмерном пространстве.
Определение 6.8. Пусть 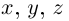 — три функции переменной
— три функции переменной 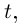 где
где 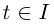 (I — некоторый промежуток). Тогда множество точек пространства
(I — некоторый промежуток). Тогда множество точек пространства 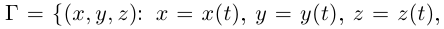
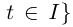 называется кривой в пространстве (если не оговорено противное, координаты точек рассматриваются в прямоугольной правой системе координат). Кривая Г называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.), если таковой же является вектор-функция
называется кривой в пространстве (если не оговорено противное, координаты точек рассматриваются в прямоугольной правой системе координат). Кривая Г называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.), если таковой же является вектор-функция 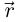 с координатным столбцом
с координатным столбцом 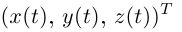 на промежутке I.
на промежутке I.
Следует отметить, что во многих курсах дифференциальной геометрии под кривой понимают не множество точек Г, а отображение 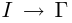 по закону
по закону 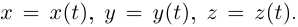 Для множества точек Г применяют другие названия, например, «носитель кривой». Мы не будем усложнять изложение основ дифференциальной геометрии кривых такими тонкостями.
Для множества точек Г применяют другие названия, например, «носитель кривой». Мы не будем усложнять изложение основ дифференциальной геометрии кривых такими тонкостями.
Кривую в пространстве можно рассматривать как множество концов векторов для данной вектор-функции 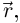 начала которых помещены в начало координат («годограф вектор-функции»
начала которых помещены в начало координат («годограф вектор-функции» 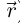 ). Физический смысл — траектория движущейся точки (
). Физический смысл — траектория движущейся точки (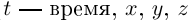 — координаты точки в момент t).
— координаты точки в момент t).
Определение 6.9. Кривая Г называется простой, если соответствие между I и Г, осуществляемое функцией 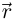 , является взаимно однозначным.
, является взаимно однозначным.
Кривую можно записать в векторном виде:
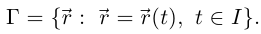
Пусть 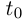 — внутренняя точка
— внутренняя точка 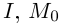 — точка кривой, соответствующая значению параметра
— точка кривой, соответствующая значению параметра 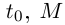 — точка, соответствующая значению параметра
— точка, соответствующая значению параметра 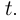 Если кривая простая, то при
Если кривая простая, то при 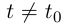 точки
точки 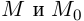 не совпадают. Проведём через точки
не совпадают. Проведём через точки 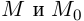 прямую (хорда кривой). Она имеет направляющий вектор
прямую (хорда кривой). Она имеет направляющий вектор 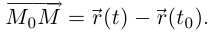
Определение 6.10. Пусть 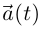 — единичный направляющий вектор хорды простой кривой
— единичный направляющий вектор хорды простой кривой 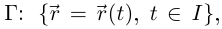 проходящей через точки
проходящей через точки  направленный в сторону возрастания t (от
направленный в сторону возрастания t (от  если
если  и от
и от 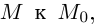 если
если 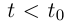 ); здесь
); здесь 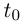 — внутренняя точка промежутка I. Если существует
— внутренняя точка промежутка I. Если существует 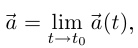 то прямая с направляющим вектором
то прямая с направляющим вектором  проходящая через точку
проходящая через точку  называется касательной к кривой Г в точке
называется касательной к кривой Г в точке  (см. рис. 6.1)
(см. рис. 6.1)
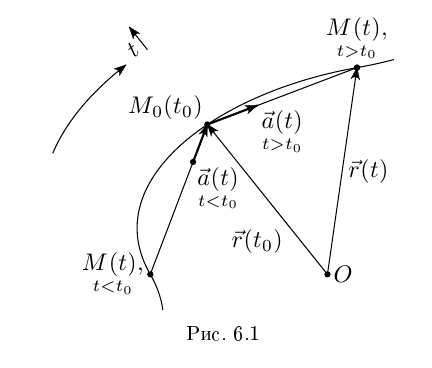
Касательную интуитивно можно представить как «предельное положение» хорды при 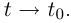
Отмстим, что вектор 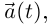 введённый в определении 6.10, определяется равенством
введённый в определении 6.10, определяется равенством
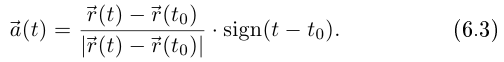
Теорема 6.1. Если для простой кривой Г: 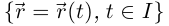 существует
существует 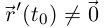 но внутренней точке
но внутренней точке 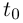 промежутка I, то кривая имеет касательную в точке, соответствующей значению параметра
промежутка I, то кривая имеет касательную в точке, соответствующей значению параметра 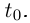 Вектор
Вектор 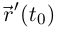 является направляющим вектором касательной, направленным в сторону возрастания t.
является направляющим вектором касательной, направленным в сторону возрастания t.
Равенство (6.3) можно переписать в виде
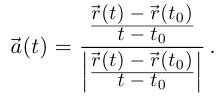
Так как по лемме 6.3 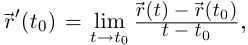 то по лемме 6.1
то по лемме 6.1 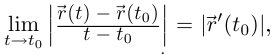 и если
и если 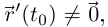 то существует
то существует 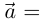
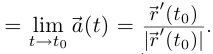 Так как вектор
Так как вектор 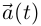 направлен в сторону возрастания t, то это же можно сказать и о «предельном» векторе
направлен в сторону возрастания t, то это же можно сказать и о «предельном» векторе 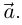 Векторы же
Векторы же 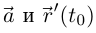 одинаково направлены.
одинаково направлены.
Пример №1
Рассмотрим дугу окружности 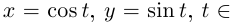
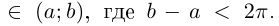 Это — простая кривая, и вектор
Это — простая кривая, и вектор 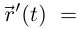
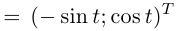 направлен по касательной к окружности против часовой стрелки (в сторону возрастания t); так как
направлен по касательной к окружности против часовой стрелки (в сторону возрастания t); так как 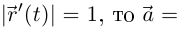
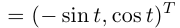 (см. рис. 6.2).
(см. рис. 6.2).
Физический смысл: если точка описывает траекторию 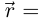
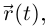 то вектор мгновенной скорости в момент направлен по касательной к кривой в точке
то вектор мгновенной скорости в момент направлен по касательной к кривой в точке 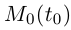 в сторону возрастания t.
в сторону возрастания t.
Отмстим, что если дифференцируемая кривая на плоскости задаётся уравнением 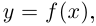 то её можно параметризовать так:
то её можно параметризовать так: 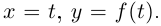 Направляющий вектор касательной имеет координатный столбец
Направляющий вектор касательной имеет координатный столбец 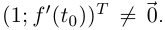 Касательная к этой кривой в смысле определения 4.5 (определение касательной к графику функции
Касательная к этой кривой в смысле определения 4.5 (определение касательной к графику функции 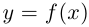 ) имеет угловой коэффициент
) имеет угловой коэффициент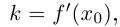 т.е. тот же направляющий вектор.
т.е. тот же направляющий вектор.
Определение 6.11. Кривая Г: 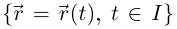 называется гладкой, если она непрерывно дифференцируема на I и
называется гладкой, если она непрерывно дифференцируема на I и 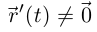 при всех
при всех 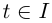 (в концах I рассматриваются односторонние производные, определяемые как векторы, координаты которых — соответствующие односторонние производные координатных функций).
(в концах I рассматриваются односторонние производные, определяемые как векторы, координаты которых — соответствующие односторонние производные координатных функций).
Замечание:
Если 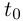 — конец I, принадлежащий этому промежутку, то аналогично определяется соответствующая односторонняя касательная к кривой и доказывается аналог теоремы 6.1 для односторонней производной
— конец I, принадлежащий этому промежутку, то аналогично определяется соответствующая односторонняя касательная к кривой и доказывается аналог теоремы 6.1 для односторонней производной 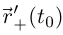 или
или 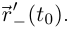
Гладкая кривая в любой точке имеет касательную, векторное уравнение которой 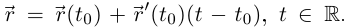 Непрерывно дифференцируемая кривая, имеющая в любой точке касательную, не обязана быть гладкой в смысле определения 6.11. Так, парабола
Непрерывно дифференцируемая кривая, имеющая в любой точке касательную, не обязана быть гладкой в смысле определения 6.11. Так, парабола 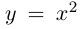 на плоскости, имеющая касательную в каждой точке, может быть параметризована следующим образом:
на плоскости, имеющая касательную в каждой точке, может быть параметризована следующим образом: 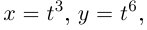 при этом в точке
при этом в точке 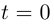 вектор
вектор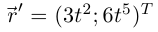 — нулевой и кривая не является гладкой.
— нулевой и кривая не является гладкой.
В определении касательной 6.10 вектор 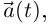 хотя он и выражается через параметр, имеет чисто геометрическую природу, при другой параметризации кривой он может разве что измениться на противоположный.
хотя он и выражается через параметр, имеет чисто геометрическую природу, при другой параметризации кривой он может разве что измениться на противоположный.
Поэтому касательная не зависит от параметризации кривой. Но если одна и та же кривая (как множество точек на плоскости или в пространстве) задастся по разному параметрическими уравнениями, то при одной параметризации она может быть гладкой, а при другой — нет.
Пример №2
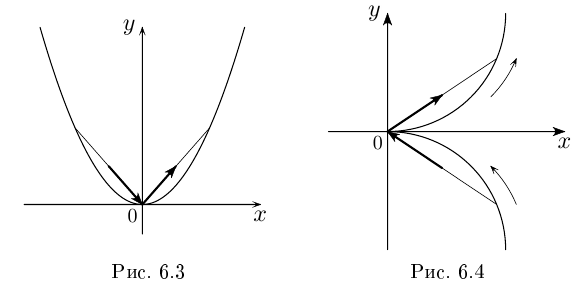
Рассмотрим кривую 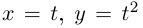 на плоскости. Это — парабола
на плоскости. Это — парабола 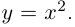 Производная вектор-функции
Производная вектор-функции 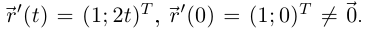 Кривая является гладкой, она в точке
Кривая является гладкой, она в точке 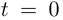 имеет касательную с направляющим вектором
имеет касательную с направляющим вектором 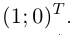 Это понятно и из геометрического определения (см. рис. 6.3). Ясно, что единичный вектор
Это понятно и из геометрического определения (см. рис. 6.3). Ясно, что единичный вектор 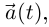 направленный в сторону возрастания t, имеет «предельное значение»
направленный в сторону возрастания t, имеет «предельное значение» 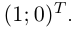 Кривая
Кривая 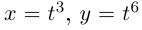 задаст ту же параболу, поэтому для нас опять-таки
задаст ту же параболу, поэтому для нас опять-таки 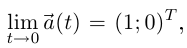 но гладкой она не является; как мы уже видели,
но гладкой она не является; как мы уже видели, 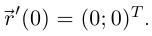
Пример №3
Рассмотрим кривую 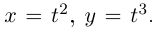 Она не является гладкой, так как
Она не является гладкой, так как 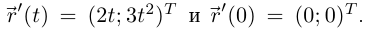 Касательной в точке
Касательной в точке 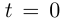 она не имеет, так как
она не имеет, так как 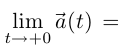
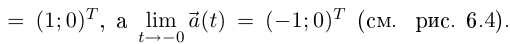 Есть только односторонние касательные (совпадающие) в этой точке, кривая имеет характерную форму клюва.
Есть только односторонние касательные (совпадающие) в этой точке, кривая имеет характерную форму клюва.
Определение 6.12. Пусть одна и та же кривая параметризуется двумя способами: 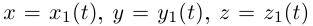 (т.е.
(т.е. 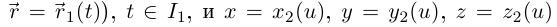 (т.е.
(т.е. 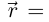
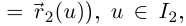 причём функция
причём функция 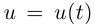 отображает промежуток
отображает промежуток 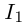 на множество
на множество 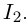 Если функция
Если функция 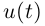 непрерывно дифференцируема на
непрерывно дифференцируема на 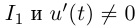 при всех
при всех 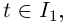 то функция
то функция 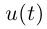 называется допустимой заменой параметра (ДЗП).
называется допустимой заменой параметра (ДЗП).
Лемма 6.5. При ДЗП простая непрерывно дифференцируемая кривая остаётся простой непрерывно дифференцируемой, гладкая кривая остаётся гладкой, касательная к кривой в данной точке не изменится.
Так как 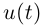 — непрерывная непостоянная функция на промежутке
— непрерывная непостоянная функция на промежутке 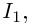 то из леммы 3.11 следует, что
то из леммы 3.11 следует, что 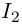 — также промежуток. Но
— также промежуток. Но 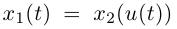 при всех
при всех 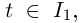 поэтому
поэтому 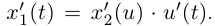 Аналогично,
Аналогично, 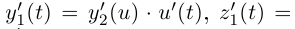
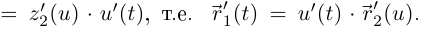 Значит, непрерывно дифференцируемая кривая остаётся непрерывно дифференцируемой, и, так как
Значит, непрерывно дифференцируемая кривая остаётся непрерывно дифференцируемой, и, так как 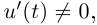 гладкая кривая остаётся гладкой.
гладкая кривая остаётся гладкой.
Функция 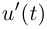 непрерывна и отлична от нуля на
непрерывна и отлична от нуля на 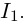 Значит, либо
Значит, либо 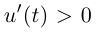 для всех
для всех 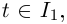 либо
либо 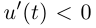 (если функция
(если функция 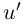 принимает два значения разного знака, то по теореме Больцано-Коши 3.13 найдётся точка, где
принимает два значения разного знака, то по теореме Больцано-Коши 3.13 найдётся точка, где 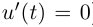 ). Поэтому по теореме 5.5 функция
). Поэтому по теореме 5.5 функция 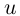 строго монотонна на
строго монотонна на 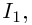 значит, она осуществляет взаимно однозначное соответствие между
значит, она осуществляет взаимно однозначное соответствие между 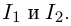 И если соответствие между
И если соответствие между 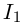 и Г было взаимно однозначным, то соответствие между
и Г было взаимно однозначным, то соответствие между 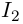 и Г также будет взаимно однозначным. Простая кривая остаётся простой.
и Г также будет взаимно однозначным. Простая кривая остаётся простой.
Наконец, рассмотрим некоторую точку кривой с радиусом-вектором 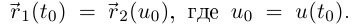 Так как
Так как 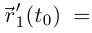
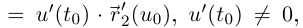 , то направляющие векторы касательной в двух параметризациях коллинеарны. Значит, касательная в фиксированной точке остаётся той же.
, то направляющие векторы касательной в двух параметризациях коллинеарны. Значит, касательная в фиксированной точке остаётся той же.
Пример №4
Рассмотрим верхнюю полуокружность единичной окружности 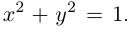 Её можно параметризовать двумя способами:
Её можно параметризовать двумя способами:
1)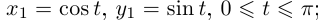
2)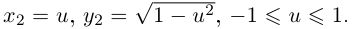
При этом 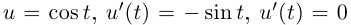 при
при 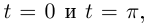 замена не является допустимой. А вот если
замена не является допустимой. А вот если 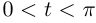 (соответственно
(соответственно 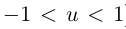 ), замена уже будет допустимой. Кстати, в первой параметризации
), замена уже будет допустимой. Кстати, в первой параметризации 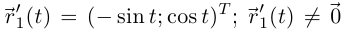 ни при одном значении
ни при одном значении 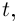 и кривая будет гладкой на любом промежутке изменения t.
и кривая будет гладкой на любом промежутке изменения t.
Так как 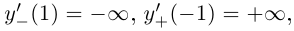 то во второй параметризации кривая не будет даже дифференцируемой на [-1; 1], но является гладкой на (—1; 1). Направляющий вектор касательной в точке кривой при
то во второй параметризации кривая не будет даже дифференцируемой на [-1; 1], но является гладкой на (—1; 1). Направляющий вектор касательной в точке кривой при 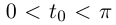 (или, что то же,
(или, что то же, 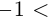
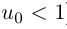 ) равен
) равен
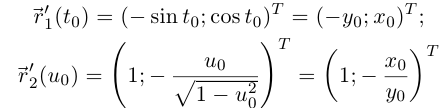
— векторы коллинеарны, но противоположно направлены. Это говорит о том, что при возрастании t и при возрастании 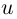 кривая пробегается в разные стороны (при возрастании t против часовой стрелки, т.е. налево по х, а при возрастании
кривая пробегается в разные стороны (при возрастании t против часовой стрелки, т.е. налево по х, а при возрастании 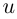 — направо по х).
— направо по х).
Определение 6.13. Кривая Г: 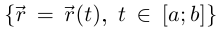 называется простой замкнутой, если она простая при
называется простой замкнутой, если она простая при 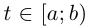 и
и 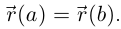
Например, окружность 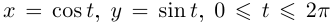 — простая замкнутая кривая.
— простая замкнутая кривая.
Длина кривой
Пусть 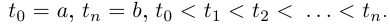 Рассмотрим на кривой Г:
Рассмотрим на кривой Г: 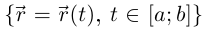 точки
точки 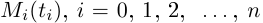 и построим из отрезков прямых
и построим из отрезков прямых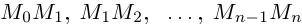 ломаную линию, вписанную в кривую Г. Длина её определяется как сумма длин входящих в неё отрезков. Если кривая не является простой, то возможно совпадение соседних точек
ломаную линию, вписанную в кривую Г. Длина её определяется как сумма длин входящих в неё отрезков. Если кривая не является простой, то возможно совпадение соседних точек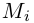 и
и 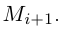 Тогда длина соответствующего отрезка равна 0.
Тогда длина соответствующего отрезка равна 0.
Определение 6.14. Длиной кривой Г: 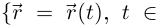
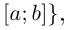 называется точная верхняя грань множества длин ломаных, вписанных в кривую Г. Если длина кривой конечна, то кривая называется спрямляемой.
называется точная верхняя грань множества длин ломаных, вписанных в кривую Г. Если длина кривой конечна, то кривая называется спрямляемой.
Будем обозначать длину кривой Г: 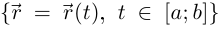 через
через 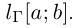
Лемма 6.6. Если 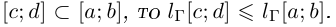 В частности, если кривая Г спрямляема при
В частности, если кривая Г спрямляема при 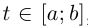 то она спрямляема и при
то она спрямляема и при 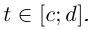
Пусть 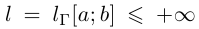 (т.е. либо конечна, либо бесконечна). Рассмотрим любую ломаную, вписанную в Г при
(т.е. либо конечна, либо бесконечна). Рассмотрим любую ломаную, вписанную в Г при 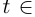
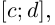 и продолжим её до ломаной, вписанной в Г при
и продолжим её до ломаной, вписанной в Г при 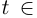
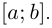 Длина меньшей ломаной не превосходит длины большей, следовательно, не превосходит
Длина меньшей ломаной не превосходит длины большей, следовательно, не превосходит 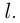 . Тогда и
. Тогда и 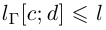 (как точная верхняя грань, см. лемму 1.3). Если
(как точная верхняя грань, см. лемму 1.3). Если 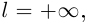 то доказывать нечего.
то доказывать нечего.
Лемма 6.7. Если кривая Г спрямляема при 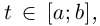 то при любом
то при любом 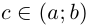 имеет место равенство
имеет место равенство
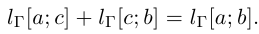
Спрямляемость Г при 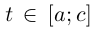 и при
и при 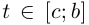 следует из леммы 6.6. Обозначим
следует из леммы 6.6. Обозначим 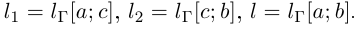
Рассмотрим произвольную ломаную 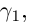 вписанную в Г при
вписанную в Г при 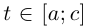 и произвольную ломаную
и произвольную ломаную 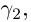 вписанную в Г при
вписанную в Г при 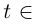
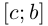 (см. рис. 6.5). Их объединение —ломаная
(см. рис. 6.5). Их объединение —ломаная 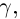 , вписанная в Г на
, вписанная в Г на 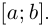 Так как
Так как 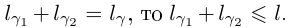 Зафиксируем ломаную
Зафиксируем ломаную 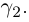 Переходя в последнем неравенстве к точной верхней грани по всем
Переходя в последнем неравенстве к точной верхней грани по всем 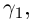 силу леммы 1.3 получим:
силу леммы 1.3 получим: 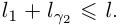 Переходя затем к точной верхней грани по
Переходя затем к точной верхней грани по 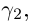 получим:
получим: 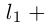
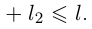
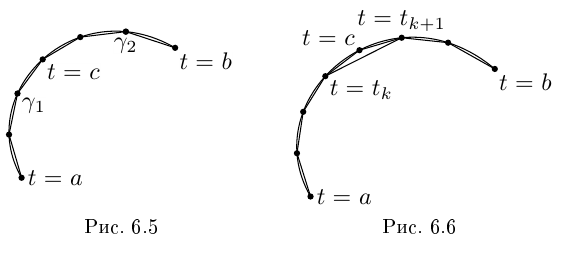
Рассмотрим теперь произвольную ломаную 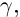 вписанную в Г. Если одна из её вершин соответствует значению параметра
вписанную в Г. Если одна из её вершин соответствует значению параметра  (как на рис. 6.5), то
(как на рис. 6.5), то  Если ни одна из вершин не соответствует
Если ни одна из вершин не соответствует 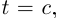 то существует номер
то существует номер 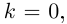
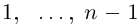 такой, что
такой, что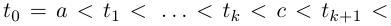
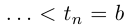 (вершины ломаной
(вершины ломаной 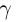 соответствуют значениям параметра
соответствуют значениям параметра 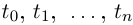 ). Рассмотрим ломаную
). Рассмотрим ломаную 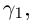 вписанную в Г при
вписанную в Г при 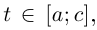 такую, что первые её
такую, что первые её 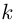 звеньев совпадают с первыми
звеньев совпадают с первыми 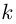 звеньями ломаной
звеньями ломаной 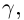 а последнее звено — отрезок, соединяющий точки, соответствующие
а последнее звено — отрезок, соединяющий точки, соответствующие 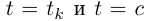 (см. рис. 6.6). Рассмотрим также ломаную
(см. рис. 6.6). Рассмотрим также ломаную 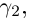 вписанную в Г при
вписанную в Г при 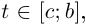 такую, что первое её звено — отрезок, соединяющий точки, соответствующие
такую, что первое её звено — отрезок, соединяющий точки, соответствующие 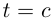 и
и 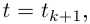 остальные совпадают с оставшимися звеньями
остальные совпадают с оставшимися звеньями 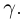 Тогда
Тогда 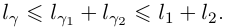 Итак, для любой ломаной
Итак, для любой ломаной 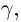 вписанной в данную кривую Г,
вписанной в данную кривую Г, 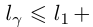
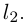 Переходя к точной верхней грани, получим:
Переходя к точной верхней грани, получим: 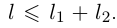 Получаем неравенства в обе стороны, значит,
Получаем неравенства в обе стороны, значит, 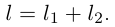
Замечание:
Если не требовать спрямляемость Г (т.е. 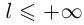 ), то лемма сохраняет силу.
), то лемма сохраняет силу.
Следствие. Если кривая Г спрямляема при 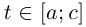 и
и 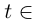
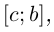 то она спрямляема и при
то она спрямляема и при 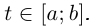
Лемма 6.8. Непрерывно дифференцируемая кривая Г = 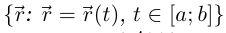 спрямляема, и её длина
спрямляема, и её длина 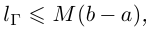 где
где 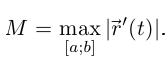
По лемме 6.1 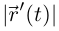 — непрерывная функция на
— непрерывная функция на 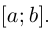 По теоремам 3.11 и 3.12 она ограничена и достигает своей точной верхней грани. Поэтому можно рассматривать
По теоремам 3.11 и 3.12 она ограничена и достигает своей точной верхней грани. Поэтому можно рассматривать 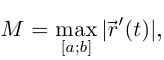
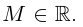
Длина любой ломаной, вписанной в кривую Г, равна

(здесь применена лемма 6.4, 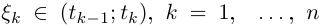 ).
).
Поэтому 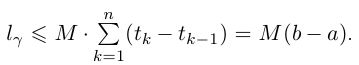 Переходя к точной fc=i
Переходя к точной fc=i
верхней грани, получим: 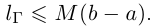
Теорема 6.2. Пусть кривая Г = 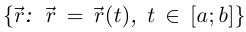 непрерывно дифференцируема, и
непрерывно дифференцируема, и 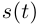 —длина той части кривой Г, которая соответствует изменению параметра от а до
—длина той части кривой Г, которая соответствует изменению параметра от а до 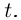 Тогда функция
Тогда функция 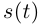 непрерывно дифференцируема на
непрерывно дифференцируема на 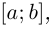 причем
причем 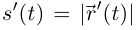 при всех
при всех 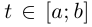 (в точках
(в точках 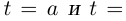
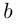 рассматриваются соответствующие односторонние производные).
рассматриваются соответствующие односторонние производные).
Из лемм 6.6, 6.7, 6.8 следует, что кривая Г спрямляема, функция 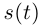 определена при всех
определена при всех 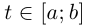 и возрастает на
и возрастает на 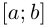 (вообще говоря, нестрого), причём если
(вообще говоря, нестрого), причём если 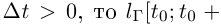
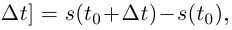 a если
a если 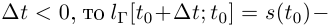
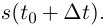 В любом случае длина кривой при
В любом случае длина кривой при 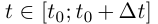 равна
равна 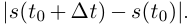 Длина отрезка, соединяющего концы кривой, не превосходит длины кривой, поэтому
Длина отрезка, соединяющего концы кривой, не превосходит длины кривой, поэтому
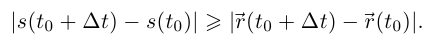
По лемме 6.8
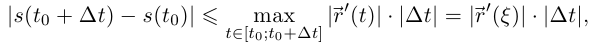
где 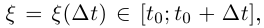 так как непрерывная на отрезке функция принимает наибольшее значение в некоторой точке отрезка. После деления всех частей двойного неравенства на
так как непрерывная на отрезке функция принимает наибольшее значение в некоторой точке отрезка. После деления всех частей двойного неравенства на 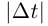 получим
получим
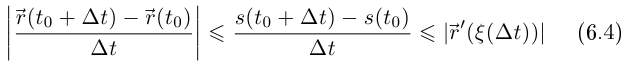
(здесь использовано то, что функция 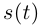 возрастает, и, следовательно, при любом знаке
возрастает, и, следовательно, при любом знаке 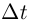 знак выражения
знак выражения 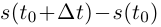 такой же). Далее,
такой же). Далее,
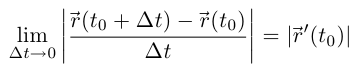
(в силу лемм 6.3 и 6.1). Так как 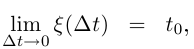 то по теореме 3.8, применённой к каждой из компонент вектора
то по теореме 3.8, применённой к каждой из компонент вектора 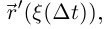 имеем:
имеем: 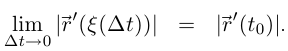 Тогда по теореме 3.4 из (6.4) следует, что существует
Тогда по теореме 3.4 из (6.4) следует, что существует 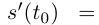
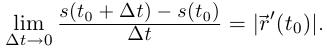
Замечание. Гладкость кривой в условии теоремы 6.2 не требуется.
Дифференциал функции 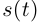 обычно называют дифференциалом дуги кривой
обычно называют дифференциалом дуги кривой 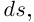 из теоремы 6.2 следует, что
из теоремы 6.2 следует, что 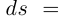
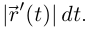
Вектор, компоненты которого — дифференциалы координатных функций вектор-функции 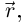 т.е. вектор
т.е. вектор
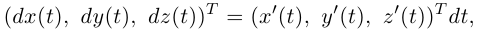
называют дифференциалом вектор-функции 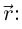
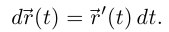
Тогда 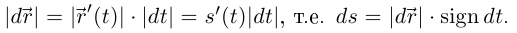
Если кривая не только непрерывно дифференцируема, но ещё и гладкая, то в каждой её точке 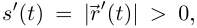 т.е. функция
т.е. функция 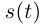 строго возрастает на
строго возрастает на 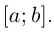 Тогда замена параметра
Тогда замена параметра 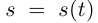 является ДЗП. На любой гладкой кривой можно ввести параметр, равный переменной длине дуги кривой (так называемый натуральный параметр). Уравнения кривой в такой параметризации называют натуральными уравнениями кривой. Обычно полагают
является ДЗП. На любой гладкой кривой можно ввести параметр, равный переменной длине дуги кривой (так называемый натуральный параметр). Уравнения кривой в такой параметризации называют натуральными уравнениями кривой. Обычно полагают 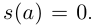 Можно положить
Можно положить 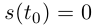 для некоторого другого значения
для некоторого другого значения 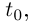 но если при этом
но если при этом 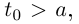 то возникнут оговорки о знаке
то возникнут оговорки о знаке 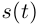 (при
(при 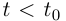 выполняется неравенство
выполняется неравенство 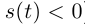 ).
).
Пример №5
Составить натуральные уравнения прямой линии 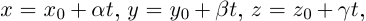 где
где 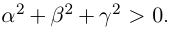
Так как 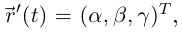 то
то 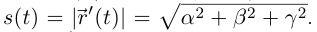 По следствию из теоремы 4.15
По следствию из теоремы 4.15 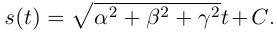 Если положить
Если положить 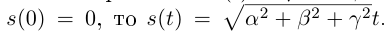 Натуральные уравнения прямой имеют вид
Натуральные уравнения прямой имеют вид
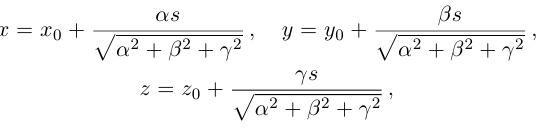
Пример №6
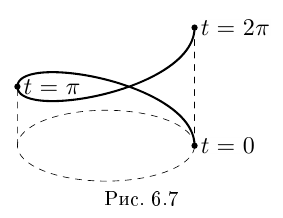
Составить натуральные уравнения винтовой линии 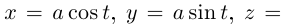
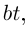 где
где 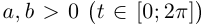 (cм. рис. 6.7).
(cм. рис. 6.7).
Так как 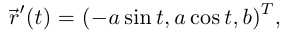 то
то 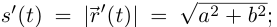 по следствию из теоремы 4.15:
по следствию из теоремы 4.15: 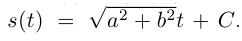 Если положить
Если положить 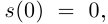 то
то 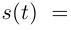
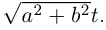 Натуральные уравнения винтовой линии имеют вид
Натуральные уравнения винтовой линии имеют вид
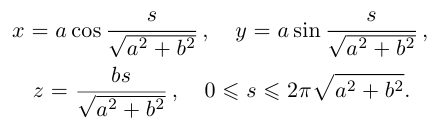
Пример №7
График непрерывно дифференцируемой функции 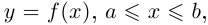 на плоскости можно параметризовать так:
на плоскости можно параметризовать так: 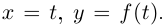 Тогда
Тогда 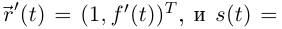
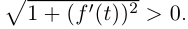 Натуральные уравнения можно написать явно, если известна функция, производная от которой равна
Натуральные уравнения можно написать явно, если известна функция, производная от которой равна 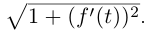
Дважды дифференцируемые гладкие кривые. Кривизна кривой
Определение 6.15. Пусть Г: 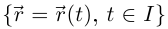 —дважды дифференцируемая гладкая кривая. Тогда кривизной кривой в точке с радиусом-вектором
—дважды дифференцируемая гладкая кривая. Тогда кривизной кривой в точке с радиусом-вектором 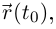 где
где 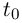 — внутренняя точка промежутка I, называется модуль вектора второй производной вектор-функции
— внутренняя точка промежутка I, называется модуль вектора второй производной вектор-функции 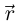 по натуральному параметру s при значении
по натуральному параметру s при значении 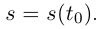
Производные по натуральному параметру принято обозначать точками (вместо штрихов). В этих обозначениях кривизна 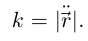
Лемма 6.9. Пусть Г: 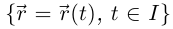 — дважды дифференцируемая гладкая кривая. Тогда для производных вектор-функции
— дважды дифференцируемая гладкая кривая. Тогда для производных вектор-функции 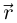 по натуральному параметру в точках, соответствующих внутренним точкам промежутка I, имеют место равенства
по натуральному параметру в точках, соответствующих внутренним точкам промежутка I, имеют место равенства
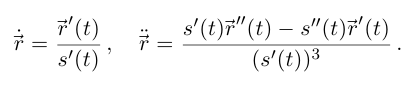
Пусть 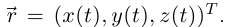 Тогда
Тогда 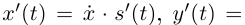
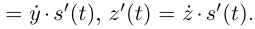 Значит,
Значит, 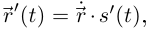 откуда следует первое из утверждений леммы. Далее,
откуда следует первое из утверждений леммы. Далее,
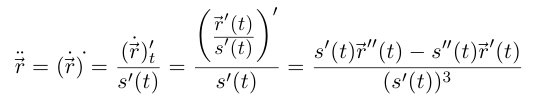
(формула производной дроби применяется покоординатно). Отметим, что 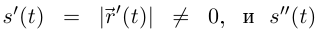 существует по лемме 6.2.
существует по лемме 6.2.
Лемма 6.10. Если 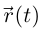 — непрерывно дифференцируемая вектор-функция на интервале I и числовая функция
— непрерывно дифференцируемая вектор-функция на интервале I и числовая функция 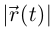 постоянна при
постоянна при 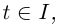 то
то 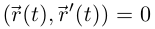 при всех
при всех 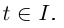
Доказательство очевидно из равенства 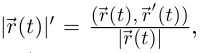 выполненного по лемме 6.2 везде, где
выполненного по лемме 6.2 везде, где 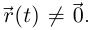 Если
Если 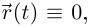 то утверждение и так очевидно.
то утверждение и так очевидно.
Теорема 6.3. Кривизна 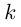 дважды дифференцируемой гладкой кривой Г:
дважды дифференцируемой гладкой кривой Г: 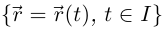 во всех внутренних точках промежутка I вычисляется по формуле
во всех внутренних точках промежутка I вычисляется по формуле
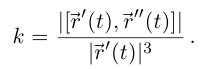
Из леммы 6.9 следует, что 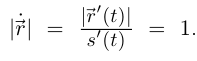 Тогда по лемме 6.10
Тогда по лемме 6.10 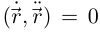 в точках, соответствующих внутренним точкам промежутка I, и, следовательно,
в точках, соответствующих внутренним точкам промежутка I, и, следовательно, 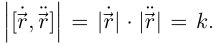 Применяя снова лемму 6.9, получим
Применяя снова лемму 6.9, получим
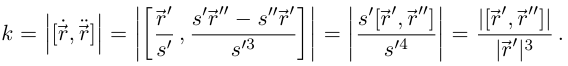
Пример №8
Вычислим кривизну винтовой линии (см. пример 6.6). Имеем
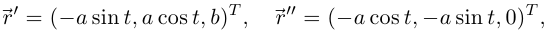
откуда ( — ортонормированный правый базис):
— ортонормированный правый базис):
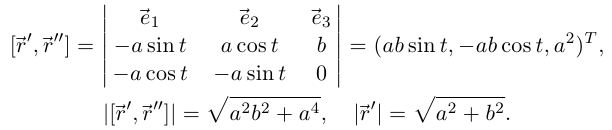
Тогда 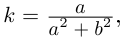 т.е. винтовая линия имеет постоянную кривизну. Кстати, окружность радиуса а можно рассматривать как винтовую линию при
т.е. винтовая линия имеет постоянную кривизну. Кстати, окружность радиуса а можно рассматривать как винтовую линию при 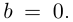 Поэтому кривизна окружности
Поэтому кривизна окружности 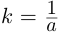 — величина, обратная радиусу.
— величина, обратная радиусу.
Пример №9
Вычислим кривизну плоской дважды дифференцируемой гладкой кривой 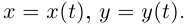
Так как 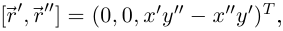 то
то 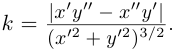
Пример №10
Вычислим кривизну графика дважды дифференцируемой функции 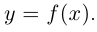
График можно параметризовать так: 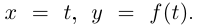 Тогда, подставляя в формулу примера 6.9
Тогда, подставляя в формулу примера 6.9 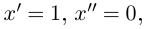 имеем
имеем
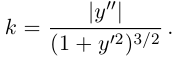
Например, для графика 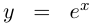 кривизна равна
кривизна равна 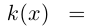
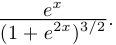 Откуда видно, кстати, что
Откуда видно, кстати, что 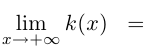
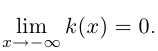
Выясним геометрический смысл кривизны кривой. Единичный направляющий вектор касательной, направленный в сторону возрастания параметра, равен (теорема 6.1 и лемма 6.9)
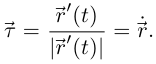
Если данная точка кривой соответствует значению параметра 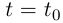 и значению натурального параметра
и значению натурального параметра 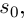 то
то
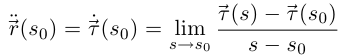
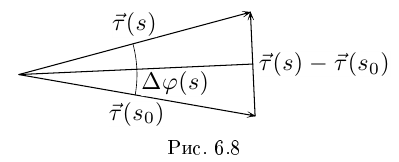
— мгновенная скорость изменения единичного касательного вектора, а кривизна 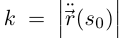 — модуль этой мгновенной скорости. Пусть
— модуль этой мгновенной скорости. Пусть 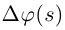 — угол поворота единичного касательного вектора при изменении дуги от
— угол поворота единичного касательного вектора при изменении дуги от 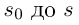 (см. рис. 6.8).
(см. рис. 6.8).
Так как  — дифференцируемая вектор-функция, то
— дифференцируемая вектор-функция, то
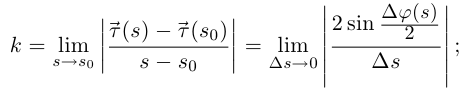
числитель дроби — бесконечно малая величина при 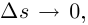 поэтому
поэтому 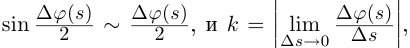 т.е. кривизна кривой в данной точке — это модуль мгновенной скорости вращения единичного касательного вектора.
т.е. кривизна кривой в данной точке — это модуль мгновенной скорости вращения единичного касательного вектора.
Определение 6.16. Радиусом кривизны дважды дифференцируемой гладкой кривой называется величина, обратная значению её кривизны в соответствующей точке (если 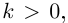 то радиус кривизны
то радиус кривизны 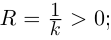 если
если 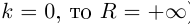 ).
).
Из примера 6.8 и замечания к нему следует, что радиус кривизны окружности в любой точке равен её радиусу.
Кривые с положительной кривизной. Сопровождающий трёхгранник кривой
Как уже отмечалось в §4, единичный вектор касательной к кривой, направленный в сторону возрастания параметра, обозначают 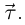 Тогда кривизна кривой в точке, соответствующей значению натурального параметра
Тогда кривизна кривой в точке, соответствующей значению натурального параметра 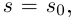 равна
равна 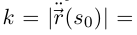
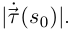
Будем теперь рассматривать дважды дифференцируемые гладкие кривые с положительной кривизной, т.е. такие, для которых 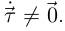 Пусть
Пусть 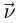 — единичный вектор, сонаправленный с
— единичный вектор, сонаправленный с 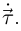 . Тогда из определения кривизны следует, что
. Тогда из определения кривизны следует, что

Это равенство называется первой формулой Френе.
Определение 6.17. Пусть Г: 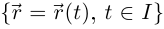 —дважды дифференцируемая гладкая кривая, имеющая в некоторой точке, соответствующей внутренней точке промежутка I, положительную кривизну (т.е.
—дважды дифференцируемая гладкая кривая, имеющая в некоторой точке, соответствующей внутренней точке промежутка I, положительную кривизну (т.е. 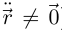 ). Тогда прямая, проходящая через эту точку с направляющим вектором
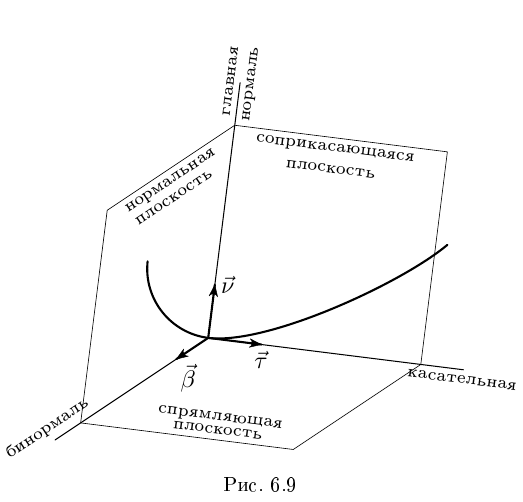
). Тогда прямая, проходящая через эту точку с направляющим вектором 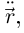 называется главной нормалью к кривой в данной точке, а прямая, проходящая через точку перпендикулярно касательной и главной нормали, называется бинормалью. Плоскость, проходящая через касательную и главную нормаль, называется соприкасающейся плоскостью. Плоскость, проходящая через касательную и бинормаль, называется спрямляющей плоскостью. Плоскость, проходящая через главную нормаль и бинормаль, называется нормальной плоскостью. Такая конструкция называется сопровождающим трехгранником (трехгранником Френе) данной кривой в данной точке (см. рис. 6.9).
называется главной нормалью к кривой в данной точке, а прямая, проходящая через точку перпендикулярно касательной и главной нормали, называется бинормалью. Плоскость, проходящая через касательную и главную нормаль, называется соприкасающейся плоскостью. Плоскость, проходящая через касательную и бинормаль, называется спрямляющей плоскостью. Плоскость, проходящая через главную нормаль и бинормаль, называется нормальной плоскостью. Такая конструкция называется сопровождающим трехгранником (трехгранником Френе) данной кривой в данной точке (см. рис. 6.9).
Замечание:
Так как 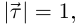 то из леммы 6.10 следует, что
то из леммы 6.10 следует, что  т.е. векторы
т.е. векторы  ортогональны (это уже отмечено в доказательстве теоремы 6.3). Поэтому касательная, главная нормаль и бинормаль — это три взаимно перпендикулярные прямые, а нормальная плоскость —плоскость, проходящая через точку перпендикулярно касательной в данной точке (так можно определить нормальную плоскость для произвольной гладкой кривой). Вектор
ортогональны (это уже отмечено в доказательстве теоремы 6.3). Поэтому касательная, главная нормаль и бинормаль — это три взаимно перпендикулярные прямые, а нормальная плоскость —плоскость, проходящая через точку перпендикулярно касательной в данной точке (так можно определить нормальную плоскость для произвольной гладкой кривой). Вектор  является единичным направляющим вектором бинормали.
является единичным направляющим вектором бинормали.
Напишем уравнения прямых и плоскостей сопровождающего трехгранника в параметризации кривой при помощи параметра t.
Как мы уже отмечали, векторное уравнение касательной в точке, соответствующей значению параметра 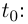
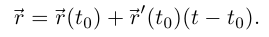
Векторное уравнение нормальной плоскости:
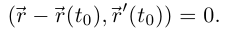
Далее, так как 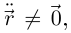 то векторы
то векторы 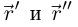 не коллинеарны (по лемме 6.9
не коллинеарны (по лемме 6.9 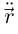 — линейная комбинация
— линейная комбинация 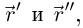 и если
и если 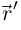 и
и 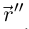 коллинеарны, то они коллинеарны
коллинеарны, то они коллинеарны 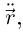 поэтому векторы
поэтому векторы 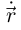 и
и 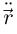 — ненулевые коллинеарные векторы, что противоречит ортогональности). Но если
— ненулевые коллинеарные векторы, что противоречит ортогональности). Но если 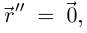 то из леммы 6.9 опять-таки следует коллинеарность векторов
то из леммы 6.9 опять-таки следует коллинеарность векторов 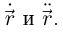 Значит,
Значит, 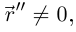 и векторы
и векторы 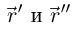 образуют базис в соприкасающейся плоскости. Векторное уравнение соприкасающейся плоскости:
образуют базис в соприкасающейся плоскости. Векторное уравнение соприкасающейся плоскости:
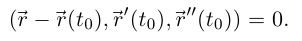
Единичный вектор бинормали 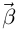 коллинеарен
коллинеарен 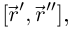 а единичный вектор главной нормали
а единичный вектор главной нормали 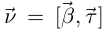 коллинеарен вектору
коллинеарен вектору 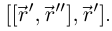 Векторное уравнение главной нормали:
Векторное уравнение главной нормали:
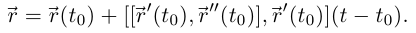
Векторное уравнение бинормали:
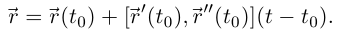
Векторное уравнение спрямляющей плоскости:
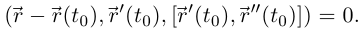
Для трижды непрерывно дифференцируемых гладких кривых первая формула Френе (6.5) может быть дополнена ещё двумя:
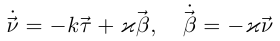
(вторая и третья формулы Френе). Коэффициент 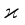 называется кручением кривой и вычисляется по формуле
называется кручением кривой и вычисляется по формуле
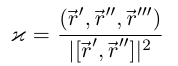
(доказательство этих утверждений мы проводить не будем). Плоские кривые имеют нулевое кручение. Винтовая линия имеет постоянную кривизну (пример 6.8), её кручение также постоянно и в каждой точке равно 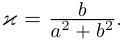
Центр кривизны и эволюта
Определение 6.18. Пусть кривая Г: 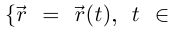
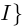 имеет в точке
имеет в точке 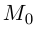 с радиусом-вектором
с радиусом-вектором 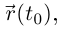 где
где 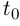 — внутренняя точка промежутка I, положительную кривизну. Тогда центром кривизны кривой в точке
— внутренняя точка промежутка I, положительную кривизну. Тогда центром кривизны кривой в точке 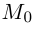 называется точка, радиус-вектор которой равен
называется точка, радиус-вектор которой равен 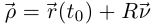 (т.е. точка, лежащая на главной нормали в направлении вектора
(т.е. точка, лежащая на главной нормали в направлении вектора 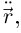 удалённая от точки
удалённая от точки 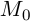 на расстояние, равное радиусу кривизны).
на расстояние, равное радиусу кривизны).
Определение 6.19. Окружность, лежащая в соприкасающейся плоскости кривой, центр которой совпадает с центром кривизны, а радиус — с радиусом кривизны кривой в данной точке, называется окружностью, соприкасающейся с кривой в данной точке.
Приведём без доказательства и без аккуратных формулировок следующие интересные утверждения, которые показывают что соприкасающаяся окружность «теснее других» прилегает к кривой.
1) Из всех прямых и окружностей, проходящих через данную точку кривой, соприкасающаяся окружность «теснее других» прилегает к кривой (при 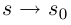 расстояние между точкой кривой и соответствующей точкой окружности, т.е. точкой, длина дуги окружности от которой до данной общей точки кривой и окружности также равно s, есть
расстояние между точкой кривой и соответствующей точкой окружности, т.е. точкой, длина дуги окружности от которой до данной общей точки кривой и окружности также равно s, есть 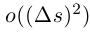 ). Если
). Если 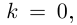 то такой порядок близости даёт касательная прямая, т.е. касательная — это вырожденный случай соприкасающейся окружности, если
то такой порядок близости даёт касательная прямая, т.е. касательная — это вырожденный случай соприкасающейся окружности, если 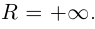 В общем случае такое расстояние для касательной есть
В общем случае такое расстояние для касательной есть 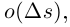 и касательная прилегает к кривой «теснее» всех прямых, проходящих через данную точку кривой.
и касательная прилегает к кривой «теснее» всех прямых, проходящих через данную точку кривой.
2) Если через три точки кривой, соответствующих значениям параметра 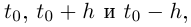 провести окружность, то в пределе при
провести окружность, то в пределе при 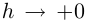 радиус окружности будет стремиться к радиусу кривизны в точке с радиусом-вектором
радиус окружности будет стремиться к радиусу кривизны в точке с радиусом-вектором 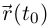 , а координаты центра окружности — к соответствующим координатам центра кривизны. Образно говоря, предельным положением такой окружности будет соприкасающаяся окружность. Если
, а координаты центра окружности — к соответствующим координатам центра кривизны. Образно говоря, предельным положением такой окружности будет соприкасающаяся окружность. Если 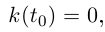 то радиус окружности будет стремиться к
то радиус окружности будет стремиться к 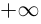 , предельным положением окружности будет касательная прямая.
, предельным положением окружности будет касательная прямая.
Определение 6.20. Если дважды дифференцируемая гладкая кривая в каждой точке имеет положительную кривизну, то множество центров кривизны, соответствующих всем точкам кривой, называется эволютой данной кривой. Кривая по отношению к своей эволюте называется эвольвентой.
Пример №11
Найти эволюту винтовой линии 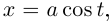
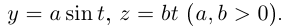
Натуральные уравнения винтовой линии (см. пример 6.6):
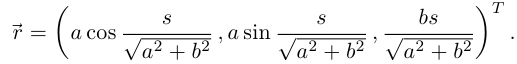
Тогда 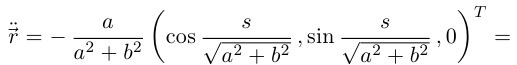
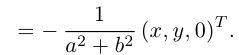
Далее, 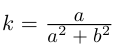 (пример 6.8), поэтому
(пример 6.8), поэтому 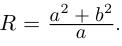 Тогда
Тогда 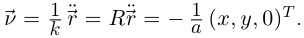 Радиус-вектор центра кривизны
Радиус-вектор центра кривизны
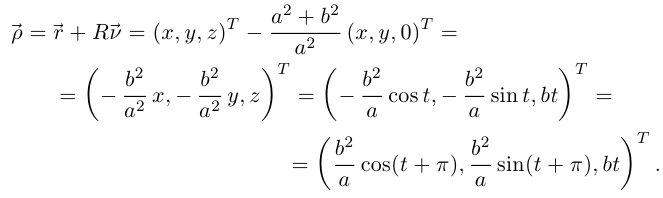
Множество центров кривизны — тоже винтовая линия, у которой та же ось 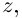 тот же шаг винта
тот же шаг винта 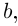 но другой радиус окружности — проекции на плоскость
но другой радиус окружности — проекции на плоскость 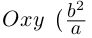 вместо а). Кроме того, винтовая линия и её эволюта «смещены по фазе» на угол
вместо а). Кроме того, винтовая линия и её эволюта «смещены по фазе» на угол 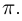
Пример №12
Найти эволюту плоской дважды дифференцируемой гладкой кривой, заданной уравнениями 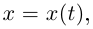
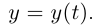
Для плоской кривой 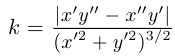 (пример 6.9).
(пример 6.9).
Тогда 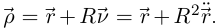 По лемме 6.9 (штрихом обозначаем производную по t; учитываем также, что
По лемме 6.9 (штрихом обозначаем производную по t; учитываем также, что 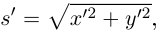
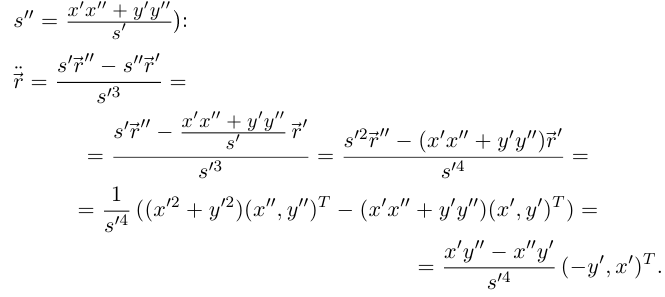
Тогда
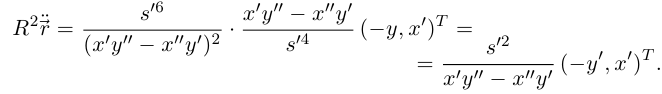
Параметрические уравнения эволюты (текущие координаты точки эволюты, соответствующие значению параметра  обозначим
обозначим 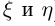 ):
):
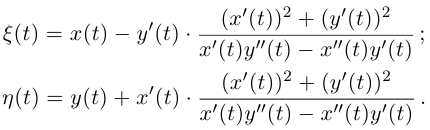
Если плоская кривая является графиком дважды дифференцируемой функции 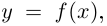 то её можно параметризовать так:
то её можно параметризовать так: 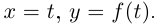 Тогда
Тогда 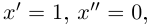 и
и
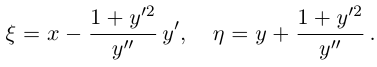
Пример №13
Найти эволюту эллипса 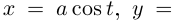
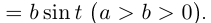
Имеем по формулам примера 6.12
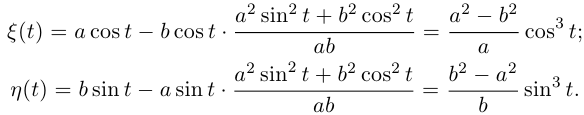
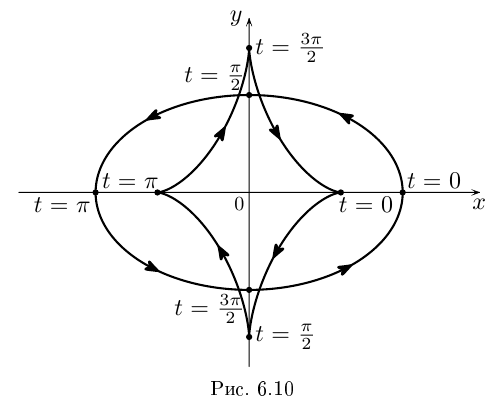
Это — астроида (см. рис. 6.10).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |