Декартовы координаты в пространстве - определение и примеры с решением

Содержание:

Как известно, расположение точки на координатной прямой однозначно описывается одной координатой. Из курса планиметрии вы знакомы с прямоугольной декартовой системой координат на плоскости. Напомним, что для ее введения через произвольную точку плоскости О проводят две взаимно перпендикулярные координатные оси Ох и Оу (рис. 1). При таких условиях каждой точке плоскости А ставится в соответствие упорядоченная пара чисел (х;у) — координаты оснований перпендикуляров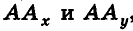

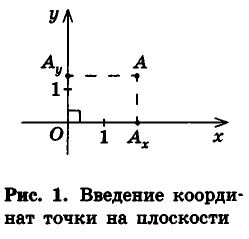
Вполне естественно, что для описания расположения точки в пространстве необходимо иметь три координаты — ведь, например, бабочка перемещается в воздухе не только вперед-назад и вправо-влево, но и вверх-вниз.

Итак, рассмотрим три взаимно перпендикулярные координатные оси 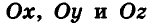с общей точкой О (началом координат) и равными единичными отрезками на осях (рис. 2). Ось Ох называют осью абсцисс, ось Оу — осью ординат, ось 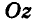— осью аппликат, а плоскости 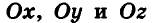— координатными плоскостями. Заданную таким образом систему координат называют прямоугольной декартовой системой координат в пространстве.

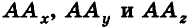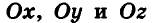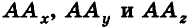Для определения координат произвольной точки пространства А проведем из данной точки перпендикуляры к осям соответственно (рис. 3). Тогда координаты х, у, точек на осях 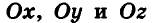соответственно являются координатами точки А в данной системе координат. Коротко это записывают так: 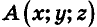, где х — абсцисса, у — ордината, 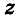— аппликата точки А.

Координаты точки А можно определить и по-иному. Например, для получения координаты Ах проведем перпендикуляр АА₀ к плоскости Оху, а потом из точки А₀ проведем перпендикуляр 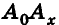к оси Ох (рис. 3). Тогда по теореме о трех перпендикулярах 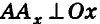, то есть полученная таким образом координата Ах совпадает с определенной ранее и является абсциссой точки А (аналогичные рассуждения для ординаты и аппликаты проведите самостоятельно).

Значения координат точки А можно также получить, если провести через эту точку три плоскости, параллельные координатным плоскостям 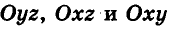(рис. 3). В этом случае точки 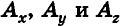являются точками пересечения проведенных плоскостей с координатными осями (объясните почему).

Итак, в прямоугольной декартовой системе координат каждой точке пространства ставится в соответствие единственная упорядоченная тройка чисел (x;y;z), и наоборот: каждой тройке чисел (x;y;z) соответствует единственная точка пространства.

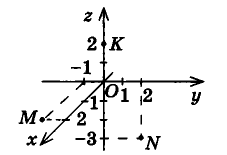
Очевидно, что если точка принадлежит одной из координатных плоскостей, то некоторая ее координата равна нулю. Так, на рисунке 4 точка М принадлежит плоскости Оху и имеет координаты (2;-1;0), а точка N плоскости Оуг — координаты (0; 2; — 3). Соответственно точки, принадлежащие координатным осям, имеют две нулевые координаты: например, координаты точки К оси Ог равны (0; 0; 2). Очевидно также, что все три координаты начала координат нулевые: 0(0;0;0). Условия, при которых та или иная координата точки равна нулю, исследуйте самостоятельно.

Пример:

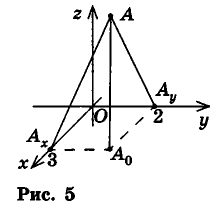
Найдите координаты проекций точки А(3;2;4) на координатные плоскости.

Решение:

Проведем из данной точки перпендикуляр АА₀ к плоскости Оху и перпендикуляры АА_Х и АА_у к осям Ох и Оу соответственно (рис. 5). Найдем координаты точки А₀.

Так как — проекции наклонных и 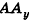у на плоскость Оху, то по теореме о трех перпендикулярах 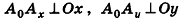. Так как по определению координат точки в пространстве координата точки Ах на оси Ох и координата точки Ау на оси Оу равны соответствующим координатам точки А, то Ах (3; 0; 0), Ау (0; 2; 0). Отсюда А₀ (3; 2; 0).

Рассуждая аналогично, определяем, что проекции точки А на плоскости Oxz и Оуz имеют координаты (3;0;4) и (0; 2; 4) соответственно.

Ответ: (3;2;0), (3;0;4), (0;2;4).

Основные задачи координат

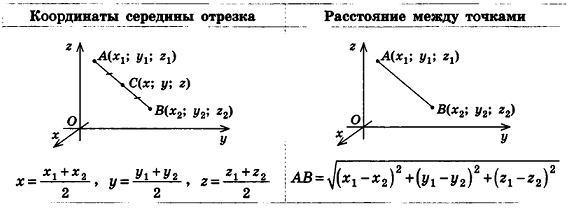
Опираясь на соответствующие свойства координат на плоскости, докажем формулы координат середины отрезка и расстояния между точками в пространстве.

Напомним, что в планиметрии каждая координата середины отрезка равна полусумме соответствующих координат его концов. Такое же свойство сохраняется и в стереометрии. Теорема (формулы координат середины отрезка в пространстве) Координаты середины отрезка вычисляются по формулам:

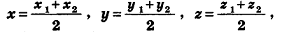
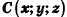где - концы отрезка, — середина отрезка.

Доказательство:

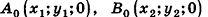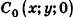Опустим из точек А, В и С перпендикуляры на плоскость Оху. Основания этих перпендикуляров — точки и соответственно. Рассмотрим случай, когда точки 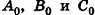не совпадают (рис. 6). Так как проведенные к одной плоскости перпендикуляры параллельны и лежат в одной плоскости, а точка С — середина отрезка АВ, то по теореме Фалеса точка С0 является серединой отрезка A₀B₀. По формулам координат середины

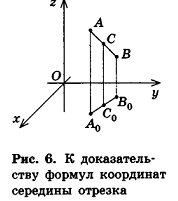
отрезка на плоскости имеем: 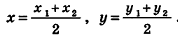. В случае, когда точки 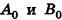, а значит, и С₀ совпадают, эти формулы также справедливы (проверьте это самостоятельно).

Аналогично, проведя из данных точек перпендикуляры к плоскости 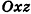, получаем 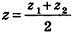. Теорема доказана.

Как известно из курса планиметрии, расстояние между точками 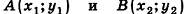вычисляется по формуле 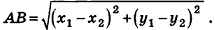Выведем пространственный аналог этой формулы.

Теорема (формула расстояния между точками в пространстве) Расстояние между точками 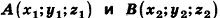вычисляется по формуле

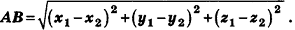
Доказательство:

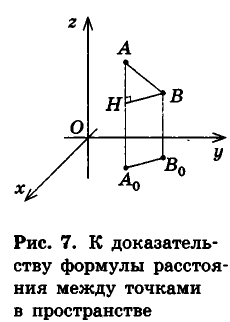
Рассмотрим сначала случай, когда отрезок АВ не параллелен плоскости Оху (рис. 7).

Опустим из точек А и В перпендикуляры 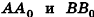на плоскость Оху, 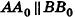. Ясно, что точки 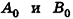имеют координаты 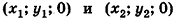соответственно. По формуле расстояния между точками на плоскости 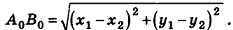Плоскость, проходящая через точку В параллельно Оху, пересекает прямую АА₀ в некоторой точке Н, причем ВН = А₀В₀ как противолежащие стороны образованного параллелограмма. Более того, 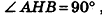, поскольку проведенная плоскость параллельна Оху, а прямая АА₀ перпендикулярна этим плоскостям. Так как 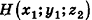то AH = 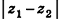. Следовательно, из треугольника АНВ по теореме Пифагора

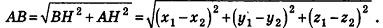
В случае, когда отрезок АВ параллелен оси 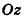или принадлежит ей, его длина равна 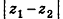. Такой же результат дает и только что полученная формула при 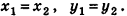Случай,

когда отрезок АВ параллелен плоскости Оху, рассмотрите самостоятельно.

Пример:

Докажите, что четырехугольник ABCD с вершинами В(4;—3; 2), C(6;3;-4), D (0; 7; -6) является параллелограммом.

Решение:

Найдем координаты середин отрезков АС и BD.

Для отрезка АС: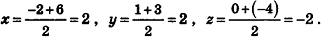

Для отрезка BD: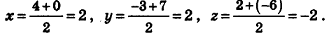

Следовательно, отрезки АС и ВD имеют общую середину. Это значит, что прямые АС и BD пересекаются, то есть точки А, В, С и D лежат в одной плоскости. Диагонали четырехугольника ABCD точкой пересечения делятся пополам, таким образом, ABCD — параллелограмм по признаку.

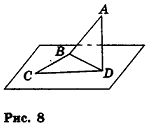
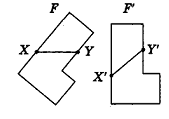
Отметим, что при решении аналогичной задачи в курсе планиметрии мы использовали и другой способ — доказывали попарное равенство противолежащих сторон данного четырехугольника. Но в пространстве этот способ неприемлем, так как из равенств AB = CD и AD = BC не следует, что точки А, В, С и D лежат в одной плоскости. Действительно, четырехугольник ABCD может оказаться пространственным (на рисунке 8 такой четырехугольник получен перегибом параллелограмма ABCD по прямой BD). Очевидно, что в этом случае пространственный четырехугольник ABCD удовлетворяет условиям АВ = CD и AD-ВС, но не является параллелограммом.

Второй способ решения этой задачи будет рассмотрен в § 2.

Пример:

На оси аппликат найдите точку С, равноудаленную от точек А(1;0;3) и В(4;3;-1).

Решение:

Так как искомая точка лежит на оси аппликат, то C(0;0;z). Найдем z, воспользовавшись условием АС = ВС. Имеем: 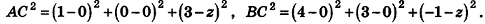Приравняв эти выражения, получим 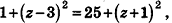откуда 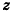= -2. Следовательно, искомая точка С(0;0;-2).

Ответ: (0; 0; - 2).

Движения в пространстве

Напомним, что движением на плоскости мы называли геометрическое преобразование, сохраняющее расстояния между точками. Так же определяют движение и в пространстве, причем все свойства движений, известные из курса планиметрии, в стереометрии сохраняются: при движении прямые переходят в прямые, лучи — в лучи, отрезки — в отрезки, и углы между лучами не изменяются.

Свойства движений в пространстве

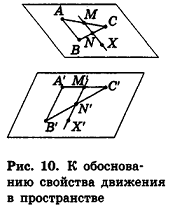
Новым свойством движения в пространстве является то, что движение переводит плоскость в плоскость.

Действительно, пусть точки А, В и С, не лежащие на одной прямой, при движении переходят в точки А', В' и С', также не лежащие на одной прямой (рис. 10). Покажем, что при этом движении плоскость ABC переходит в плоскость А'В'С'. Через произвольную точку X плоскости ABC проведем прямую, пересекающую две стороны треугольника ABC в точках М и N. Очевидно, что при движении эти точки перейдут в точки М' и N', лежащие на соответствующих сторонах треугольника А'В'С'. Таким образом, прямая M'N', в которую переходит прямая MN, принадлежит плоскости А'В'С', то есть точка Х' в которую переходит точка X, принадлежит прямой M'N', а следовательно, и плоскости А'В'С'. Это значит, что произвольная точка плоскости ABC при движении переходит в точку плоскости А'В'С'.

Аналогично можно доказать, что каждую точку плоскости А'В'С' можно получить из точки плоскости ABC при рассматриваемом движении. Итак, при движении плоскость ABC переходит в плоскость А'В'С'.

Так же как и на плоскости, в пространстве две фигуры называются равными, если они совмещаются движением.

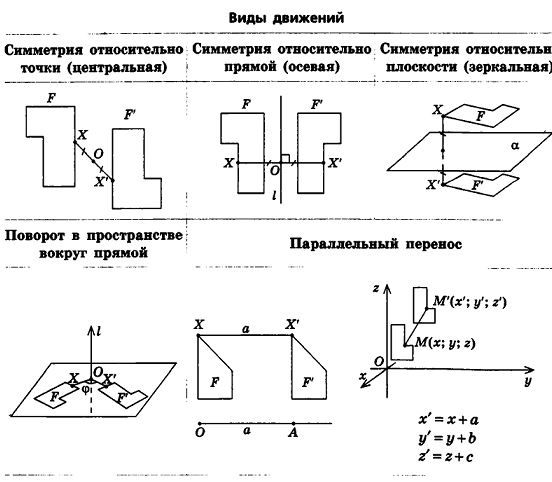
Симметрия в пространстве

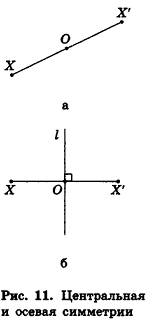
Симметрия как один из видов геометрических преобразований знакома вам из курса планиметрии. Преобразования симметрии относительно точки (центральная симметрия) и относительно прямой (осевая симметрия) в пространстве определяют так же, как и на плоскости:

• точки X и X' называются симметричными относительно точки О, если точка О — середина отрезка XX' (рис. 11, а); точка О называется центром симметрии;
• точки X иХ' называются симметричными относительно прямой I, если эта прямая перпендикулярна отрезку XX' и проходит через его середину (рис. 11, б); прямая I называется осью симметрии.

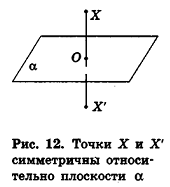
Рассмотрим еще один вид симметрии в пространстве. Пусть а — фиксированная плоскость, X — произвольная точка вне ее. Проведем перпендикуляр ХО к плоскости а и на луче ХО отложим отрезок ОХ', равный ХО, но лежащий в другом полупространстве относительно плоскости а (рис. 12). Мы получили точку X', симметричную точке X относительно плоскости а.

Определение:

Точки X и X' называются симметричными относительно плоскости а, если эта плоскость перпендикулярна отрезку XX' и проходит через его середину. Точки плоскости а считаются симметричными сами себе.

При этом плоскость а называется плоскостью симметрии.

Очевидно, что точкой, симметричной точке X' относительно плоскости а, является точка X.

Определение:

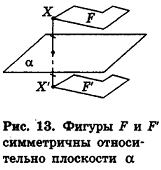
Преобразованием симметрии (симметрией) относительно плоскости а называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X' фигуры F', симметричную X относительно плоскости а.

При этом фигуры F и F' называются симметричными относительно плоскости а (рис. 13).

Наглядно представить симметрию относительно плоскости можно с помощью плоского зеркала. Любой объект и его изображение симметричны относительно плоскости зеркала (рис. 14). Поэтому симметрию относительно плоскости иначе называют зеркальной симметрией.

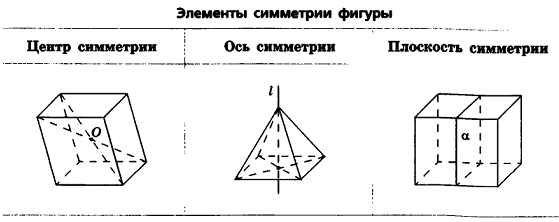
Если преобразование симметрии относительно плоскости а переводит фигуру F в себя, то такая фигура называется симметричной относительно плоскости а, а сама плоскость а — плоскостью симметрии фигуры F. Например, плоскостью симметрии прямой является любая перпендикулярная ей плоскость (рис. 15).

Центры, оси и плоскости симметрии фигуры, если они у нее есть, называются элементами симметрии этой фигуры.

Несложно доказать, что точки, симметричные точке A(x;y;z) относительно координатных плоскостей, осей и начала координат, имеют следующие координаты:

Теорема (основное свойство зеркальной симметрии) Зеркальная симметрия является движением.

Доказательство:

Пусть точки А и В при симметрии относительно плоскости а переходят в точки А' и В' соответственно. Введем систему координат так, чтобы плоскость Оху совпала с а (рис. 16).

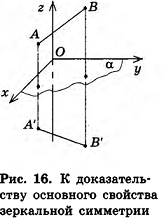
Так как точки, симметричные относительно плоскости Оху, имеют одинаковые абсциссы и ординаты, но противоположные аппликаты, то для точек 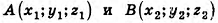получим 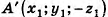, 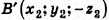. Тогда по формуле расстояния между точками находим:

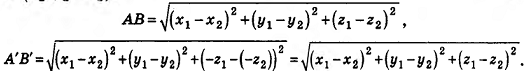
Таким образом, АВ = А'В'. Значит, зеркальная симметрия сохраняет расстояния между точками, то есть является движением.

Теорема доказана.

Из доказанной теоремы следует, что зеркальная симметрия обладает всеми свойствами движения.

Пример №1

Докажите, что если две прямые зеркально симметричны, то они лежат в одной плоскости.

Решение:

Рассмотрим произвольные точки А к В прямой а, которые при зеркальной симметрии относительно плоскости а переходят в точки А' и В' прямой а'. По определению симметрии относительно плоскости 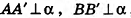, следовательно, 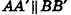. Очевидно, что точки А, А', В и В' лежат в плоскости этих параллельных прямых, то есть прямые а и а' также лежат в этой плоскости.

Самые разнообразные виды пространственной симметрии мы наблюдаем в живой и неживой природе, искусстве, технике и т. д. В основе строения живых форм лежит принцип симметрии, причем природа гармонично объединяет различные виды симметрий с почти математической строгостью (рис. 17).

Совершенную симметричную форму имеют природные многогранники — кристаллы (подробнее рассмотрим их в § 12). Физики утверждают, что симметрия является фундаментальным свойством природы, с которым связаны законы сохранения энергии и импульса, строение атомов и молекул, а также особенности природных явлений.

Невозможно переоценить значение симметрии в искусстве. В древнегреческой архитектуре симметрия была воплощением законов целесообразности и гармонии (рис. 18). Идеи зеркальной симметрии широко отражены в живописи Средневековья.

В литературных произведениях существует симметрия образов, ситуаций, мышления. Вспомним хотя бы «закон мести» в греческой трагедии: виновник преступления в конце концов сам становится жертвой такого же преступления.

Яркими примерами симметрии образов являются персонажи комедии Н. В. Гоголя «Ревизор» Добчинский и Бобчинский — сам автор отмечает, что они чрезвычайно похожи друг на друга (рис. 19). Симметричными можно считать и литературные образы героев-антиподов, противостояние между которыми составляет основной конфликт литературного произведения: Шерлок Холмс и профессор Мориарти у А. Конана Дойля, доктор Джекил и мистер Хайд у P. JI. Стивенсона и т. д.

В музыке построение отдельных мелодичных форм также подчиняется законам симметрии. Прослушайте «Рондо-каприччио» великого Бетховена — композитор использует основную тему как своеобразную плоскость симметрии, от которой как бы отражаются отдельные эпизоды и вариации. Симметрия в музыке наглядно проявляется даже через нотную запись (рис. 20).

Глава I. Координаты, векторы и геометрические преобразования в пространстве

Неисчерпаемые возможности симметрии и то широкое применение, которое она получила в разных областях человеческой деятельности, подтверждают универсальность геометрических знаний и значимость геометрии в общечеловеческой культуре.

Поворот в пространстве

Напомним, что на плоскости мы выполняли поворот фигуры вокруг данной точки О в заданном направлении на данный угол. Но в пространстве такое описание поворота не является однозначным: действительно, через фиксированную точку О проходит бесконечно много плоскостей, и в каждой из них поворот фигуры вокруг точки О на данный угол приведет к различным результатам.

Между тем, открывая дверь или переворачивая страницу книги, мы поворачиваем все точки фигуры в одном направлении на определенный угол, причем все точки некоторой прямой остаются неподвижными. Попробуем на основании этих наглядных примеров приблизиться к строгому определению поворота в пространстве.

Для этого рассмотрим фиксированную прямую I и произвольную точку X (рис. 21). Проведем через точку X плоскость а, перпендикулярную I, и обозначим точку О пересечения плоскости а с прямой I. В плоскости а выполним поворот точки X вокруг точки О на угол ф, т. е. построим точку X' так, чтобы 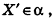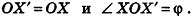Такой переход точки X в точку X' называется поворотом вокруг прямой I на угол ф.

Напомним, что на плоскости мы характеризовали поворот и направлением — по часовой стрелке или против часовой стрелки. В пространстве направление поворота на плоскости а зависит от выбора стороны, с которой мы смотрим на эту плоскость (об этом, в частности, речь будет идти в п. 2.5). Поэтому договоримся считать прямую, вокруг которой выполняется поворот, ориентированной

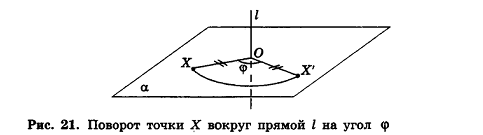
(т. е. осью с заданным направлением) и рассматривать поворот по часовой стрелке или против часовой стрелки, если смотреть на плоскость с положительного направления этой оси. Например, на рисунке 22 показано направление поворота точек плоскости а вокруг оси I против часовой стрелки.

Поворотом фигуры F вокруг ориентированной прямой I на угол ф называется преобразование фигуры F в фигуру F', при котором каждая точка X фигуры F (Х&1) переходит в точку X' фигуры F так, что 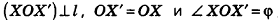, где О - точка пересечения плоскости, проходящей через точку X перпендикулярно прямой I, с прямой I.

Все углы измеряются по часовой стрелке (или все — против часовой стрелки), точки прямой I при повороте переходят сами в себя.

Иначе говоря, при повороте вокруг ориентированной прямой I каждая точка фигуры F смещается в заданном направлении на данный угол по дуге окружности, плоскость которой перпендикулярна прямой I, центр принадлежит этой прямой, а радиус равен расстоянию от данной точки фигуры F до прямой I. На рисунке 23 фигура F переходит в фигуру F' при повороте вокруг оси I на угол ф против часовой стрелки.

Прямую I называют осью поворота (или осью вращения), а угол ф — углом поворота.

Теорема

(основное свойство поворота в пространстве) Поворот вокруг прямой является движением.

Доказательство:

Пусть при повороте вокруг оси I на угол ф (0° < ф < 180°) точки А и В переходят в точки А' и В' соответственно. Докажем, что АВ =А'В'.

Рассмотрим общий случай, когда прямые АВ и I скрещиваются и не являются перпендикулярными. Проведем через точки А и В

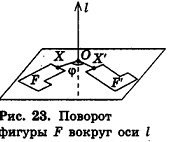
плоскости аир, перпендикулярные прямой I и пересекающие ее в точках Oj и 02 соответственно (рис. 24).

Опустим из точки А перпендикуляр АС на плоскость 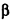. Рассмотрим в плоскости а поворот вокруг точки О₁, а в плоскости 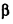— поворот вокруг точки О₂ на угол ф. При таких поворотах точки А к В переходят в точки А' и В' Опустим из точки А' перпендикуляр А'С' на плоскость .

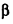Очевидно, что плоскости а и 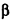, перпендикулярные прямой I, параллельны. Отрезки 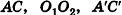перпендикулярны этим плоскостям, параллельны и равны. Следовательно, четырехугольники 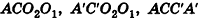являются прямоугольниками, откуда следует равенство треугольников 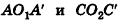по трем сторонам. Это значит, что углы 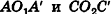являются равными и равны углу ф. Поэтому при повороте в плоскости Р на угол ф вокруг точки 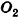точка С переходит в С'. По свойству поворота на плоскости получаем, что .

Прямоугольные треугольники ABC и А'В'С' равны по двум катетам , откуда АВ = А'В', что и требовалось доказать.

Другие случаи взаимного расположения прямых АВ а I, а также доказательство для случая ф>180° рассмотрите самостоятельно.

Если при повороте вокруг некоторой прямой I фигура F переходит в себя, то говорят, что эта фигура имеет поворотную симметрию (или симметрию вращения). Примеры пространственных фигур, обладающих поворотной симметрией, будут рассмотрены дальше.

Заметим также, что поворот вокруг прямой I на 180° является осевой симметрией относительно прямой I (докажите это самостоятельно).

Параллельный перенос в пространстве

Параллельный перенос в пространстве является разновидностью параллельного проектирования для случая, когда плоскость проектируемой фигуры параллельна плоскости проекции (или совпадает с ней).

Напомним, что сонаправленными лучами мы называли:

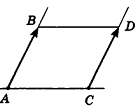
1. два луча одной прямой, один из которых является частью другого (например, лучи АС и ВС на рис. 25, а);
2. два параллельных луча, лежащих в плоскости по одну сторону от прямой, проходящей через их начальные точки (например, лучи АВ и CD на рис. 25, б).

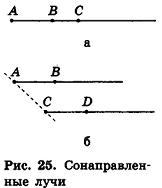
Определение параллельного переноса в стереометрии ничем не отличается от планиметрического. Параллельным переносом, фигуры F в направлении луча OA на расстояние а называется преобразование фигуры F в фигуру F', при котором каждая точка X фигуры F переходит в точку X' фигуры F' так, что лучи XX' и OA сонаправлены и XX' = а (рис. 26).

Теорема (основное свойство параллельного переноса в пространстве)

Параллельный перенос в пространстве является движением.

Доказательство:

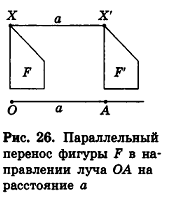
Пусть при параллельном переносе точки А и В переходят в точки А' и В' соответственно. Покажем, что АВ = А'В' Если точки А, В, А' и В' не лежат на одной прямой (рис. 27, а), то отрезки АА' и ВВ' параллельны и равны. Отсюда АА'В'В — параллелограмм, то есть АВ = А'В' как противолежащие стороны параллелограмма. В случае, когда точки А, В, А' и В' лежат на одной прямой (рис. 27, б), получаем: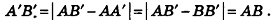

В дальнейшем, изучая векторы в пространстве, мы будем рассматривать параллельный перенос на вектор .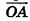

Убедитесь самостоятельно в том, что рассмотренное доказательство справедливо и для других случаев расположения точек А, В, А и В' на одной прямой.

Следствие 1

Параллельный перенос переводит прямую в параллельную прямую (или в себя), отрезок — в равный ему отрезок, угол — в равный ему угол.

Следствие 2

Параллельный перенос переводит плоскость в параллельную плоскость (или в себя).

Действительно, поскольку параллельный перенос является движением, то он переводит произвольную плоскость а в плоскость 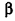. Если эти плоскости не совпадают (рис. 28), то произвольные прямые 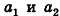плоскости а переходят в параллельные им прямые 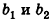соответственно, и по признаку параллельности плоскостей .

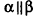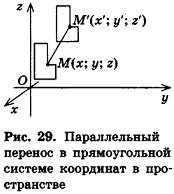
Так же как и на плоскости, в пространстве при условии введения системы координат (рис. 29) параллельный перенос, который переводит точку M(x;y;z) в точку M'(x';y';z'), можно задать формулами:

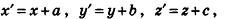
где 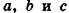— некоторые числа, одни и те же для всех точек пространства (доказательство этого факта в стереометрии аналогично планиметрическому). В качестве примера применения формул параллельного переноса рассмотрим другой способ решения задачи п. 1.2.

Пример №2

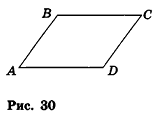
Докажите, что четырехугольник ABCD с вершинами А(-2;1;0), В(4;-3;2), С(б;3;-4), £>(0;7;-б) является параллелограммом.

Решение:

Покажем, что параллельный перенос, который переводит точку В в точку С, переводит точку А в точку D (рис. 30). Сначала найдем формулы этого переноса. Подставив в общие формулы параллельного переноса координаты

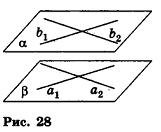
точек В и С, получим уравнения, из которых определим а, b и с: 6 = 4 + а; 3 = -3+b; -4 = 2+ с. Отсюда а = 2; b = 6; с = -6.

Следовательно, искомый перенос задается формулами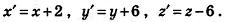

Подставив в эти формулы координаты точек А и D, получим правильные равенства: 0 = -2+2, 7 = 1+6, -6=0-6.

Так как по условию ABCD — четырехугольник, его вершины не лежат на одной прямой. Следовательно, по свойству параллельного переноса в четырехугольнике ABCD две стороны параллельны и равны, то есть ABCD — параллелограмм.

Об ориентации поверхности. Лента Мебиуса

При рассмотрении преобразования поворота было отмечено, что направление поворота в данной плоскости фактически зависит от выбора стороны, с которой мы смотрим на плоскость. Такой выбор стороны называется ориентацией плоскости.

Аналогично можно определить понятие ориентации и для других двусторонних поверхностей в пространстве (поверхности куба, цилиндра, шара и др.). Представим себе, что мы закрасили одну из сторон рассматриваемой поверхности — очевидно, что другая ее сторона останется незакрашенной.

Но эта очевидность только кажущаяся, так как существуют поверхности, которые невозможно ориентировать. Самой простой из них является так называемая лента Мебиуса (рис. 31), открытая в 1858 году немецким астрономом и математиком Августом Мебиусом. Изготовить ее модель очень просто: для этого бумажную ленту, имеющую форму прямоугольника ABCD (рис. 32, а), нужно склеить так, чтобы вершина А совместилась с вершиной С, а вершина В — с вершиной D (рис. 32, б).

Удивительно, но лента Мебиуса является односторонней поверхностью. Чтобы убедиться в этом, попробуйте начать закрашивать ленту с любого места, постепенно перемещаясь по ее поверхности, —

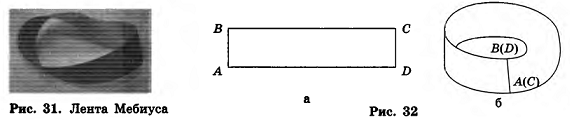
Глава I. Координаты, векторы и геометрические преобразования в пространстве в результате вся поверхность окажется закрашенной. Значит, муравьям, которые ползут по ленте Мебиуса на гравюре М. Эшера (рис. 33), не нужно переползать через край ленты, чтобы попасть на ее «противоположную сторону».

Еще одно интересное свойство ленты Мебиуса заключается в том, что она имеет только один край. Действительно, если выбрать в любом месте края ленты точку и начать от нее двигаться вдоль края, со временем мы вернемся в ту же исходную точку, причем все точки края будут пройдены (проверьте это самостоятельно).

И наконец, предлагаем вам еще один эксперимент: проведите на ленте Мебиуса среднюю линию (т. е. отрезок, который соединяет середины противолежащих сторон АВ и CD прямоугольника, из которого была склеена лента) и попробуйте разрезать по ней ленту. Оказывается, что вместо двух отдельных частей получается дважды перекрученная лента Мебиуса. Невероятно, но это так!

Лента Мебиуса стала первым примером неориентированной поверхности. Позднее были открыты и другие — например, так называемая бутылка Клейна (рис. 34).

Свойство односторонности ленты Мебиуса нашло довольно широкое техническое применение. В XX веке такую ленту использовали для записи звука на непрерывную магнитную пленку, а также как красящую ленту в первых (матричных) принтерах. Ременные передачи или ленты конвейера, имеющие форму ленты Мебиуса, применяют и сегодня, ведь такие ленты служат вдвое дольше, чем обычные, так.как изнашиваются вдвое медленнее (объясните почему). В современной математике существует специальный раздел «топология», в котором рассматриваются, в частности, формы и ориентация поверхностей. А в мировой культуре лента Мебиуса остается символом удивительных открытий, которые до сих пор скрывает геометрия.

Подобие пространственных фигур

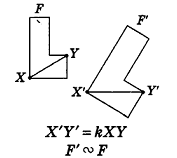
Так же как и на плоскости, преобразование фигуры F в пространстве называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одном и том же отношении. Это значит, что если две произвольные точки X и Y фигуры F при преобразовании подобия переходят в точки X' и У' фигуры F', то X'Y' = kXY , где k — коэффициент подобия (k > 0).

Преобразование подобия в пространстве

Преобразование подобия в пространстве переводит прямые в прямые, лучи — в лучи, отрезки — в отрезки, а также сохраняет углы между лучами (доказательство этих свойств в стереометрии не отличается от планиметрического). Новым свойством подобия в пространстве является то, что преобразование подобия переводит плоскости в плоскости (докажите это утверждение самостоятельно, аналогично соответствующему обоснованию для движения в п. 2.1).

Две фигуры в пространстве называются подобными, если они переводятся одна в другую преобразованием подобия. Напомним некоторые свойства подобия.

1. Любая фигура подобна сама себе: 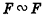(рефлексивность подобия).
2. Если 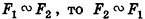(симметричность подобия).
3. Если 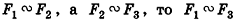(транзитивность подобия).
4. Отношение площадей подобных фигур равно квадрату коэффициента подобия: если 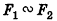с коэффициентом k, то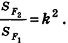

Пример №3

Через точку Р проведены три луча, не принадлежащие одной плоскости и пересекающие параллельные плоскости а и 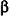в точках А, В, С и 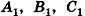соответственно (рис. 37). Докажите подобие треугольников ABC и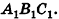

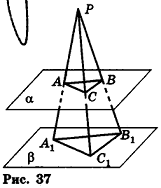
Решение:

Согласно свойству параллельных плоскостей плоскость РАВ пересекает плоскости по параллельным прямым 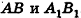. Отсюда треугольники РАВ и 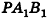подобны по двум углам, следовательно, 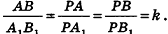Аналогично доказываем подобие треугольников 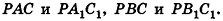Так как эти пары треугольников имеют с треугольниками РАВ и 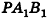общие стороны, то коэффициенты подобия также равны k. Следовательно, 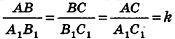, т. е. треугольники ABC и подобны по трем сторонам.

Гомотетия в пространстве

Напомним, что гомотетией с центром в точке О и коэффициентом k>0 называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X' фигуры F', лежащую на луче ОХ, и ОХ' = кОХ.

Гомотетия является преобразованием подобия (доказательство этого факта в стереометрии аналогично планиметрическому). Докажем еще одно свойство гомотетии в пространстве.

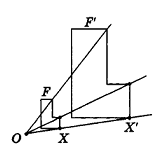
Теорема (свойство гомотетии в пространстве)

Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя.

Доказательство:

Пусть а — данная плоскость, точка О — центр гомотетии. Рассмотрим случай, когда коэффициент гомотетии h не равен единице (рис. 38).

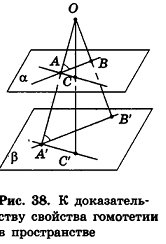
Данная гомотетия переводит любые точки А и В плоскости а в точки А' и В' соответственно, причем 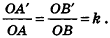Тогда треугольники АОВ и А'ОВ' подобны по двум пропорциональным сторонам и углу между ними. Из подобия этих треугольников следует равенство соответствующих углов ОАВ и ОАВ', а следовательно, параллельность прямых АВ и А'В'.

Аналогично, рассматривая в плоскости а прямую АС, пересекающуюся с АВ, можно доказать, что при гомотетии она переходит в параллельную прямую А'С'. Следовательно, при данной гомотетии плоскость а переходит в плоскость а', содержащую точки А, В' и С'. Так как А'В' || АВ и А'С || АС , а плоскости а и а' не совпадают, то по признаку параллельности плоскостей а'||а.

Очевидно, что в случае k = l плоскость а при гомотетии переходит в себя. Теорема доказана.

Ясно, что плоскость, проходящая через центр гомотетии, при этом преобразовании также переходит в себя.

Обратим внимание и на такой интересный факт (даем его без доказательства): если две фигуры подобны, то одну из них можно получить из другой путем последовательного применения гомотетии и движения.

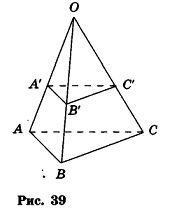
Пример №4

При гомотетии с центром О (2; — 3; 1) треугольник ABC переходит в треугольник А'В'С'. Найдите координаты точек В' и С', если А(б;-1;5), А'(4;-2;3), В(0;1;7), С(-4;-5;-7).

Решение:

Найдем длины отрезков OA и OA':

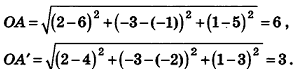
Так как по определению гомотетии OA' = kOA, то k = 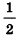. Следовательно, точки А', В' и С' — середины отрезков OA, OB и ОС соответственно (рис. 39).

По формулам координат середины отрезка получаем:

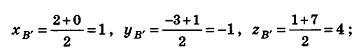
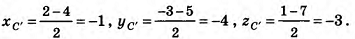
Следовательно, B'(l;-1;4), С'(-1;-4-3).

Ответ: В'(1;-1;4), С'(-1;-4-3).

Подобие пространственных фигур находит широкое применение на практике. Например, архитекторы и строители, проектируя размещение новых зданий и сооружений на местности, предлагают заказчикам макеты строящихся объектов (рис. 40).

Логическое отношение эквивалентности

Как мы уже отмечали, отношение подобия на множестве геометрических фигур является рефлексивным, симметричным и транзитивным. Эти три свойства присущи и некоторым другим отношениям, причем не только геометрическим.

Например, для любых двух натуральных чисел а и b можно рассматривать отношение «число а дает при делении на 5 тот же остаток, что и число Ь» (обоснуйте самостоятельно рефлексивность, симметричность и транзитивность такого отношения). На множестве людей указанные свойства имеет отношение «а является гражданином той же страны, что и b» (если не принимать во внимание людей без гражданства и людей с двойным гражданством), а на множестве слов русского языка — отношение «слово а имеет тот же корень, что и слово b.

В логике отношения, имеющие свойства рефлексивности, симметричности и транзитивности, называют отношениями эквивалентности. Наличие такого отношения на множестве однородных предметов позволяет разделить их на классы эквивалентности — подмножества, элементы которых имеют общие свойства. Например, отношение подобия на множестве многоугольников позволяет нам рассматривать как отдельные классы равносторонние треугольники, квадраты и т. д. Действительно, все фигуры одного класса имеют общие геометрические свойства, которые сохраняются при преобразовании подобия. О таких фигурах. говорят, что они являются равными с точностью до подобия (другими словами, имеют одинаковую форму, но отличаются размерами). Для изучения геометрических свойств фигур определенного класса достаточно рассмотреть одну произвольную фигуру и на ее примере исследовать особенности остальных фигур данного класса.

Деление на классы эквивалентности используют не только математики. Так, филологи, рассматривая для существительных русского языка отношение «слова а и b имеют одинаковые окончания при склонении», делят все существительные на три склонения. Идея деления на классы эквивалентности лежит в основе многих химических и биологических классификаций. Вспомните, как использовал эту идею в периодической таблице химических элементов Д. И. Менделеев.

Векторы в пространства

Большинство понятий и утверждений для векторов непосредственно переносятся в стереометрию из планиметрии. Напомним основные положения соответствующей геометрической теории, подробно останавливаясь на тех из них, которые в пространстве выглядят иначе, чем на плоскости.

Определение и свойства векторов в пространстве

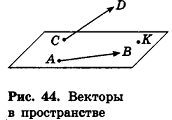
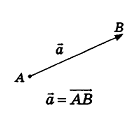
Как известно из курса геометрии 9 класса, вектором, называется направленный отрезок. Направление вектора (от начала к концу) на рисунках обозначают стрелкой. Вектор, начало и конец которого совпадают, называется нулевым. Нулевой вектор не имеет какого-либо определенного направления. На рисунке 44 изображены ненулевые векторы 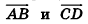и нулевой вектор .

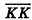Нулевой вектор часто обозначают .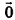

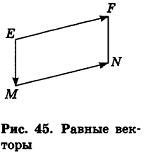
Так же как и на плоскости, ненулевой вектор в пространстве характеризуется не только направлением, но и длиной. Это позволяет рассматривать параллельный перенос в направлении луча АВ на расстояние, равное длине отрезка АВ, как параллельный перенос на вектор . В пространстве, как и на плоскости, равными векторами называются векторы, если они совмещаются параллельным переносом. На рисунке 45 изображены равные векторы , которые совмещаются параллельным переносом на вектор .

Так как положение точки в пространстве задается тремя координатами, дополняется определение координат вектора.

Определение:

Координатами вектора 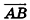с началом в точке 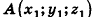и концом в точке 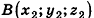называются числа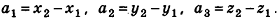

Соответственно длина (модуль) вектора 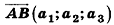вычисляется по формуле

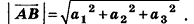
Нулевой вектор имеет нулевые координаты, и его длина равна нулю: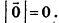

Так же как и на плоскости, в пространстве равные векторы имеют равные координаты, и наоборот: если у векторов соответствующие координаты равны, то эти векторы равны.

Напомним, что ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.

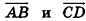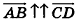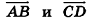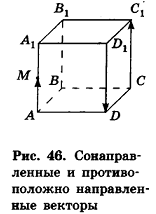
В свою очередь, среди коллинеарных векторов различают сонаправленные и противоположно направленные. Если лучи АВ и CD сонаправлены, то ненулевые векторы также сонаправлены (записывают ); если лучи АВ и CD противоположно направлены, то векторы также противоположно направлены (записывают 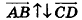). На рисунке 46 изображен куб 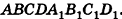. На этом рисунке векторы 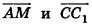сонаправлены, а векторы 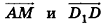противоположно направлены. Противоположно направленные векторы, длины которых равны, называются противоположными. На рисунке 46 такими являются, например, векторы 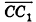и 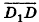(записывают ).

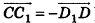Пример №5

Даны точки А (-7; 4; 2) и В(-2;0;-l). Найдите координаты кондов вектора 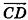, равного вектору 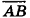, если точка С лежит на оси аппликат, а точка D — в плоскости Оху.

Решение:

Пусть 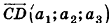. Так как 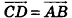, то 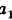= -2-(-7)=5, 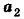=0-4 = -4, 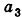= -1-2 = -3. Следовательно, 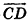(5;-4;-3). Учитывая условия расположения точек С и D, имеем: C(0;0;z), D(x;y;0), то есть 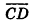(x;y;-z). Остюда х = 5, у = -4, z = 3.

Ответ: С(0;0;3), D(5;-4;0).

Операции над векторами в пространстве

Операции сложения и вычитания для векторов в пространстве определяют аналогично тому, как их вводили на плоскости. Итак, для векторов :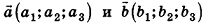

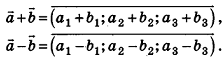
Так же сохраняются в пространстве и соответствующие свойства этих операций. Для любых векторов :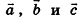

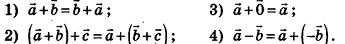
Доказательство утверждений 1-4 несложно получить с помощью геометрических построений аналогично тому, как это проводилось на плоскости.

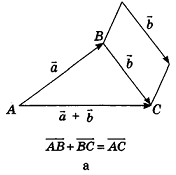
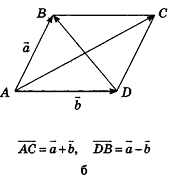
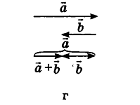
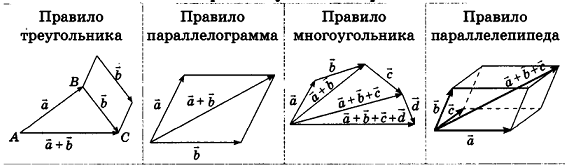
Для действий с неколлинеарными векторами в геометрической форме в пространстве, как и на плоскости, можно воспользоваться правилом треугольника (рис. 47, а) и правилом параллелограмма (рис. 47, б). Правила сложения двух коллинеарных векторов иллюстрирует рисунок 47, в, г.

Обобщением правила треугольника для сложения нескольких векторов является правило многоугольника (рис. 48, а). Особенность его применения в пространстве заключается в том, что векторы-слагаемые не обязательно принадлежат одной плоскости (то есть многоугольник, который получается при построении вектора-суммы, может быть пространственным). Например, на рисунке 48, б в тетраэдре РАВС получим векторное равенство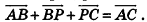

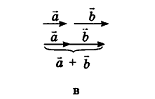
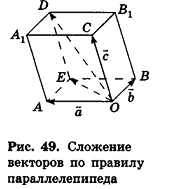
Опишем еще одно правило, которое служит для. сложения трех векторов в пространстве. Пусть векторы-слагаемые 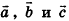при откладывании их от общего начала О не лежат в одной плоскости. Построим параллелепипед так, чтобы отрезки OA, OB и ОС, которые изображают векторы-слагаемые, были его ребрами (рис. 49). Тогда, используя правило параллелограмма, получаем 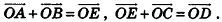Следовательно, 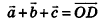, то есть вектор-сумма изображается диагональю параллелепипеда, построенного на векторах-слагаемых. Это правило сложения векторов представляет собой пространственный аналог правила параллелограмма и называется правилом параллелепипеда.

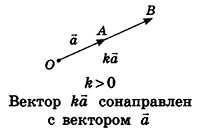
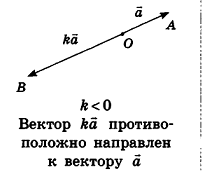
Произведением вектора 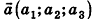на число k (или произведением числа k на вектор а) в пространстве называют вектор 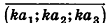, который обозначают 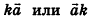. Если 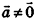, то вектор 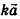сонаправлен с вектором а при условии k>0 и противоположно направлен вектору а при условии k<0, причем при любом значении 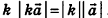. В частности, 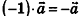, где 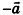— вектор, противоположный вектору a.

Основные свойства умножения вектора на число, известные из курса планиметрии, в стереометрии сохраняются. Для любых векторов 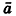и 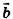и чисел :

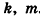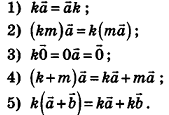
Доказательство утверждений 1-5 аналогично случаю на плоскости. Докажем, например, утверждение 4. Пусть дан вектор 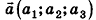. Тогда, по определению произведения вектора на число и суммы векторов, имеем:

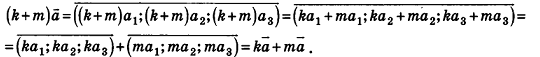
В пространстве сохраняется также необходимое и достаточное условие коллинеарности векторов: если — коллинеарные векторы, то существует число k такое, что , и наоборот: если для ненулевых векторов 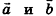выполняется равенство 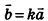, то векторы 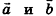коллинеарны.

При решении задач векторное равенство 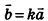для векторов 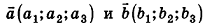часто применяют в координатной форме:

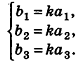
Если данные векторы не имеют нулевых координат, удобнее использовать пропорциональные соотношения

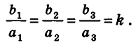
В пространстве, как и на плоскости, необходимым и достаточным условием принадлежности точек А, В и С одной прямой является коллинеарность векторов 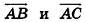. Рассмотрим еще одно векторное условие принадлежности точек А, В и С одной прямой.

Пример №6

(условие принадлежности трех точек одной прямой)

Если точки А, В и С лежат на одной прямой, то для любой точки пространства О выполняется векторное равенство 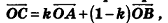где к — некоторое число. Докажите.

Решение:

Так как точки А, В и С лежат на одной прямой, то векторы 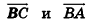коллинеарны, то есть существует число k такое, что 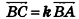. Учитывая, что 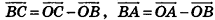, имеем:

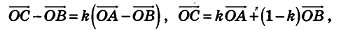
что и требовалось доказать.

Скалярное произведение векторов, в пространстве

Скалярным произведением векторов 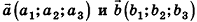называется число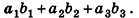

Обычно скалярное произведение векторов 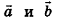обозначают 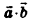или .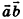

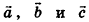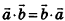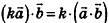Свойства скалярного произведения векторов, известные из курса планиметрии, в пространстве сохраняются. Для любых векторов и числа k: 1) ; 2) ; 3).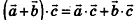

Доказательство утверждений 1-3 аналогично случаю на плоскости. Докажем, например, утверждение 3. Пусть даны векторы 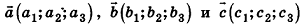. Тогда, по определению скалярного произведения, имеем:

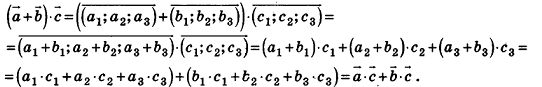
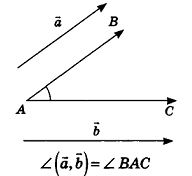
В пространстве углом между ненулевыми векторами называют угол ВАС, а углом Между произвольными ненулевыми векторами — угол между векторами, которые равны данным векторам и имеют общее начало (рис. 50).

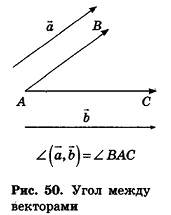
Точно так же как и на плоскости, в пространстве доказывают, что скалярное произведение векторов равно произведению их длин на косинус угла между ними. Таким образом, 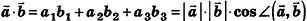. Отсюда следует, что скалярный квадрат вектора а равен квадрату его длины: 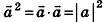. Сохраняется также необходимое и достаточное условие перпендикулярности двух векторов: если 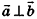, то 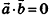, и наоборот: если для ненулевых векторов a и b выполняется равенство a .

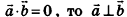Пример №7

Докажите с помощью векторов, что прямая, перпендикулярная двум сторонам треугольника, перпендикулярна и третьей его стороне.

Решение:

Пусть прямая MN перпендикулярна сторонам АВ и ВС треугольника ABC (рис. 51). Докажем, что 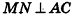. По свойству перпендикулярных векторов 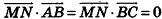. Так как 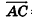=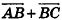, то 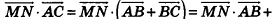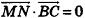. Следовательно, по признаку перпендикулярности векторов векторы 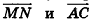а значит, прямые MN и АС перпендикулярны.

Свойства векторов широко применяются в физике и технике, где исследователям часто приходится рассматривать пространственные векторные величины — силу, скорость, перемещение и др. Например, электрический ток, направление которого задано вектором 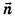, образует магнитное поле, которое в каждой точке пространства характеризуется вектором магнитной индукции 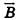(рис. 52).

Применение метода координат и векторов к решению стереометрических задач

Рассматривая векторы на плоскости, мы уделяли особое внимание коллинеарным векторам — векторам, которые при условии откладывания их от одной и той же точки лежат на одной прямой. В пространстве важную роль играют векторы, которые при условии откладывания их от одной точки лежат в одной плоскости.

Компланарные векторы. Разложение вектора по трем компланарным векторам

Определение:

Векторы называются компланарными, если при откладывании их от одной и той же точки они лежат в одной плоскости.

Из определения компланарных векторов следует, что направленные отрезки, изображающие компланарные векторы, лежат в одной плоскости или в параллельных плоскостях.

Очевидно, что любые два вектора компланарны. Компланарными являются также три вектора, среди которых хотя бы один нулевой, и три вектора, среди которых хотя бы два коллинеарны. Данные утверждения следуют непосредственно из определения (объясните почему).

На рисунке 56 изображен куб 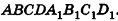. Векторы 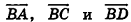компланарны, так как отрезки ВА, ВС и BD лежат в одной плоскости; векторы ВА, ВС и B1D1 также компланарны, так как отрезки 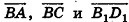лежат в параллельных плоскостях Векторы не компланарны, так как отрезки ВА, ВС и ВВ1 не лежат ни в одной плоскости, ни в параллельных плоскостях.

Пример №8 (признак компланарности трех векторов)

Если вектор 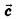можно разложить по векторам 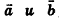, то есть представить в ви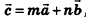де , где 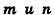— некоторые числа, то векторы 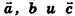компланарны. Докажите.

Решение:

Если векторы 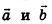коллинеарны, то компланарность векторов 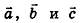очевидна.

Пусть векторы 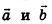не коллинеарны. Отложим от произвольной точки пространства О векторы 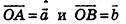(рис. 57). Очевидно, что эти векторы, как и прямые OA и ОВ, лежат в одной плоскости. В этой же плоскости лежат векторы 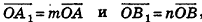, а значит, и их сумма — вектор 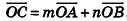, равный вектору с. Итак, векторы 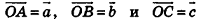лежат в одной плоскости, то есть векторы 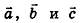компланарны.

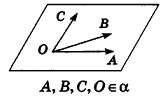
Заметим, что полученное векторное соотношение 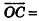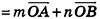можно рассматривать как условие принадлежности точки О плоскости ABC.

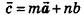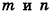Напомним: в 9 классе было доказано, что на плоскости для любого вектора с существует единственное представление в виде , где — некоторые числа, 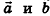— фиксированные неколлинеарные векторы (такое представление называют разложением вектора с по векторам ).

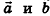В отличие от плоскости, в пространстве вектор не всегда можно разложить по двум неколлинеарным векторам, но всегда можно разложить по трем некомпланарным векторам.

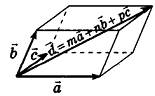
Теорема (о разложении вектора по трем некомпланарным векторам)

Любой вектор d можно разложить по трем некомпланарным векторам 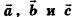, то есть представить в ви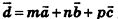де , где 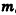, 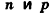— некоторые числа, причем такое разложение единственно.

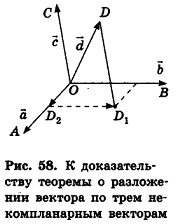
Доказательство:

Отложим от произвольной точки пространства О векторы 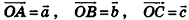и 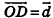. Проведем через точку D прямую, параллельную ОС. Она пересечет плоскость АОВ в некоторой точке 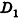Рассмотрим случай, когда точка не принадлежит ни одной из прямых OA и ОВ (рис. 58). Проведем через точку 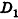прямую, параллельную ОВ. Она пересечет прямую OA в некоторой точке 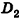. По правилу многоугольника:

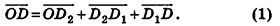
Но 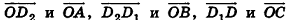— пары коллинеарных векторов, значит, существуют числа т, п и р такие, что 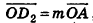, 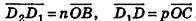. Подставив эти выражения в равенство (1), получим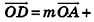 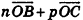, то есть

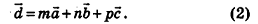
Другие случаи расположения точки 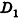относительно плоскости АОВ рассмотрите самостоятельно.

Докажем теперь единственность разложения (2) методом от противного. Допустим, что существует другой набор чисел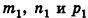

для которых имеет место равенство 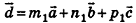. Вычитая это равенство из равенства (2), получим .

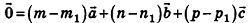Покажем, что полученное равенство выполняется только в случае, когда 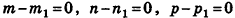. Действительно, если, например, 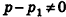, то тогда 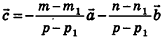Отсюда по признаку компланарности векторов следует, что векторы 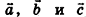компланарны, но это противоречит условию теоремы. Следовательно, наше предположение неверно, и 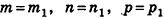Таким образом, разложение (2) единственно.

Доказанная теорема имеет широкое практическое применение. Например, некоторые космические корабли (рис. 59) оснащены тремя блоками двигателей, позволяющими двигаться вдоль трех некомпланарных векторов. Управляя их взаимодействием, корабль в пространстве можно перемещать в любом направлении.

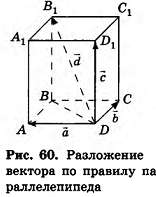
Отметим также связь доказанной теоремы с правилом параллелепипеда. На рисунке 60 диагональ DB_l параллелепипеда изображает сумму трех векторов: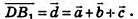

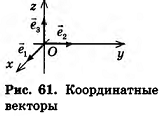
Данная теорема применяется и в прямоугольной системе координат: вектор 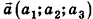часто раскладывают по единичным векторам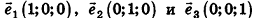, сонаправленным с осями координат. Эти единичные векторы называют координатными векторами или ортами (рис. 61). Нетрудно доказать, что коэффициенты такого разложения равны координатам вектора а, то есть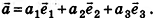

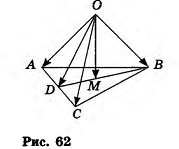
Пример №9 (о точке пересечения медиан треугольника)

Если М — точка пересечения медиан треугольника АВС, О — произвольная точка пространства, то 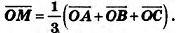Докажите.

Решение:

Пусть BD — медиана треугольника ABC (рис. 62). По свойству точки пересечения медиан треугольника 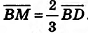. Тогда

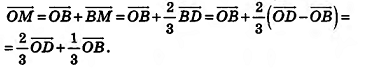
Так как 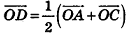(объясните почему), то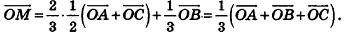

Пример №10

В параллелепипеде диагонали грани пересекаются в точке О (рис. 63). Разложите вектор 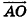по векторам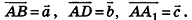

Решение:

По правилу треугольника 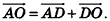Так как 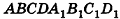— параллелепипед, то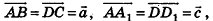

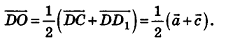
Отсюда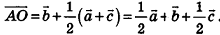

Ответ: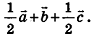

Векторный и координатный методы в пространстве

Так же как и на плоскости, в пространстве использование векторов и векторных соотношений во многих случаях упрощает рассуждения и расчеты в задачах и теоремах.

Применение векторного метода предусматривает три основных этапа:

1. сформулировать задачу на «языке векторов» — для этого необходимо рассмотреть векторы, связанные с данными отрезками, и составить соответствующие условию задачи векторные равенства;
2. преобразовать составленные равенства, воспользовавшись известными векторными соотношениями;
3. перевести полученные результаты на «язык геометрии».

Для перевода геометрических соотношений на «язык векторов» и наоборот обобщим некоторые результаты, полученные в теоремах и задачах 9 и 11 классов, в приведенной ниже таблице.

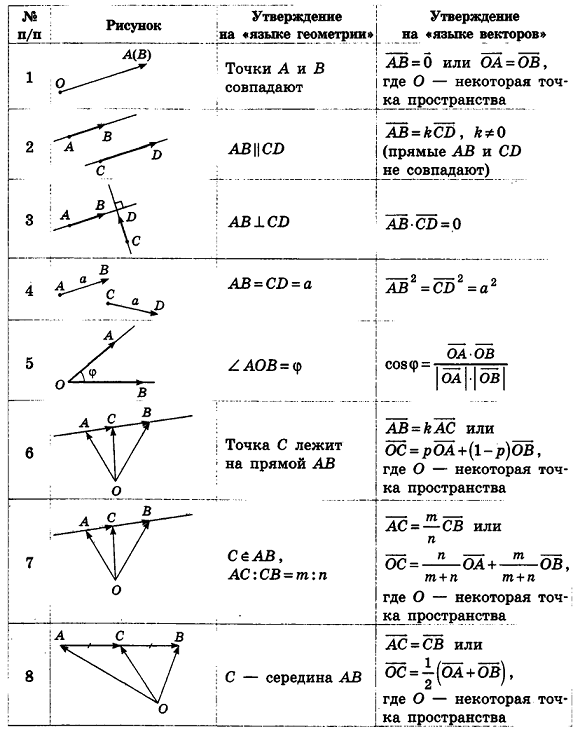
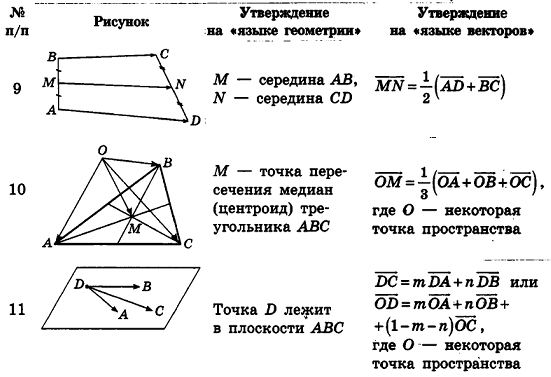
Рассмотрим сначала пример применения векторного метода для доказательства уже известного стереометрического факта.

Пример №11

Докажите с помощью векторов признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум прямым, которые лежат в плоскости и пересекаются, то она перпендикулярна данной плоскости.

Решение:

Пусть 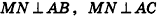(рис. 64). Докажем, что .

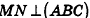По признаку перпендикулярности прямой и плоскости необходимо доказать, что прямая MN перпендикулярна любой прямой

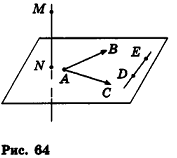
плоскости ABC. Пусть DE — произвольная прямая плоскости ABC. Докажем, что 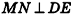, то есть .

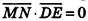Так как векторы 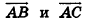не коллинеарны, то любой вектор плоскости ABC можно разложить по этим векторам, то есть существуют числа тип такие, что 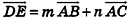. Поэтому

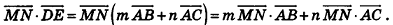
По условию задачи 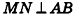, , 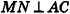следовательно, 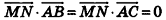, откуда 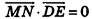. Таким образом, прямая MN перпендикулярна любой прямой плоскости ABC, то есть по признаку .

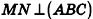В ходе решения задач векторный метод часто объединяют с методом координат. Напомним, что решение геометрической задачи методом координат также состоит из трех основных этапов:

1. задать систему координат и сформулировать данную задачу на «языке координат»;
2. преобразовать алгебраические выражения, воспользовавшись известными соотношениями и формулами;
3. перевести полученный результат на «язык геометрии».

Обычно на первом этапе решения систему координат выбирают так, чтобы как можно больше координат вершин рассматриваемой фигуры были равны нулю или одному и тому же числу — это позволяет максимально упростить дальнейшие алгебраические преобразования. Методом координат в пространстве удобнее пользоваться тогда, когда элементами данной фигуры являются три взаимно перпендикулярных отрезка с общим кондом. В таком случае систему координат целесообразно вводить так, чтобы эти отрезки лежали на осях координат.

Пример №12

Найдите угол между скрещивающимися прямыми, одна из которых содержит диагональ куба, а вторая — диагональ его грани.

Решение:

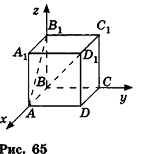
Разместим куб 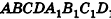с ребром а в системе координат так, как показано на рисунке 65, и найдем угол между прямыми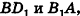

воспользовавшись формулой скалярного произведения векторов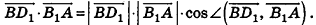

Так как 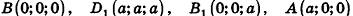, то .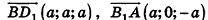

Следовательно, 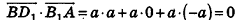, то есть данные векторы перпендикулярны, и искомый угол равен 90°.

Ответ: 90°.

Справочный материал

Декартовы координаты в пространстве

Движения в пространстве

Движением, называется преобразование одной фигуры в другую, при котором сохраняются расстояния между точками.

Две фигуры называются равными, если они переводятся одна в другую движением

Движение в пространстве переводит прямые в прямые, отрезки — в равные отрезки, углы — в равные углы, плоскости — в плоскости.

Преобразование подобия в пространстве

Преобразованием подобия (подобием) называется такое преобразование фигуры F в фигуру F', при котором расстояния между точками изменяются в одном и том же отношении k ( k > 0) Число k>0 называют коэффициентом подобия, а фигуры F и F' — подобными

Преобразование подобия переводит прямые в прямые, отрезки — в отрезки, плоскости — в плоскости, а также сохраняет углы между лучами X'Y' = kXY

Гомотетией с центром в точке О и коэффициентом k (k>0) называется такое преобразование фигуры F в фигуру F', при котором каждая точка X фигуры F переходит в точку X' фигуры F, лежащую на луче ОХ, и ОХ' = кОХ

Число k называют коэффициентом гомотетии, а фигуры F и F' — гомотетичными

Основное свойство гомотетии: гомотетия является преобразованием подобия

Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя

Векторы

Вектором называется направленный отрезок

Координатами вектора с началом в точке и концом в точке называются числа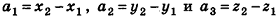

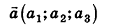
Длина (модуль) вектора 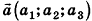вычисляется по формуле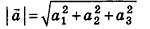

Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых

Векторы сонаправлены

Векторы 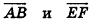противоположно направлены

Противоположными векторами называются два противоположно направленных вектора одинаковой длины

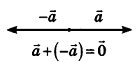
Два вектора называются равными, если они совмещаются параллельным переносом

От любой точки можно отложить вектор, равный данному, и притом только один Критерии равных векторов:

1. векторы сонаправлены и имеют равные длины;
2. векторы имеют равные координаты

Операции с векторами

Сложение векторов

Суммой векторов 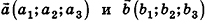называется вектор 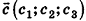с координатами 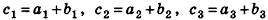, то есть

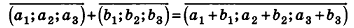
Построение суммы векторов

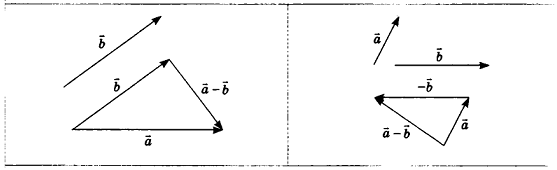
Вычитание векторов

Разностью векторов называется такой вектор , сумма которого с вектором b равна вектору а, то есть :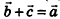

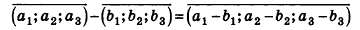
Построение разности векторов

Умножение вектора на число

Произведением вектора 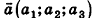на число k (или произведением числа k на вектор а) называется вектор 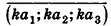, который обозначают ka или ak :

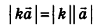
Если — коллинеарные векторы, то существует число k такое, что 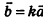, и наоборот: если для ненулевых векторов 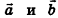выполняется равенство 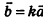, то векторы 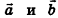коллинеарны

У коллинеарных векторов соответствующие координаты пропорциональны, и наоборот: если у двух векторов соответствующие координаты пропорциональны, то эти векторы коллинеарны

Скалярное произведение векторов

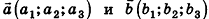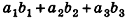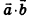Скалярным произведением векторов называется число . Обычно скалярное произведение векторов обозначают или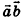

Скалярное произведение 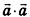называется скалярным квадратом вектора :

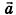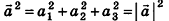
Скалярное произведение векторов равно произведению их длин на косинус угла между ними: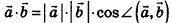

Свойство и признак перпендикулярных векторов: если 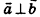, то 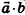= 0, и наоборот: если для ненулевых векторов 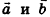выполняется равенство 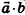= 0, то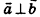

Компланарные векторы

Ненулевые векторы называются компланарными, если при откладывании их от одной и той же точки они лежат в одной плоскости

Любой вектор d можно разложить по трем некомпланарным векторам 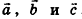, то есть представить в виде 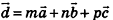, где m, 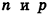— некоторые числа, причем такое разложение единственно

Историческая справка

Эпоха великих географических открытий и обусловленное ими развитие производства, торговли, мореплавания стали толчком к возникновению аналитической геометрии. Этот раздел геометрии, основанный на введении прямоугольных координат и установлении соответствия между алгебраическими уравнениями и геометрическими фигурами, стал итогом многолетних математических исследований.

Создателями аналитической геометрии считают французских ученых Рене Декарта (1696-1650) и Пьера Ферма (1601-1665). Ферма в начале XVII века, занимаясь восстановлением утраченных работ древнегреческих ученых, в частности Аполлония Пергского, определил общий подход к изучению геометрических мест точек через алгебраические уравнения. Открытие Декартом системы координат на плоскости позволило создать математический аппарат для воплощения идей аналитической геометрии. Но как Ферма, так и Декарт только говорили о возможности использования координат в пространстве. Трехмерную систему координат первым начал применять французский математик Алексис Клод Клеро (1713-1765), а систематическое изложение аналитической геометрии в пространстве представил в 1748 году выдающийся ученый Леонард Эйлер.

В историю аналитической геометрии вписаны также имена украинских ученых. Уроженец Винни-чины Виктор Яковлевич Буняковский (1804-1889) учился математике в Париже, у ведущих ученых своего времени — Коши, Лежандра, Пуассона, Лапласа, а позднее работал в Петербурге. Он был автором около ста работ по математическому анализу, алгебре, геометрии, теории чисел и теории вероятностей. Так, известное вам неравенство а-6<|а|-|&| является векторным представлением математического факта, обобщенного Буняковским на основании идей его учителя Коши, и получило название «неравенство Коши — Буняковского».