
Действия с корнями нечетной степени с примерами решения
Содержание:
Теорема:
Пусть 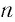
1) При любых значениях 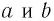

2) При любых значениях 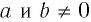 верно равенство
верно равенство

3) при любых значениях 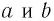 верно равенство
верно равенство

Доказательство:
Легко убедиться, что выражения, входящие в равенства (1)—(3), имеют смысл. Эти равенства, очевидно, верны при 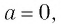 а равенства (1) и (3) — и при
а равенства (1) и (3) — и при 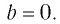 Поэтому доказательства проводятся при
Поэтому доказательства проводятся при 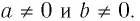
Докажем утверждение 1). Возведем левую и правую части равенства (1) в 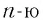 степень:
степень:
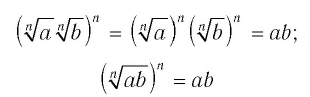
(поясните каждое равенство).
Тогда 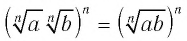 и согласно следствию из п. 1.1 имеем
и согласно следствию из п. 1.1 имеем 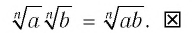
Тождества (2) и (3) из утверждений 2), 3) теоремы доказываются аналогично (докажите их самостоятельно). ▲
Утверждение 1) теоремы можно сформулировать и так:
Пусть 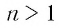 — нечетное число. Корень
— нечетное число. Корень 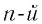 степени из произведения двух чисел равен произведению корней
степени из произведения двух чисел равен произведению корней 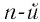 степени из этих чисел.
степени из этих чисел.
Такая же теорема верна при любом числе перемножаемых корней (доказывается она совершенно аналогично).
Пусть 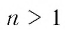 — нечетное число. Корень
— нечетное число. Корень 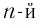 степени из произведения нескольких чисел равен произведению корней
степени из произведения нескольких чисел равен произведению корней 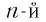 степени из этих чисел.
степени из этих чисел.
Таким образом, при любых значениях 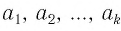 верно равенство
верно равенство
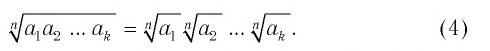
В частности, полагая в этом равенстве 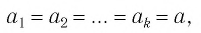 получим
получим

Утверждение 2) теоремы можно сформулировать так:
Пусть 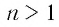 — нечетное число. Корень
— нечетное число. Корень 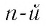 степени из дроби равен частному от деления корня
степени из дроби равен частному от деления корня 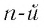 степени из числителя на корень
степени из числителя на корень 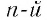 степени из знаменателя.
степени из знаменателя.
Преобразование выражения 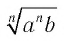 к виду
к виду 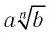 (в утверждении 3) теоремы) называется вынесением множителя из-под знака корня нечетной степени.
(в утверждении 3) теоремы) называется вынесением множителя из-под знака корня нечетной степени.
Преобразование выражения 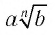 к виду
к виду 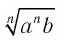 называется внесением множителя под знак корня нечетной степени.
называется внесением множителя под знак корня нечетной степени.
Заметим, что каждое из равенств (1)—(5) является тождеством.
Примеры с решением
Пример №1
Найти значение выражения 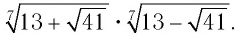
Решение:
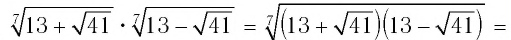
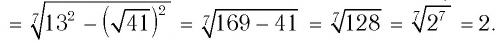
Пример №2
Вынести множитель из-под знака корня:
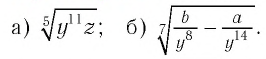
Решение:
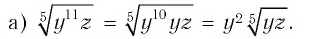
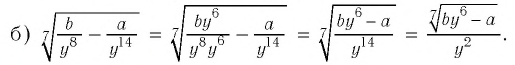
Пример №3
Внести множитель под знак корня:
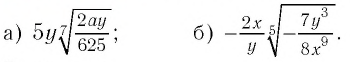
Решение:
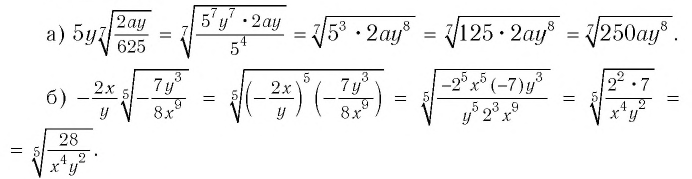
Пример №4
Освободиться от иррациональности в знаменателе:
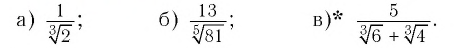
Решение:
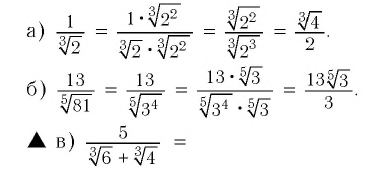
используем формулу 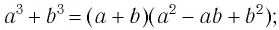 домножим числитель и знаменатель на неполный квадрат разности выражений
домножим числитель и знаменатель на неполный квадрат разности выражений 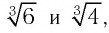 т. е. на выражение
т. е. на выражение 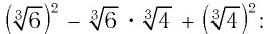
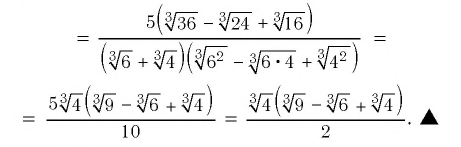
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |