
Действительные числа - определение и вычисление с примерами решения
Содержание:
Действительные числа
В основе применения математических методов при решении практических задач лежат вычисления и измерения. При счете используются натуральные числа. При делении целого на части натуральных чисел недостаточно. Поэтому вводятся дробные числа. Длину отрезка можно выразить с помощью рационального числа с любой точностью. В теоретических вычислениях приходится рассматривать отрезки, длины которых не выражаются с помощью рациональных чисел. По этой причине вводится понятие иррационального числа. Изменение значений величины в противоположном направлении удобнее показать отрицательными числами.
Действительные числа
Рациональные и иррациональные числа образуют множество действительных чисел. Любое действительное число можно представить в виде бесконечной десятичной дроби. Для любого действительного числа 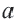
Два действительных числа, отличающиеся только знаками, называются противоположными числами. 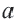 и -
и -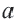 взаимно противоположные числа. Сумма двух противоположных чисел равна нулю:
взаимно противоположные числа. Сумма двух противоположных чисел равна нулю: 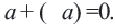 При
При 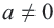 ,
, 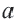 и
и 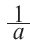 являются взаимно обратными числами. Произведение двух взаимно обратных чисел равно единице:
являются взаимно обратными числами. Произведение двух взаимно обратных чисел равно единице: 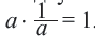 . Сумма, разность, произведение и отношение (делитель отличен от 0) двух действительных чисел является действительным числом. Каждой точке числовой оси соответствует одно определенное действительное число и, наоборот, каждое действительное число можно изобразить единственной точкой на числовой оси.
. Сумма, разность, произведение и отношение (делитель отличен от 0) двух действительных чисел является действительным числом. Каждой точке числовой оси соответствует одно определенное действительное число и, наоборот, каждое действительное число можно изобразить единственной точкой на числовой оси.
Для любых действительных чисел 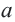 и
и 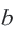 верно только одно из соотношений:
верно только одно из соотношений: 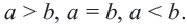 На числовой оси число, соответствующее точке, расположенной правее, больше числа, соответствующего точке, расположенной левее. Между двумя действительными числами существует бесконечное число действительных чисел. Наибольшее целое число, не превосходящее данное число, называется целой частью этого числа.
На числовой оси число, соответствующее точке, расположенной правее, больше числа, соответствующего точке, расположенной левее. Между двумя действительными числами существует бесконечное число действительных чисел. Наибольшее целое число, не превосходящее данное число, называется целой частью этого числа.
Абсолютная величина действительного числа показывает расстояние на числовой оси от точки, соответствующей этому числу, до начала отсчета.
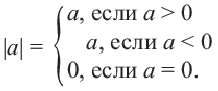
Расстояние между двумя точками числовой оси равно абсолютной величине разности их координат 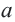 и
и 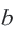 то есть,
то есть,  Обратите внимание на то, что
Обратите внимание на то, что 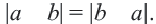
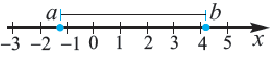
Действительные (вещественные числа)
Числа рациональные и иррациональные, положительные и отрицательные, получили название действительных или вещественных чисел. Геометрически действительные числа изображаются точками числовой оси - прямой, на которой указано положительное направление, масштаб и начальная точка (т.е. точки, изображающие 0 и 1).
Комплексные числа. Однако не успело ещё закрепиться новое расширенное понятие числа, как в процессе развития математики обнаружилось, что и новое понятие является также неудовлетворительным. В частности, решение квадратных уравнений уже на самой ранней ступени развития алгебры привело в области действительных чисел операции извлечения корня из отрицательного числа. Выяснилось, что среди действительных чисел нет ни одного такого, квадрат которого был бы величиной отрицательной, следовательно, и корень
квадратный из отрицательной величины 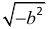 не может быть выражен никаким действительным числом.
не может быть выражен никаким действительным числом.
Мнимое число имеет вид 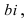 где
где 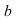 - действительное число, а i - «мнимая единица», определяемая равенством
- действительное число, а i - «мнимая единица», определяемая равенством 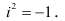 Выражение
Выражение 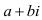 называется комплексным числом. Комплексные числа введены в алгебру в середине 16-го в. в связи с решением кубического уравнения. С конца 17-го в. они применяются и в математическом анализе.
называется комплексным числом. Комплексные числа введены в алгебру в середине 16-го в. в связи с решением кубического уравнения. С конца 17-го в. они применяются и в математическом анализе.
Абсолютная величина действительного числа
Абсолютной величиной (или модулем) действительного числа х (обозначается |х|) называется неотрицательное действительное число,
удовлетворяющее условиям:
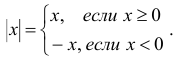
Свойства абсолютных величин:
1. 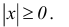
2. 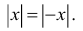
3. 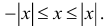
4. Пусть 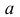 - положительное число, тогда неравенства
- положительное число, тогда неравенства 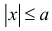 и
и 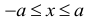 равносильны.
равносильны.
5. Для любых двух действительных чисел справедливы неравенства 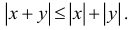
6. Для любых двух действительных чисел справедливы неравенства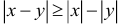
7. 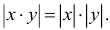
8. 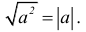
9. 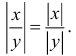
Постоянные и переменные величины
Постоянной величиной называется величина, численные значения которой не меняются.
Величина с одним и тем же названием может быть постоянной (скорость равномерного движения) или переменной (скорость равномерно ускоренного движения).
Величины, которые сохраняют своё значение в любом явлении, называются абсолютными постоянными, например число 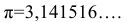
Переменной величиной называется величина, которая принимает различные числовые значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой величины.
Промежутком или открытым интервалом (а,b) называется совокупность всех чисел х, заключенных между данными числами 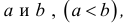 причем сами эти числа не принадлежат рассматриваемой совокупности чисел
причем сами эти числа не принадлежат рассматриваемой совокупности чисел 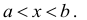
Отрезком или закрытым интервалом 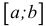 называется совокупность всех чисел х, заключенных между данными числами
называется совокупность всех чисел х, заключенных между данными числами 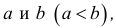 причем оба эти числа принадлежат рассматриваемой совокупности чисел
причем оба эти числа принадлежат рассматриваемой совокупности чисел 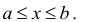
Естественным образом определяются полуоткрытые интервалы, т.е. промежутки, открытые с одной стороны. Например: 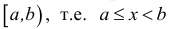 или
или 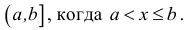
Определения интервалов можно сформулировать, используя вместо понятия «число» понятие «точка».
Окрестностью данной точки 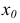 называется произвольный интервал
называется произвольный интервал 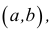 содержащий эту точку внутри себя.
содержащий эту точку внутри себя.
--------------
Действительные числа
Число является одной из основных математических абстракций, изучению которой может быть посвящен самостоятельный курс. Из многих концепций построения множества действительных чисел приведем аксиоматическую.
Определение 1.17. Множество R называется множеством вещественных чисел, а его элементы — вещественными (действительными) числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:
1. Аксиомы сложения
Определено отображение (операция сложения: + ), действующее из 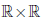 в
в  , которое каждой упорядоченной паре (x, y) элементов x, y из
, которое каждой упорядоченной паре (x, y) элементов x, y из  ставит в соответствие некоторый элемент x + y ∈
ставит в соответствие некоторый элемент x + y ∈  , называемый суммой x и y . При этом выполняются условия:
, называемый суммой x и y . При этом выполняются условия:
(a) x + y = y + x, ∀x, y ∈  (коммутативность сложения);
(коммутативность сложения);
(b) в  существует нейтральный элемент, называемый нулем, обозначаемый 0, такой, что x + 0 = x, ∀x ∈
существует нейтральный элемент, называемый нулем, обозначаемый 0, такой, что x + 0 = x, ∀x ∈  ;
;
(c) для любого элемента x ∈  в
в  существует элемент, называемый противоположным к x, обозначаемый (-x), такой, что x + (-x) = 0;
существует элемент, называемый противоположным к x, обозначаемый (-x), такой, что x + (-x) = 0;
(d) x + (y + z) = (x + y) + z, ∀x, y, z ∈ 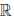 (ассоциативность сложения).
(ассоциативность сложения).
2. Аксиомы умножения
Определено отображение (операция умножения: •), действующее из 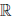 ×
× 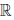 в
в 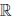 , которое каждой упорядоченной паре (x, y) элементов x, y из
, которое каждой упорядоченной паре (x, y) элементов x, y из 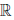 ставит в соответствие некоторый элемент x ∙ y ∈
ставит в соответствие некоторый элемент x ∙ y ∈ 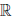 , называемый произведением x и y . При этом выполняются условия:
, называемый произведением x и y . При этом выполняются условия:
(a) x ∙ y = y ∙ x, ∀x,y ∈ 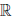 (коммутативность умножения);
(коммутативность умножения);
(b) в 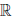 \{0} существует нейтральный элемент, называемый единицей, обозначаемый 1, такой, что 1 ∙ x = x, ∀x ∈
\{0} существует нейтральный элемент, называемый единицей, обозначаемый 1, такой, что 1 ∙ x = x, ∀x ∈ 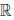 ;
;
(c) для любого элемента x ∈ 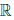 \{0} существует в
\{0} существует в 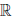 \ {0} обратный элемент, обозначаемый 1/x или x-1, такой, что x ∙ (1/x) = 1;
\ {0} обратный элемент, обозначаемый 1/x или x-1, такой, что x ∙ (1/x) = 1;
(d) x ∙ (y ∙ z) = (x ∙ y) ∙ z, ∀x,y,z ∈  (дистрибутивность умножения). Операции сложения и умножения связаны условием:
(дистрибутивность умножения). Операции сложения и умножения связаны условием:
(e) (x + y) ∙ z = x ∙ z + y ∙ z, ∀x,y., z ∈ 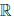 (дистрибутивность умножения по отношению к сложению).
(дистрибутивность умножения по отношению к сложению).
Множество, на котором определены обе операции, и которые удовлетворяют группам аксиом 1 и 2, называется алгебраическим полем.
(Часто знак операции умножения в математических выражениях опускают и вместо x ∙ y пишут xy.)
3. Аксиомы порядка
Для любых элементов x, y ∈ 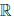 определено отношение
определено отношение  , то есть либо x
, то есть либо x  y, либо y
y, либо y  x. При этом выполняются условия:
x. При этом выполняются условия:
(a) x  x, ∀x ∈
x, ∀x ∈  ;
;
(b) если x, y ∈  таковы, что x
таковы, что x  y и y
y и y  x, то x = y;
x, то x = y;
(c) если x, y, z ∈  таковы, что x
таковы, что x  y и y
y и y  z, то x
z, то x  z (транзитивность);
z (транзитивность);
(d) если x, y, z ∈  и x
и x  y, то x + z
y, то x + z  y + z;
y + z;
(e) если x,y ∈  и 0
и 0  x, 0 6 y, то 0
x, 0 6 y, то 0  x ∙ y.
x ∙ y.
Отношение  называют отношением неравенства и читают: "не превосходит" или "меньше или равно". Множество, между элементами которого имеется отношение
называют отношением неравенства и читают: "не превосходит" или "меньше или равно". Множество, между элементами которого имеется отношение  , удовлетворяющее аксиомам 3, называется упорядоченным. Поэтому множество
, удовлетворяющее аксиомам 3, называется упорядоченным. Поэтому множество  является упорядоченным алгебраическим полем.
является упорядоченным алгебраическим полем.
4. Аксиома полноты (непрерывности)
Если X и Y — непустые подмножества множества  , обладающие тем свойством, что для любых элементов x ∈ X и y ∈ Y выполняется неравенство x
, обладающие тем свойством, что для любых элементов x ∈ X и y ∈ Y выполняется неравенство x  y, то существует такое число c, что
y, то существует такое число c, что
x  c
c  y, ∀x ∈ X, ∀y ∈ Y.
y, ∀x ∈ X, ∀y ∈ Y.
Эту аксиому часто называют принципом отделимости.
Можно доказать, что во введенном множестве R имеют место все, известные из школьного курса математики, свойства чисел. Желающие могут получить их самостоятельно или изучить соответствующий раздел в книгах [2] или [6].
Важнейшие подмножества действительных чисел
Определение 1.18. Множество X ⊂  называется множеством натуральных чисел, а его элементы — натуральными числами, если X — наименьшее числовое множество, которое содержит единицу и вместе с каждым элементом x содержит элемент x + 1.
называется множеством натуральных чисел, а его элементы — натуральными числами, если X — наименьшее числовое множество, которое содержит единицу и вместе с каждым элементом x содержит элемент x + 1.
Множество натуральных чисел обозначают через 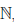 , а его произвольный элемент — через n. Число 1 + 1 ∈
, а его произвольный элемент — через n. Число 1 + 1 ∈ 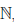 обозначают символом 2 и называют двойкой, число 2 + 1 обозначают символом 3 и называют тройкой и так далее. Можно доказать, что
обозначают символом 2 и называют двойкой, число 2 + 1 обозначают символом 3 и называют тройкой и так далее. Можно доказать, что
0  1
1 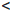 2
2 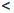 ∙∙∙
∙∙∙ 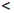 n
n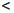 n + 1
n + 1  ... и
... и 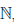 = {1, 2,...,n,n + 1,... }.
= {1, 2,...,n,n + 1,... }.
Прямым следствием определения 1.18 является принцип математической индукции.
Если подмножество E множества натуральных чисел 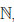 таково, что 1 ∈ E и вместе с числом x ∈ E множеству E принадлежит x + 1, то E =
таково, что 1 ∈ E и вместе с числом x ∈ E множеству E принадлежит x + 1, то E = 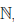 .
.
Иллюстрируя этот принцип в действии, докажем с его помощью формулу, называемую формулой бинома Ньютона:
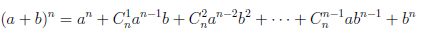
или коротко
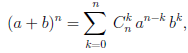 (1.1)
(1.1)
В этой формуле a, b — произвольные действительные числа, n — произвольное натуральное число,
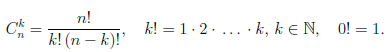
Пусть E — множество тех натуральных чисел n, для которых справедлива формула (1.1). При 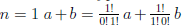 , что соответствует формуле (1.1). Поэтому n = 1 ∈ E.
, что соответствует формуле (1.1). Поэтому n = 1 ∈ E.
Покажем, что если n ∈ E , то n + 1 ∈ E :
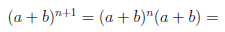
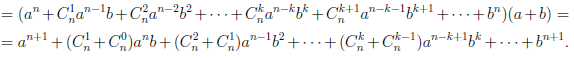
Но 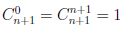 и при k = 1,2,3...n,
и при k = 1,2,3...n,
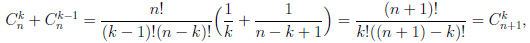
поэтому
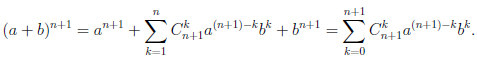
Таким образом, n + 1 ∈ E и, следовательно, E =  .
.
Числа 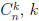 = 0, 1, 2, . . . n, называют биномиальными коэффициентами. Из формулы (1.1) следует, что
= 0, 1, 2, . . . n, называют биномиальными коэффициентами. Из формулы (1.1) следует, что
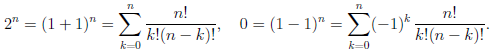
Определение 1.19. Множество, состоящее из всех натуральных чисел, им противоположных и нуля называют множеством целых чисел и обозначают символом Z.
Определение 1.20. Множество {m/n ∈  | m ∈
| m ∈ 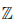 , n ∈
, n ∈ 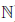 } называют множеством рациональных чисел и обозначают через
} называют множеством рациональных чисел и обозначают через 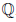 . Элемент
. Элемент 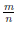 множества
множества 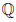 называют рациональным числом.
называют рациональным числом.
Можно доказать, что 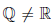 (например, можно доказать, что в
(например, можно доказать, что в 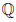 не существует числа s такого, что s ∙ s = 2).
не существует числа s такого, что s ∙ s = 2).
Определение 1.21. Действительные числа, которые не являются рациональными, называются иррациональными.
Часто полезна "геометрическая терминология в которой множество 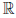 называют числовой прямой, его элементы — точками числовой прямой.
называют числовой прямой, его элементы — точками числовой прямой.
Пусть a, b ∈  и a
и a 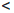 b, то есть a
b, то есть a  b и a
b и a 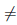 b. Введем следующие обозначения и названия для перечисленных ниже числовых множеств:
b. Введем следующие обозначения и названия для перечисленных ниже числовых множеств:
[a, b] := {x ∈  | a
| a  x
x  y} — отрезок ab (или сегмент ab);
y} — отрезок ab (или сегмент ab);
(a, b) := {x ∈  | a
| a 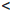 x
x 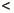 b} — интервал ab;
b} — интервал ab;
(a, b] := {x ∈  | a
| a 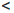 x
x  b} — полуинтервал ab, содержащий b;
b} — полуинтервал ab, содержащий b;
[a, b) := {x ∈  | a
| a  x
x 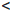 b} — полуинтервал ab, содержащий a.
b} — полуинтервал ab, содержащий a.
Введенные множества называют промежутками, числа a и b — их концами, число b - a — длиной промежутка.
Часто удобно дополнить множество  элементами, обозначаемыми символами +∞ и -∞, которые называют соответственно плюс бесконечность и минус бесконечность. При этом считают, если a ∈ R, что
элементами, обозначаемыми символами +∞ и -∞, которые называют соответственно плюс бесконечность и минус бесконечность. При этом считают, если a ∈ R, что
-∞ 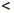 +∞; -∞
+∞; -∞ 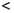 a
a 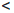 +∞,
+∞,
+∞ + (+∞) = +∞; a + (+∞) = +∞,
-∞ + (-∞) = -∞; a + (-∞) = -∞,
+∞ ∙ (+∞) = +∞, -∞ ∙ (-∞) = +∞,
±∞ ∙ a = ±∞, если a > 0,
±∞ ∙ a = ±∞, если a 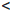 0.
0.
Множество  , дополненное символами +∞ и -∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается
, дополненное символами +∞ и -∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается  . Следующие множества (a ∈
. Следующие множества (a ∈  ) называют неограниченными промежутками:
) называют неограниченными промежутками:
[a, +∞) = {x ∈  | x ≥ a}, (a, +∞) = {x ∈
| x ≥ a}, (a, +∞) = {x ∈  | a
| a 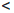 x},
x},
(-∞, a] = {x ∈  | x
| x a}, (-∞, a) = {x ∈
a}, (-∞, a) = {x ∈  | x
| x 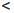 a},
a},
В этих обозначениях часто пишут:  = (-∞, +∞).
= (-∞, +∞).
------------------
Действительные числа
Определение действительного числа по Дедекинду
Одним из основных понятий, изучаемых в курсе математического анализа, является понятие действительного числа. Оно возникает в школьном курсе элементарной алгебры фактически на интуитивном уровне как развитие понятия о числе — от натуральных чисел к целым, от целых к рациональным, от рациональных к действительным. В нашу задачу не входит сейчас аккуратное выведение этой цепочки из основных представлений о натуральных числах и их свойствах. Будем считать, что понятие рационального числа и основные свойства рациональных чисел, а также другие вопросы школьного курса элементарной алгебры (в частности, основная символика теории множеств) хорошо известны. Напомним, что множество натуральных чисел обозначается N, множество целых чисел — Z. множество рациональных чисел — Q.
При переходе к действительным числам (множество которых обозначается R) возникает качественно новое понятие непрерывности, присущее именно математическому анализу Поэтому этот шаг будет разобран подробно и аккуратно.
Определение 1.1. Сечением а множества рациональных чисел Q называется такое разбиение Q на два непустых множества 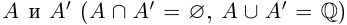 , что для всех
, что для всех 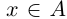
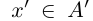 выполняется неравенство х < х'. Множество А называется нижним классом сечения, множество
выполняется неравенство х < х'. Множество А называется нижним классом сечения, множество 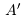 — верхним классом.
— верхним классом.
Применяется обозначение 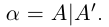
Приведём простейшие примеры сечений.
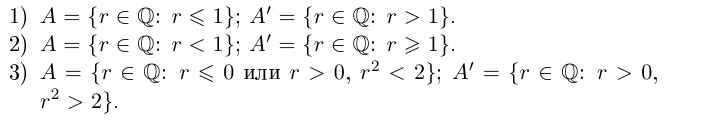
Напомним, что не существует рационального числа такого, что г2 = 2.
Легко видеть, что в примере 1) в нижнем классе А есть наибольший элемент в верхнем классе А' нет наименьшего элемента. В примере 2) в A нет наибольшего элемента, в А' есть наименьший. В примере 3) в A нет наибольшего элемента, в А' нет наименьшего.
Докажем, например, что в примере 3) в A нет наибольшего элемента (значком □ будем обозначать начало доказательства, значком ■ — конец доказательства).
□ Доказательство от противного. Пусть в А есть наибольший элемент г. Тогда г > 0, г2 < 2. Но легко заметить, что найдётся рациональное число 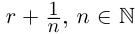 такое, что
такое, что 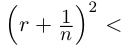 2. В самом деле, последнее неравенство равносильно г2
2. В самом деле, последнее неравенство равносильно г2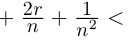 2, что заведомо выполняется при
2, что заведомо выполняется при 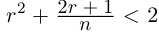 т.е. при
т.е. при 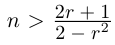 Для таких n число
Для таких n число 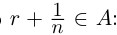 : это противоречит тому, что г — наибольший элемент в А. Значит, в А нет наибольшего элемента. ■
: это противоречит тому, что г — наибольший элемент в А. Значит, в А нет наибольшего элемента. ■
Докажем теперь, что невозможен случай, когда в А есть наибольший элемент, в А' есть наименьший.
□ Пусть существуют 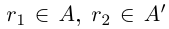 — соответственно наибольший и наименьший элементы в этих классах. Выберем рациональное число
— соответственно наибольший и наименьший элементы в этих классах. Выберем рациональное число 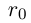 такое, что
такое, что 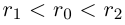 (например,
(например, 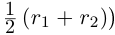 . Так как
. Так как 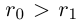 , то
, то 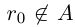 , так как
, так как 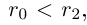 , то
, то 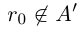 — это невозможно, так как любое рациональное число принадлежит либо А, либо А'.
— это невозможно, так как любое рациональное число принадлежит либо А, либо А'.
Итак, существуют сечения трёх типов.
I. В нижнем классе есть наибольший элемент, в верхнем нет наименьшего.
II. В нижнем классе нет наибольшего элемента, в верхнем есть наименьший.
III. В нижнем классе нет наибольшего элемента, в верхнем нет наименьшего.
Определение 1.2. Иррациональным числом называется сечением III типа.
В случаях I и II говорят, что сечение производится рациональным числом (соответствующим наибольшему элементу в нижнем классе или наименьшему в верхнем). Сечения I и II типов отождествляются с соответствующими рациональными числами. Чтобы соответствие было взаимно однозначным, сечения типа I в дальнейшем не рассматриваются.
Например, сечение в примере 1) мы не будем рассматривать. Сечение в примере 2) — это рациональное число 1. Сечение в примере 3) — это иррациональное число (которое естественно объявить корнем квадратным из 2, не придавая пока этому термину строгого смысла).
Определение 1.3. Действительным (вещественным) числом называется любое сечение II или III типов. Множество действительных чисел обозначается R. Сечения II типа отождествляются с соответствующими рациональными числами.
У сечений, соответствующих действительным числам, в нижнем классе нет наибольшего элемента. Если в верхнем классе есть наименьший элемент — сечение является рациональным числом, если нет — иррациональным.
Определение 1.4. Два действительных числа 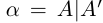
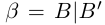 называются равными, если А = В, А' = В' (совпадают как множества, достаточно требовать только А = В).
называются равными, если А = В, А' = В' (совпадают как множества, достаточно требовать только А = В).
Определение 1.5. Рассмотрим два неравных действительных числа 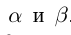 . Говорят, что
. Говорят, что 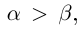 , если
, если 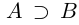 (т.е.
(т.е. 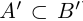 )
) 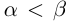 , если
, если 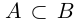 (т.е.
(т.е. 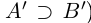 ; включения множеств считаются строгими.
; включения множеств считаются строгими.
Символ > читается «больше», символ < читается «меньше». На рис. 1.1 изображена ситуация, возникающая при 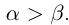 .
.
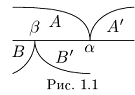
Из свойств числовых множеств очевидно следует, что:
1) 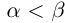 тогда и только тогда, когда
тогда и только тогда, когда 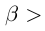
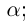 ;
;
2) если 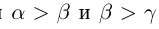 , то
, то 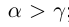 ; если
; если 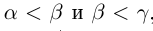 , то
, то  (транзитивность отношений неравенства).
(транзитивность отношений неравенства).
Теорема 1.1. Если действительные числа 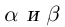 не равны (применяется обозначение
не равны (применяется обозначение 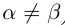 ), то либо
), то либо 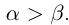 , либо
, либо 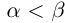 .
.
□ Пусть А и В — нижние классы сечений 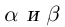 соответственно; тогда
соответственно; тогда 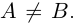 . Нужно доказать, что либо
. Нужно доказать, что либо 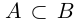 , либо
, либо 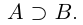
Но если включение 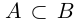 не выполнено, то существует рациональное число г1 такое, что
не выполнено, то существует рациональное число г1 такое, что 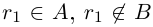 . Если включение
. Если включение 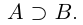 не выполнено, то существует рациональное число г2 такое, что
не выполнено, то существует рациональное число г2 такое, что 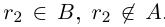 . Но тогда
. Но тогда 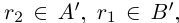 , т.е.
, т.е. 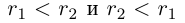 одновременно. Полученное противоречие показывает, что либо
одновременно. Полученное противоречие показывает, что либо 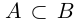 , либо
, либо 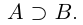 .
.
Доказанная теорема выражает свойство упорядоченности множества действительных чисел (если два числа не равны, то одно из них больше другого).
Теорема 1.2 (плотность рациональных чисел во множестве действительных чисел). Для любых действительных чисел 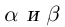 таких, что
таких, что 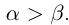 , найдётся рациональное число г такое, что
, найдётся рациональное число г такое, что 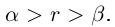 .
.
□ Так как 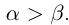 , то для соответствующих нижних классов
, то для соответствующих нижних классов 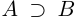 (строгое включение). Значит, найдётся рациональное число г такое, что
(строгое включение). Значит, найдётся рациональное число г такое, что 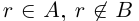 (см. рис. 1.2). Так как в нижнем классе нет наибольшего элемента, то
(см. рис. 1.2). Так как в нижнем классе нет наибольшего элемента, то 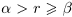 . Если
. Если 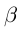 — иррациональное число, то
— иррациональное число, то 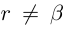 и
и 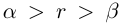 всё доказано. Если
всё доказано. Если 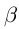 — рациональное число, то
— рациональное число, то 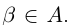 . Так как в А нет наибольшего элемента, то в качестве г можно рассмотреть число из А, которое больше
. Так как в А нет наибольшего элемента, то в качестве г можно рассмотреть число из А, которое больше 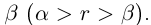 .
.
3амечание. Таких рациональных чисел г между 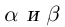 можно вставить бесконечно много (сначала
можно вставить бесконечно много (сначала 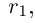 затем
затем 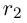 между
между 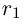 и а и т.д.).
и а и т.д.).
Теорема 1.3 (принцип Архимеда). Для любого действительного числа а существует натуральное число n, большее а.
□ Пусть 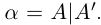 . Любое рациональное число
. Любое рациональное число 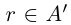 (кроме самого a, если
(кроме самого a, если 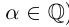 ) таково, что
) таково, что 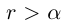 . Выберем натуральное
. Выберем натуральное 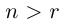 , тогда
, тогда 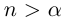 .
.
Следующее утверждение мы назовём леммой. Принципиального различия между теоремами и леммами нет, и то, и другое — утверждения, доказываемые в настоящем курсе. Теоремами обычно называют более фундаментальные утверждения, обладающие достаточной общностью формулировки, часто используемые в дальнейшем. Леммы обычно имеют более специальные формулировки и не так широко применяются в последующем изложении.
Лемма 1.1. Пусть 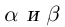 —действительные числа. Если для любого положительного рационального числа s найдутся рациональные числа
—действительные числа. Если для любого положительного рационального числа s найдутся рациональные числа 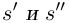 такие, что
такие, что 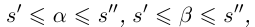
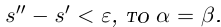
(Иными словами, если два действительных числа можно зажать между двумя сколь угодно близкими рациональными числами, то они равны.)
Как и в школьной программе, знак 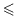 означает что либо числа равны, либо первое меньше второго (аналогично применяется знак
означает что либо числа равны, либо первое меньше второго (аналогично применяется знак 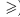 )
)
□Пусть 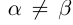 , для определённости
, для определённости 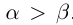 . По теореме 1.2 найдутся рациональные числа
. По теореме 1.2 найдутся рациональные числа 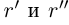 такие, что
такие, что 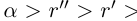
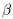 . Рассмотрим положительное рациональное число
. Рассмотрим положительное рациональное число 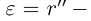
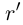 и соответствующие ему по условию рациональные числа
и соответствующие ему по условию рациональные числа 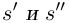 . Так как
. Так как 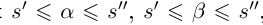 то
то 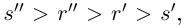 откуда
откуда 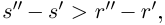 что противоречит тому, что
что противоречит тому, что 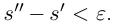
3амeчание. При формулировке подобных утверждений рекомендуется применять сокращённые записи, содержащие кванторы  (для любого, для всех, для каждого) и
(для любого, для всех, для каждого) и 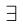 (существует, найдётся). Например, теорема 1.2 может быть сформулирована так:
(существует, найдётся). Например, теорема 1.2 может быть сформулирована так:
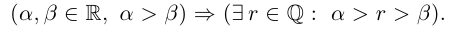
Лемма 1.1 может быть сформулирована так:
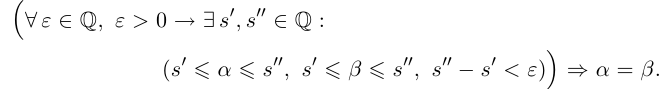
Такие записи являются лишь удобным сокращением словесных формулировок, и не следует считать, что в каждом конкретном случае данная запись является единственно возможной. Конечно, можно поставить вопрос о формальном языке, необходимом для таких записей, и довести их до логического совершенства. При этом придётся ввести символы  (или),
(или),  (и),
(и),  (пусть) и т.д.; придётся также договориться об аккуратности использования знаков : ;
(пусть) и т.д.; придётся также договориться об аккуратности использования знаков : ;  скобок и т.д. Ещё раз подчёркиваем, что такая постановка вопроса не является существенной для курса математического анализа. Без сокращённых логических записей можно обойтись, они просто очень удобны для восприятия и позволяют экономить бумагу и время.
скобок и т.д. Ещё раз подчёркиваем, что такая постановка вопроса не является существенной для курса математического анализа. Без сокращённых логических записей можно обойтись, они просто очень удобны для восприятия и позволяют экономить бумагу и время.
Во множестве действительных чисел можно строить сечения так же, как и во множестве рациональных чисел.
Определение 1.6. Сечением множества действительных чисел R называется такое разбиение R на два непустых множества 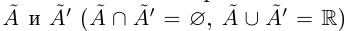 , что для всех
, что для всех 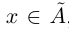
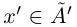 выполняется неравенство
выполняется неравенство 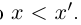 .
.
Одновременное существование наибольшего элемента в нижнем классе 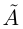 и наименьшего элемента в верхнем классе
и наименьшего элемента в верхнем классе 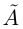 невозможно; доказательство аналогично соответствующему утверждению для сечений во множестве рациональных чисел. Оказывается, во множестве действительных чисел не может быть и сечений III типа. Имеет место
невозможно; доказательство аналогично соответствующему утверждению для сечений во множестве рациональных чисел. Оказывается, во множестве действительных чисел не может быть и сечений III типа. Имеет место
Теорема 1.4 (Дедекинда). Для любого сечения 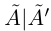 во множество R существует действительное число
во множество R существует действительное число 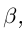 которое является либо наибольшим элементом в
которое является либо наибольшим элементом в 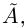 . либо наименьшим в
. либо наименьшим в 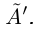
□ Пусть А — множество всех рациональных чисел из 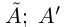
—множество всех рациональных чисел из 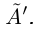 . Очевидно,
. Очевидно, 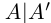
—сечение в Q, которое определяет некоторое действительное число 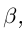 . Либо
. Либо 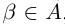 , либо
, либо 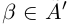 . Пусть для определённости
. Пусть для определённости 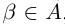 покажем, что
покажем, что 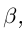 — наибольший элемент в
— наибольший элемент в 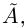 (аналогично, если
(аналогично, если 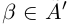 , доказывается, что
, доказывается, что 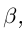 — наименьший элемент в А').
— наименьший элемент в А').
Предположим, что 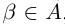 , но
, но 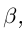 не является наибольшим в
не является наибольшим в 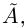 т.е. существует действительное число
т.е. существует действительное число 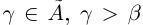 . По теореме 1.2 существует рациональное число г такое, что
. По теореме 1.2 существует рациональное число г такое, что 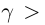
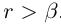 . Очевидно,
. Очевидно, 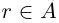 ; значит,
; значит, 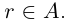 . Итак, г принадлежит нижнему классу сечения в Q, определяемому числом
. Итак, г принадлежит нижнему классу сечения в Q, определяемому числом 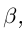 но в то же время
но в то же время 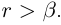 Полученное противоречие показывает, что
Полученное противоречие показывает, что 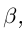 — наибольший элемент в
— наибольший элемент в 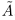 . ■
. ■
Заметим, что здесь не игнорируются сечения такие, что в нижнем классе есть наибольший элемент. В своё время это нужно было для установления взаимно однозначного соответствия между сечениями в Q и множеством R, здесь похожей необходимости нет.
Теорема Дедекинда отражает свойство полноты или непрерывности множества действительных чисел. Иррациональные числа, как сечения III типа, фактически являлись «дырками» во множестве рациональных чисел. Введение действительных чисел заполнило эти дырки. Теорема Дедекинда показывает, что во множестве действительных чисел таких дырок нет.
Свойство непрерывности показывает существенное отличие множества R от множества Q. Рассмотренные ранее свойства — упорядоченность, плотность, принцип Архимеда — имели место и во множестве Q.
Ограниченные множества. Точные верхние и нижние грани
Определение 1.7. Множество X, состоящее из действительных чисел, называется ограниченным сверху, если найдётся действительное число М такое, что для всех элементов х множества X выполняется неравенство 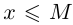 . Множество X, состоящее из действительных чисел, называется ограниченным снизу, если найдётся действительное число m такое, что для всех элементов х множества X выполняется неравенство
. Множество X, состоящее из действительных чисел, называется ограниченным снизу, если найдётся действительное число m такое, что для всех элементов х множества X выполняется неравенство  . Число М в этих определениях называется верхней границей множества X, число m — нижней границей. Множество X называется ограниченным, если оно ограничено и сверху и снизу.
. Число М в этих определениях называется верхней границей множества X, число m — нижней границей. Множество X называется ограниченным, если оно ограничено и сверху и снизу.
На языке кванторов ограниченность множества X сверху описывается следующей сокращённой записью:
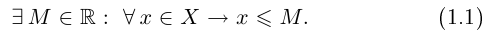
Ограниченность снизу описывается так:
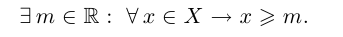
Пример 1.1. Пусть 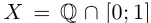 , т.е. X — множество рациональных точек отрезка [0; 1]. Это множество ограничено, так как для всех
, т.е. X — множество рациональных точек отрезка [0; 1]. Это множество ограничено, так как для всех 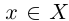 выполняются неравенства
выполняются неравенства 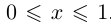 . Верхняя граница 1, нижняя граница 0. В то же время верхней границей может быть, например, число 2, нижней — число — 1.
. Верхняя граница 1, нижняя граница 0. В то же время верхней границей может быть, например, число 2, нижней — число — 1.
Таким образом, верхняя и нижняя границы множества определены неоднозначно.
Попытаемся сформулировать высказывание «Множество X, состоящее из действительных чисел, не является ограниченным сверху», не применяя частиц и приставок типа «не» и «нет», т.е. в позитивном смысле. Что означает невыполнение (1.1)? Это значит, что для любого действительного числа М не выполняется высказывание 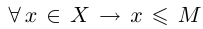 . Иными словами, для любого действительного числа М найдётся элемент
. Иными словами, для любого действительного числа М найдётся элемент 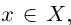 для которого выполняется противоположное неравенство х > М.
для которого выполняется противоположное неравенство х > М.
Запишем окончательно на языке кванторов, что означает неограниченность множества X сверху:
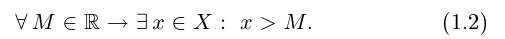
Наблюдая преобразование (1.1) в (1.2), мы можем сформулировать формальное правило построения отрицаний в позитивном смысле:
1) кванторы меняются друг на друга, т.е. 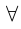 превращается в
превращается в 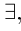
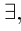 превращается в
превращается в 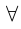 ;
;
2)высказывания, стоящие при кванторах, не меняются;
3)существенные высказывания, не стоящие при кванторах, меняются на противоположные.
Пример 1.2. Множество N натуральных чисел ограничено снизу 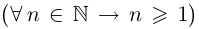 , но не является ограниченным сверху
, но не является ограниченным сверху 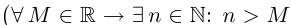 — принцип Архимеда).
— принцип Архимеда).
Определение 1.8. Действительное число л называется точной верхней гранью множества 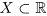 , если это число является верхней границей множества X, а никакое меньшее число не является верхней границей X.
, если это число является верхней границей множества X, а никакое меньшее число не является верхней границей X.
На языке кванторов это описывается как конъюнкция (т.е. одновременное выполнение) двух высказываний:
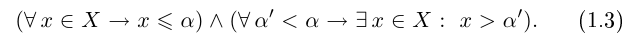
Логический символ 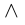 («и») означает одновременное выполнение двух высказываний.
(«и») означает одновременное выполнение двух высказываний.
Точная верхняя грань обозначается sup («supremum»):
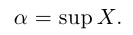
Определение 1.9. Действительное число 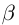 называется точной нижней гранью множества
называется точной нижней гранью множества 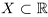 , если это число является нижней границей множества X, а никакое большее число не является нижней границей X.
, если это число является нижней границей множества X, а никакое большее число не является нижней границей X.
На языке кванторов записывается конъюнкция двух высказываний:
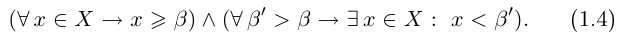
Точная нижняя грань обозначается inf («infimum»):
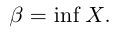
Из определений следует, что sup X — это наименьшая из верхних границ множества X, a inf X — это наибольшая из нижних границ. Пока ниоткуда не следует, что эти наименьшая из верхних и наибольшая из нижних границ существуют. Дело в том, что ограниченное сверху множество может иметь наибольший элемент, а может и не иметь; ограниченное снизу множество может иметь наименьший элемент, а может и не иметь.
Лемма 1.2. Если множество 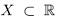 имеет наибольший элемент а, то а = sup X. Если множество
имеет наибольший элемент а, то а = sup X. Если множество 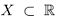 имеет наименьший элемент
имеет наименьший элемент 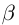 , то
, то 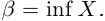
□ Доказательство приведём для наибольшего элемента, вторая часть доказывается аналогично.
Так как а — наибольший элемент X, то для всех 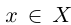 выполнено неравенство
выполнено неравенство 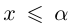 . С другой стороны, какое бы число
. С другой стороны, какое бы число 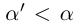 мы ни взяли, число л является элементом множества, и
мы ни взяли, число л является элементом множества, и 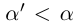 ; значит, для любого
; значит, для любого 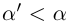 найдётся элемент X, больший а'. Доказано, что а = supX. ■
найдётся элемент X, больший а'. Доказано, что а = supX. ■
Но может быть и так, что во множестве нет наибольшего (наименьшего) элемента, а точная верхняя (нижняя) грань существует. В этом случае говорят, что точная верхняя (нижняя) грань не достигается.
Пример 1.3. Пусть 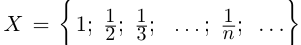 —множество всех чисел вида
—множество всех чисел вида 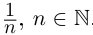 . Очевидно, наибольшим элементом множества является число 1; по лемме 1.2 supX = 1 (точная верхняя грань множества достигается).
. Очевидно, наибольшим элементом множества является число 1; по лемме 1.2 supX = 1 (точная верхняя грань множества достигается).
С другой стороны, ясно, что при всех 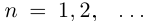 выполняется неравенство
выполняется неравенство 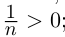 ; множество ограничено снизу, но наименьшего элемента в нём нет. Докажем, что inf X = 0 (таким образом, точная нижняя грань не достигается).
; множество ограничено снизу, но наименьшего элемента в нём нет. Докажем, что inf X = 0 (таким образом, точная нижняя грань не достигается).
□ В самом деле, для всех 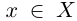 выполняется неравенство
выполняется неравенство 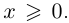 Но какое бы число
Но какое бы число 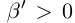 мы ни взяли, найдутся рациональное число г такое, что
мы ни взяли, найдутся рациональное число г такое, что 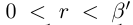 (теорема 1.2), и натуральное число п такое, что
(теорема 1.2), и натуральное число п такое, что 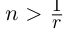 т.е.
т.е. 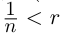 (свойства неравенств между рациональными числами мы считаем известными). Поэтому
(свойства неравенств между рациональными числами мы считаем известными). Поэтому 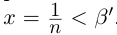 . Итак, для любого
. Итак, для любого 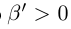 найдётся число
найдётся число 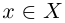 такое, что
такое, что 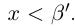 . Доказано, что inf X = 0. ■
. Доказано, что inf X = 0. ■
Теорема 1.5 (о точной верхней (нижней) грани). Для любого непустого множества действительных чисел, ограниченного сверху, существует и единственна точная верхняя грань. Для любого непустого множества действительных чисел, ограниченного снизу, существует и единственна точная нижняя грань.
□ Доказательство проведём для точной верхней грани, вторая часть доказывается аналогично (отметим, что пустое множество формально является ограниченным сверху и снизу, но говорить о точных верхней и нижней гранях бессмысленно).
Пусть сначала ограниченное сверху множество 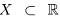 имеет наибольший элемент. Тогда по лемме 1.2 этот элемент является точной верхней гранью.
имеет наибольший элемент. Тогда по лемме 1.2 этот элемент является точной верхней гранью.
Пусть теперь в X нет наибольшего элемента. Проведём сечение во множестве К так, что А' — это все верхние границы X (они существуют в силу ограниченности X сверху), а 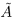 — все остальные числа. Ясно, что
— все остальные числа. Ясно, что 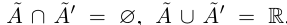 , для любых
, для любых 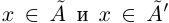 выполняется неравенство
выполняется неравенство 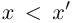 (ясно, что
(ясно, что 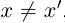 , но если
, но если 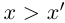 , то число х больше некоторой верхней границы, значит, х — тоже верхняя граница, а это не так). При этом
, то число х больше некоторой верхней границы, значит, х — тоже верхняя граница, а это не так). При этом 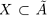 (если какой-то элемент X является верхней границей, то он наибольший в X, а мы рассматриваем случай, когда наибольшего элемента нет).
(если какой-то элемент X является верхней границей, то он наибольший в X, а мы рассматриваем случай, когда наибольшего элемента нет).
По теореме Дедекинда существует действительное число a либо наибольшее в 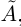 , либо наименьшее в
, либо наименьшее в 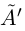 . Но если a — наибольшее число в
. Но если a — наибольшее число в 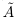 , то, так как
, то, так как 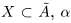 — верхняя граница для X, т.е.
— верхняя граница для X, т.е. 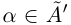 — противоречие. Значит, a — наименьшее число в
— противоречие. Значит, a — наименьшее число в 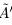 (наименьшая из верхних границ). Итак, а — верхняя граница X, а никакое меньшее число верхней границей не является, т.е. a = supX.
(наименьшая из верхних границ). Итак, а — верхняя граница X, а никакое меньшее число верхней границей не является, т.е. a = supX.
Докажем теперь, что точная верхняя грань единственна. Пусть a = supX и 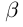 = supX. a <
= supX. a < 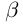 (для определённости). Тогда, так как
(для определённости). Тогда, так как 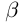 = sup X и a <
= sup X и a < 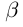 , то существует элемент
, то существует элемент 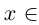 X, больший а. Это противоречит тому, что а = supX. ■
X, больший а. Это противоречит тому, что а = supX. ■
Отмстим ещё раз, что sup X — это наименьшая из верхних границ множества X, a inf X — это наибольшая из нижних границ X (теорема 1.5 утверждает, что во множестве верхних границ, существует наименьший элемент, а во множестве нижних границ существует наибольший элемент). Отсюда следует также
Лемма 1.3. Если число М является верхней границей множества X, то и sup 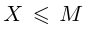 . Если число m является нижней границей множества X, то и inf
. Если число m является нижней границей множества X, то и inf 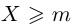 .
.
Запишем формулировку этой леммы на языке кванторов:
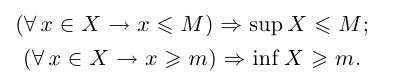
Отметим, кстати, что
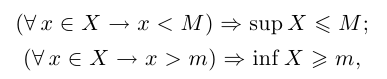
т.е. при переходе к точной верхней (нижней) грани строгое неравенство может превратиться в нестрогое. В примере 1.3 для всех  выполнено неравенство х > 0, a inf X = 0.
выполнено неравенство х > 0, a inf X = 0.
Определение 1.10. Если множество  неограничено сверху, то по определению supX =
неограничено сверху, то по определению supX = 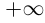 . Если множество
. Если множество 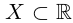 неограничено снизу, то по определению inf X =
неограничено снизу, то по определению inf X = 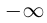 .
.
Представление действительных чисел бесконечными десятичными дробями
Пусть действительное число а не является целым числом или конечной десятичной дробью. Рассмотрим соответствующее сечение во множестве рациональных чисел 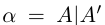 (в нижнем классе А нет наибольшего элемента).
(в нижнем классе А нет наибольшего элемента).
Обозначим через со наибольшее целое число в А. Тогда 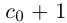 — наименьшее целое число в А'. Так как а не целое, то
— наименьшее целое число в А'. Так как а не целое, то 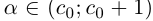 . Разобьём отрезок
. Разобьём отрезок 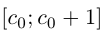 на 10 отрезков равной длины
на 10 отрезков равной длины 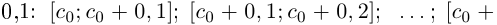
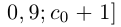 и выберем из них тот, который содержит число
и выберем из них тот, который содержит число
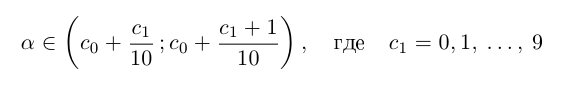
(a не совпадает с концом отрезка, так как не является конечной десятичной дробью).
Снова разбиваем полученный отрезок на 10 отрезков равной длины 0,01 и т.д., на n-м шагу получим
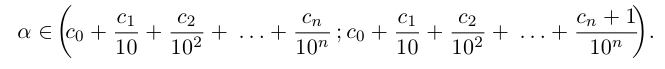
Здесь 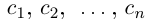 — «цифры», т.е. целые числа, принимающие значения 0,1, ..., 9. Длина отрезка на n-м шаге равна
— «цифры», т.е. целые числа, принимающие значения 0,1, ..., 9. Длина отрезка на n-м шаге равна 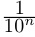 , а концы символически записываются в виде конечных десятичных дробей:
, а концы символически записываются в виде конечных десятичных дробей:
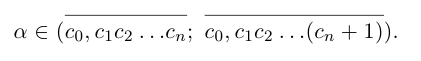
Естественно, что если сn = 9, то при переходе к правому концу отрезка предыдущую цифру 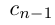 нужно увеличить на 1, а вместо сn + 1 написать 0. Если
нужно увеличить на 1, а вместо сn + 1 написать 0. Если  , то при переходе к правому концу отрезка
, то при переходе к правому концу отрезка 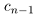 нужно увеличить на 1, и вместо
нужно увеличить на 1, и вместо 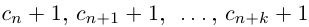 написать нули.
написать нули.
Так как а не является конечной десятичной дробью, то процесс никогда не оборвётся, и мы получим бесконечную последовательность цифр 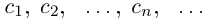 Бесконечную десятичную дробь
Бесконечную десятичную дробь 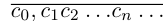 можно считать представлением действительного числа а.
можно считать представлением действительного числа а.
Например, для числа 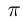 :
:
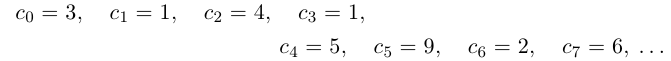
Описанная выше конструкция даст следующие интервалы:

Левый конец соответствующего интервала длины 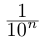 обычно называют десятичным приближением n-го порядка числа a с недостатком, правый конец — десятичным приближением n-го порядка числа а с избытком; применяются обозначения соответственно
обычно называют десятичным приближением n-го порядка числа a с недостатком, правый конец — десятичным приближением n-го порядка числа а с избытком; применяются обозначения соответственно 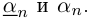 . Например:
. Например:
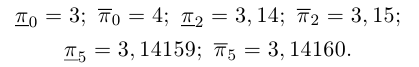
Бесконечная десятичная дробь 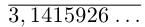 является представлением числа
является представлением числа 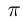 .
.
Интересно отмстить, что в такой конструкции для числа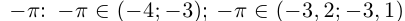 и т.д. Поэтому =
и т.д. Поэтому = 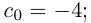
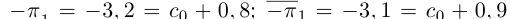 и т.д.;
и т.д.; 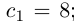
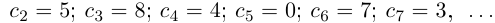
Представлением числа 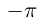 является бесконечная десятичная дробь
является бесконечная десятичная дробь 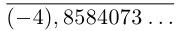
Легко видеть, что для любого 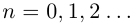
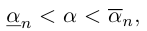 причем
причем 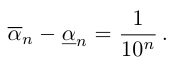
Особое значение имеет случай, когда а — конечная десятичная дробь с n знаками после запятой:
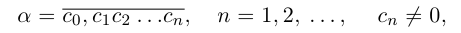
или целое число: 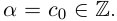
Случай целого a можно рассматривать как частный случай конечной десятичной дроби при n = 0.
В описанной выше конструкции после n-го шага процесс оборвётся. Число ft будет являться общим концом двух отрезков длины 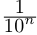 Если a рассматривается как левый коней, правого из двух возникших отрезков, то получим уже привычную десятичную дробь:
Если a рассматривается как левый коней, правого из двух возникших отрезков, то получим уже привычную десятичную дробь:
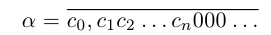
(для иллюстрации общности процесса мы дополнили её бесконечной последовательностью нулей). Если же a рассматривать как правый конец левого из двух возникших отрезков, то а представляется как бесконечная дробь, в которой начиная с (n + 1)-го места после запятой идут девятки:
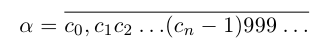
Таким образом, конечная десятичная дробь имеет два десятичных представления (с нулями, начиная с некоторого места, и с девятками, начиная с некоторого места). Например:
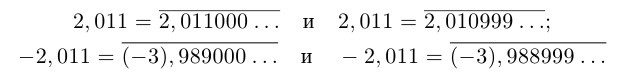
В любом случае при 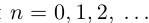
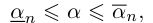 причём
причём 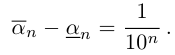
Докажем теперь очень важную лемму, которая неоднократно будет использоваться в дальнейшем в теории действительных чисел.
Лемма 1.4. Пусть a —действительное число. Тогда для любого рационального положительного числа s найдутся paциональные числа 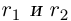 такие, что
такие, что 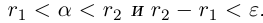
Иными словами, любое действительное число может быть зажато между двумя сколь угодно близкими рациональными числами.
□ Если a — рациональное число, то возьмём 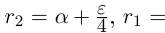
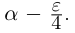 Ясно, что
Ясно, что 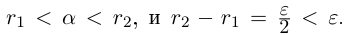 Если а — иррациональное число, то, во всяком случае, л не является конечной десятичной дробью, и
Если а — иррациональное число, то, во всяком случае, л не является конечной десятичной дробью, и 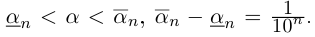
Поэтому можно взять 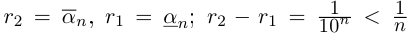 (неравенство
(неравенство 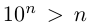 при любом натуральном n легко доказывается, например, по индукции). По принципу Архимеда для любого положительного рационального числа
при любом натуральном n легко доказывается, например, по индукции). По принципу Архимеда для любого положительного рационального числа 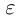 найдётся натуральное число
найдётся натуральное число 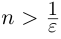 значит,
значит, 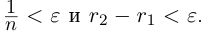
Мы видели, что любое действительное число представляется бесконечной десятичной дробью. Это представление единственно, если действительное число не является целым или конечной десятичной дробью, в противном случае таких представлений два. Докажем обратное утверждение.
Теорема 1.6. Любая бесконечная десятичная дробь является представлением некоторого действительного числа, причем это число определяется единственным образом.
□ Пусть 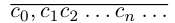 — бесконечная десятичная дробь
— бесконечная десятичная дробь  . Рассмотрим при
. Рассмотрим при 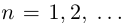 , рациональные числа
, рациональные числа 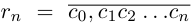 и
и 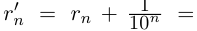
 — приближения для данной дроби с недостатком и с избытком соответственно. Ясно, что для всех
— приближения для данной дроби с недостатком и с избытком соответственно. Ясно, что для всех 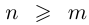 выполняется неравенство
выполняется неравенство 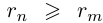 , поэтому
, поэтому 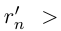
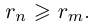
Пусть теперь 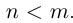 Тогда
Тогда
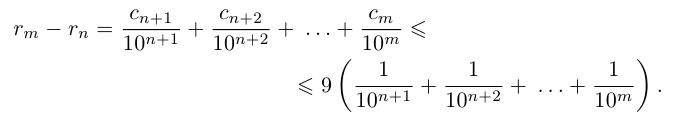
Применяя формулу суммы членов геометрической прогрессии, получим
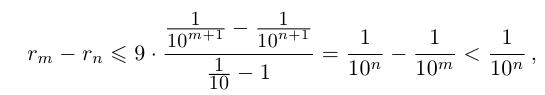
поэтому 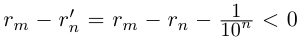 . Итак, при любых натуральных значениях m и n выполняется неравенство
. Итак, при любых натуральных значениях m и n выполняется неравенство 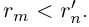 .
.
Рассмотрим множества рациональных чисел
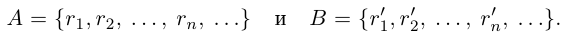
При фиксированном 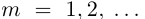 выполняется неравенство
выполняется неравенство 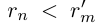 для любого натурального n, поэтому множество А ограничено сверху, и по лемме 1.3 его точная верхняя грань
для любого натурального n, поэтому множество А ограничено сверху, и по лемме 1.3 его точная верхняя грань
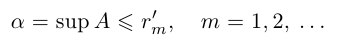
Аналогично, при фиксированном 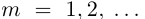 выполняется неравенство
выполняется неравенство 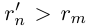 для любого натурального n, поэтому множество В ограничено снизу, и по лемме 1.3 его точная нижняя грань
для любого натурального n, поэтому множество В ограничено снизу, и по лемме 1.3 его точная нижняя грань
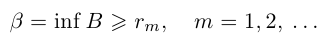
Из леммы 1.3 и последнего неравенства, верного при всех 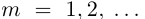 , следует, что
, следует, что 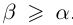 . Итак, при всех
. Итак, при всех 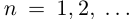 имеют место неравенства
имеют место неравенства 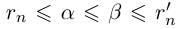 и
и 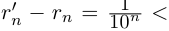
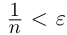 при
при 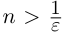 (
(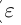 — произвольное положительное рациональное число). По лемме 1.1 а =
— произвольное положительное рациональное число). По лемме 1.1 а = 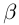 . Так как
. Так как 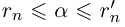 при
при 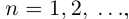 , то данная бесконечная десятичная дробь является представлением числа а.
, то данная бесконечная десятичная дробь является представлением числа а.
Единственность искомого действительного числа следует из леммы 1.1. В самом деле, если два числа 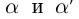 являются представлениями одной и той же бесконечной десятичной дроби, то из неравенств
являются представлениями одной и той же бесконечной десятичной дроби, то из неравенств 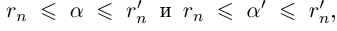
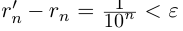 (где
(где 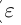 — произвольное положительное рациональное число) следует, что
— произвольное положительное рациональное число) следует, что 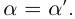
Арифметические операции с действительными числами
Нам предстоит определить для действительных чисел арифметические операции (сложение, вычитание, умножение, деление) так, чтобы сохранялись привычные свойства этих операций, а для рациональных чисел результаты операций не отличались от обычных.
Пусть 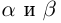 — два действительных числа. Будем рассматривать всевозможные рациональные числа
— два действительных числа. Будем рассматривать всевозможные рациональные числа 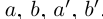 удовлетворяющие неравенствам
удовлетворяющие неравенствам
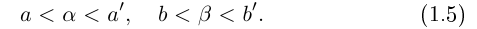
Определение 1.11. Суммой 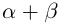 действительных чисел
действительных чисел 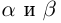 называется действительное число
называется действительное число 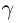 такое, что для любых рациональных чисел
такое, что для любых рациональных чисел 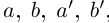 удовлетворяющих неравенствам (1.5), выполняется неравенство
удовлетворяющих неравенствам (1.5), выполняется неравенство
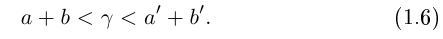
Докажем корректность этого определения. Иными словами, докажем, что такое действительное число 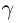 существует, определено единственным образом, а в случае рациональных
существует, определено единственным образом, а в случае рациональных 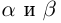 построенное таким образом число
построенное таким образом число 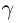 совпадает с суммой рациональных чисел
совпадает с суммой рациональных чисел 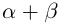 .
.
□ I) Существование. Рассмотрим множество всевозможных сумм {а + b} в условиях (1.5). Оно ограничено сверху некоторой суммой 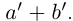 Рассмотрим число
Рассмотрим число 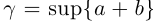 в условиях (1.5).
в условиях (1.5).
Тогда при выполнении условий (1.5) 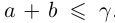 . Но так как при фиксированных
. Но так как при фиксированных 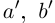 в условиях (1.5) выполняется неравенство
в условиях (1.5) выполняется неравенство 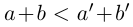 для любых a, b в условиях (1.5), то по лемме 1.3,
для любых a, b в условиях (1.5), то по лемме 1.3, 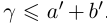 . Итак, в условиях (1.5)
. Итак, в условиях (1.5) 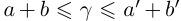 . Исключим равенства. Пусть найдутся a, b такие, что
. Исключим равенства. Пусть найдутся a, b такие, что 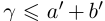 . Но по теореме 1.2 найдутся рациональные числа
. Но по теореме 1.2 найдутся рациональные числа 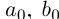 такие, что
такие, что 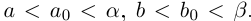 . Значит,
. Значит, 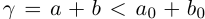 , что противоречит определению
, что противоречит определению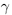 как sup{a + b} в условиях (1.5). Значит,
как sup{a + b} в условиях (1.5). Значит, 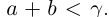 . Аналогично показывается, что
. Аналогично показывается, что 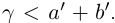 Построенное число
Построенное число 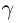 удовлетворяет условиям (1.6).
удовлетворяет условиям (1.6).
II) Единственность. По лемме 1.4 для любого положительного рационального числа 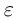 найдутся рациональные числа
найдутся рациональные числа 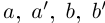 в условиях (1.5) такие, что
в условиях (1.5) такие, что 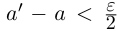
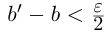 . Тогда
. Тогда
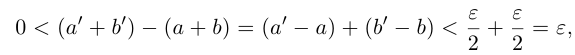
и эта разность может быть сделана сколь угодно малой. По лемме 1.1 существует единственное действительное число 7, удовлетворяющее условиям (1.6).
III) Преемственность. Если 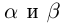 — оба рациональные числа, то их обычная рациональная сумма
— оба рациональные числа, то их обычная рациональная сумма 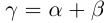 удовлетворяет определению 1.11, и в силу единственности другой суммы быть не может. ■
удовлетворяет определению 1.11, и в силу единственности другой суммы быть не может. ■
Теперь нужно показать, что привычные свойства операции сложения сохраняются для определённого таким образом сложения действительных чисел. Ввиду большого количества этих свойств будут проведены доказательства лишь некоторых из них; доказать остальные читатели смогут самостоятельно (наиболее существенные моменты будут показаны в доказательствах, приведённых здесь).
Свойства сложения действительных чисел
1)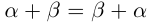 (коммутативность).
(коммутативность).
□ Рассмотрим рациональные числа 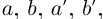 удовлетворяющие условиям (1.5). Тогда для чисел
удовлетворяющие условиям (1.5). Тогда для чисел 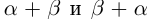 (пока мы не знаем, что они равны)
(пока мы не знаем, что они равны)
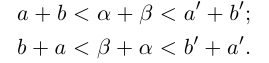
Так как сложение рациональных чисел коммутативно, то а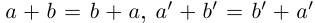 , поэтому действительные числа
, поэтому действительные числа 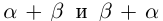 заключены в одних и тех же границах, разность между которыми может быть сделана сколь угодно малой (аналогично II в доказательстве корректности определения 1.11). По лемме 1.1
заключены в одних и тех же границах, разность между которыми может быть сделана сколь угодно малой (аналогично II в доказательстве корректности определения 1.11). По лемме 1.1 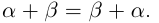
2)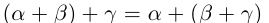 (ассоциативность).
(ассоциативность).
3)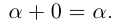
4)Для любого действительного числа а найдётся число 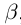 , называемое противоположным числом и обозначаемое
, называемое противоположным числом и обозначаемое 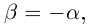 такое, что
такое, что 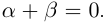
□ Если а — рациональное число, то 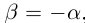 , где (-а) — соответствующее рациональное число. Пусть теперь
, где (-а) — соответствующее рациональное число. Пусть теперь 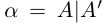 — иррациональное число. Рассмотрим число
— иррациональное число. Рассмотрим число  такое, что
такое, что 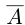 — множество всех элементов
— множество всех элементов 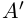 со знаком минус,
со знаком минус, 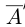 — множество всех элементов А со знаком минус. Очевидно, что это сечение, где в
— множество всех элементов А со знаком минус. Очевидно, что это сечение, где в 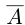 нет наибольшего, а в
нет наибольшего, а в 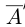 нет наименьшего элемента, т.е.
нет наименьшего элемента, т.е. 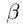 — иррациональное число. Рассмотрим всевозможные рациональные числа
— иррациональное число. Рассмотрим всевозможные рациональные числа 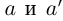 такие, что
такие, что 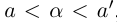 , тогда
, тогда 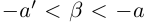 . По определению суммы действительных чисел число
. По определению суммы действительных чисел число 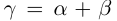 удовлетворяет неравенствам
удовлетворяет неравенствам 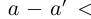
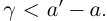 По лемме 1.4 разность а' — а может быть сделана меньше
По лемме 1.4 разность а' — а может быть сделана меньше 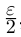 где
где 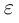 — произвольное положительное рациональное число. Тогда разность
— произвольное положительное рациональное число. Тогда разность 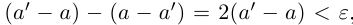 , и по лемме 1.1
, и по лемме 1.1 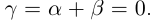 ■
■
Так как операция сложения во множестве действительных чисел удовлетворяет условиям 1) - 4), то на языке высшей алгебры «действительные числа образуют коммутативную группу по сложению». В такой группе противоположный элемент всегда определён единственным образом.
5)Если 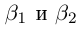 — два противоположных числа для действительного числа а, то
— два противоположных числа для действительного числа а, то 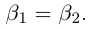
□ С одной стороны, 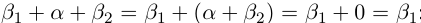 с другой стороны,
с другой стороны, 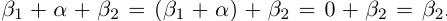 Значит,
Значит, 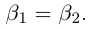 ■
■
6)Если 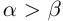 , то
, то  для любого
для любого 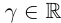
□ По лемме 1.2 найдутся рациональные числа 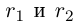 такие, что
такие, что 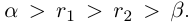 По лемме 1.4 найдутся рациональные числа с и с' такие, что
По лемме 1.4 найдутся рациональные числа с и с' такие, что 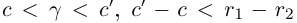 . Отсюда получим
. Отсюда получим
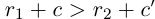 (свойство сложения рациональных чисел);
(свойство сложения рациональных чисел);
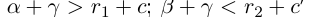 (определение суммы действительных чисел).
(определение суммы действительных чисел).
Значит,  ■
■
7)Если 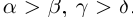 , то
, то 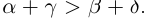
□ Двукратное применение предыдущего свойства. ■
8)Если 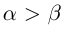 , то
, то 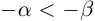
9)Если а > 0, то —а < 0.
Определение 1.12. Разностью 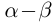 двух действительных чисел
двух действительных чисел 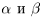 называется число
называется число 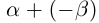 .
.
10)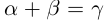 тогда и только тогда, когда
тогда и только тогда, когда 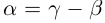 (перенос слагаемого в другую часть равенства с противоположным знаком).
(перенос слагаемого в другую часть равенства с противоположным знаком).
□ С одной стороны, 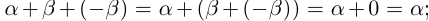 с другой стороны,
с другой стороны, 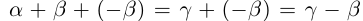 Значит,
Значит, 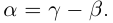
11)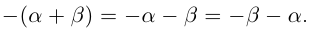
12)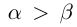 тогда и только тогда, когда
тогда и только тогда, когда 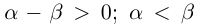 тогда и только тогда, когда
тогда и только тогда, когда 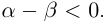
Определение 1.13. Модулем (абсолютной величиной) действительного числа а называется число, обозначаемое 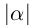 и равное а, если
и равное а, если 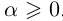 , и равное —а, если а < 0.
, и равное —а, если а < 0.
13)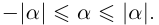
14)Если 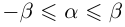 , где
, где 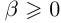 , то
, то 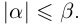
15)
□ Так как 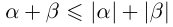 (свойства 13 и 7) и
(свойства 13 и 7) и 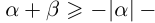
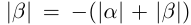 (свойства 13, 7 и 11), то по свойству 14
(свойства 13, 7 и 11), то по свойству 14 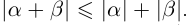
16)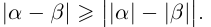
Определим теперь умножение действительных чисел.
Определение 1.14. I. Пусть  —два положительных действительных числа, т.е.
—два положительных действительных числа, т.е. 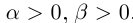 . Будем рассматривать всевозможные рациональные числа
. Будем рассматривать всевозможные рациональные числа 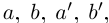 , удовлетворяющие неравенствам
, удовлетворяющие неравенствам
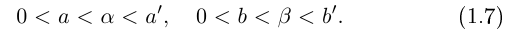
Произведением  чисел
чисел 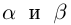 называется действительное число
называется действительное число 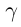 такое, что для любых рациональных чисел
такое, что для любых рациональных чисел 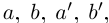 удовлетворяющих неравенствам (1.7), выполняется неравенство
удовлетворяющих неравенствам (1.7), выполняется неравенство

II.Для любого действительного числа а
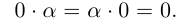
III.Если действительные числа 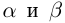 не равны нулю, то их произведением называется действительное число
не равны нулю, то их произведением называется действительное число 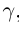 равное
равное 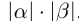 если
если 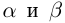 одного знака, и равное
одного знака, и равное 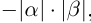 если
если 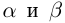 разных знаков.
разных знаков.
Корректность части I определения 1.14 доказывается аналогично корректности определения 1.11. При этом доказательства существования и преемственности сохраняются дословно с заменой там, где нужно, суммы на произведение. Доказательство единственности чуть сложнее.
□ Пусть n — некоторое натуральное число, большее чисел 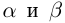 . Тогда по смыслу определения 1.14 можно считать, что рациональные числа
. Тогда по смыслу определения 1.14 можно считать, что рациональные числа 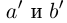 берутся меньшими, чем n. По лемме 1.4 для любого положительного рационального числа е найдутся рациональные числа
берутся меньшими, чем n. По лемме 1.4 для любого положительного рационального числа е найдутся рациональные числа 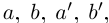 в условиях (1.7) такие, что
в условиях (1.7) такие, что 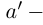
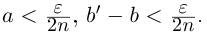 Тогда
Тогда
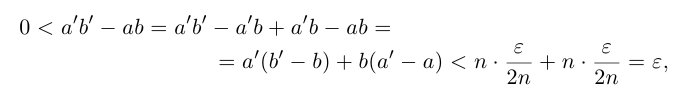
и эта разность может быть сделана сколь угодно малой (мы считаем, что 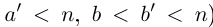 . По лемме 1.1 существует единственное действительное число
. По лемме 1.1 существует единственное действительное число  , удовлетворяющее условиям (1.8). ■
, удовлетворяющее условиям (1.8). ■
Свойства умножения действительных чисел аналогичны соответствующим свойствам сложения. Они здесь приводятся без доказательств, которые аналогичны доказательствам свойств сложения.
17)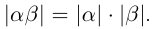
18)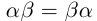 (коммутативность).
(коммутативность).
19)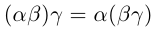 (ассоциативность).
(ассоциативность).
20)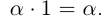
21)Для любого ненулевого действительного числа а найдётся число 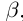 называемое обратным числом и обозначаемое
называемое обратным числом и обозначаемое 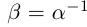 , такое, что
, такое, что 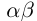 = 1.
= 1.
Свойства 18) - 21) означают на языке высшей алгебры, что «ненулевые действительные числа образуют коммутативную группу по умножению». Свойства 1) - 4) и 18) - 21) вместе означают что «действительные числа образуют поле относительно операций сложения и умножения».
22)Обратный элемент для любого ненулевого действительного числа определён единственным образом.
23)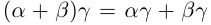 (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
□ Рассмотрим сначала случай, когда все числа 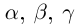 положительны. Пусть
положительны. Пусть  — всевозможные рациональные числа, удовлетворяющие условиям
— всевозможные рациональные числа, удовлетворяющие условиям
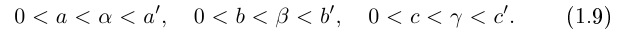
Если n — некоторое натуральное число, большее чисел 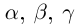 , то можно считать, что рациональные числа
, то можно считать, что рациональные числа 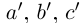 меньше, чем n. Для чисел
меньше, чем n. Для чисел 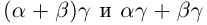 (пока мы не знаем, что они равны) выполняются неравенства
(пока мы не знаем, что они равны) выполняются неравенства
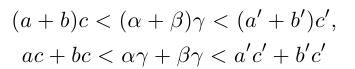
(по определению суммы и произведения положительных действительных чисел). В силу дистрибутивности умножения рациональных чисел относительно сложения 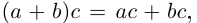
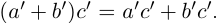 Поэтому действительные числа
Поэтому действительные числа 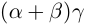 и
и 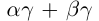 заключены в одних и тех же границах, разность между которыми может быть сделана сколь угодно малой.
заключены в одних и тех же границах, разность между которыми может быть сделана сколь угодно малой.
В самом деле, по лемме 1.4 найдутся рациональные числа 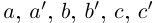 условиях (1.9) такие, что
условиях (1.9) такие, что
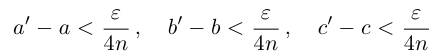
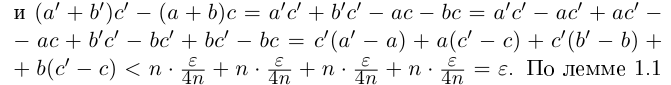
существует единственное такое действительное число, откуда
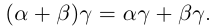
К случаю положительных 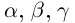 приводятся все остальные путём изменения знаков обеих частей равенства или переноса членов из одной части в другую. Если одно из чисел
приводятся все остальные путём изменения знаков обеих частей равенства или переноса членов из одной части в другую. Если одно из чисел 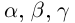 или
или 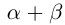 равно нулю, то искомое равенство очевидно. ■
равно нулю, то искомое равенство очевидно. ■
24)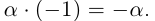
25)Если 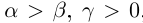 , то
, то 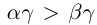 ; если
; если 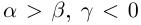 , то
, то 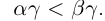
Определение 1.15. Частным 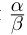 двух действительных чисел
двух действительных чисел 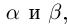 где
где 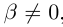 , называется число
, называется число 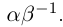
26)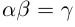 тогда и только тогда, когда
тогда и только тогда, когда 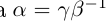 , т.е
, т.е 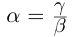 (здесь считается, что
(здесь считается, что 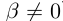 ).
).
27)Если 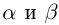 отличны от нуля, то
отличны от нуля, то 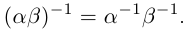
28)Если 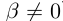 , то
, то 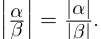
29)Если 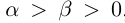 то
то 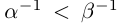 ; если
; если 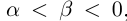 то
то 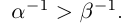
30)Если а — действительное число, a n — натуральное число, то число па равно сумме п слагаемых, равных а:
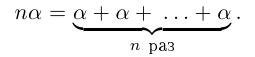
Вывод. Для действительных чисел имеют место все правила элементарной алгебры, относящиеся к четырём арифметическим действиям, равенствам и неравенствам.
Естественным образом определяется аn, где а — действительное, n — натуральное число:
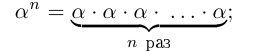
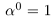 , если
, если 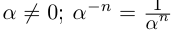 если
если 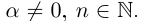
Сохраняются все свойства степеней с целым показателем (доказательства ничем не отличаются от доказательств в школьном курсе алгебры).
Обратим теперь внимание на то, что в лемме 1.1 действительное число зажималось между рациональными потому, что у нас ещё не было понятия разности действительных чисел. Приведём теперь более общий вариант этого утверждения.
Лемма 1.5. Пусть 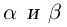 —действительные числа. Если для любого положительного действительного числа £ найдутся действительные числа
—действительные числа. Если для любого положительного действительного числа £ найдутся действительные числа 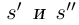 такие, что
такие, что 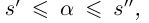
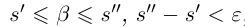 , то
, то 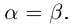
□ Пусть 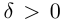 — произвольное рациональное число;
— произвольное рациональное число; 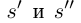 — такие действительные числа, что
— такие действительные числа, что 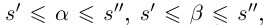
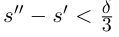 (они существуют по условию леммы при
(они существуют по условию леммы при 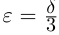 )
)
По лемме 1.4 найдутся рациональные числа 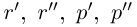 такие, что
такие, что
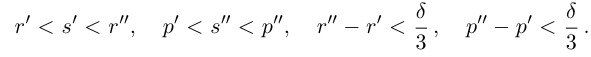
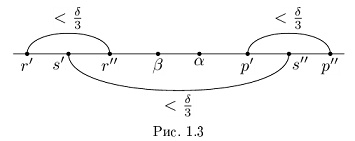
Тогда (см. рис. 1.3): 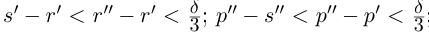
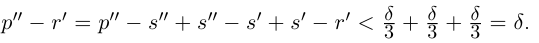
Итак, для любого рационального положительного числа 6 найдутся рациональные числа 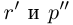 такие, что
такие, что
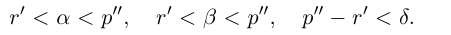
По лемме 1.1 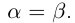
Счётные и несчётные множества
Определение 1.16. Два множества А и В называются эквивалентными (равномощными), если между А и В можно установить взаимно однозначное (биективное) соответствие.
Здесь мы фактически имеем дело с переводом русскоязычного термина на латинский язык (равномощный — эквивалентный, взаимно однозначное — биективное и т.д.). В принципе вполне можно было бы ограничиться русскоязычными терминами, но, поскольку их переводы очень распространены в отечественной научной и учебной литературе, их игнорировать нельзя.
Пример 1.4. Множество натуральных чисел эквивалентно множеству чётных натуральных чисел (взаимно однозначное соответствие устанавливается зависимостью 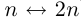 ), хотя одно из этих множеств является подмножеством другого.
), хотя одно из этих множеств является подмножеством другого.
Определение 1.17. Множество называется счётным, если оно эквивалентно множеству натуральных чисел (т.е. если его элементы можно занумеровать в виде бесконечной последовательности).
Лемма 1.6. Любое бесконечное множество содержит счётное подмножество.
□ Выберем некоторый элемент х1, принадлежащий данному бесконечному множеству А. Так как множество бесконечно, то можно выбрать элемент х2 среди оставшихся элементов, х3 среди оставшихся и т.д. Процесс не оборвётся в силу бесконечности А. Построенное счётное множество 
 (возможно, совпадает с A).
(возможно, совпадает с A).
Лемма 1.7. Любое бесконечное подмножество счётного множества счётно.
□ Пусть  — счётное множество, В — бесконечное. Докажем, что В — счётно. Пусть
— счётное множество, В — бесконечное. Докажем, что В — счётно. Пусть 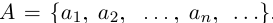 Выберем первый из этих элементов, принадлежащий В:
Выберем первый из этих элементов, принадлежащий В: 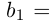
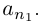 Из оставшихся номеров выберем первый
Из оставшихся номеров выберем первый 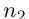 такой, что
такой, что 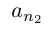 принадлежит В;
принадлежит В; 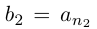 (ясно, что
(ясно, что 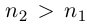 ). Из оставшихся номеров выберем первый
). Из оставшихся номеров выберем первый 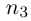 такой, что
такой, что 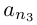 принадлежит
принадлежит 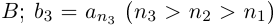 , и т.д. Каждый элемент В имеется среди
, и т.д. Каждый элемент В имеется среди 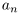 , поэтому через конечное число шагов он будет обозначен:
, поэтому через конечное число шагов он будет обозначен: 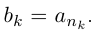 Таким образом, все элементы В занумерованы, и В — счётно.
Таким образом, все элементы В занумерованы, и В — счётно.
Лемма 1.8. Сумма конечного и счётного множеств, двух счётных множеств — счётна.
□ Напомним, что в теории множеств разностью множеств В \ А называется множество тех и только тех элементов, которые принадлежат В, но не принадлежат А (на диаграмме Эйлера заштрихована разность В \ А — см. рис. 1.4).
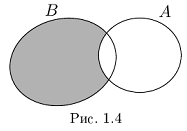
Из рис. 1.4 очевидны равенства
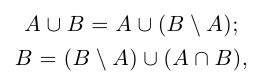
причём множества, объединяемые в правых частях этих равенств, имеют пустые пересечения.
1) Пусть А — счётно, В — конечно.
Если 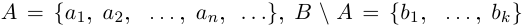 — также конечно (а может быть, и пусто), то
— также конечно (а может быть, и пусто), то 
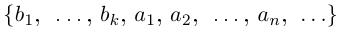 — счётное множество.
— счётное множество.
2) Пусть А и В счётны. Если В \ А конечно, то доказательство проходит, как в первом случае. Если В \ А бесконечно, т.е. счётно, то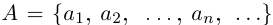 В \ А =
В \ А = 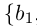
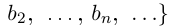 и
и 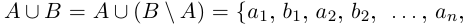
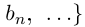 — счётное множество. ■
— счётное множество. ■
Теорема 1.7. Множество рациональных чисел Q счётно.
□ Достаточно доказать, что счётно множество положительных рациональных чисел Q+, так как в этом случае множество отрицательных рациональных чисел, эквивалентное ему 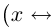
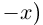 , также счётно, и вместе с единственным числом {0} по лемме 1.8 они все в сумме образуют счётное множество. Занумеруем Q+ следующим образом (см. рис. 1.5):
, также счётно, и вместе с единственным числом {0} по лемме 1.8 они все в сумме образуют счётное множество. Занумеруем Q+ следующим образом (см. рис. 1.5):
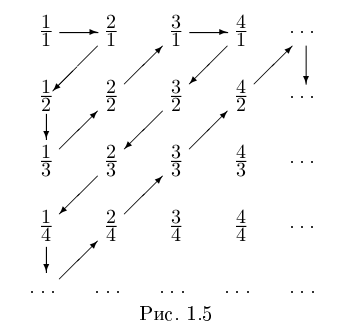
Занумерованы все положительные рациональные числа, причём каждое число встречается много раз  и т.д.). Таким образом, Q+ — бесконечное подмножество счётного множества. Значит, оно счётно. ■
и т.д.). Таким образом, Q+ — бесконечное подмножество счётного множества. Значит, оно счётно. ■
Следствие. Множество целых чисел Z счётно (принадлежит Q).
Теорема 1.8. Множество действительных чисел К несчётно (т.е. действительных чисел «значительно больше», чем рациональных).
□ Достаточно доказать, что несчётным является множество действительных чисел полуинтервала [0; 1) (если R — счётно, то [0; 1)  — также счётно). Предположим, удалось занумеровать все числа
— также счётно). Предположим, удалось занумеровать все числа 
Выпишем десятичные представления этих чисел:

при этом конечная десятичная дробь записывается с нулями, начиная с некоторого номера (а не с девятками).
Рассмотрим число  такое, что
такое, что 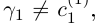
 (это число существует по теореме 1.6). Такого числа нет среди
(это число существует по теореме 1.6). Такого числа нет среди 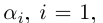
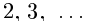 хотя
хотя 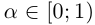 . Получили противоречие тому, что все числа [0; 1) удалось занумеровать. ■
. Получили противоречие тому, что все числа [0; 1) удалось занумеровать. ■
Следствие 1. Множество иррациональных чисел несчётно (иначе вместе с Q получилось бы счётное множество R).
Следствие 2. Множество чисел любого конечного интервала несчётно.
□ Множество (0; 1) несчётно, так как иначе при добавлении одной точки 0 получилось бы счётное множество [0; 1).
Несчётность произвольного интервала (а;b) следует из того, что между (0; 1) и (a: b) можно установить взаимно однозначное соответствие по формуле 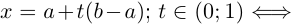
Замечание к главе I. При помощи сечений были определены лишь арифметические операции с действительными числами. Развивая этот метод, можно определить арифметический корень n-й степени из положительного действительного числа, степень положительного числа с произвольным действительным показателем, логарифмы и другие элементарные функции, известные из школьного курса алгебры. Но если этим вопросам уделить внимание в лекционном курсе математического анализа, то возникнет нехватка времени для изложения последующих очень существенных глав.
Представляется удобным и разумным пойти путём наименьшего сопротивления — не вводить пока эти элементарные функции, ограничившись в главах II и III (теория пределов последовательностей и функций) арифметическими свойствами действительных чисел. И только в главе III, после изучения свойств непрерывных функций, ввести корень n-й степени как обратную функцию к хn на соответствующем промежутке, аккуратно определить степень с действительным показателем, логарифм как обратную функцию и т.д. Этот путь имеет один недостаток — обедняется практическая сторона курса, при решении иллюстрирующих примеров приходится ограничиваться арифметическими операциями. Конечно, на практических занятиях следует решать примеры с корнями, логарифмами, тригонометрическими функциями и т.д., но при этом понимать, что всё, выходящее за рамки арифметики, пока является «незаконным» и чисто иллюстративным.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |