Давление в жидкостях и газах в физике - формулы и определение с примерами

Механическое движение жидкостей и газов, как и твердых тел, подчиняется законам механики Ньютона. При этом так же. как и в механике твердого тела, не изучают молекулярное строение жидкостей и газов, а рассматривают их как среду, в которой вещество распределено непрерывно. Раздел механики, изучающий равновесие жидкостей и газов, называется гидростатикой. Движение жидкостей изучается в гидродинамике, а газов — в аэродинамике. Следует заметить, что основные законы, которым подчиняются движение и равновесие жидкостей и газов, одинаковы. Поэтому под термином «жидкость» понимают и жидкость, и газ.

Давление в жидкостях и газах

Давайте вспомним и уточним некоторые понятия и законы статики жидкостей, известные из физики 7-го класса.

В отличие от твердых тел жидкости и газы не имеют определенной формы. Газы равномерно заполняют весь объем. Вследствие текучести жидкость принимает форму сосуда, в котором находится, занимая обычно часть объема сосуда. Объем жидкости сохраняется. Между жидкостью и остальной частью объема сосуда, наполненного парами жидкости и воздухом, образуется свободная поверхность. Когда сосуд неподвижен, свободная поверхность строго горизонтальна, т. е. вектор ускорения свободного падения ĝ перпендикулярен поверхности. Только у стенок сосуда поверхность жидкости несколько искривляется. Это явление будет объяснено впоследствии при изучении молекулярной физики.
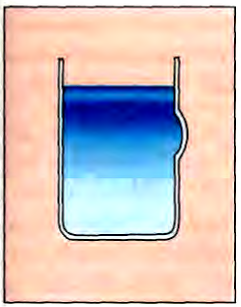
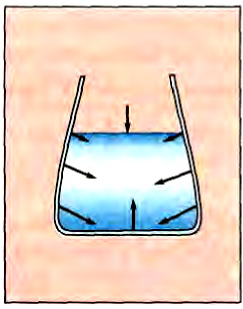
Налитая в сосуд жидкость вызывает деформацию стенок. Эту деформацию трудно заметить, если стенки твердые. Но если в сосуде сделать отверстие и заклеить его эластичной пленкой, то деформация стенки будет заметна (рис. 158). Таким образом, жидкость действует на стенки сосуда, а возникающие упругие силы в стенках действуют на жидкость по третьему закону Ньютона. Эти силы перпендикулярны поверхности стенки в каждой ее точке. На свободную поверхность жидкости тоже действуют перпендикулярные силы :о стороны воздуха (рис. 159). Таким образом, жидкость находится в сжатом состоянии. Это утверждение справедливо и для газов. Воздух атмосферы Земли сжимает сила тяготения.

Внутри жидкости возникают силы упругости, называемые силами давления. Для характеристики этих упругих напряжений вводят понятие давления.

Рассмотрим цилиндрический сосуд с жидкостью, закрытый поршнем (рис. 160). На поршень действует сверху сила 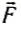и со стороны жидкости сила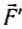. Поскольку поршень неподвижен, а силой тяжести поршня пока можно пренебречь, то поршень действует на жидкость с силой 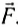. Причем эта сила равномерно распределена по поверхности жидкости. Отношение модуля силы 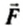к площади поверхности называется давлением:

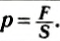
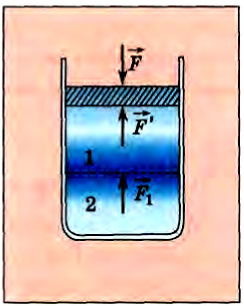
Рис. 160

В системе СИ давление измеряется в паскалях (1 Па =).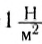
Мысленно проведем в жидкости горизонтальную плоскость, разделяющую ее на две части (см. рис. 160). Часть 1 находится в равновесии, следовательно, со стороны части 2 действует сила 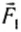, равномерно распределенная по площади. Значит, напряженное состояние жидкости в этой плоскости можно охарактеризовать давлением:

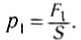
Поскольку плоскость мы провели произвольно, то, следовательно, напряженное состояние жидкости в каждой точке характеризуется давлением.

Выделим мысленно вертикальный столб жидкости высотой h, основанием которого является площадка площади S (рис. 161). Объем выделенного столба жидкости равен Sh и его масса m = pSh. На верхнее основание столба действует сила атмосферного давления F₀=p₀S, на нижнее основание — сила давления F₁=p₁S. Так как жидкость неподвижна, то сумма сил давления и силы тяжести столба жидкости должна быть равна нулю. В проекции на вертикальное направление можно записать:

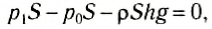
или

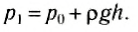
Итак, давление внутри жидкости на любой глубине h слагается из атмосферного давления (или внешнего давления) на жидкость и давления pgh, обусловленного действием силы тяжести, которое называется гидростатическим давлением.

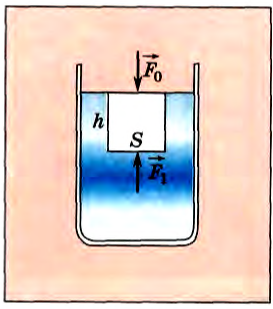
Рис. 161

В метрологии широко используется внесистемная единица давления 1 мм. рт. ст. Это давление, которое оказывает столбик ртути высотой 1 мм.

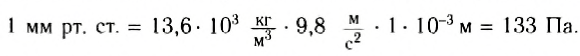
Из-за того что по мере погружения в жидкость давление возрастает, для постройки подводных лодок и батискафов используют особо прочные материалы. Увеличение давления с глубиной ощущают работающие под водой водолазы, спортсмены, увлекающиеся подводным плаванием.
Следует отметить, что формула (2) получена в предположении, что плотность жидкости не изменяется с глубиной, т. е. жидкость несжимаема.

Формулой (2) можно пользоваться и для расчета давления воздуха на некоторой высоте. Хотя газы значительно легче сжимаются, чем жидкости, для небольших высот сжимаемостью воздуха можно пренебречь. Например, значения давления атмосферного воздуха, рассчитанные по формуле (2) и по более точной формуле для высоты 1000 м над поверхностью Земли, отличаются на 6 %.

На рисунке 162 изображены соединенные между собой сосуды, называемые сообщающимися сосудами. Чайник, лейка (рис. 163) — примеры сообщающихся сосудов.

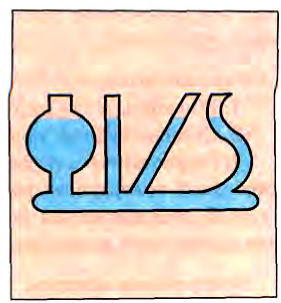Рис. 162

Рис. 163

Поверхность однородной жидкости в сообщающихся сосудах устанавливается на одном горизонтальном уровне. Это легко объяснить, пользуясь формулой (2). В покоящейся однородной жидкости давление на любом уровне в обоих сообщающихся сосудах одинаково.

Если же в сообщающихся сосудах находятся разнородные жидкости, то при равновесии уровни этих жидкостей не будут одинаковыми (рис. 164). Давление на уровне AA' при равновесии одинаково:

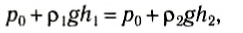
где p_o — внешнее давление, p₁ и р₂ — плотности жидкостей в сообщающихся сосудах. Из полученного соотношения следует

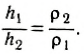
В сообщающихся сосудах высоты столбов жидкости над уровнем раздела жидкостей относятся обратно пропорционально плотностям этих жидкостей.

Главные выводы

1. Жидкость и газ находятся в сжатом состоянии.
2. Степень сжатия жидкости и газа характеризуется давлением.
3. Гидростатическое давление несжимаемой жидкости на глубине h от свободной поверхности равно p = pgh.
4. В сообщающихся сосудах уровень свободной поверхности одинаков для однородной жидкости и разный для разнородных жидкостей.