Числовые характеристики случайных величин - определение и примерами решения

Содержание:

Числовые характеристики случайных величин:

Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.

Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.

Математическое ожидание случайной величины

Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности: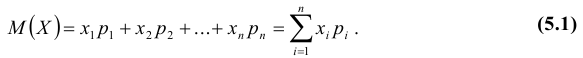

Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся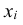

Рассмотрим свойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
2. Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
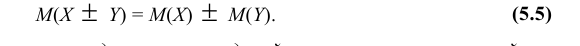
4. Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
5. Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

Пример:

Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.

Решение:

Используя свойства 1, 2, 3 математического ожидания, находим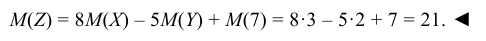

Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.

Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).

Дисперсия случайной величины

Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

Для дискретной случайной величины X эта формула принимает вид:

Для непрерывной случайной величины: 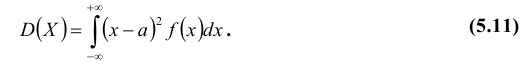На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: Для дискретной случайной величины X эта формула принимает вид: Для непрерывной случайной величины:

Рассмотрим свойства дисперсии.

1. Дисперсия постоянной величины равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
3. Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.

Пример №1

Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.

Решение:

Используя свойства дисперсии, находим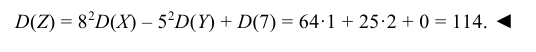

Среднее квадратическое отклонение случайной величины

Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину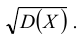

Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:

Свойства среднего квадратического отклонения вытекают из свойств дисперсии.

Мода и медиана. Квантили

Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.

Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 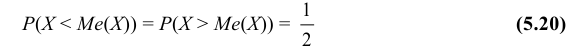т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.

Пример №2

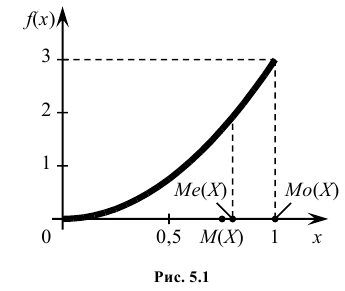
Найти моду, медиану случайной величины Х с плотностью вероятности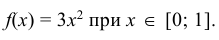

Решение:

Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 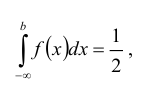или 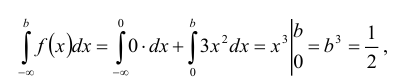откуда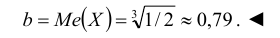

Наряду с модой и медианой для описания случайной величины используется понятие квантиля.

Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.

Пример №3

По данным примера 5.3 найти квантиль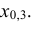

Решение:

Находим функцию распределения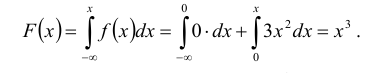

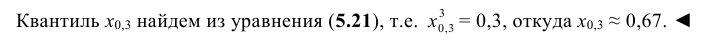
Моменты случайных величин. Асимметрия и эксцесс

Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.

Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: Для дискретной случайной величины формула начального момента имеет вид: Для непрерывной случайной величины:

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:

Для дискретной случайной величины формула центрального момента имеет вид:

Для непрерывной случайной величины: Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание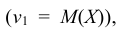при k = 2 второй центральный момент – дисперсия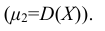

Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.

Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 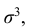, где σ – среднее квадратическое отклонение случайной величины Х.

Полученная величина А называется коэффициентом асимметрии случайной величины: Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.

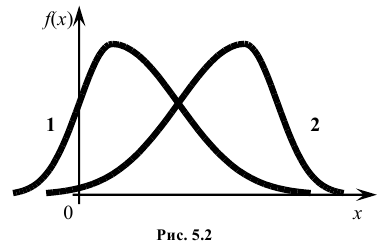
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).

Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом случайной величины называется число (Число 3 вычитается из отношения потому, что для нормального распределения, которое встречается наиболее часто, отношение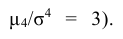 Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.

Числовые характеристики независимых испытаний

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)

Одинаково распределенные взаимно независимые случайные величины

Рассмотрим n взаимно независимых случайных величин 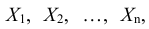которые имеют одинаковые распределения, а следовательно, одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляют числовые характеристики среднего арифметического этих величин.

Обозначим среднее арифметическое n взаимно независимых случайных величин через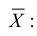

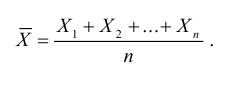
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 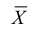и соответствующими характеристиками каждой отдельной величины.

1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в 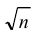раз меньше дисперсии D каждой из величин:
3. Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:

Пример:

По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.

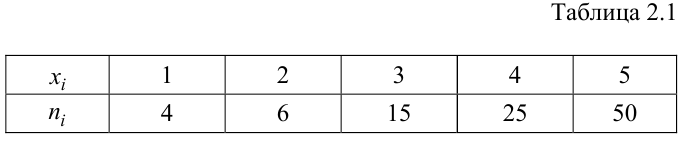
Решение. Определяем объем выборки: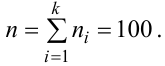 
Определяем относительные частоты вариант (табл. 2.2):  

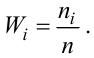
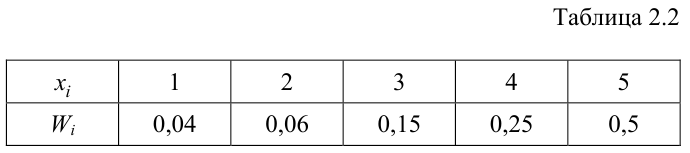
Так  как  значение 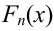   есть  сумма  относительных  частот вариант 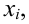попадающих в интервал  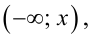запишем эмпирическую функцию распределения:

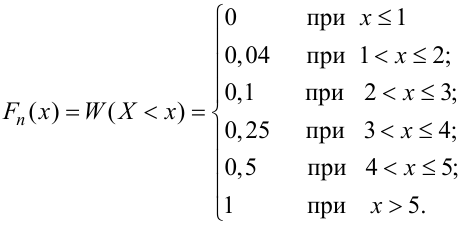
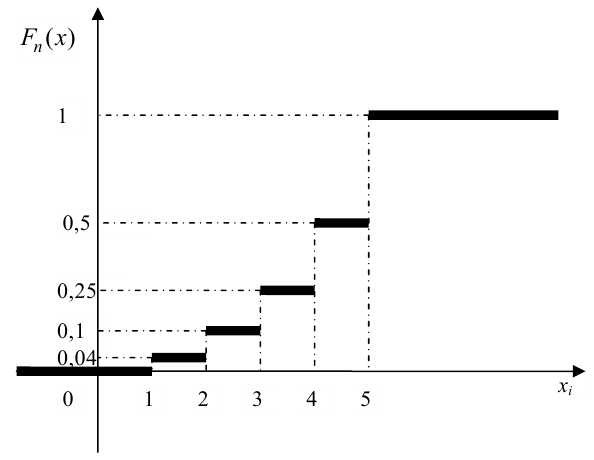
График примет вид: