Четырехугольники и окружность - задачи с примерами решения

Пример №1

Точка С — середина дуги АВ окружности меньшей полуокружности. Через точку С проведены хорды CD и CF, которые пересекают хорду АВ в точках К и Т соответственно. Докажите, что около четырехугольника DKTF можно описать окружность (рис. 114, а, б).
 

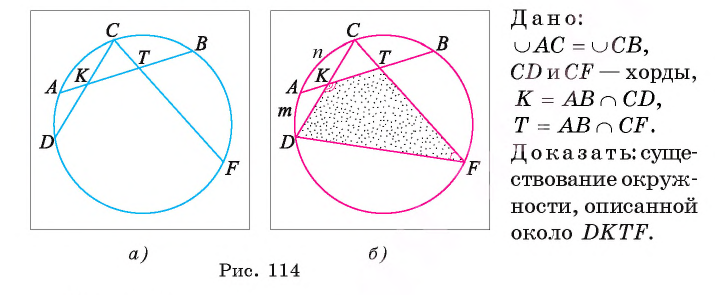
Пример №2

Диагонали АС и BD выпуклого четырехугольника ABCD, пересекающиеся в точке О, разделяют его на треугольники, площади которых 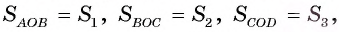Докажите, что верно равенство (рис. 115, a).

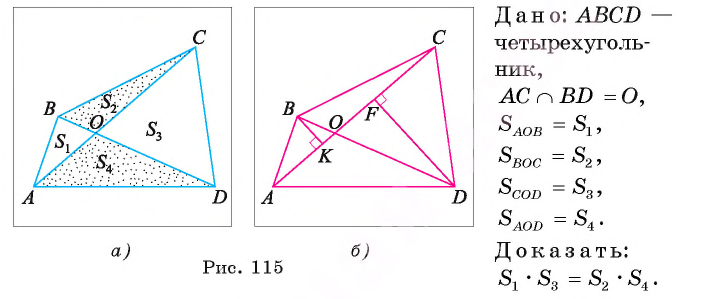
Решение:

1) Пусть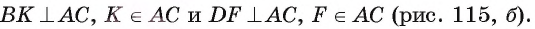

2) Треугольники АО В и ВОС имеют общую высоту ВК, следовательно,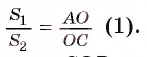  

3) Треугольники COD и AOD имеют общую высоту DF,

значит,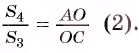

4) Из равенств (1) и (2) следует, что 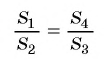или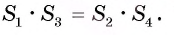  

Что и требовалось доказать.

Пример №3

Длины оснований AD и ВС трапеции ABCD равны соответственно а и b. Через точку F, принадлежащую стороне АВ и делящую ее в отношении т '■ п, считая от точки А, проведена прямая, параллельная основаниям трапеции и пересекающая сторону CD в точке Т. Докажите, что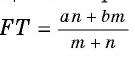

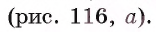
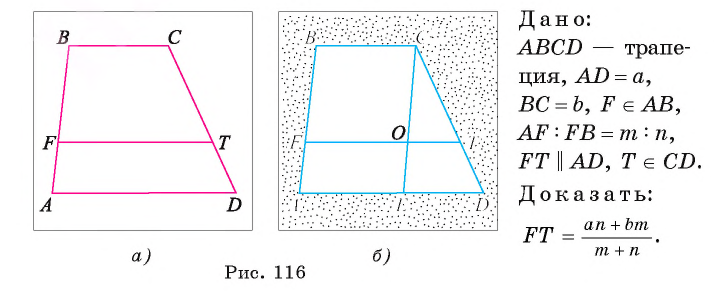
Решение:

1) Проведем отрезок СЕ, параллельный стороне АB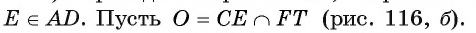

2) Так как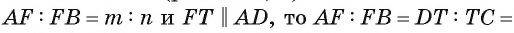 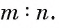Из условия СЕ || АВ следует, что ОТ = FT - b.

3) Треугольник СТО подобен треугольнику CDE, следовательно, 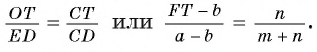Отсюда получим, что 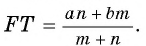Что и требовалось доказать.