Чертежи плоскости в начертательной геометрии с примерами

Чертежи плоскости:

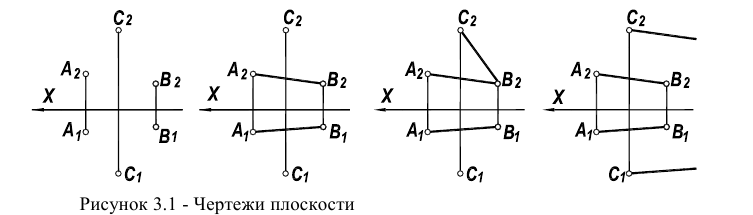
Симплексом, моделирующим плоскость, являются три точки, не лежащие на одной прямой, образующие треугольник. Для формирования этого объекта достаточно к симплексу прямой (отрезку) добавить точку, не лежащую на этой прямой. Таким образом, на чертеже плоскость может быть представлена проекциями трех точек (тремя парами соответственных точек). Эти точки могут объединиться в различные конфигурации: три отдельные точки, прямую и точку (взятую вне этой прямой), две пересекающиеся или параллельные прямые (рисунок 3.1).

До некоторой степени особняком стоит способ представления плоскости на чертеже с помощью следов. Следами

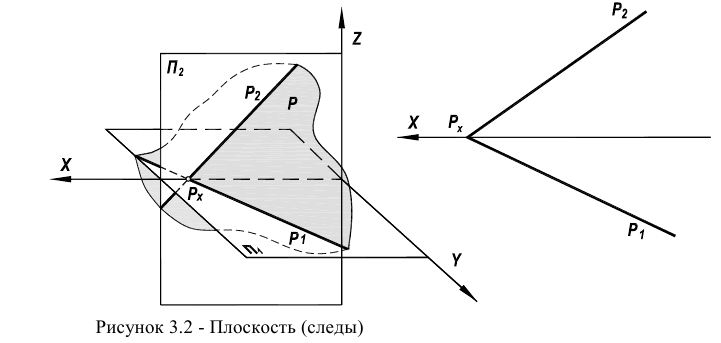
Рисунок 3.2 - Плоскость (следы)

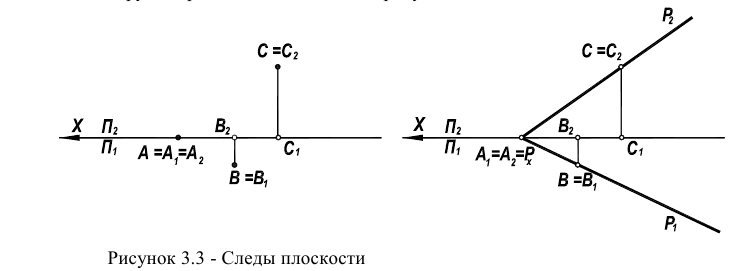
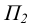Задание плоскости следами - это частный случай представления плоскости тремя точками, когда одна точка A лежит на оси Ох, вторая В - в плоскости проекции , а третья С - в плоскости проекции  (в соответствии с рисунком 3.3).

Следовательно, задание плоскости следами можно рассматривать как задание пересекающимися прямыми АС и АВ.

Фронтальный след 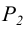в этом случае ничто иное, как фронтальная проекция 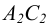- одной прямой, а горизонтальный след 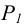- горизонтальная проекция AjBj- другой прямой, как показано на рисунке 3.3

Все плоскости трехмерного Евклидова пространства (по аналогии с прямой) можно классифицировать по их расположению по отношению к плоскостям проекции.

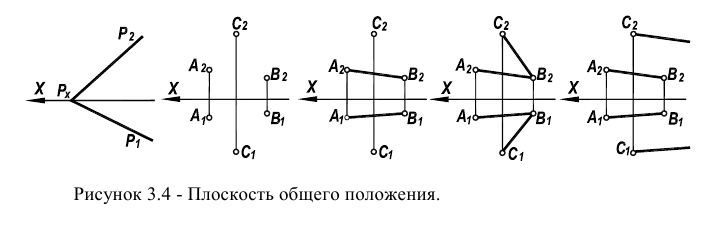
Плоскость, не параллельная и не перпендикулярная ни одной плоскости проекций (также, как и прямая), называется плоскостью общего положения (рисунок 3.4)

Характерным для чертежей такой плоскости является то, что ее оба следа являются линиями общего положения При задании плоскости симплексом обе проекции треугольника невырожденные.

Плоскость, перпендикулярная одной из плоскостей проекции (также, как и прямая), называется проецирующей плоскостью (рисунки 3.5, 3.6).

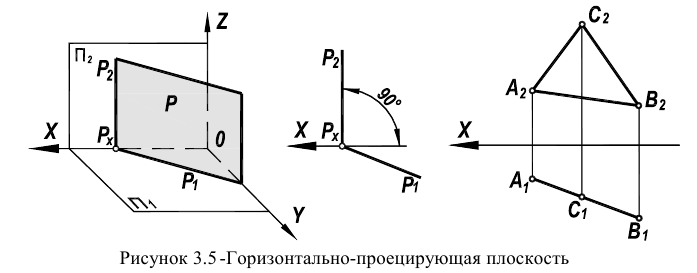
Плоскость, перпендикулярная горизонтальной плоскости проекций 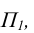называется горизонтально - проецирующей плоскостью (рисунок 3.5). Горизонтальная проекция симплекса 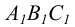у нее вырождается в прямую линию. При задании следами фронтальный след занимает положение фронтально проецирующей прямой 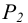(перпендикулярен оси чертежа).

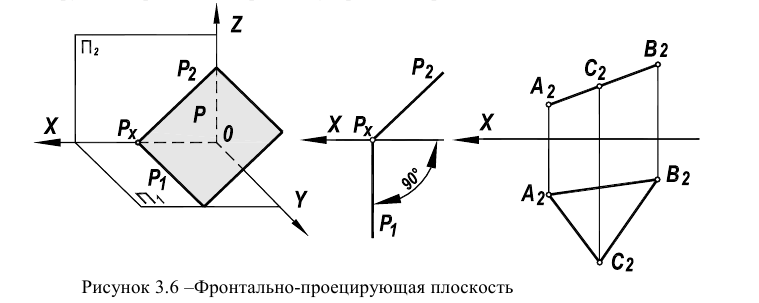
Плоскость, перпендикулярная фронтальной плоскости проекций называется фронтально - проецирующей плоскостью (рисунок 3.6). Фронтальная проекция симплекса у нее вырождается в прямую линию. При задании следами горизонтальный след занимает положение фронтально проецирующей прямой (перпендикулярен оси чертежа).

• Заказать чертежи

На чертеже, характерным признаком проецирующей плоскости является вырождение симплекса в прямую линию (при задании плоскости симплексом) или же перпендикулярность одного из следов оси чертежа (при задании следами).

Плоскость, параллельная одной из плоскостей проекции (также, как и прямая ), называется плоскостью уровня (рисунки 3.7, 3.8).

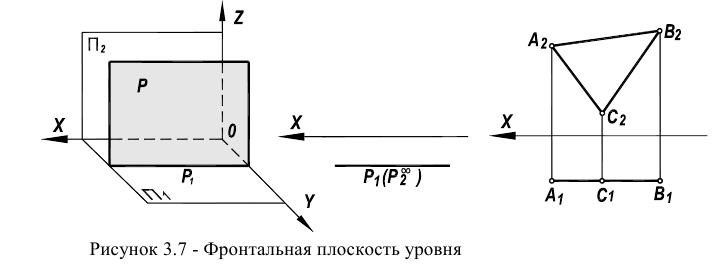
Плоскость, параллельная фронтальной плоскости проекций 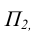называется фронтальной плоскостью уровня (рисунок 3.7). Горизонтальная проекция симплекса 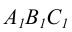у нее вырождается в прямую линию, параллельную оси чертежа, фронтальная проекция 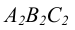представляется в неискаженном виде. При задании следами горизонтальный след 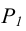занимает положение параллельное оси чертежа. Фронтальный след 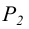в силу того, что 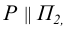становится несобственной прямой.

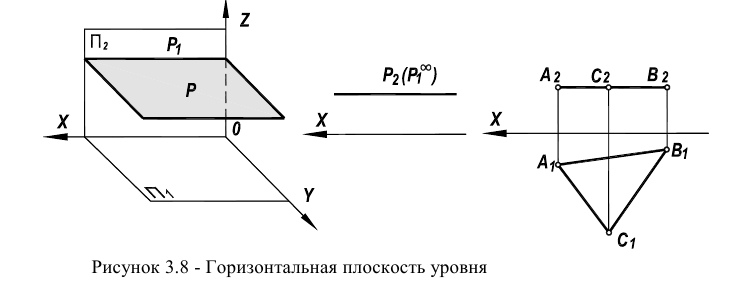
Плоскость, параллельная горизонтальной плоскости проекций 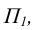называется горизонтальной плоскостью уровня (рисунок 3.8). Фронтальная проекция симплекса 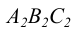у нее вырождается в прямую линию, параллельную оси чертежа, горизонтальная проекция 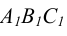представляется в неискаженном виде. При задании следами фронтальный след 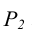занимает положение параллельное оси чертежа. Горизонтальный след 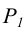в силу того, что 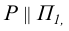становится несобственной прямой.

Характерным признаком плоскости уровня (на чертеже) является вырождение симплекса в прямую линию, параллельную оси чертежа (при задании плоскости симплексом) или же параллельность одного из следов оси чертежа (при задании следами).

Вопрос о взаимном расположении плоскостей в пространстве решается однозначно - плоскости пересекаются по прямой линии. В частном случае параллельные плоскости пересекаются по несобственной прямой.