
Бесконечно убывающая геометрическая прогрессия с примерами решения
Содержание:
Определение:
Геометрическая прогрессия со знаменателем 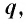
Примеры бесконечно убывающих геометрических прогрессий
Приведем примеры бесконечно убывающих геометрических прогрессий.
Пример №1
Последовательность
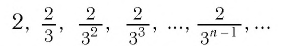
является бесконечно убывающей геометрической прогрессией с
первым членом 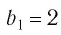 и знаменателем
и знаменателем 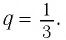
Пример №2
Последовательность
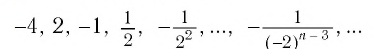
является бесконечно убывающей геометрической прогрессией с первым членом 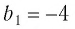 и знаменателем
и знаменателем 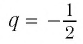 (здесь
(здесь 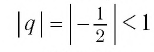 ). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).
). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).

Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением 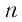 этот модуль становится меньше любого заданного положительного числа.
этот модуль становится меньше любого заданного положительного числа.
Например, если мы зададим число 0,01, то
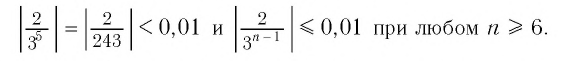
Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).

И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.
Например, если мы зададим число 0,001, то 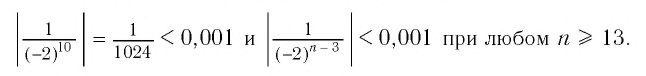 Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии
Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии 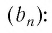 чем больше номер п члена прогрессии
чем больше номер п члена прогрессии 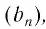 тем меньше
тем меньше 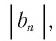 и с увеличением
и с увеличением 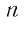 этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:
этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:
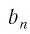 стремится к нулю при
стремится к нулю при 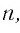 стремящемся к бесконечности.
стремящемся к бесконечности.
Заметим, что если 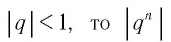 стремится к нулю при
стремится к нулю при 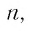 стремящемся к бесконечности.
стремящемся к бесконечности.
Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членом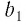 и знаменателем
и знаменателем 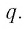
Запишем формулу суммы первых 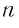 членов этой прогрессии и преобразуем это выражение:
членов этой прогрессии и преобразуем это выражение: 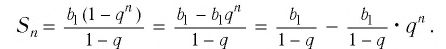 Обозначим
Обозначим
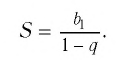
Тогда получим
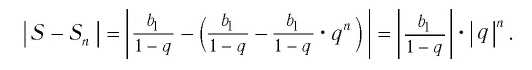
Так как 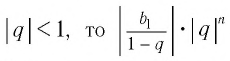 стремится к нулю при
стремится к нулю при 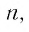 стремящемся к бесконечности. Значит,
стремящемся к бесконечности. Значит, 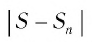 стремится к нулю при
стремится к нулю при 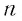 , стремящемся к бесконечности, т. е. чем больше число
, стремящемся к бесконечности, т. е. чем больше число 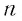 (чем больше слагаемых в сумме
(чем больше слагаемых в сумме 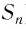 ), тем меньше разница между
), тем меньше разница между 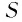 и
и 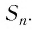 Поэтому число
Поэтому число 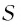 называют суммой бесконечно убывающей геометрической прогрессии.
называют суммой бесконечно убывающей геометрической прогрессии.
Пример №3
Найти сумму бесконечно убывающей геометрической прогрессии:
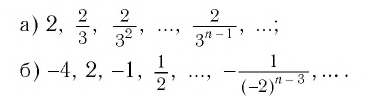
Решение:
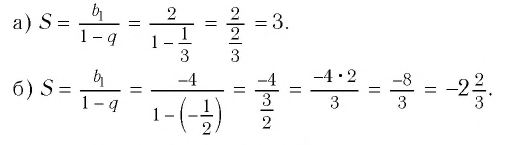
Ответ: 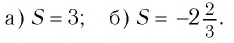
Всё о бесконечно убывающей геометрической прогрессии
Пример:
Рассмотрим квадрат со стороной 1 (рис. 57). Если середины его противоположных сторон соединить отрезком, то возникнут два прямоугольника с площадью 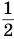 .
.
Если теперь середины одного из полученных прямоугольников соединить отрезком, то получится два прямоугольника с площадью 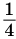 . Снова повторив такое действие, получим два прямоугольника с площадью
. Снова повторив такое действие, получим два прямоугольника с площадью 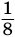 . Будем продолжать этот процесс далее. В результате получим бесконечную убывающую последовательность
. Будем продолжать этот процесс далее. В результате получим бесконечную убывающую последовательность
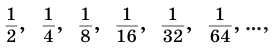
у которой каждый следующий член получается из предыдущего умножением на 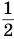 .
.
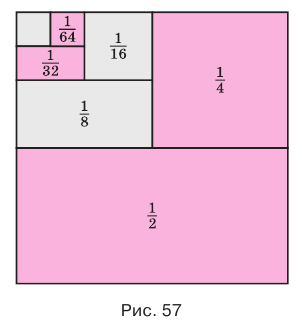
Естественно считать, что сумма 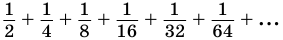 равна 1, так как она представляет площадь всего данного квадрата.
равна 1, так как она представляет площадь всего данного квадрата.
Записанная сумма содержит бесконечно много слагаемых. Рассмотрим ее часть 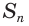 из
из 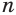 слагаемых:
слагаемых:
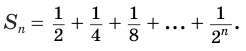
Ее компоненты образуют геометрическую прогрессию со знаменателем 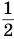 . Поэтому
. Поэтому
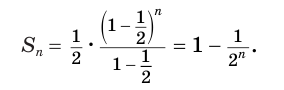
С возрастанием значения переменной 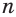 значение выражения
значение выражения 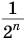 становится все меньше и меньше: значение переменной
становится все меньше и меньше: значение переменной 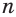 всегда можно подобрать так, что значение выражения
всегда можно подобрать так, что значение выражения 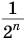 станет меньше любого малого заранее выбранного числа. Поэтому бесконечную сумму
станет меньше любого малого заранее выбранного числа. Поэтому бесконечную сумму 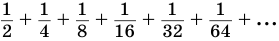 считают равной 1.
считают равной 1.
Рассмотрим теперь бесконечную геометрическую прогрессию
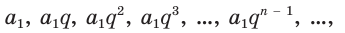
где 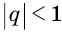 . Для таких прогрессий истинно условие
. Для таких прогрессий истинно условие 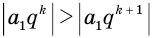 , их называют бесконечно убывающими геометрическими прогрессиями.
, их называют бесконечно убывающими геометрическими прогрессиями.
Сумма бесконечно убывающей геометрической прогрессии
Суммой членов бесконечно убывающей геометрической прогрессии 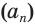 со знаменателем
со знаменателем 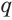 называется число
называется число 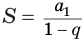 .
.
Это определение объясняется тем, что с увеличением 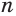 число
число 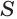 все меньше отличается от суммы первых
все меньше отличается от суммы первых 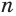 членов этой прогрессии. Действительно,
членов этой прогрессии. Действительно,
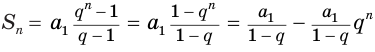 .
.
Поскольку 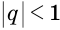 , то
, то 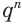 с увеличением
с увеличением 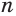 приближается к нулю, а значит, приближается к нулю и вычитаемое
приближается к нулю, а значит, приближается к нулю и вычитаемое 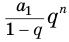 . Поэтому сумма
. Поэтому сумма 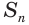 приближается к
приближается к 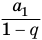 .
.
Пример №4
Найдем значение суммы 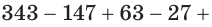
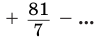 .
.
Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой 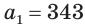 и
и 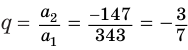 . Поэтому
. Поэтому
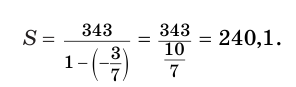
Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:
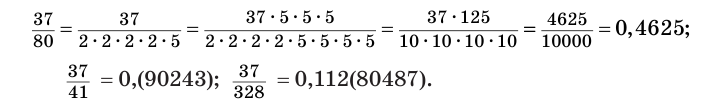
Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.
Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.
В дальнейшем мы будем пользоваться записью вида 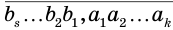 . Она обозначает десятичную дробь, целая часть которой записана с помощью цифр
. Она обозначает десятичную дробь, целая часть которой записана с помощью цифр 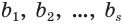 , а дробная — с помощью цифр
, а дробная — с помощью цифр 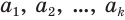 .
.
Теорема 7.
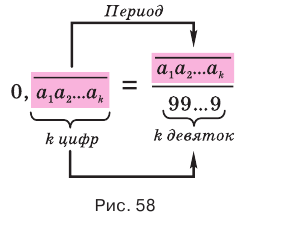
Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.
Доказательство:
Пусть 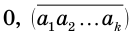 — периодическая десятичная дробь, где
— периодическая десятичная дробь, где 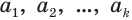 — цифры периода. Тогда число
— цифры периода. Тогда число 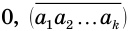 можно представить бесконечной суммой:
можно представить бесконечной суммой:
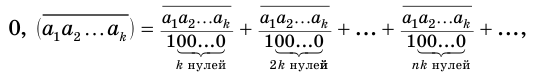
в которой каждое слагаемое получается из предыдущего умножением на 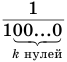 . Это означает, что бесконечную периодическую дробь можно рассматривать как сумму
. Это означает, что бесконечную периодическую дробь можно рассматривать как сумму 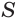 членов бесконечно убывающей геометрической прогрессии с первым
членов бесконечно убывающей геометрической прогрессии с первым
членом 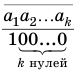 и знаменателем
и знаменателем 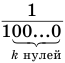 . Поэтому
. Поэтому
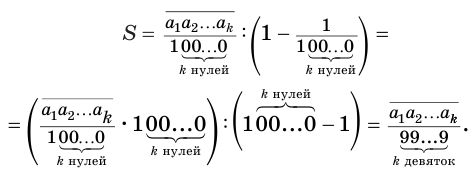
Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.
Пример №5
Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:
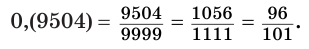
Теорема 8.
Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.
Доказательство:
Пусть 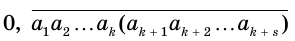 — периодическая десятичная дробь, где
— периодическая десятичная дробь, где 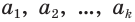 — цифры предпериода,
— цифры предпериода, 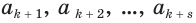 — цифры периода. Тогда число
— цифры периода. Тогда число 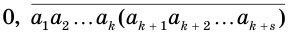 можно представить суммой
можно представить суммой
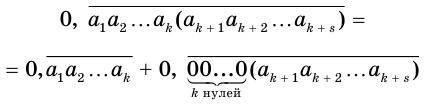
или, с учетом теоремы 7, суммой
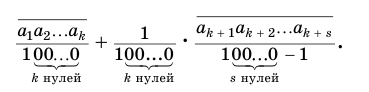
Преобразуем полученное выражение:
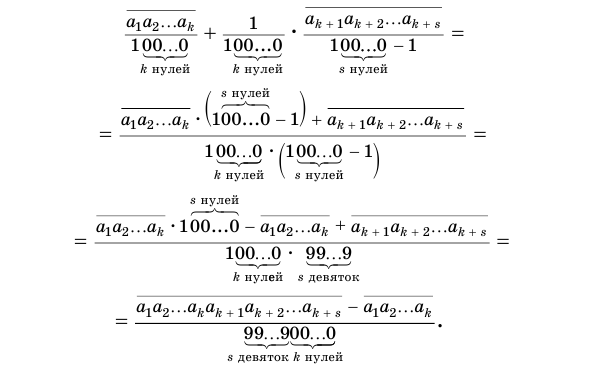
Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом, который отражен на схеме, представленной на рисунке 59.
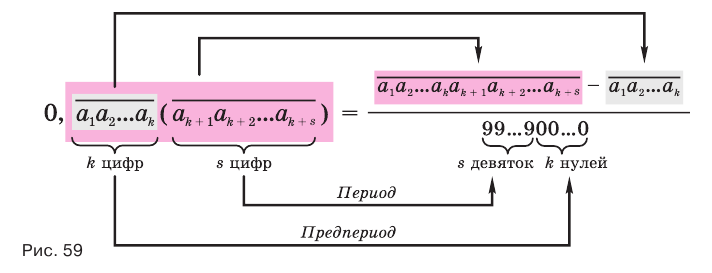
Пример №5
Представим обыкновенной дробью десятичную дробь 0,3213(513). Имеем:
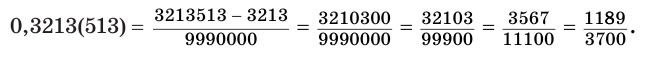
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |