
Бесконечно малые и бесконечно большие функции с примерами решения
Содержание:
Бесконечно малые и бесконечно большие функции
Бесконечно малые функции и их свойства
Определение: Функция 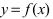
Пример:
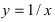 - бесконечно малая функция при
- бесконечно малая функция при 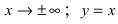 - бесконечно малая функция при
- бесконечно малая функция при 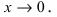
Решение:
Рассмотрим свойства бесконечно малых функций:
1. Сумма (разность) конечного числа бесконечно малых функций есть бесконечно малая функция.
Доказательство: Пусть 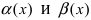 две бесконечно малые функции при
две бесконечно малые функции при 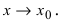 Это означает, что для любого сколь угодно малого положительного числа
Это означает, что для любого сколь угодно малого положительного числа 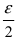 найдутся такие
найдутся такие 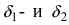 -окрестности точки
-окрестности точки 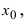 что будут выполняться неравенства
что будут выполняться неравенства 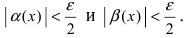 Следовательно,
Следовательно, 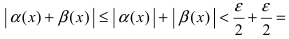
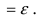 Полученное неравенство справедливо в меньшей из
Полученное неравенство справедливо в меньшей из 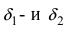 -окрестности точки
-окрестности точки 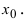 Кроме того, полученное неравенство свидетельствует о том, сумма двух бесконечно малых функций есть бесконечно малая функция.
Кроме того, полученное неравенство свидетельствует о том, сумма двух бесконечно малых функций есть бесконечно малая функция.
Замечание: Используя метод математической индукции можно доказать утверждение свойства 1. для любого конечного числа n слагаемых бесконечно малых функций.
Пример:
Является сумма бесконечно малых функций 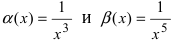 при
при 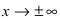 бесконечно малой функцией.
бесконечно малой функцией.
Решение:
Да, является, так как 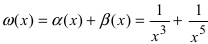 стремится к нулю при
стремится к нулю при 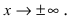 Нижеприведенные свойства бесконечно малых функций приведем без доказательства, так как они доказываются аналогично свойству 1.
Нижеприведенные свойства бесконечно малых функций приведем без доказательства, так как они доказываются аналогично свойству 1.
2. Произведение бесконечно малых фу нкций есть бесконечно малая функция.
3. Если функция 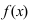 имеет при
имеет при 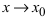 конечный предел
конечный предел 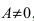 , частное отделения бесконечно малой функции на функцию
, частное отделения бесконечно малой функции на функцию 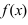 есть бесконечно малая функция.
есть бесконечно малая функция.
4. Если функция 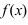 имеет при
имеет при 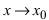 конечный предел A, то в некоторой
конечный предел A, то в некоторой 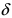 -окрестности точки
-окрестности точки 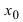 ее можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции
ее можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции 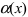 , т.е.
, т.е. 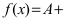
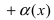 .
.
5. (обратное к 4.). Если в некоторой 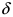 -окрестности точки
-окрестности точки 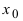 фу нкцию
фу нкцию 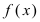 можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции
можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции 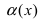 ,т.е.
,т.е. 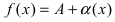 , то число А является пределом данной функции.
, то число А является пределом данной функции.
Замечание: Если функция 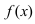 имеет при
имеет при 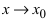 конечный предел А, то в некоторой
конечный предел А, то в некоторой 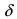 -окрестности точки
-окрестности точки 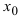 она ограничена. Если
она ограничена. Если 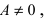 то в той же окрестности будет ограничена и функция
то в той же окрестности будет ограничена и функция 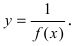 6. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.
6. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.
7. Отношение бесконечно малой функции к ограниченной функции есть бесконечно малая функция.
Бесконечно большие функции
Определение: Функция 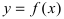 называется бесконечно большой при
называется бесконечно большой при 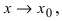 если ее предел при этом равен
если ее предел при этом равен 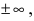 т.е.
т.е. 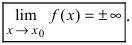
Пример:
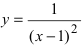 - бесконечно большая функция при
- бесконечно большая функция при 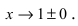 Построим график этой функции в некоторой окрестности точки
Построим график этой функции в некоторой окрестности точки 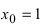 (Рис. 60):
(Рис. 60): 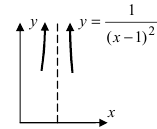
Решение:
График функции у = 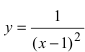 в малой окрестности точки
в малой окрестности точки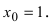
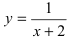 - бесконечно большая функция при
- бесконечно большая функция при 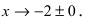 Покажем поведение этой функции в некоторой окрестности точки
Покажем поведение этой функции в некоторой окрестности точки 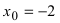 (Рис. 61):
(Рис. 61):
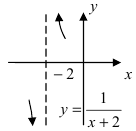 Рис. 61. График функции
Рис. 61. График функции 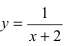 в малой окрестности точки
в малой окрестности точки 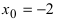 . Рассмотрим свойства бесконечно больших функций:
. Рассмотрим свойства бесконечно больших функций:
1. Сумма бесконечно больших при 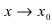 функций есть бесконечно большая функция.
функций есть бесконечно большая функция.
Замечание: При вычислении разности бесконечно больших функций может получиться любое вещественное число.
2. Произведение бесконечно больших функций есть бесконечно большая функция.
Замечание: При вычислении отношения бесконечно больших функций может получиться любое вещественное число.
3. Произведение бесконечно большой функции на ограниченную функцию есть бесконечно большая функция.
35. Вычисление произведения бесконечно большой функции на бесконечно малую функцию может привести к любому вещественному числу.
4. Отношение бесконечно большой функции к ограниченной функции есть бесконечно большая функция.
Установим связь между бесконечно большими и бесконечно малыми функциями, которая дается следующими теоремами:
Теорема: Если в некоторой 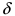 -окрестности точки
-окрестности точки 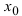 функция
функция 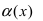 является бесконечно малой функцией, то в этой же окрестности функция
является бесконечно малой функцией, то в этой же окрестности функция 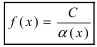 (
(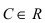 ) будет бесконечно большой функцией.
) будет бесконечно большой функцией.
Теорема: Если в некоторой 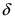 -окрестности точки
-окрестности точки 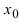 функция
функция 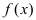 является бесконечно большой функцией, то в этой же окрестности функция
является бесконечно большой функцией, то в этой же окрестности функция 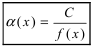 (
(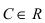 ) будет бесконечно малой функцией.
) будет бесконечно малой функцией.
Эти теоремы очень часто применяются при вычислении пределов, содержащих бесконечно малые и бесконечно большие функции.
Основные теоремы о пределах
ТЗ. Пусть 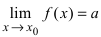 и
и 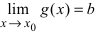 . Тогда
. Тогда 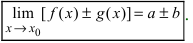
Доказательство: По свойству 4. для бесконечно малых функций в некоторой 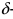 -окрестности точки
-окрестности точки 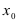 функции
функции 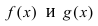 можно представить в виде:
можно представить в виде: 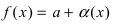 и
и 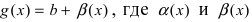 две бесконечно малые функции при
две бесконечно малые функции при 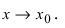 Найдем сумму (разность) функций
Найдем сумму (разность) функций 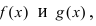 имеем
имеем 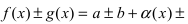
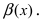 По свойству 1. для бесконечно малых функций величина
По свойству 1. для бесконечно малых функций величина 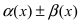 является бесконечно малой функцией, следовательно, по свойству 5. для бесконечно малых функций получим
является бесконечно малой функцией, следовательно, по свойству 5. для бесконечно малых функций получим 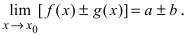
Замечание: Другими словами данную теорему можно сформулировать так: если функции 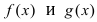 имеют конечные пределы а и b, то предел от суммы ( разности) будет равен сумме (разности) пределов от этих функций, т.е.
имеют конечные пределы а и b, то предел от суммы ( разности) будет равен сумме (разности) пределов от этих функций, т.е. 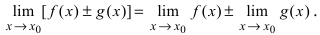
T4. Пусть 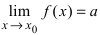 и
и 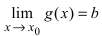 . Тогда
. Тогда 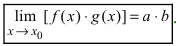
Доказательство: По свойству 4. для бесконечно малых функций в некоторой 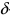 -окрестности точки
-окрестности точки 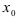 функции
функции 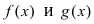 можно представить в виде:
можно представить в виде: 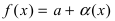 и
и 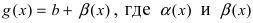 две бесконечно малые функции при
две бесконечно малые функции при 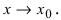 Найдем произведение функций
Найдем произведение функций 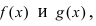 имеем
имеем 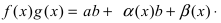
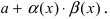 По свойству 2. для бесконечно малых функций величина
По свойству 2. для бесконечно малых функций величина 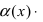
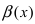 является бесконечно малой функцией. По свойству 1. для бесконечно малых функций величина
является бесконечно малой функцией. По свойству 1. для бесконечно малых функций величина 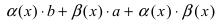 является бесконечно малой функцией, следовательно, по свойству 5 для бесконечно малых функций получим
является бесконечно малой функцией, следовательно, по свойству 5 для бесконечно малых функций получим 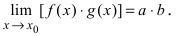
Замечание: Иначе данную теорему можно сформулировать так: если функции f(х) и g(x) имеют конечные пределы а и b, то предел от произведения функций будет равен произведению пределов от этих функций, т.е.
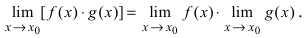
Теорема: Если в некоторой 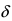 -окрестности точки
-окрестности точки 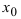 функция
функция 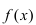 постоянна и равна С (
постоянна и равна С (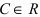 ), то ее предел равен С.
), то ее предел равен С.
Следствие: из теорем: если 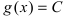 , тo
, тo 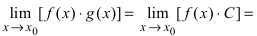
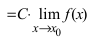 , т.е. постоянный множитель можно выносить за знак предела.
, т.е. постоянный множитель можно выносить за знак предела.
Следствие: Предел степени функции 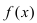 равен степени предела этой функции, т.е.
равен степени предела этой функции, т.е.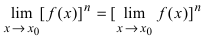
Тб. Пусть 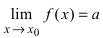 и
и 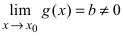 . Тогда
. Тогда 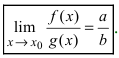
Доказательство: По свойству 4. для бесконечно малых функций в некоторой 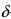 -окрестности точки
-окрестности точки 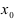 функции
функции 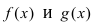 можно представить в виде:
можно представить в виде: 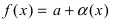 и
и 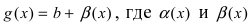 - две бесконечно малые функции при
- две бесконечно малые функции при 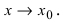
Рассмотрим выражение:
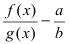 в
в 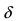 -окрестности точки
-окрестности точки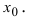 С учетом выше сказанного имеем
С учетом выше сказанного имеем 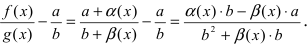 В числителе дроби стоит бесконечно малая функция (свойство 1 для бесконечно малых функций), а в знаменателе дроби стоит ограниченная функция. По свойству 7. для бесконечно малых функций дробь в целом представляет собой бесконечно малую функцию
В числителе дроби стоит бесконечно малая функция (свойство 1 для бесконечно малых функций), а в знаменателе дроби стоит ограниченная функция. По свойству 7. для бесконечно малых функций дробь в целом представляет собой бесконечно малую функцию 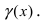 Следовательно, в
Следовательно, в 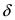 -окрестности точки
-окрестности точки 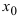 отношение функций
отношение функций 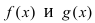 может быть представлено в виде
может быть представлено в виде 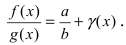 Отсюда по свойству 5. для бесконечно малых функций получим, что
Отсюда по свойству 5. для бесконечно малых функций получим, что 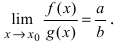
Замечание: Сформулируем теорему иначе: если функции 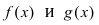 имеют конечные пределы
имеют конечные пределы 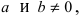 то предел от отношения функций будет равен отношению пределов от этих функций, т.е.
то предел от отношения функций будет равен отношению пределов от этих функций, т.е. 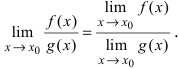
Вычисление пределов и раскрытие неопределенностей
Вычисление любых пределов начинается с подстановки предельного значения аргумента 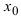 в подлимитную функцию
в подлимитную функцию 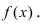 Если при этом полу- чается число, то это число и будет пределом данной функции.
Если при этом полу- чается число, то это число и будет пределом данной функции.
Пример:
Вычислить 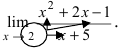
Решение:
Подставим в функцию значение 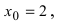 получим
получим 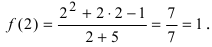 Таким образом,
Таким образом, 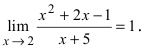
Пример:
Вычислить 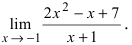
Решение:
Если подставить в функцию предельное значение 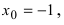 то числитель дроби стремится к
то числитель дроби стремится к 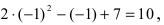 а знаменатель дроби стремится к
а знаменатель дроби стремится к 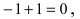 т.е. в некоторой
т.е. в некоторой 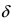 -окрестности точки
-окрестности точки 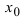 является бесконечно малой функцией. Воспользуемся теоремой, величина обратная к бесконечно малой функции есть бесконечно большая функция, предел которой равен бесконечности. Следовательно,
является бесконечно малой функцией. Воспользуемся теоремой, величина обратная к бесконечно малой функции есть бесконечно большая функция, предел которой равен бесконечности. Следовательно, 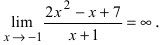
Определение: Если при подстановки предельного значения аргумента 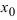 в подлимитную функцию возникают выражения вида
в подлимитную функцию возникают выражения вида 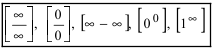 и им подобные, то говорят о наличии неопределенности.
и им подобные, то говорят о наличии неопределенности.
Определение: Процесс нахождения пределов, имеющих неопределенность, называется раскрытием неопределенностей.
Рассмотрим некоторые приемы раскрытия неопределенностей:
1. Неопределенность типа  возникающая при вычислении предела от отношения двух полиномов при
возникающая при вычислении предела от отношения двух полиномов при  раскрывается путем деления числителя и знаменателя на аргумент в высшей степени и использования теореме о связи б.б.ф. с б.м.ф., предел которой равен 0.
раскрывается путем деления числителя и знаменателя на аргумент в высшей степени и использования теореме о связи б.б.ф. с б.м.ф., предел которой равен 0.
Пример:
Найти 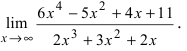
Решение:
При 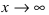 и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида
и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 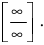 Высший показатель степени равен 4 и находится в числителе дроби. Разделим числитель и знаменатель дроби на
Высший показатель степени равен 4 и находится в числителе дроби. Разделим числитель и знаменатель дроби на 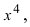 получим
получим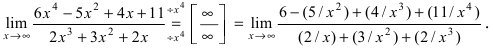
Все дроби по теореме при 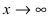 стремятся к 0, следовательно, числитель стремится к 6, а знаменатель - к 0. Используя теорему о связи б.м.ф. с б.б.ф., предел которой равен
стремятся к 0, следовательно, числитель стремится к 6, а знаменатель - к 0. Используя теорему о связи б.м.ф. с б.б.ф., предел которой равен 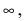 окончательно получим, что
окончательно получим, что 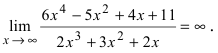
Пример:
Найти 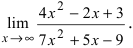
Решение:
При 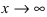 и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида
и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 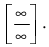 Высший показатель степени равен 2 и находится в числителе и знаменателе дроби. Разделим числитель и знаменатель дроби на
Высший показатель степени равен 2 и находится в числителе и знаменателе дроби. Разделим числитель и знаменатель дроби на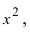 получим
получим 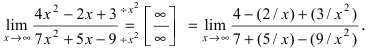 Все дроби по теореме при
Все дроби по теореме при 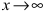 стремятся к 0, следовательно, числитель стремится к 4, а знаменатель - к 7. Следовательно,
стремятся к 0, следовательно, числитель стремится к 4, а знаменатель - к 7. Следовательно, 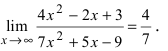
Пример:
Найти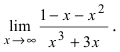
Решение:
При 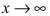 и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида
и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 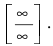 Высший показатель степени равен 3 и находится в знаменателе дроби. Разделим числитель и знаменатель дроби на
Высший показатель степени равен 3 и находится в знаменателе дроби. Разделим числитель и знаменатель дроби на 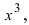 получим
получим 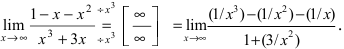 Все дроби по теореме при
Все дроби по теореме при 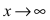 стремятся к 0, следовательно, числитель стремится к 0, а знаменатель - к 1. Следовательно,
стремятся к 0, следовательно, числитель стремится к 0, а знаменатель - к 1. Следовательно, 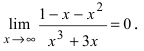
Рассмотренные примеры позволяют сделать следующий вывод: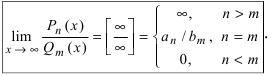
2. Неопределенность типа 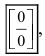 возникающая при вычислении предела от отношения двух полиномов при
возникающая при вычислении предела от отношения двух полиномов при 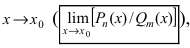 раскрывается путем разложения полимонов на простые множители и дальнейшего сокращения числителя и знаменателя дроби на обнуляющий их множитель
раскрывается путем разложения полимонов на простые множители и дальнейшего сокращения числителя и знаменателя дроби на обнуляющий их множитель 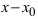 (при этом используются формулы
(при этом используются формулы 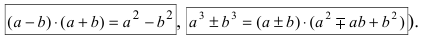
Пример:
Найти 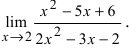
Решение:
Подстановка предельного значения аргумента 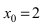 в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности
в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности 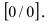 Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на простые множители, для чего решим следующие уравнения:
Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на простые множители, для чего решим следующие уравнения: 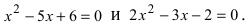 По теореме Виета находим
По теореме Виета находим 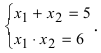 Следовательно,
Следовательно, 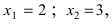 а разложение полинома имеет вид:
а разложение полинома имеет вид: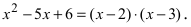 Решим уравнение:
Решим уравнение:
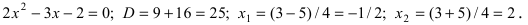
Следовательно, разложение этого полинома на простые множители будет иметь вид: 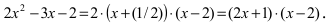 Подставим найденные разложения полиномов в исходный предел, получим
Подставим найденные разложения полиномов в исходный предел, получим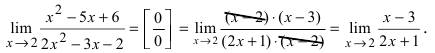
Подставляя вместо переменной х ее предельное значение 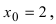 получим ответ:
получим ответ: 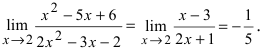
3. Неопределенность типа 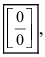 возникающая при вычислении предела, со- держащего квадратные корни, при
возникающая при вычислении предела, со- держащего квадратные корни, при 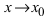 раскрывается с использованием фор- мулы, определяющей разность квадратов
раскрывается с использованием фор- мулы, определяющей разность квадратов 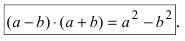
Пример:
Найти 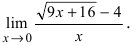
Решение:
Подстановка предельного значения аргумента 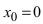 в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности
в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности 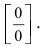 Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение
Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение 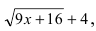 получим:
получим: 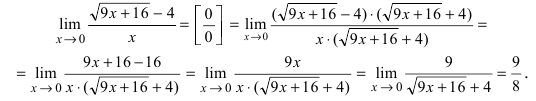
Пример:
Найти 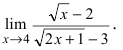
Решение:
Устремляя х к 4, получим неопределенность 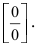 Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение
Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение 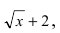 а знаменатель и числитель дроби на выражение
а знаменатель и числитель дроби на выражение 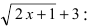
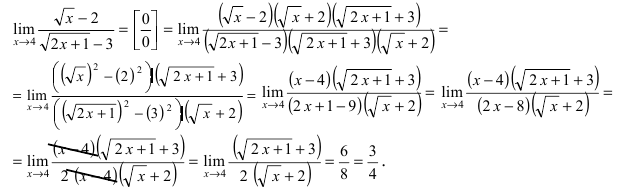
Пример:
Найти 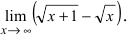
Решение:
Устремляя x к бесконечности, получим неопределенность 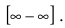 Умножим числитель и знаменатель дроби на выражение
Умножим числитель и знаменатель дроби на выражение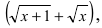 получим
получим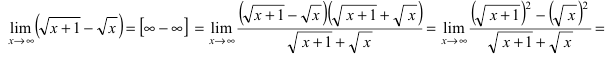
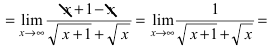 (знаменатель дроби стремится к бесконечности, следовательно, дробь по теореме при
(знаменатель дроби стремится к бесконечности, следовательно, дробь по теореме при 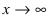 стремится к
стремится к 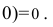
-----вышмат
Бесконечно малые и бесконечно большие функции
Математическая интерпретация явления часто заключается в том, что практически очень малые величины принимаются за бесконечно малые. Так, рассматривая годовое производство, мы можем отдельный день представить себе как бесконечно малую частицу годового периода и получать при этом практически верные результаты.
Функция y=f(x) называется бесконечно малой при 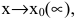 если ее предел равен нулю:
если ее предел равен нулю: 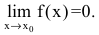
Функция y=f(x) называется бесконечно большой при 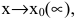 если ее предел равен бесконечности:
если ее предел равен бесконечности: 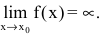
Между бесконечно малыми и бесконечно большими функциями существует связь: если f(x) - бесконечно малая функция при 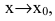 то
то 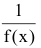 - бесконечно большая функция при
- бесконечно большая функция при 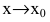 и наоборот.
и наоборот.
Теорема 1. Алгебраическая сумма и произведение конечного числа бес-
конечно малых функций при 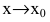 есть бесконечно малая функция при
есть бесконечно малая функция при 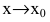 .
.
Теорема 2. Произведение бесконечно малой при 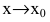 функции на ограниченную есть бесконечно малая функция при
функции на ограниченную есть бесконечно малая функция при 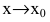 .
.
Пример №28
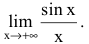
Решение:
Т.к. sinx - ограниченная функция для любых 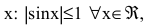
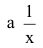 - бесконечно малая функция при
- бесконечно малая функция при 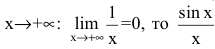 - бесконечно малая функция при
- бесконечно малая функция при 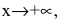 т.е.
т.е. 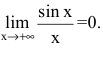
Если f(x) и g(x) - бесконечно малые функции при 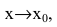 то
то 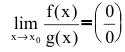 — может быть равен либо нулю, либо бесконечности, либо какому-нибудь числу, отличному от нуля; наконец, предел может не существовать.
— может быть равен либо нулю, либо бесконечности, либо какому-нибудь числу, отличному от нуля; наконец, предел может не существовать.
Если 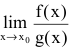 не существует, то f(x) и g(x) называют несравнимыми бесконечно малыми при
не существует, то f(x) и g(x) называют несравнимыми бесконечно малыми при 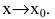
Если 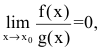 то функция f(x) стремится к нулю быстрее, чем g(x)
то функция f(x) стремится к нулю быстрее, чем g(x)
при 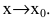 Говорят, что f(x) - бесконечно малая более высокого порядка, чем g(x) при
Говорят, что f(x) - бесконечно малая более высокого порядка, чем g(x) при 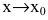 и пишут: f(x)=o(g(x)),
и пишут: f(x)=o(g(x)), 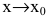 (читается «f(x) есть о малое от g(x) при
(читается «f(x) есть о малое от g(x) при 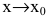 ).
).
Если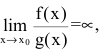 то f(x) называют бесконечно малой более низкого порядка, чем g(x) при
то f(x) называют бесконечно малой более низкого порядка, чем g(x) при 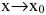 и пишут: g(x)=o(f(x)),
и пишут: g(x)=o(f(x)), 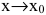 .
.
Если 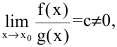 то f(x) и g(x) называют бесконечно малыми одного порядка при
то f(x) и g(x) называют бесконечно малыми одного порядка при 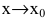 и пишут: f(x)=O(g(x)),
и пишут: f(x)=O(g(x)), 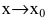 .
.
f ( X )
Особенно важен частный случай, когда 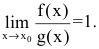 Тогда f(x) и g(x) называют эквивалентными бесконечно малыми при
Тогда f(x) и g(x) называют эквивалентными бесконечно малыми при 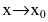 и пишут: f(x)~g(x),
и пишут: f(x)~g(x), 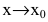 .
.
Пример №29
Показать, что 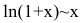 при
при 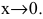
Решение:
Функции 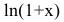 и х являются бесконечно малыми
и х являются бесконечно малыми 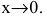 Найдем предел их отношения
Найдем предел их отношения 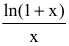 при
при 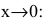
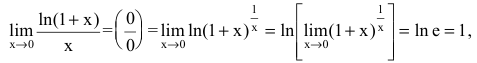 что и требовалось доказать. (Переход к пределу под символом логарифма возможен, т.к. логарифмическая функция непрерывна.)
что и требовалось доказать. (Переход к пределу под символом логарифма возможен, т.к. логарифмическая функция непрерывна.)
Утверждение. Если 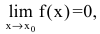 то
то 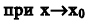 следующие функции экви- валентны:
следующие функции экви- валентны:  Данная цепочка эквивалентностей используется при нахождении преде- лов.
Данная цепочка эквивалентностей используется при нахождении преде- лов.
Теорема 3. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.
Пример №30
Вычислить предел 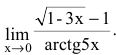
Решение:
Для нахождения предела используем свойства эквивалентности бесконечно малых функций: 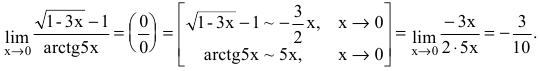
Пример №31
Вычислить предел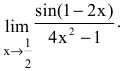
Решение:
Используя теорему об эквивалентных бесконечно малых, получаем: 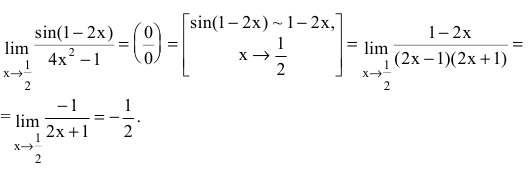
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат