Асимптотика схемы независимых испытаний - определение и вычисление с примерами решения

Локальная и интегральная теоремы Муавра–Лапласа:

При большом числе опытов n формула Бернулли (2.6.1) приводит к большому объему вычислений. Существуют приближенные формулы для вычисления вероятностей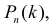

Пусть 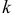– число появлений события A в 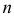независимых опытах, в каждом из которых 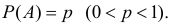Тогда при достаточно больших 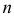(хотя бы несколько десятков) вероятность того, что в 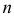независимых опытах событие A ровно 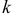раз, определяется формулой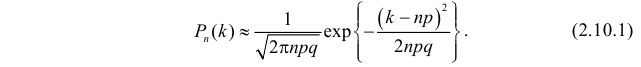

Эта формула составляет содержание локальной теоремы Муавра– Лапласа. Для вычисления вероятностей по формуле (2.10.1) удобно пользоваться таблицей функции 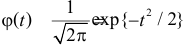(см. прил., табл. П1). Использование этой функции позволяет записать искомую вероятность в виде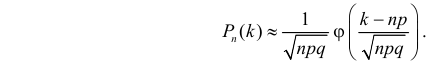 

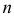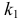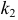Вероятность того, что в независимых опытах событие A появится от до раз, определяется формулой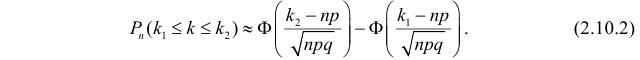 

Эта формула составляет содержание интегральной теоремы Муавра–Лапласа.

Замечание. Правая часть формулы (2.10.1) соответствует функции плотности вероятности нормального закона распределения 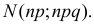Формула (2.10.2) является формулой (2.9.2), записанной для нормального закона распределения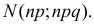

Пример:

Восемьдесят процентов приборов после сборки нуждаются в регулировке. Какова вероятность того, что среди 400 собранных за смену приборов в регулировке нуждаются: а) не менее 310; б) не более 350; в) от 304 до 336?

Решение. Сборку каждого прибора можно считать независимым испытанием с вероятностью появления события равной 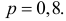 Так как число опытов велико, то можно воспользоваться интегральной теоремой Муавра–Лапласа (2.10.2):

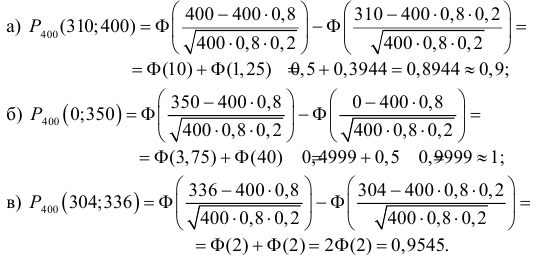
Ответ.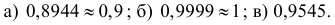 

Пример:

В страховой компании застраховано 10000 автомобилей. Вероятность поломки любого автомобиля в результате дорожно-транспортного происшествия равна 0,02. Каждый владелец застрахованного автомобиля платит в год 24 у.е. страховых и в случае поломки автомобиля в результате аварии получает от компании 1000 у.е. Найдите вероятность того, что по истечении года работы компания потерпит убытки от этого вида страховой деятельности.

Решение. Страховой сбор с 10000 владельцев автомобилей составляет 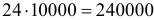у.е. Компания потерпит убытки, если будет предъявлено более 240 исков по 1000 у.е. каждый. Вероятность поступления страхового иска от каждого автовладельца равна 0,02. Эксплуатацию каждого автомобиля в течение страхового срока можно считать независимым испытанием. Так как число испытаний велико 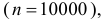то можно воспользоваться интегральной теоремой Муавра- Лапласа. По формуле (2.10.2)

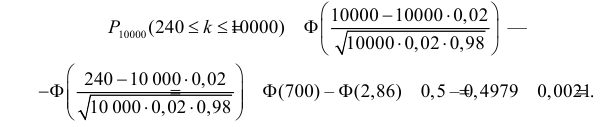
Ответ.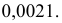 

Пример:

Вероятность попадания в цель при выстреле равна 0,8. Сколько нужно запланировать выстрелов, чтобы с вероятностью большей 0,9 можно было получить не менее 30 попаданий.

Решение. Каждый выстрел считаем независимым опытом. Из условий задачи легко видеть, что число выстрелов 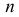должно быть достаточно большим 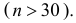Поэтому можно воспользоваться интегральной формулой Муавра–Лапласа (2.10.2):

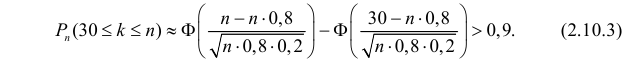
Заметим, что 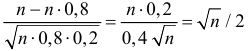 и при 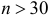 величина  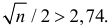Поэтому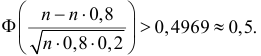 

В итоге неравенство (2.10.3) можно переписать в виде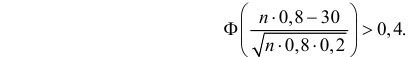 

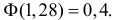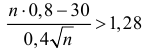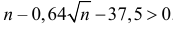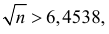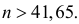По таблице функции Лапласа находим, что  Так как функция Лапласа строго возрастает, то или  Откуда т.е. Итак,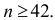

Ответ. 42.

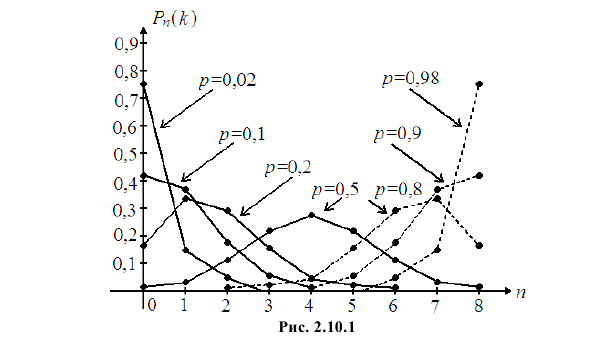
Замечание. При значениях 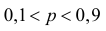формула Муавра–Лапласа (2.10.2) дает приближение приемлемой точности, так как многоугольник распределения при большом числе опытов напоминает по форме функцию плотности вероятности нормального закона распределения (см. рис. 2.10.1, на котором указаны вероятности 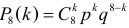при разных значениях ). 

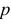Формула Пуассона

При значениях вероятности появления события близких к нулю или единице многоугольник распределения существенно несимметричен (см. рис. 2.10.1). Приближенная формула (2.10.1) не обеспечивает приемлемой точности. В этих условиях для вычисления вероятностей 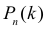используют обычно формулу Пуассона (2.10.4).

Пусть число независимых опытов 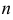велико (чем больше, тем лучше), а вероятность события 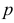мала (чем меньше, тем лучше, но 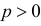). Тогда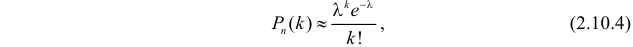

где 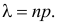 Эту формулу называют формулой Пуассона. Формула Пуассона дает приемлемую точность, если производится хотя бы несколько десятков опытов, а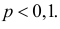

Пример:

Вероятность того, что изделие при транспортировке с завода повредится, равна 0,0005. С завода отправлено четыре тысячи изделий. Какова вероятность того, что в пути повредится больше двух изделий?

Решение. Транспортировку каждого изделия можно рассматривать как независимый опыт, число которых 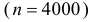велико. Вероятность же появления события в каждом опыте 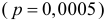мала. Это дает основание воспользоваться для вычислений формулой Пуассона (2.7.1). Заметим, что 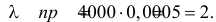Нас интересует вероятность

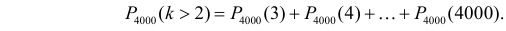
Проще эту вероятность вычислить, если рассмотреть вероятность противоположного события:

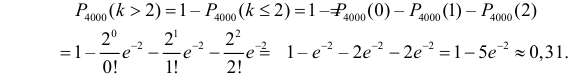
Ответ.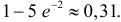 

Пример:

Известно, что из каждой 1000 элементов в среднем 999 сохраняют свою работоспособность в течение гарантийного срока. Какова вероятность того, что из 3000 элементов все до единого сохранят свою работоспособность в течение гарантийного срока?

Решение. Работу каждого элемента в течение гарантийного срока можно считать независимым опытом. Число опытов велико (n = 3000 ). Вероятность того, что элемент сохранит работоспособность в течение гарантийного срока, равна 0,999. Формула Бернулли (2.6.1) из-за большого числа опытов для расчетов неприемлема. Для применения формулы Пуассона будем говорить не о работоспособных элементах, а об элементах вышедших из строя. Вероятность выхода из строя элементам 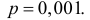 Тогда 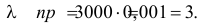Все 3000 элементов сохранят свою работоспособность, если ни один из них не выйдет из строя. По формуле Пуассона (2.7.1) 

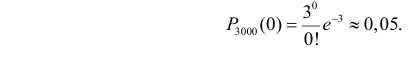
Ответ.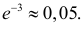 

Пример:

В студенческом строительном отряде работает 400 студентов. Вероятность того, что студент в течение всего срока работы получит травму, требующую введения противостолбнячной сыворотки, равна 0,005. Какое минимальное количество доз сыворотки должно быть в медсанпункте этого отряда, чтобы с вероятностью не менее 0,95 их хватило в случае необходимости?

Решение. Работу каждого студента в строительном отряде можно считать независимым опытом. Имеем большое число 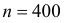опытов, а вероятность травмы 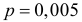– мала. Поэтому можно воспользоваться формулой Пуассона (2.7.1), в которой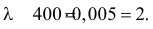

Минимальное количество доз можно найти как минимальное 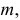при котором выполняется неравенство 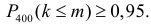Непосредственный подсчет по формуле (2.7.1) показывает, что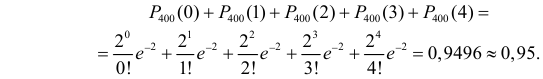

Заметим, что добавление к четырем еще одной дозы дает

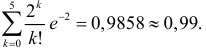
Ответ. 4.

Пример:

Предстоит произвести профилактический осмотр 400 устройств. Вероятность того, что в осматриваемом устройстве некоторый элемент потребуется заменить, равна 0,005. Какова вероятность того, что придется заменить не более четырех элементов?

Решение. Осмотр каждого устройства можно считать независимым опытом, и всего таких опытов планируется 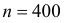. Вероятность замены детали 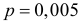– мала. Поэтому формула Муавра–Лапласа неприемлема. В этих условиях лучше воспользоваться асимптотической формулой Пуассона. Так как  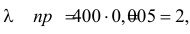то 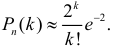 Поэтому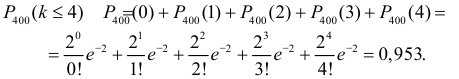 

Ответ. 0,953.