ARMA модель авторегрессии в экономике - обобщения, временные ряды и отстаивания

Содержание:

ARMA подходит, когда система является функцией серии неочевидных потрясений (МА или часть скользящей средней), а также ее собственное поведение. Таким образом, цены акций могут быть шокированы фундаментальной информацией, а также проявлением участниками рынка технических трендов и обратных эффектов.

Обобщения

Зависимость X t для прошлых значений и терминов ошибок ε t предполагается линейной, если не указано иное. Когда зависимость является нелинейной, модель специально называют нелинейной скользящей средней (NMA), нелинейной авторегрессией (NAR) или нелинейной авторегрессивной скользящей средней (NARMA).

Авторегрессивные модели скользящих средних могут быть обобщены другими способами. См. также модели авторегрессионной условной гетероскедастичности (ARCH) и авторегрессионной интегрированной скользящей средней (ARIMA). При необходимости установки нескольких временных рядов может быть установлена векторная модель ARIMA (или VARIMA). Если рассматриваемый временной ряд имеет длинную память, то может быть уместно дробное ARIMA-моделирование (FARIMA, иногда называемое ARFIMA): см. раздел Авторегрессивное дробное интегрированное скользящее среднее . Если предполагается, что данные содержат сезонные эффекты, то они могут быть смоделированы с помощью SARIMA (сезонная ARIMA) или периодической ARMA модели.

Другим обобщением является мультимасштабная модель авторегрессии (MAR). Модель MAR индексируется по узлам дерева, а стандартная (дискретно-временная) авторегрессионная модель индексируется целыми числами.

Обратите внимание, что модель ARMA является одномерной моделью. Расширения для многомерного корпуса - векторная авторегрессия (VAR) и векторная авторегрессия скользящих средних (VARMA). Сайт Википедии:wikichi.ru

Модель ARMA - это класс моделей временных рядов, сочетающий в себе процесс скользящего среднего и авторегрессионный процесс.

Модель ARMA

Модель авторегрессии и скользящей средней является одной из математических моделей, используемых для анализа и прогнозирования постоянных статистических временных рядов. Модель ARMA является обобщением двух более простых моделей временных рядов - авторегрессионной модели и модели со скользящим средним.

Рассматриваемая модель основана на предположении, что текущее значение исследуемого временного ряда полностью зависит от линейной комбинации прошлой эволюции временного ряда и белого шума. Модель ARMA может быть представлена следующим образом:

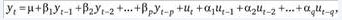
Рисунок 1: Формула. 

В данном случае.

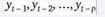
Рисунок 2: Формула. 

и

Рисунок 3 Формула. 

- Это значения задержек и белого шума.

Процесс ARMA представляет собой комбинацию процессов AR и MA. Соответственно, характеристики и свойства процесса ARMA представляют собой сочетание характеристик и свойств двух вовлеченных процессов.

При условии нулевого среднего ARMA может быть представлена как

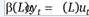
Рисунок 4: Формула. 

Если имеется обратный оператор, то ARMA имеет форму:

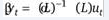
Рисунок 5. Формула. 

Если добавить к классическим ARMA-моделям некоторые экзогенные факторы x, то получим ARMAX-модели. В целом, модель содержит как текущие значения факторов, так и запаздывающие значения. Такие модели называются ARMAX(p,q,k), где k - число лагов экзогенных факторов.

Перечислим свойства автокорреляционной и частичной автокорреляционной функции процессов AR, MA, ARMA:

Автокорреляционная функция убывает экспоненциально, где число ненулевых лагов парциальной автокорреляционной функции равно степени авторегрессионного процесса;
Функция авторегрессии частичной скользящей средней имеет отрицательный наклон, а количество ненулевых лагов равно степени процесса скользящего среднего.

Временные ряды и отставания в экономических моделях

Для анализа большинства экономических показателей требуются годовые, квартальные, месячные и ежедневные данные. Для этого данные должны быть упорядочены в соответствии с тем, когда они были собраны, т.е. должен быть сформирован временной ряд.

Различают авторегрессионные модели и модели с распределенным лагом.

Переменные с запаздыванием - это переменные, влияние которых проявляется с определенным запаздыванием. Эти модели содержат только независимые переменные в виде лагов.

Авторегрессионные модели - это модели, в которых уравнения принимают значения зависимых переменных как запаздывающие объясняющие переменные.

Отставания в экономике возникают по разным причинам, самыми важными из которых являются:

• Психологические причины, которые проявляются в вялом поведении людей. Например, люди тратят свой доход не сразу, а постепенно. Привычка вести определенный образ жизни приводит к тому, что человек приобретает одни и те же товары в течение определенного периода времени, даже если реальные доходы уменьшаются.
• Технологические причины. Примером может служить изобретение персонального компьютера, после которого мейнфреймы не были сразу же вытеснены из-за необходимости замены программного обеспечения.
• Институциональные причины. Примерами являются контракты между компаниями, трудовые договоры, которые требуют определенного постоянства на определенный период времени.
• Особенности формирования показателей в экономике. Например, инфляция в большинстве случаев является инерционным процессом, а денежный мультипликатор проявляется и в определенное время.