Анализ переходных и установившихся процессов методом интеграла свертки

Содержание:

Анализ переходных и установившихся процессов методом интеграла свертки:

Интеграл Дюамеля применяют для расчета токов, напряжений переходных режимов в схеме с нулевыми начальными условиями, если воздействие имеет сложную форму. В табл. 7.1 приведены формы записи интеграла Дюамеля.

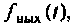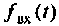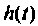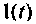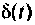При определении тока или напряжения переходного режима, обозначенных можно использовать одну из восьми форм записи, расчет по которой проще. В интеграл Дюамеля кроме входного сигнала входят временные характеристики: переходная функция (характеристика) h(t) и импульсная переходная функция (характеристика) . Временные характеристики — это реакция цепи на типовые воздействия иди при нулевых начальных условиях в схеме.

Временные характеристики бывают переходные 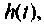если входное воздействие представлено в виде  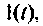и импульсные  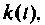если воздействие имеет вид 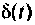-функции. Переходная характеристика определяется как

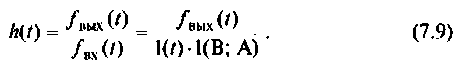
Из выражения (7.9) следует, что переходная характеристика равна току 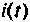или напряжению u(t) переходного режима при подключении цепи к источнику ЭДС с 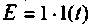В или источнику тока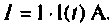

Импульсная характеристика 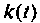определяется из соотношения

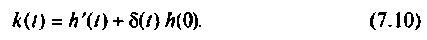
В табл. 7.2 приведены графики типовых воздействий и разновидностей временных характеристик.

Методы определения переходных и импульсных характеристик

Классический метод построения переходных и импульсных характеристик:

Для расчета переходных характеристик классическим методом:

1. на вход цепи полают единичное ступенчатое воздействие напряжения (тока)
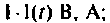
2. записывают формулу для определения h(t) используя соотношение 
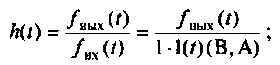
3. находят классическим методом 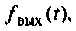т.е. ток или напряжение переходного режима в зависимости от разновидности определяемой характеристики;
4. рассчитывают 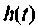и строят график;
5. проверяют расчет для 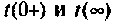по схеме и сравнивают с аналитическим выражением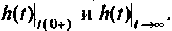    

Для расчета импульсных характеристик пользуются соотношением (7.10), связывающим переходные и импульсные характеристики

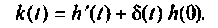
Пример расчета переходных и импульсных характеристик классическим методом

Для дифференцирующего RС-контура (рис. 7.1) определить переходную и импульсную характеристики по напряжению на сопротивлении R2.

На вход цепи, изображенной на рис.7.2. подают единичное ступенчатое напряжение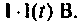

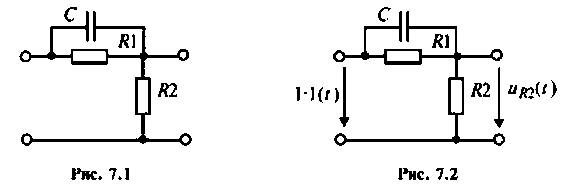
Записывают формулу для определения h(t), используя соотношение (7.9) и табл. 7.2

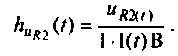
Определяют классическим методом напряжение переходного режима на сопротивлении R2:

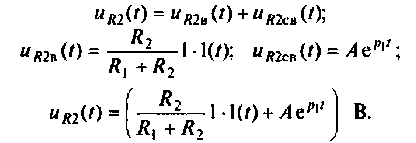
Начальное значение А определяют по выражению

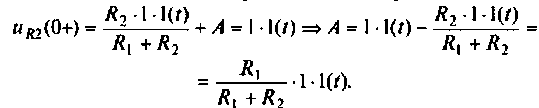
Корен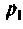, определяют как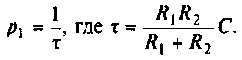

Напряжение переходного режима на сопротивлении 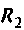будет иметь вид

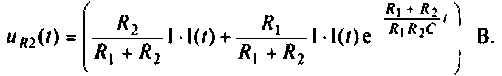
Определяют переходную характеристику по напряжению

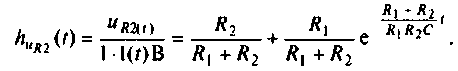
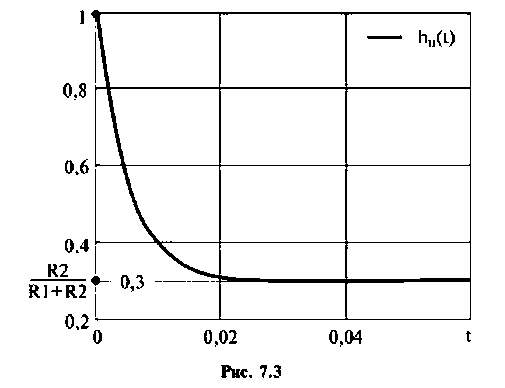
График переходной характеристики по напряжению 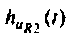приведен на рис. 7.3.

Определяют импульсную характеристику по связи (7.10) с переходной

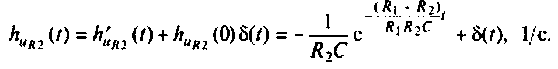
Размерность импульсной характеристики (1/с), а физически характеризует скорость изменения переходной характеристики.

Построение переходных и импульсных характеристик операторным методом

Для расчета переходных и импульсных характеристик операторным методом:

1)для заданной электрической цени и операторной форме составляют уравнения входа и выхода, например для 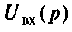и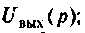 

2) определяют выражение для передаточной функции электрической цепи

3) определяют с помощью обратного преобразования Лапласа импульсную характеристику

4) получают изображение переходной характеристики по полученной передаточной функции

5) определяют переходную характеристику по полученному изображению переходной функции с помощью обратного преобразования Лапласа

Пример расчета переходных и импульсных характеристик операторным методом. Для дифференцирующего RС-контура (см. рис.7.1) определить переходную и импульсную характеристики по напряжению на сопротивлении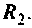

Для определения передаточной функции контура составим уравнения напряжения этого контура в операционной форме

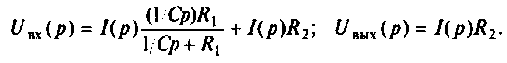
Из второго уравнения находим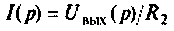 и, подставляя в первое уравнение, получаем

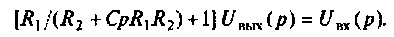
После преобразования

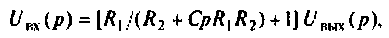
откуда передаточная функция контура

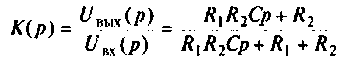
или

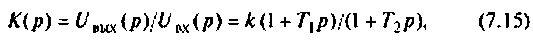
где 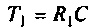— постоянная времени контура по производной; 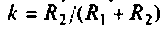— коэффициент усиления контура по сигнальной составляющей; 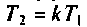— постоянная времени отставания. Поскольку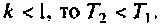

Из формулы (7.15) можно определить изображение переходной функции контура 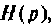подставив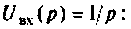

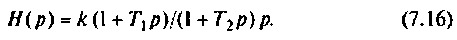
Методы определения импульсной (7.12) и переходной характеристик (7.14) электрических цепей и систем автоматического управления с помощью обратного преобразования хорошо известны и широко применяются в инженерной практике [4, 6, 14], поэтому не будем на них подробно останавливаться, а получим временные характеристики с помощью программной среды Mathcad.

Применим стандартную функцию invlaplace в среде Mathcad.

Импульсная характеристика 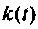определяетcя по выражению

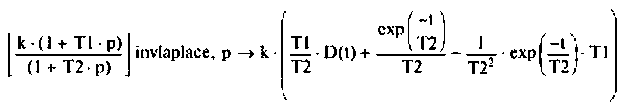
Переходная характеристика h(t) — по выражению

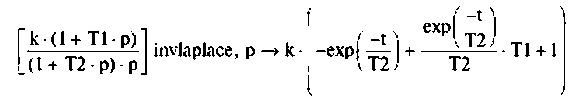
Порядок расчета переходных процессов методом интеграла Дюамеля

1. Записывают одну из восьми форм интеграла Дюамеля, приведенных и табл. 7.1.
2. Определяют соответствующую временную характеристику.
3. Вычисляют компоненты, входящие в интеграл Дюамеля.
4. Производят интегрирование и находят искомую функцию.
5. Проверяют расчет для 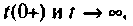 строят график найденной характеристики.

Для построения выходных переменных воспользуемся интегралом свертки в форме записи (7.6) и средой Mathcad:

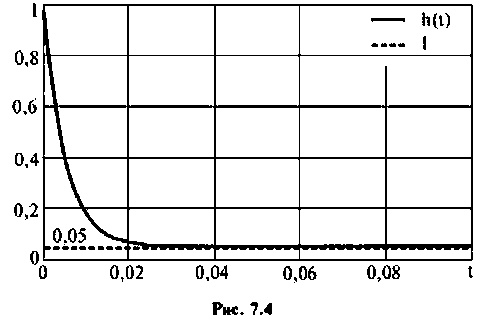
1. выходная (переходная) функция электрической цепи приведена на рис. 7.4;
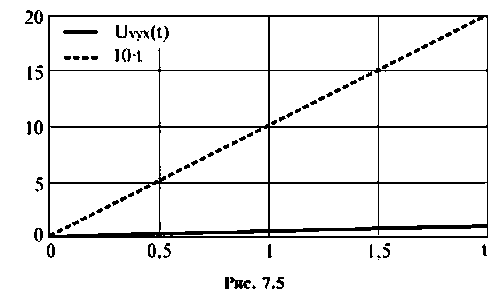
2. реакция электрической цепи на линейное воздействие 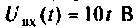 показана на рис. 7.5.

По виду входной и выходной величин осуществляется оценка свойств электрической цепи, исследуется влияние изменения параметров цепи на характер процессов, протекающих в ней.

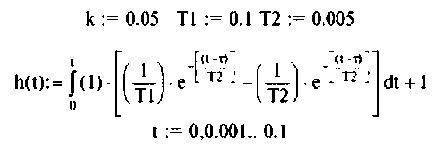
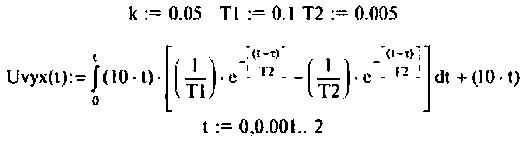
Примеры решения задач

Пример 7.4.1.

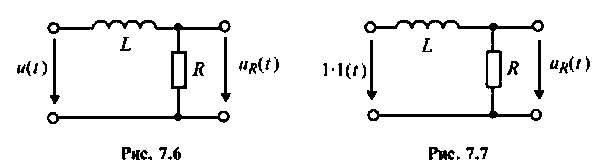
Определить напряжение на сопротивлении R интегрирующей RL-цепи (рис. 7.6). если напряжение на входе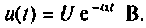

Решение

Выбирают аналитическое выражение интеграла Дюамеля из табл. 7.1

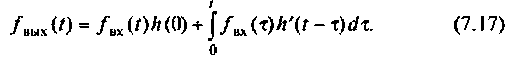
Конкретизируя величины, входящие в интеграл Дюамеля, получают

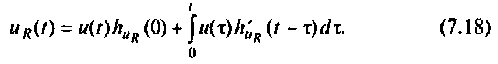
Определяют переходную характеристику но напряжению на сопротивлении R как

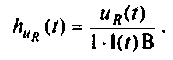
На рис. 7.7 приведена схема для расчета переходной характеристики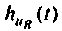

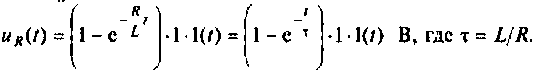
Следовательно,

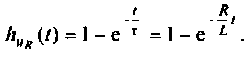
Вычисляют компоненты, входящие в интеграл Дюамеля:

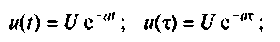
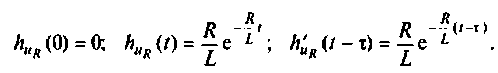
Производя интегрирование в соответствии с выражением (7.10), находят искомое напряжение

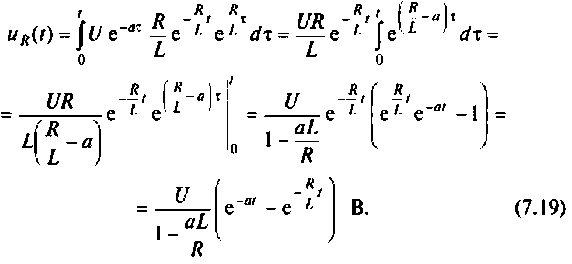
Проверяют расчет для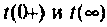

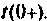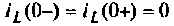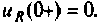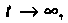На рис. 7.К приведена эквивалентная схема для На основании первого закона коммутации индуктивность заменяют разрывом. Следовательно,  Если  то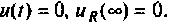

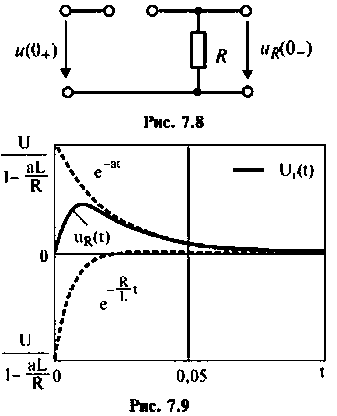
Подставляя 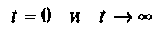в аналитическое выражение, получают такие же значения. На рис. 7.9 приведен график  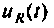при 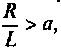построенный по выражению (7.19) и среде Mathcad, где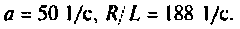 

Пример 7.4.2.

Определить напряжение на сопротивлении R и интегрирующей /fi-цеии (рис. 7.7), если напряжение па входе 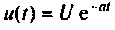. Аналитические преобразования, расчеты и построение графиков выполнить в среде Mathcad.

Дано: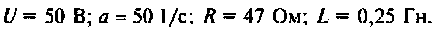

Решение

Определение напряжения 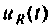проведем с помощью интеграла Дюамеля, как и в примере 7.4.1.

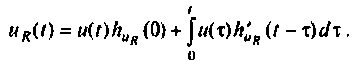
В этом выражении составляющая 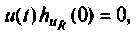тогда

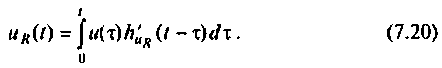
Определим подынтегральную функцию, для этого воспользуемся выражениями 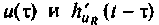из примера 7.4.1. В среде Mathcad интеграл (7.20) и результат его символического вычисления принимают вид

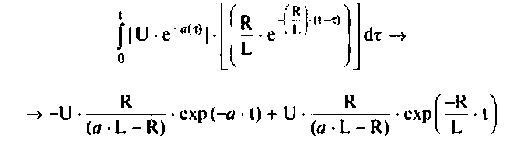
Программа для вычисления и построения входного и выходного напряжения имеет следующий вид

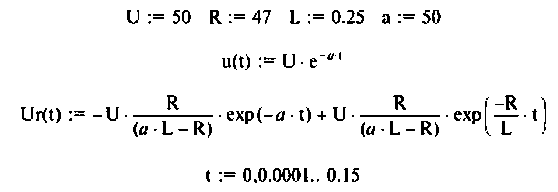
Графическое изображение входного и выходного напряжений показано на рис. 7.10.

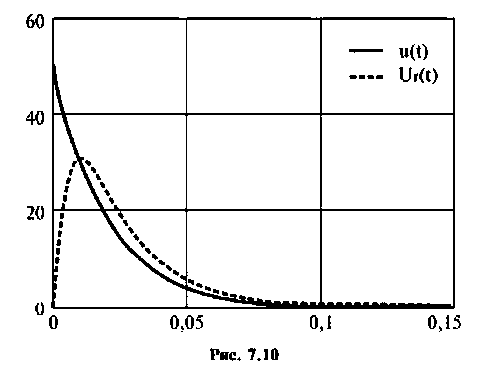
Пример 7.4.3.

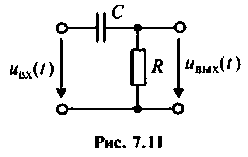
Для повышения разрешающей способности PЛC применяют дифференцирование сигналов. Рассчитать напряжение на выходе RС-цепи, поступающее на вход преобразовательного устройства РЛС, если на входе цепи (рис. 7.11) появляется прямоугольный видеоимпульс с параметрами 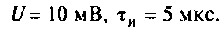Параметры RС-цепи: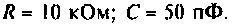

Решение

Определяют переходную характеристику по напряжению

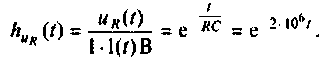
Входной и выходной сигналы методом наложения представляют в виде суммы ступенчатых воздействий (рис. 7.12). Входной сигнал определяют из соотношения

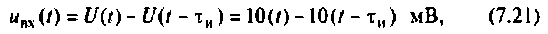
а выходной

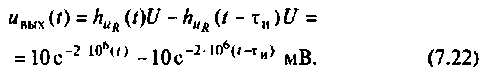
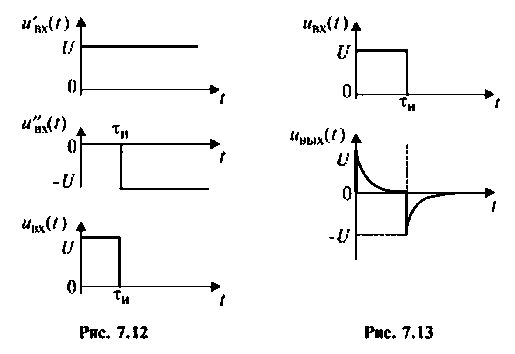
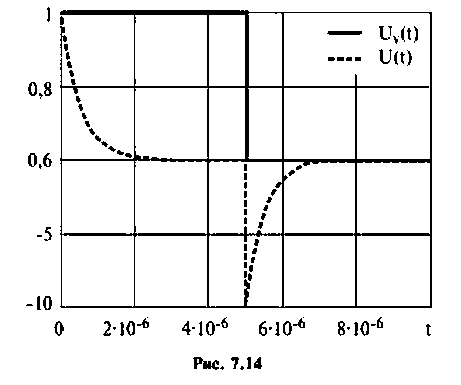
Приближенно графики входного и выходного напряжений изображены на рис. 7.13.

В математической среде Mathcad решение этой задачи упрощается и может быть представлено следующими программами:

1)  для моделирования входного импульсного напряжения

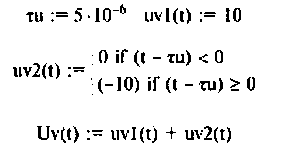
2)  для моделирования выходного напряжения

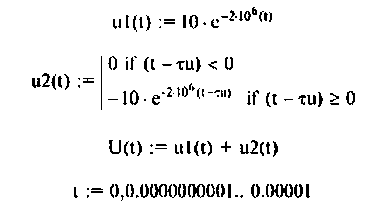
Графики напряжений приведены па рис. 7.14.