
Аналитическая статика в теоретической механике
Содержание:
Аналитическая статика:
До сих пор мы рассматривали движение материальной точки. Все положения, изложенные нами для случая движения одной материальной точки, применимы целиком к твердому телу, движущемуся поступательно, или к телу, размерами которого по условию задачи можно пренебречь и считать его за материальную точку. Если же система материальных точек перемещается как угодно в пространстве, то для изучения движения системы необходимо изучить движение каждой ее точки отдельно.
Общие теоремы динамики системы
Перейдем теперь, к изложению общих теорем динамики системы. Динамика системы изучает движение материальных точек под действием сил. Все силы, действующие на точки материальной системы, можно разделить на внешние и внутренние. Внутренними называются силы взаимодействия между отдельными точками материальной системы; внешние же силы — это те, которые приложены извне к рассматриваемой нами системе. Такое разделение сил является условным и зависит от того, что принято нами за систему. Так, например, сила тяжести по отношению к рассматриваемому нами телу, является внешней силой; если же в состав системы включить и земной шар, то силу тяжести, являющуюся воздействием на тело Земли, следует отнести уже к силам внутренним.
Силы, действующие на отдельные точки системы, как мы увидим ниже, можно разграничить по другому признаку.
Движение большинства систем ограничено связями. Такие системы в отличие от систем свободных называются несвободными.
Связи, стесняя свободу движения системы, накладывают на движение ее точек определенные ограничения. Эти ограничения выражаются в форме уравнений связей, причем эти уравнения могут содержать, помимо координат точек системы, еще время и скорости. Связи, уравнения которых содержат координаты точек и время, называются голономными. Система, подчиненная голономным связям, называется голономной системой. Если же уравнения связей, кроме координат точки и времени, содержат также и скорости их, то такие связи называются неголономными, системы же, подчиненные таким связям,— неголономными системами.
Голономные связи
Голономные связи, уравнения которых содержат только координаты точек, называются стационарными. Если же в уравнения голономных связей, помимо координат точек, входит еще и время, то такие связи, изменяющиеся во времени, называются нестационарными.
Обозначим число точек материальной системы через 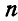
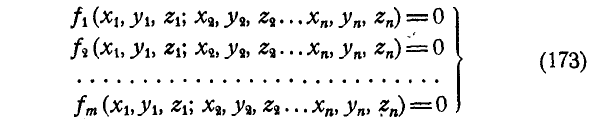
Уравнения нестационарных связей, содержащие еще и время t, могут быть в общем виде записаны так:
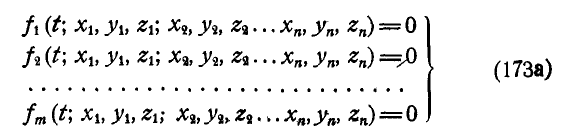
Рассмотрим несколько примеров составления уравнений стационарных связей.
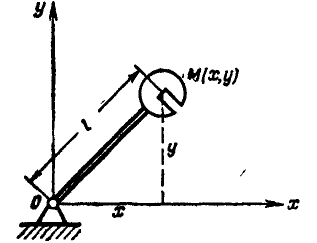
Рис. 287.
Нож М копра для испытания материалов на ударную нагрузку, скрепленный жестко со стержнем ОМ (рис. 287), может двигаться только по окружности радиуса 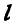 с центром в точке О; поэтому уравнение связи точки М будет:
с центром в точке О; поэтому уравнение связи точки М будет: 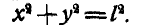
Рис. 288.
Аналогично могут быть составлены уравнения связей кривошипно-шатунного механизма (рис. 288):
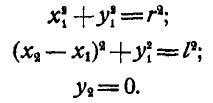
Для шарнирного четырехзвенника (рис. 289) уравнения связей примут вид:
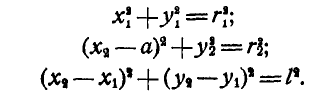
Рис. 289.
В качестве еще одного примера рассмотрим центробежный регулятор (рис. 290), состоящий из двух одинаковых грузов 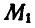 и
и  , могущих вместе с рукоятками
, могущих вместе с рукоятками 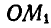 и
и 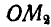 отклоняться на угол
отклоняться на угол 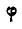 от вертикальной оси и поворачиваться на угол
от вертикальной оси и поворачиваться на угол 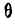 вокруг нее.
вокруг нее.
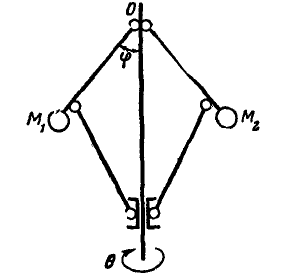
Рис. 290.
Таким образом, движение грузов  и
и  может происходить по сфере радиуса
может происходить по сфере радиуса  ; поэтому уравнение связей регулятора принимает вид:
; поэтому уравнение связей регулятора принимает вид:
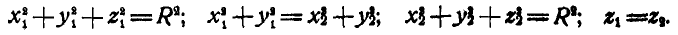
Приведем пример нестационарной связи.
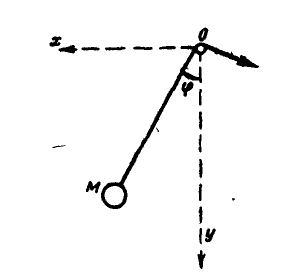
Рис. 291.
Пусть имеется грузнк М, прикрепленный к нити, проходящей через неподвижное кольцо О (рис. 291). Если во время качания грузика М в плоскости чертежа нить постепенно втягивать сквозь кольцо так, чтобы длина ОМ являлась функцией времени, то мы получаем математический маятник переменной длины 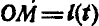 . Грузик М будет описывать окружность переменного радиуса:
. Грузик М будет описывать окружность переменного радиуса:
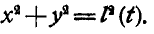
Два типа связи
По характеру ограничений, налагаемых связями на движения точек системы, связи разделяются на два типа:
- Удерживающие, или двусторонние связи, которые, препятствуя перемещению точек системы в каких-либо направлениях, одновременно препятствуют перемещениям в направлениях, прямо противоположных первым, например шарнирные соединения, поршень, движущийся в цилиндре, и пр.
- Неудерживающие, или односторонние связи, которые, препятствуя каким-либо перемещениям, не препятствуют перемещениям, прямо противоположным. Это мы наблюдаем, например, при перемещении тела по поддерживающей его горизонтальной плоскости. Здесь тело не может перемещаться вертикально вниз; в направлении же, прямо противоположном (по вертикали вверх), оно перемещаться может. Если тело накрыть сверху второй плоскостью, как это было принято для ползуна
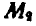 (рис. 288), то здесь имеются уже две направляющие и связь односторонняя превращается в двустороннюю.
(рис. 288), то здесь имеются уже две направляющие и связь односторонняя превращается в двустороннюю.
Мы уже видели, что несвободная система, подчиненная связям, не в состоянии совершать любые перемещения. Перемещения эти зависят от вида и характера связей.
Возможными, или виртуальными, перемещениями называются такие бесконечно малые перемещения, которые допускаются связями в данный момент. Так, в рассмотренных выше примерах возможным перемещением стержня ОM копра (рис. 287) является поворот стержня на некоторый бесконечно малый угол вокруг оси О. Возможным перемещением шарнирного четырехзвенника (рис. 289) является поворот кривошипа 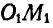 на некоторый угол и вследствие этого соответствующий поворот звена
на некоторый угол и вследствие этого соответствующий поворот звена 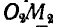 и смещение звена
и смещение звена 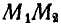 и т. д.
и т. д.
Так как величины возможных перемещений предполагаются бесконечно малыми, то направления их можно считать совпадающими с направлениями касательных к траекториям.
Не следует, однако, смешивать перемещения возможные с действительными. При движении системы из всех ее возможных перемещений (их может быть много) имеется одно действительное перемещение, обусловленное не только характером связей, но действующими силами и начальными условиями.
Чтобы отличать возможные бесконечно малые перемещения (виртуальные отклонения) от действительных, условились возможные перемещения обозначать: 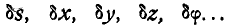 , а действительные через
, а действительные через 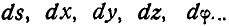 . Посмотрим теперь, какие ограничения накладывают связи на систему.
. Посмотрим теперь, какие ограничения накладывают связи на систему.
Пусть система состоит из 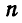 материальных точек. При условии, что все точки системы свободны, мы имели бы
материальных точек. При условии, что все точки системы свободны, мы имели бы 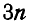 произвольных перемещений:
произвольных перемещений: 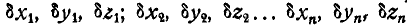 .
.
Если система подчинена 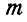 стационарным связям (173), то, взяв полные дифференциалы от уравнений связей, получим
стационарным связям (173), то, взяв полные дифференциалы от уравнений связей, получим  ограничений, которым должны удовлетворять указанные выше перемещения:
ограничений, которым должны удовлетворять указанные выше перемещения:
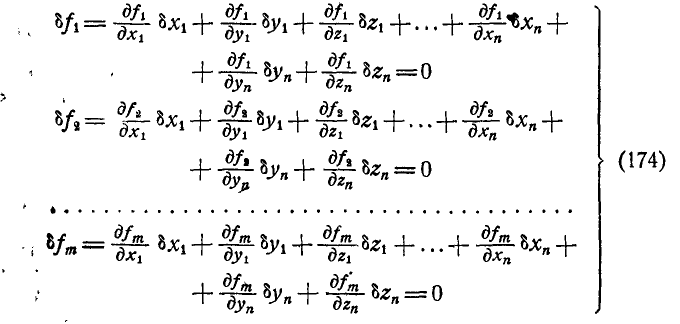
Отсюда следует, что произвольными уже остаются  перемещений. Заданием
перемещений. Заданием 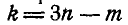 независимых величин вполне определяется положение всех точек системы, поэтому говорят, что система имеет
независимых величин вполне определяется положение всех точек системы, поэтому говорят, что система имеет 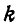 степеней свободы.
степеней свободы.
Так, положение точки в пространстве определяемся тремя координатами, а поэтому свободная точка обладает тремя степенями свободы. Если мы ограничим движение точки тем, что заставим ее двигаться по поверхности, как это имеет место, например, для каждого из грузов 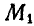 или
или 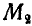 центробежного регулятора (рис. 290), то условия, которым должны удовлетвврять перемещения
центробежного регулятора (рис. 290), то условия, которым должны удовлетвврять перемещения 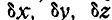 каждого из грузов, получатся путем составления полного дифференциала от уравнений связей:
каждого из грузов, получатся путем составления полного дифференциала от уравнений связей:
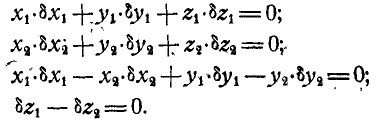
Эта система состоит из двух материальных точек  и
и  подчиненных четырем уравнениям связей. Следовательно, она обладает 6 — 4 = 2, т. е. двумя степенями свободы, так как каждая свободная точка имеет три степени свободы. Отсюда число независимых возможных перемещений будет два (регулятор имеет две степени свободы).
подчиненных четырем уравнениям связей. Следовательно, она обладает 6 — 4 = 2, т. е. двумя степенями свободы, так как каждая свободная точка имеет три степени свободы. Отсюда число независимых возможных перемещений будет два (регулятор имеет две степени свободы).
Следует отметить, что число степеней свободы всегда равно числу кинематических уравнений движения, которыми определится положение материальных точек. Так, например, тело, вращающееся вокруг неподвижной точки, имеет три степени свободы; тело, движущееся как угодно в. пространстве — шесть степеней свободы и пр.
Если система подчинена связям нестационарным, то в этом случае, как было указано выше, под возможным перемещением системы понимают перемещение по связям, мгновенно остановившимся в данный момент. В этом случае, полагая 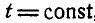 , мы получим для нестационарных связей из уравнений(173 а) такие же ограничения перемещений (174), какие имеют место и при стационарных связях. Не то будет с действительными перемещениями. Если для случая стационарных связей действительные перемещения рассматривают как частные случаи возможных [так как вид ограничений для возможных перемещений и действительных будет один и тот же, выраженный формулами (174)], то для случая нестационарных связей в выражения ограничений (174), налагаемых связями на действительные перемещения, войдут дополнительно слагаемые
, мы получим для нестационарных связей из уравнений(173 а) такие же ограничения перемещений (174), какие имеют место и при стационарных связях. Не то будет с действительными перемещениями. Если для случая стационарных связей действительные перемещения рассматривают как частные случаи возможных [так как вид ограничений для возможных перемещений и действительных будет один и тот же, выраженный формулами (174)], то для случая нестационарных связей в выражения ограничений (174), налагаемых связями на действительные перемещения, войдут дополнительно слагаемые 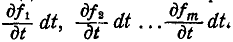 Поэтому для случая нестационарных связей действительные перемещения точек системы хотя и могут быть определены, но они уже не находятся в числе возможных перемещений. Мы уже знаем, что связи, ограничивая свободу перемещений системы, изменяют характер ее движения; при этом точки системы при наличии связей, получают в результате действующих на них сил ускорения, отличные от тфс, какие они получили бы при действии тех же сил, будучи свободными.
Поэтому для случая нестационарных связей действительные перемещения точек системы хотя и могут быть определены, но они уже не находятся в числе возможных перемещений. Мы уже знаем, что связи, ограничивая свободу перемещений системы, изменяют характер ее движения; при этом точки системы при наличии связей, получают в результате действующих на них сил ускорения, отличные от тфс, какие они получили бы при действии тех же сил, будучи свободными.
Таким образом, эффект действия связей проявляется в форме изменения ускорения; следовательно, это изменение равносильно действию некоторых сил.
Отсюда эффект действия связей может быть представлен так же, как и в статике, действием сил, которые называются реакциями связей.
Реакции связей не могут быть определены до тех пор, пока не исследовано движение.
Из сказанного следует, что силы, действующие на точки системы, могут быть разделены по другому признаку, а именно на силы задаваемые и реакции связей.
Если разграничение сил на внешние и внутренние является условным, то разделение сил по второму признаку на задаваемые и реакции связей уже не является условным.
Пусть материальная точка движется по гладкой поверхности; так как реакция связи все время направлена нормально к поверхности, то работа ее на любом возможном перемещении точки, очевидно, равна нулю. Можно было бы привести большое число примеров, когда при отсутствии трения работа реакций связей на возможных перемещениях точек системы обращается в нуль. Мы рассматриваем связи без трения, так как работа сил трения мала не сравнению с работой других приложенных сил. Если же мы хотим учесть cute и силы трения, то таковые будем относить к силам задаваемым. Правда, работа отдельных реакций на возможных перемещениях точек в отдельных случаях может и не обращаться в нуль.
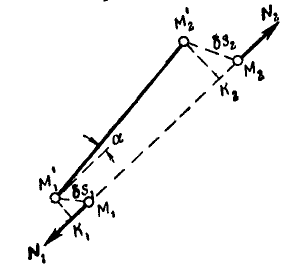
Рис. 292.
В качестве примера такого рода связи рассмотрим систему, состоящую из двух материальных точек  и
и 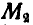 (рис. 292), связанных между собой стержнем неизменяемой длины. Реакции
(рис. 292), связанных между собой стержнем неизменяемой длины. Реакции 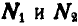 стержня, приложенные к материальным точкам
стержня, приложенные к материальным точкам 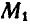 и
и 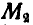 , равны по величине и направлены по оси стержня в противоположные стороны. Дадим системе возможное перемещение и подсчитаем при этом перемещении сумму работ
, равны по величине и направлены по оси стержня в противоположные стороны. Дадим системе возможное перемещение и подсчитаем при этом перемещении сумму работ 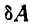 реакций
реакций 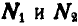 :
:
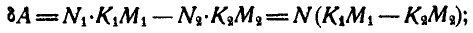
но так как
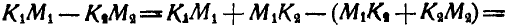
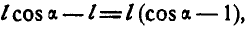
то
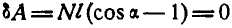 .
.
Так как при 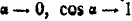 .
.
Отсюда видно, что хотя элементарная работа каждой реакции на возможном перемещении не равна нулю, но сумма работ этих реакций обращается в нуль.
Свази называются идеальными, если сумма работ реакций связей на любом возможном перемещении системы равна нулю.
Аналитическое условие идеальности связей может быть выражено:
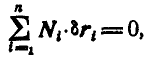
или
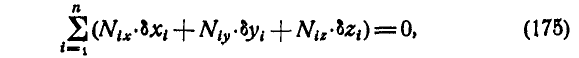
где 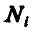 — равнодействующая реакций связей в
— равнодействующая реакций связей в 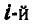 точке системы.
точке системы.
Принцип возможных перемещений
Перейдем теперь к изложению самого общего условия равновесия систем, называемого принципом возможных, или виртуальных, перемещений.
Пусть система, состоящая из 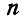 материальных точек
материальных точек 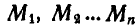 , подчинена идеальным двусторонним связям и находится в равновесии (рис. 293).
, подчинена идеальным двусторонним связям и находится в равновесии (рис. 293).
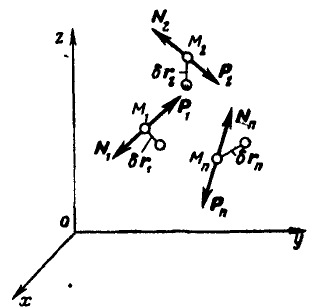
Рис. 293.
Обозначим равнодействующие всех задаваемых сил, приложенных к точкам 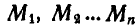 , через
, через 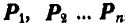 , а реакции связей в этих точках — через
, а реакции связей в этих точках — через 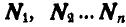 .
.
Условия равновесия отдельных точек системы будут:
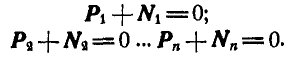
Дадим теперь нашей системе мысленно возможное перемещение; тогда, обозначая векторы возможных перемещений точек 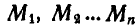 соответственно через
соответственно через 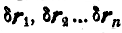 , можем написать:
, можем написать:
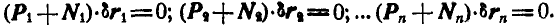
Складывая почленно эти равенства, найдем:
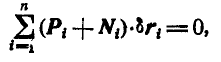
или
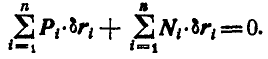
Но так как по условию связи идеальные, то работа реакций связей обращается в нуль, т. е.:
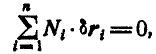
откуда
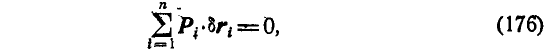
или
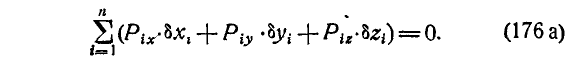
Это и есть условие равновесия для задаваемых сил, приложенных к системе.
Последнее уравнение (176 а) выражает принцип, возможных перемещений в форме Лагранжа.
Докажем достаточность этого условия для равновесия. Положим, что условие (176) выполнено, а система не находится в равновесии. В таком случае под действием задаваемых сил и реакций связей система придет в движение и совершит за малый промежуток времени действительное перемещение. Так как при этом для точек системы получится положительное приращение кинетической энергии, то и силы, приложенные к точкам системы, совершат положительную работу; поэтому:
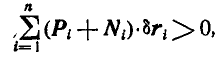
или
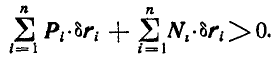
Но в силу идеальности связей:
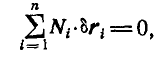
откуда
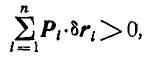
что противоречит принятому нами положению (176).
Итак, условие, необходимое и достаточное для равновесия всякой системы, подчиненной идеальным двусторонним связям, состоит в том, что при всяком бесконечно малом возможном перемещении системы из рассматриваемого положения равновесия сумма элементарных работ всех задаваемых сил, приложенных к точкам системы, должна быть равна нулю.
Ценность принципа возможных перемещений заключается в том, что работа реакций связей в уравнения (176) и (176 а) не входит.
Этот принцип, выражающий условие равновесия системы, является настолько общим, что из него может быть выведена любая теорема статики, как следствие.
Выведем, например, уравнения равновесия сил  , приложенных к свободной материальной точке М (рис. 294).
, приложенных к свободной материальной точке М (рис. 294).
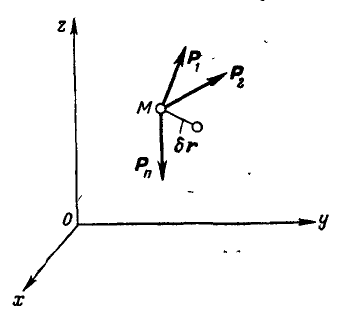
Рис. 294,
Дадим точке М любое возможное перемещение 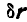 ; тогда по уравнению (176) находим:
; тогда по уравнению (176) находим:
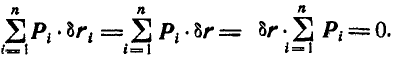
Величину 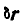 выносим за знак суммы, как одинаковый множитель для всех сил.
выносим за знак суммы, как одинаковый множитель для всех сил.
Так как 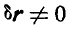 , то
, то 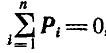 , откуда
, откуда 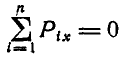 ;
; 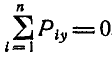 ;
; 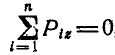 , что и выражает уравнения равновесия.
, что и выражает уравнения равновесия.
Применение принципа возможных перемещений выясним на отдельных задачах.
Задача №1
В точке В наклонной плоскости АВ устроен неподвижный блок, через который перекинута гибкая нить, прикрепленная своими концами к двум грузам Р и Q (рис. 295). Пренебрегая массой блока и трением, найти величину угла 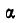 при равновесии.
при равновесии.
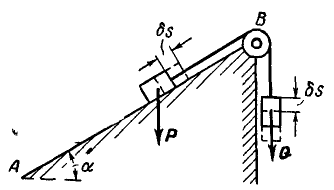
Рис. 295.
Решение. Дадим мысленно системе, состоящей из двух грузов Р и Q, возможное перемещение, для чего груз Q опустим вниз на величину 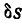 , тогда груз Р передвинется по плоскости вверх также на
, тогда груз Р передвинется по плоскости вверх также на 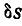 (можно было бы это перемещение произвести в обратную сторону). Применяя уравнение работ (176), составим сумму работ заданных сил Р и Q на указанных перемещениях и приравняем эту работу нулю. Вспоминая определение элементарной работы силы, можем написать:
(можно было бы это перемещение произвести в обратную сторону). Применяя уравнение работ (176), составим сумму работ заданных сил Р и Q на указанных перемещениях и приравняем эту работу нулю. Вспоминая определение элементарной работы силы, можем написать:
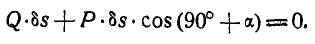
Сократим все уравнение на 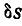 и заменим
и заменим 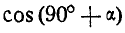 через
через 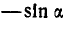 , после чего найдем:
, после чего найдем:
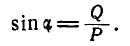
Задача №2
Простой рычажный пресс состоит из соединенных между собой шарнирно стержней АВ и ВС, DE и EF, одинаковой длины 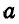 каждый (рис. 296). Стержни соединены с поднимающейся горизонтальной платформой MN, на которую кладется прессуемое тело, .причем прессование происходит при сближении точек В и Е. Найти соотношение между приложенными силами Р и силой Q, давящей на тело при равновесии.
каждый (рис. 296). Стержни соединены с поднимающейся горизонтальной платформой MN, на которую кладется прессуемое тело, .причем прессование происходит при сближении точек В и Е. Найти соотношение между приложенными силами Р и силой Q, давящей на тело при равновесии.
Рис. 296.
Решение. При решении этой задачи удобнее всего воспользоваться принципом возможных перемещений, выраженным в форме (176 а).
Проведем координатные оси. Ось у направим вверх по оси симметрии механизма, а ось х слева направо.
Все вычисления удобно представить в виде таблицы 10.
Таблица 10

Если проекция силы на ось обращается в нуль, как, например, в нашем случае получилось с проекцией каждой из сил Р на ось Оу, то соответствующую координату у и ее приращение 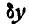 можно не находить совсем, так как при
можно не находить совсем, так как при 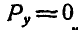 произведение
произведение 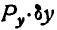 все равно обращается в нуль. В приведенной таблице ненужные нам значения
все равно обращается в нуль. В приведенной таблице ненужные нам значения 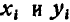 , а также
, а также 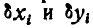 прочеркнуты.
прочеркнуты.
Составляя для каждой из заданных сил произведения 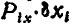 и
и 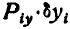 и суммируя их согласно (176 а), найдем:
и суммируя их согласно (176 а), найдем:
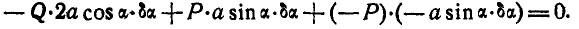
Приведем подобные члены и сократим все уравнение на 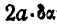 :
:
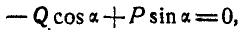
откуда
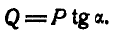
При 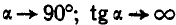 , а отсюда и
, а отсюда и  . Следовательно, при большем угле
. Следовательно, при большем угле 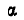 прессование происходит лучше.
прессование происходит лучше.
Задача №3
Механизм заднего колеса плуга состоит из двух рычагов: прямого АВ и ломаного CD, вращающихся вокруг неподвижных шарниров 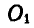 и
и 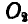 . Концы этих стержней В и С соединены шарнирно шатуном ВС, который составляет с ними в положении, показанном на чертеже, углы
. Концы этих стержней В и С соединены шарнирно шатуном ВС, который составляет с ними в положении, показанном на чертеже, углы 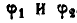 . В этом же положении механизма превышение точки А над осью О, равно h и горизонтальное расстояние между точкой D и осью
. В этом же положении механизма превышение точки А над осью О, равно h и горизонтальное расстояние между точкой D и осью 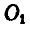 равно Н. В точке А приложена горизонтальная сила Р, в точке D — вертикальная сила
равно Н. В точке А приложена горизонтальная сила Р, в точке D — вертикальная сила 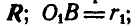
 Найти соотношение между силами Р и R, при котором механизм будет оставаться в равновесии (рис. 297).
Найти соотношение между силами Р и R, при котором механизм будет оставаться в равновесии (рис. 297).
Рис. 297.
Решение. Дадим системе возможное перемещение, показанное на рисунке 297 тонкой линией.
Ввиду малости возможных перемещений заменим перемещения точек А, В, С и D, происходящие по дугам окружностей, касательными к этим дугам. Величины возможных перемещений этих точек обозначим соответственно через 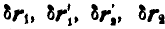 . Тогда, применяя уравнение работ в форме (176), будем иметь:
. Тогда, применяя уравнение работ в форме (176), будем иметь:
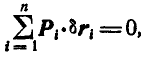
или, что то же самое:
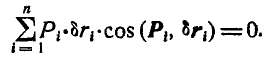
Вспоминая определение элементарной работы силы (138). получим:
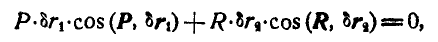
или
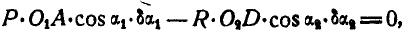
откуда
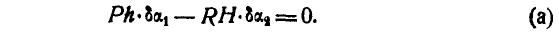
Найдем соотношение между 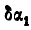 и
и 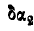 . Из чертежа имеем:
. Из чертежа имеем:
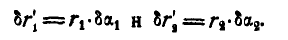
Проекции перемещений 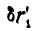 и
и 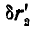 на направление шатуна ВС равны между собой, поэтому:
на направление шатуна ВС равны между собой, поэтому:
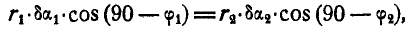
или
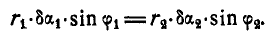
Исключая из последнего уравнения, а также из уравнения (а) 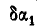 и
и 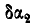 , находим окончательно:
, находим окончательно:
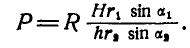
Задача №4
На балку АВ, лежащую на двух опорах А и В, действует система вертикальных сил: 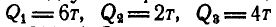 (рис. 298, а). Определить, пользуясь принципом возможных перемещений, реакцию связи в шарнире В.
(рис. 298, а). Определить, пользуясь принципом возможных перемещений, реакцию связи в шарнире В.
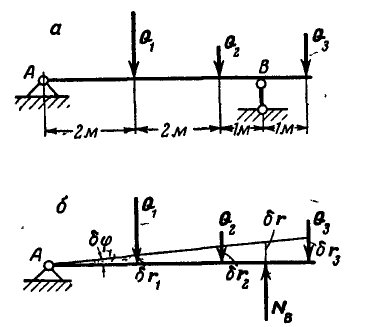
Рис. 298.
Решение. Преимущество принципа возможных перемещений перед теоремами статики заключается в том, что здесь совершенно исключаются из рассмотрения реакции связей. Однако, пользуясь принципом возможных перемещений, можно определять также и реакции связей, для чего следует мысленно уничтожить связь и взамен этого приложить ее реакцию.
Таким путем реакции связей переводятся в разряд сил задаваемых; затем задача уже решается обычным способом. Так, для определения реакции шарнира В устраним опору В и заменим ее опорной реакцией 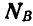 (рис. 298, б). Теперь балка получила возможность поворачиваться вокруг шарнира А. Дадим балке возможное перемещение и составим уравнение работ:
(рис. 298, б). Теперь балка получила возможность поворачиваться вокруг шарнира А. Дадим балке возможное перемещение и составим уравнение работ:
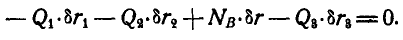
Далее имеем:
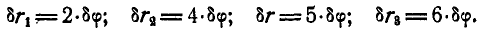
Следовательно:
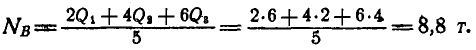
Задача №5
Определить усилия 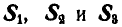 в стержнях АС, ВС и АВ треугольной формы ABC, длины сторон которой a, b и с и углы
в стержнях АС, ВС и АВ треугольной формы ABC, длины сторон которой a, b и с и углы 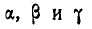 (рис. 299, а).
(рис. 299, а).
В точке С приложена вертикальная сила Р, а в точках А и В устроены неподвижно и подвижно шарнирные опоры.
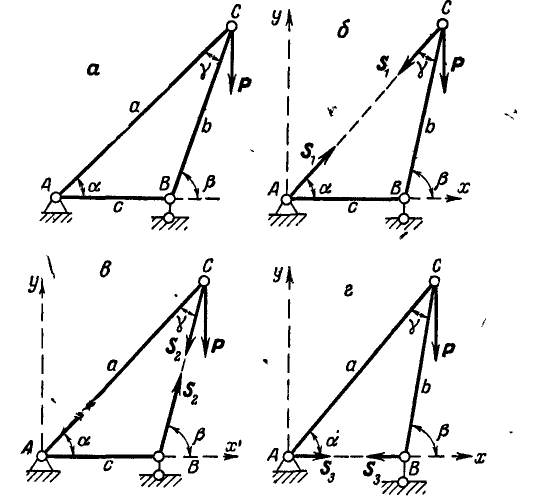
Рис. 299.
Решение. Найдем сначала усилие 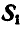 в стержне АС, для чего вырежем этот стержень и взамен него введем две реактивные силы
в стержне АС, для чего вырежем этот стержень и взамен него введем две реактивные силы 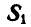 и —
и —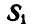 , направленные вдоль стержня АС в противоположные стороны (рис. 299, б). После такой замены силы
, направленные вдоль стержня АС в противоположные стороны (рис. 299, б). После такой замены силы 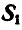 и следует уже считать заданными. При возможном перемещении системы в уравнение работ (176 а) войдет только работа сил
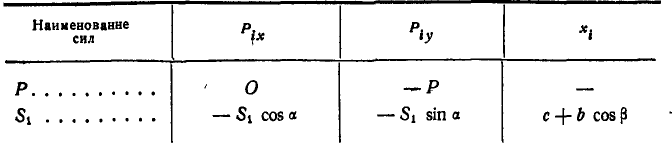
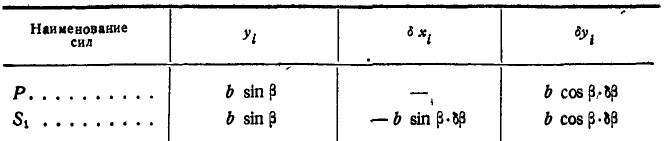
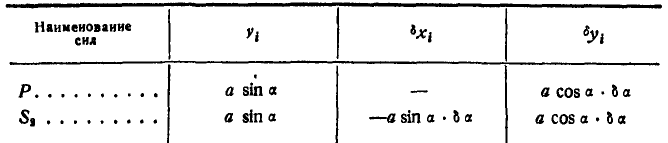
и следует уже считать заданными. При возможном перемещении системы в уравнение работ (176 а) войдет только работа сил 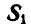 и Р, приложенных к точке С. Проведем через точку А координатные оси и все вычисления сведем в таблицу 11.
и Р, приложенных к точке С. Проведем через точку А координатные оси и все вычисления сведем в таблицу 11.
Таблица 11
После этого уравнение работ (176а) примет вид:
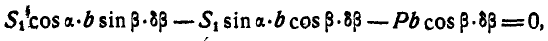
откуда
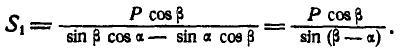
Аналогично поступаем при определении усилия в стержне ВС. Удаляем стержень и взамен него вводим реакции  и —
и — направленные вдоль стержня (рис. 299, в). Все вычисления сведем в таблицу 12.
направленные вдоль стержня (рис. 299, в). Все вычисления сведем в таблицу 12.
Таблица 12
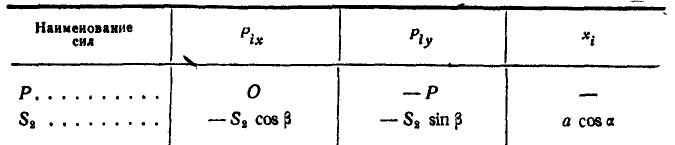
Составляем теперь уравнение работ н определяем из него искомое усилие:
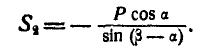
При определении усилия  в стержне АВ (рис. 299, г) уравнение работ (176а) принимает вид:
в стержне АВ (рис. 299, г) уравнение работ (176а) принимает вид:
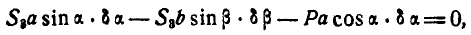
или
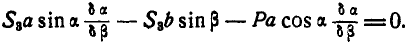
Для определения неизвестного нам отношения 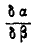 составим дополнительное уравнение. Из
составим дополнительное уравнение. Из 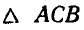 по теореме синусов находим:
по теореме синусов находим:
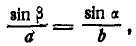
откуда
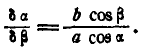
Подставляя найденное значение 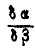 в уравнение работ, определим усилие в третьем стержне:
в уравнение работ, определим усилие в третьем стержне:
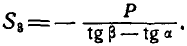
Задача №6
Каково должно быть соотношение между горизонтальными силами Р и вертикальной силой Q, приложенными к вершинам шарнирного многоугольника ABCDE, для того чтобы углы наклона стержней при равновесии были равны: 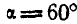 и
и 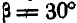 (рис. 300). Все стержни считать невесомыми и одинаковой длины:
(рис. 300). Все стержни считать невесомыми и одинаковой длины: 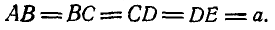
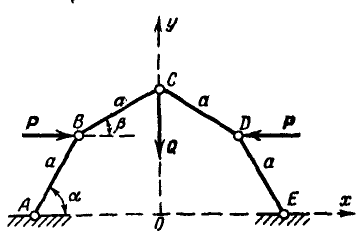
Рис. 300.
Указание: применяем уравнение работ в форме (176а), считая углы 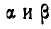 переменными:
переменными:
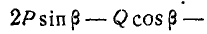
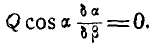
Для определения неизвестного соотношения: 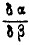 составим дополнительное уравнение, исходя из того, что при любых возможных перемещениях системы сумма проекций отрезков АВ, ВС, CD, DE на ось Ох постоянна:
составим дополнительное уравнение, исходя из того, что при любых возможных перемещениях системы сумма проекций отрезков АВ, ВС, CD, DE на ось Ох постоянна:
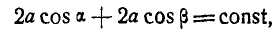
откуда
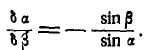
Окончательно имеем:
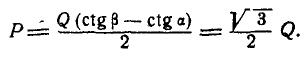
Задача №7
Два однородных стержня АВ и ВС одинаковой длины и одинакового веса Q кГ каждый скреплены между собой шарниром В. Конец А закреплен неподвижно, к концу С приложена горизонтальная сила 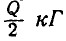 (рис. 301). Найти значение углов
(рис. 301). Найти значение углов 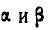 при равновесии.
при равновесии.
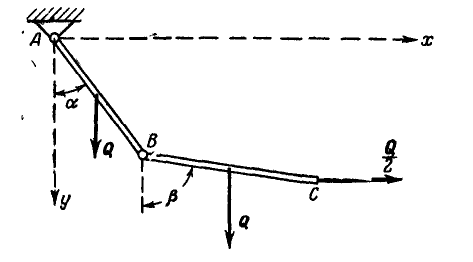
Рис. 301.
Указание: проводим через шарнир А координатные оси и применяем уравнение работ (176а). После преобразования найдем:
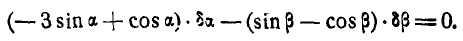
Данная система обладает двумя степенями свободы, так как ее положение определяется двумя углами 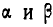 . Так как
. Так как 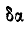 и
и 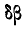 произвольны, то имеют место равенства:
произвольны, то имеют место равенства:
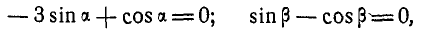
или
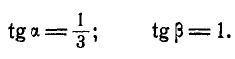
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Теорема о движении центра инерции
- Теорема количества движения
- Теорема моментов количества движения
- Теорема кинетической энергии
- Сложение движений точки
- Сложение движений твердого тела в теоретической механике - формулы и определения с примерами
- Динамика материальной точки
- Движение материальной точки