Аксиомы классической механики

Содержание:

Основные положения динамики и уравнения движения точки:

В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка. Это модель материального тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты — механические системы и сплошные тела — считают состоящими из материальных точек. Сплошное материальное тело представляют состоящим из малых по сравнению с размерами самого тела частиц, на которые мысленно разбивается тело. Каждую такую частицу считают материальной точкой.

Сила считается в механике основным, первичным понятием. Она является векторной мерой действия одного материального объекта на другой. В качестве эталона силы обычно принимают линейную силу упругости, т. е. такую меру, модуль которой при действии, например, на пружину динамометра пропорционален деформации пружины в пределах ее упругости. Свойства сил, приложенных к твердому телу и одной точке, рассматривались в статике. В динамике силы оцениваются по их динамическому действию, т. е. по изменению ими характеристик движения материальных объектов.

Движение материальных объектов всегда следует рассматривать относительно определенной системы отсчета. Оно совершается в пространстве с течением времени. В классической механике, в основу которой положены аксиомы Ньютона, пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Положение точки в таком пространстве относительно какой-либо системы отсчета определяется тремя независимыми параметрами или координатами точки. В общей теории относительности свойства пространства зависят от находящихся в нем материальных объектов и их движения. 

Время в классической механике универсально. Оно не связано с пространством и движением материальных объектов. Во всех системах отсчета, движущихся друг относительно друга, оно протекает одинаково. В теории относительности пространство и время связаны друг с другом. Они рассматриваются как единое четырехмерное пространство — время. Время при этом зависит от того, в какой системе отсчета оно рассматривается. В классической механике время определяется по какому-либо периодическому процессу, как, например, вращение Земли вокруг своей оси, колебания маятника часов и т. д.

Все положения динамики получают из ее аксиом, используя законы логики и вводя удобные для применения понятия. В основу классической механики положены аксиомы Ньютона, которые были даны в его труде «Математические начала натуральной философии», опубликованные впервые в 1687 г. Классическую механику часто называют механикой Ньютона в отличие, например, от механики теории относительности.

Для формулировки аксиом Ньютона необходимо дать определение инерциальных систем отсчета, для которых справедливы аксиомы Ньютона. Достаточно предварительно определить одну исходную или основную инерциальную систему отсчета. В дальнейшем будет показано, что инерциальных систем отсчета бесконечно много. Ньютон считал, что существует абсолютное неподвижное пространство, с которым и следует скрепить исходную инерциальную систему отсчета. Ньютоновское определение абсолютного пространства породило споры и возражения. В настоящее время целесообразно определить исходную инерциальную систему отсчета как систему осей координат, начало которой находится в центре Солнца, а оси все время направлены на одни и те же удаленные звезды. Такую систему координат называют гелиоцентрической. Ее использование в качестве инерциальной системы отсчета, как показывает опыт, не приводит к заметным погрешностям.

Основные аксиомы классической механики

Всякая система аксиом должна быть полной и независимой, т. е. отдельные аксиомы не должны, например, быть частным случаем или следовать из других аксиом. Аксиомы классической механики (или ее законы) не являются независимыми. Они не образуют и замкнутой системы, удовлетворяющей условию полноты и другим требованиям, предъявляемым к системам аксиом. Предпринималось немало попыток заменить систему аксиом Ньютона более совершенной системой, но эти попытки не были успешными. Поэтому примем за основу аксиомы Ньютона в современной их форме применительно к простейшей модели тела — материальной точке.

Первой аксиомой, или законом классической механики, является закон инерции, который был открыт еще Галилеем: материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного и прямолинейного движения относительно инерциальной системы отсчета. Материальная точка, на которую не действуют силы или действует равновесная система сил, называется изолированной материальной точкой.

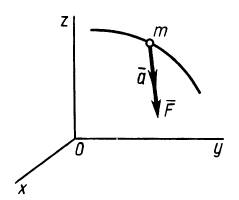
Рис. 1

Равномерное и прямолинейное движение точки называют движением по инерции. Частным случаем движения по инерции является покой точки, при котором скорость ее равна нулю. Первая аксиома содержит в себе утверждение, что простейшее материальное тело, а следовательно, и любые другие материальные тела обладают свойством инерции, т. е. свойством сохранять свое прямолинейное и равномерное движение относительно инерциальной системы отсчета. Согласно Ньютону, все материальные тела обладают врожденной способностью сопротивляться изменению своего движения по инерции. Это внутреннее свойство всех материальных тел, зависящее только от самих тел и не зависящее от присутствия в пространстве других тел. При движении материальной точки по инерции ее ускорение равно нулю. Ускорение точки, таким образом, является мерой отклонения ее движения от движения по инерции.

Вторая аксиома, или основной закон динамики, принадлежащий Ньютону, устанавливает зависимость ускорения точки относительно инерциальной системы отсчета от действующей на нее силы и массы точки: ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе (рис. 1). Если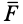 

Положительный коэффициент пропорциональности 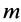, характеризующий инертные свойства материальной точки, называется инертной массой точки. Инертная масса в классической механике считается величиной постоянной, зависящей только от самой материальной точки и не зависящей от характеристик ее движения, т. е. скорости и ускорения. Масса также не зависит от природы силы, приложенной к точке. Она одна и та же для сил тяготения, сил упругости, электромагнитных сил, сил трения и других сил.

В отличие от инертной массы масса, входящая в закон тяготения Ньютона

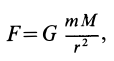
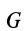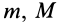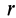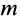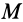называется гравитационной массой. В этом законе  — постоянная тяготения; — гравитационные массы притягивающихся точек; —расстояние между ними. Гравитационные массы  и в этом законе выполняют роль своеобразных зарядов, если сравнивать закон тяготения с законом Кулона для взаимодействия покоящихся электрических зарядов. С большой степенью точности экспериментально установлена эквивалентность инертной и гравитационной масс.

Массу обычно определяют по силе тяготения 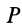 и ускорению свободного падения 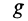у поверхности Земли. Согласно (1), в этом случае имеем

Это определение массы широко используется в механике Ньютона.

Основной закон механики является также критерием, который позволяет устанавливать, какую силу следует считать приложенной к материальной точке. Сила, приложенная к материальной точке, всегда имеет материальный источник в виде других материальных тел, которые действуют на точку путем контакта при непосредственном соприкосновении с ней или на расстоянии через посредство силовых полей. Приложенная к точке сила должна создавать у нее ускорение относительно инерциальной системы отсчета в соответствии с основным законом динамики. Только приложенная сила является причиной ускорения точки в классической механике. Это определяет наблюдателя, с точки зрения которого следует судить в механике Ньютона о взаимодействии тел, определяющих силы. Таким является наблюдатель, находящийся в инерциальной системе отсчета.

Из (1), если сила 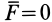, следует, что ускорение 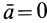, т. е. материальная точка имеет постоянную по модулю и направлению скорость относительно инерциальной системы отсчета. В основном законе содержится часть утверждения аксиомы инерции. Другая часть этой аксиомы о свойстве инерции материальной точки и всех других материальных тел в основном законе динамики не содержится.

Третья аксиома, или закон о равенстве сил действия и противодействия, определяет свойство сил взаимодействия между двумя материальными точками с точки зрения инерциального наблюдателя: силы взаимодействия двух материальных точек равны по величине и противоположны по направлению (рис. 2), т. е.

независимо от удаления точек друг от друга. Эти силы в классической механике считаются действующими вдоль одной прямой. Если не требовать этого, то и силу Лоренца, возникающую при действии одного электрического т, заряда на другой, движущийся, заряд, можно считать тоже силой взаимодействия.    

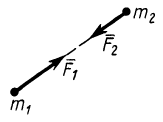
Рис. 2

Если сила действия, например 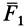, изменяется, то синхронно с ней должна, согласно (3), изменяться и сила противодействия. Это возможно для любых расстояний между взаимодействующими точками только при условии, что силовое взаимодействие распространяется мгновенно, т. е. с бесконечно большой скоростью. В действительности же все известные взаимодействия имеют конечные скорости распространения. Для устранения этой трудности взаимодействие на расстоянии целесообразно считать близкодействием, используя концепцию поля. При рассмотрении взаимодействия выделенной материальной точки с каким-либо материальным объектом на расстоянии можно считать, что точка контактно взаимодействует с полем объекта, не рассматривая в механике вопрос о передаче противодействия к источнику поля и его запаздывание из-за конечности скорости передачи.

При рассмотрении взаимодействия материальных точечных объектов с полями часто используются пробные точечные объекты, которые испытывают действие поля, но сами на поле не влияют.

Четвертая аксиома, или закон независимого действия сил (закон суперпозиции сил), не является самостоятельной аксиомой, если принять, что силы, действующие на материальную точку, складываются по правилу параллелограмма. Эта аксиома следует из аксиомы сложения сил. Закон независимого действия сил утверждает: при одновременном действии на материальную точку нескольких сил ускорение точки относительно инерциальной системы отсчета от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил. Между силами нет взаимного влияния друг на друга в создании ускорения точки^ Если к материальной точке приложена система сил 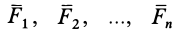, то, согласно этой аксиоме, ускорение от действия каждой из этих сил определяется по (1):

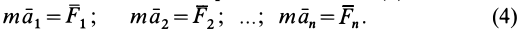
Ускорение при одновременном действии всех сил является векторной суммой ускорений, созданных отдельными силами, т. е.

Суммируя (4) и используя (5), получаем основное уравнение динамики точки:

Закон независимого действия сил следует понимать как закон суперпозиции сил, т. е. как закон сложения ускорений от действия отдельных сил. Это не означает, что приложенные к точке силы являются независимыми, особенно если среди приложенных сил есть силы реакций связей, которые всегда зависят от активных сил.

Основное уравнение динамики точки остается справедливым и для несвободной материальной точки, на которую наложены связи. Следует только в число приложенных сил включить и силы реакций связей.

Аксиомы классической механики и их следствия хорошо согласуются с результатами опытов для не очень больших скоростей движения по сравнению со скоростью света в пустоте. Для скоростей движения, сравнимых со скоростью света, следует применять механику специальной теории относительности, для которой классическая механика является ее первым приближением при малых скоростях.

• Заказать решение задач по теоретической механике

Системы единиц

Основной закон динамики (1) показывает, что единицы ускорения, массы и силы связаны между собой, а потому нельзя выбрать их независимо друг от друга. Размерность ускорения, в свою очередь, выражается через размерности длины и времени. Таким образом, единицы длины, времени, массы и силы должны определяться с учетом основного закона динамики. Независимыми из них являются только три величины. В общепринятой СИ в качестве единицы времени принята секунда (с), длины — метр (м), массы — килограмм (кг). Для них существуют эталоны. Единица силы —ньютон (Н) — является производной от указанных независимых единиц. Сила в 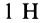равна силе, сообщающей телу массой в 1 кг ускорение, равное.

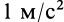Существуют и другие системы единиц, как, например, абсолютная, или 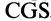 , и техническая. Абсолютная система единиц отличается от СИ тем, что в ней используются более мелкие единицы. За единицу длины принят 1 см, за единицу массы — 1 г. Тогда сила выразится в динах: ; .

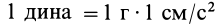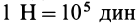В технической системе единиц в качестве независимых принимаются: для времени — секунда, длины — метр, для силы— килограмм-сила (кгс). Единица массы является производной от этих единиц. Масса выражается в технических единицах массы (т. е. м.). Одну техническую единицу массы имеет тело, которое под действием силы в 1 кгс получает ускорение в 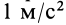. Из (2) получаем, что массу в 1 т. е. м. имеет тело, сила тяжести которого равна 9,8 кгс.