Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

Напомним что:

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения - не равносильны, так как корнем первого уравнения является число 10, а корнем второго - число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Рассмотрим уравнения:

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения - дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и - целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, - единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Ответ. 3.

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

х - 1 х - 2

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Ответ. 4.

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 - единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

1) найти ОДЗ переменной в уравнении; & 2) найти простейший общий знаменатель дробей, входящий в уравнение;

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе - два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Ответ. Нет.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где - натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями - это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Пример №206

Замените степень дробью:

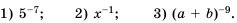
Решение:

По определению:

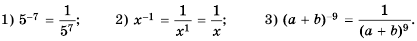
Пример №207

Замените дробь степенью с целым отрицательным показателем:

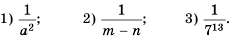
Решение:

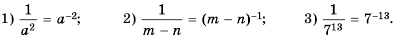
Пример №208

Вычислите: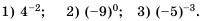

Решение:

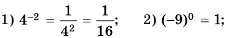
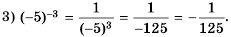
Рассмотрим, как возвести дробь 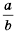в целую отрицательную степень. Если 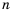- натуральное число и 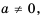имеем:

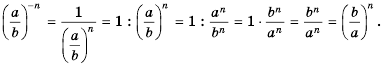
Следовательно,

Если 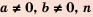- натуральное число, то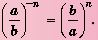

Пример №209

Найдите значение выражения:

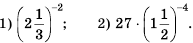
Решение:

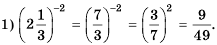
2) Учитывая порядок выполнения арифметических действий, сначала возведем дробь в степень, а затем выполним умножение:

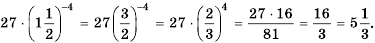
Ответ.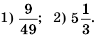

Свойства степени с целым показателем

Свойства степени с натуральным показателем справедливы и для степени с ненулевым основанием и целым показателем. Следовательно,

Для любого 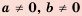любых целых

Эти свойства можно доказать на основании формулы 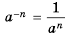и свойств степени с натуральным показателем.

Докажем, например, формулу 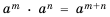для случая, когда 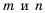отрицательные целые числа.

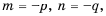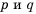Пусть где натуральные числа. Имеем:

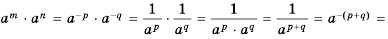
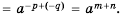
Следовательно, 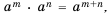где 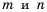- отрицательные целые числа. В случае, когда один из показателе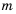й или 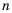-целое отрицательное число, а второй - натуральное число или нуль, формула доказывается аналогично.

Пример №210

Выполните действие:

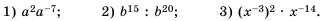
Решение:

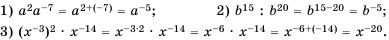
Пример №211

Упростите выражение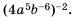

Решение:

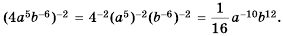
Пример №212

Вычислите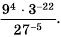

Решение:

Представим 9 и 27 в виде степени с основанием 3 и воспользуемся свойствами степени:

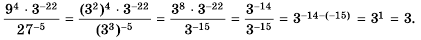
Ответ. 3.

Стандартный вид числа

В физике, химии, технике, астрономии часто имеют дело как с очень большими, так и с очень малыми значениями величин. Например, масса Земли равна 5 976 ООО ООО ООО ООО ООО ООО ООО кг, а диаметр молекулы водорода 0,00000000025 м.

Читать или записывать такие числа в виде десятичных дробей неудобно, неудобно и использовать десятичную их запись при вычислениях. В таких случаях имеет смысл записывать число в ви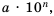де где 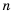- целое число,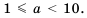

Например,

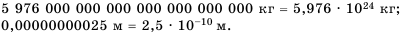
Говорят, что числа 5 976 000 000 000 000 000 000 000 и 0,00000000025 записаны в стандартном виде.

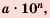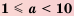Стандартным видом числа называют его запись в виде произведении где и 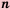— целое число.

Если число записано в стандартном виде, то показатель степени 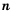называют порядком числа. Например, порядок числа, которым записана масса Земли в килограммах, равен 24, а порядок числа, которым записан диаметр молекулы водорода в метрах, равен -10.

В стандартном виде можно записать любое положительное число. Порядок числа дает представление об этом числе.

Если порядок числа 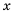равен 4, это значит, что 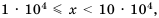то есть 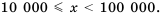Если порядок числа 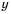равен -2, то 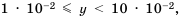то есть 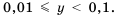Большой положительный порядок числа показывает, что число очень большое. Большой по модулю отрицательный порядок числа показывает, что число очень маленькое.

Следовательно, если говорят, что одно число на порядок больше второго, это означает, что оно в 10 раз больше второго, если на два порядка - в 100 раз больше и т. д.

Пример №213

Представьте число 272 000 в стандартном виде.

Решение:

В данном числе поставим занятую так, чтобы в целой части была одна цифра, отличная от нуля. В итоге будем иметь 2,72. Занятой отделили 5 цифр с конца числа, чем уменьшили данное число в 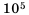раз. Следовательно,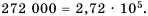

Ответ.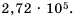

Пример №214

Представьте число 0,00013 в стандартном виде.

Решение:

В данном числе перенесем запятую на 4 знака вправо, будем иметь 1,3. При этом число увеличили в 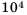раз (на 4 порядка). Следовательно,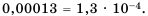

Ответ.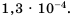

Пример №215

Выполните действия и представьте результат в стандартном виде:

Решение:

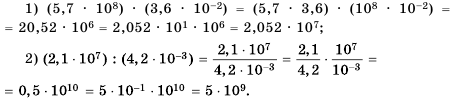
Ответ.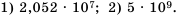

Пример №216

Найдите сумму 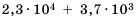и запишите результат в стандартном виде.

Решение:

Имеем два слагаемых разных порядков.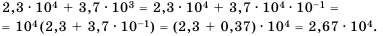

Ответ.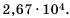

Функция Y=K/X ее график и свойства

Функция 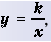ее график и свойства

Пример №217

Пешеход должен преодолеть путь в 16 км. Если он будет двигаться со скоростью 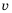км/ч, то зависимость времени 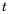(в часах) для преодоления этого расстояния от скорости движения можно выразить формулой 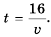При увеличении значения 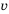в несколько раз значение 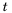во столько же раз уменьшится. В этом случае говорят, что переменные 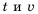обратно пропорциональны.

Пример №218

Площадь прямоугольника равна 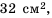а одна из его сторон 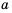см. Тогда вторую сторону 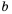(в см) можно найти по формуле 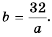Здесь переменные 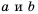также обратно пропорциональны.

В примерах 1 и 2 переменные 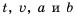принимают только положительные значения. В дальнейшем будем рассматривать функции, которые задают формулой вида 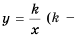число, 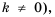где переменные 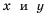могут принимать как положительные, так и отрицательные значения. Каждую из таких функций называют обратной пропорциональностью.

Функцию вида 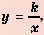где 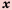— независимая неременная, 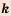- некоторое отличное от нуля число, называют обратной пропорциональностью.

Область определения функции 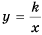все числа за исключением нуля, так как при 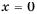выражение не имеет смысла.

Построим график функции 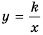отдельно для каждого из случаев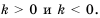

Пример №219

Постройте график функции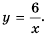

Решение:

Составим таблицу значений функции 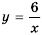для нескольких значений аргумента:

Отметим на координатной плоскости точки из составленной таблицы (рис. 2).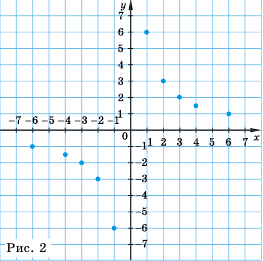

Если бы мы на этой плоскости обозначили больше точек, удовлетворяющих формуле 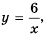а потом соединили их плавной линией, то получили бы график функции 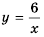(рис. 3).

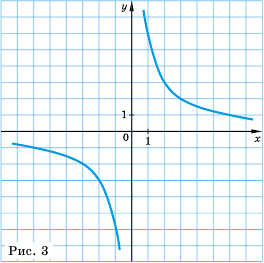
График обратной пропорциональности называют гиперболой.

Гипербола состоит из двух ветвей. Для функции 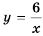одна из них лежит в первой координатной четверти, а другая - в третьей. Гипербола не пересекает координатные оси: график не содержит точек, у которых 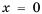(т. к. нуль не принадлежит области определения функции), и не содержит точек, у которых

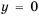(т. к. уравнение 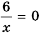не имеет решений). Чем больше по модулю значение 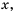тем меньше по модулю значение 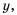и наоборот, чем меньше по модулю значение 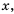тем больше по модулю значение 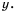Это значит, что ветви гиперболы неограниченно приближаются к осям координат.

Так же выглядит график функции 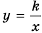при любом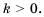

Пример №220

Постройте график функции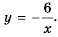

Решение:

Рассуждая как и в предыдущем примере, построим график функции 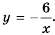Он изображен на рисунке 4.

Это также гипербола, одна из ветвей которой лежит во второй координатной четверти, а другая - в четвертой.

Так же выглядит график функции 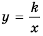при любом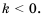

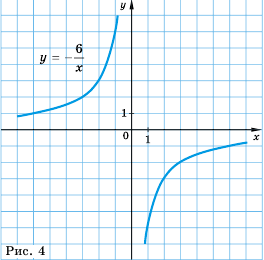
Обобщим свойства обратной пропорциональности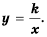

1. Область определения функции состоит из всех чисел за исключением нуля.

2. Область значений функции состоит из всех чисел за исключением нуля.

3. График функции - гипербола, ветви которой при лежат в первой и третьей координатных четвертях, а при - во второй и четвертой.

4. Ветви гиперболы неограниченно приближаются к осям координат.

Пример №221

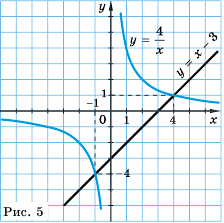
Постройте в одной системе координат графики функций 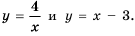Найдите их точки пересечения и, пользуясь построенным графиком, решите уравнение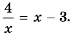

Решение:

График функции 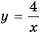гипербола, ветви которой лежат в первой и третьей координатных четвертях, а график функции 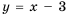прямая, проходящая через точки 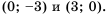Графики функций изображены на рисунке 5. Они пересекаются в точках 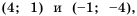абсциссы 4 и -1 которых являются решениями уравнения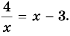

Действительно, при 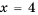выражения 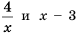принимают

равные значения: 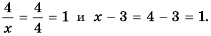При 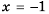аналогично: 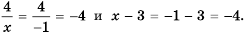Следовательно, числа 4 и -1 - корни уравнения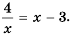

Ответ: 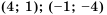- точки пересечения; 4, -1 - корни уравнения.

Предложенный в примере 5 метод решения уравнений называют графическим методом решения уравнений.

Если абсцисса точки пересечения графиков функций - целое число, надо выполнить проверку, т. к. часто корни уравнения этим методом можно найти только приблизительно.

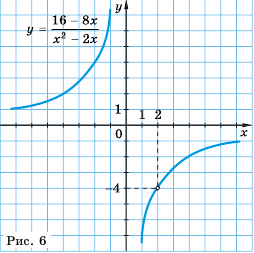
Пример №222

Постройте график функции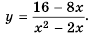

Решение:

Область определения функции - все числа за исключением чисел 0 и 2, которые обращают знаменатель в нуль.

Упростим дробь: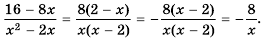

Значит при условии 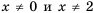функция принимает вид 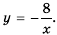Графиком функции 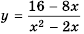является гипербола 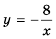с «выколотой» точкой 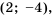точек же с абсциссой 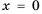у гиперболы нет (рис. 6).

------------

Если все решения одного уравнения также являются решениями второго, то второе уравнение называется следствием первого уравнения.

Если множества решений двух уравнений совпадают, то эти уравнения называются равносильными.

Пример 1.

Равносильны ли уравнения?

Решение:

1) Оба уравнения имеют общий корень: х=1. Так как они не имеют других корней, то они являются равносильными.

2) Первое уравнение имеет корень, равный 0. Второе же уравнение такого корня не имеет. Значит, данные уравнения не равносильны.

Пусть Р(х) и Q(x) - многочлены переменной х.

Выражение вида 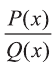называется рациональным.

Пусть А(х) и В(х) - рациональные выражения. Уравнение вида А(х)=В(х) называется рациональным.

Рассмотрим сначала простейшее рациональное уравнение вида

Известно, что дробь 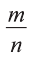равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля (на нуль делить нельзя!). Значит, для того, чтобы решить уравнение (1) , необходимо и достаточно найти все значения неизвестной х, для которых одновременно выполнены условия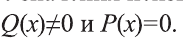

Для краткости, это мы будем записывать так: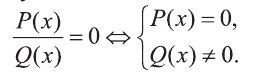

• Заказать решение задач по высшей математике

Пример:

Решите уравнение:

Решение:

Уравнение 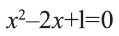имеет единственное решение х=1. При х=1 знаменатель отличен от нуля. Значит, данное уравнение тоже имеет единственное решение х=1.

2) Квадратное уравнение 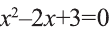не имеет корней, так как 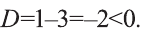Значит, данное уравнение тоже не имеет корней.

3) Для квадратного уравнения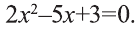

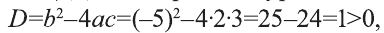Значит, это уравнение имеет два корня:

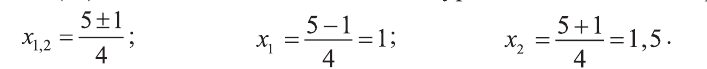
Однако число 1,5 обращает знаменатель выражения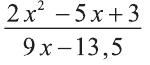

в нуль, а число 1 - нет. Значит, данное уравнение имеет единственное решение х=1.

4) Уравнение 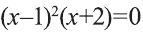имеет два корня 1 и-2. Однако число 1 обращает знаменатель (х-1) в нуль, а число -2 - нет. Значит, данное уравнение имеет единственное решение х=—2.

В случае, когда хотя бы одно из выражений А(х) и В(х) представимо в виде суммы нескольких рациональных выражений, рациональное уравнение А(х)=В(х) можно решить так:

• 1 шаг. Ищем общий знаменатель дробей, входящих в уравнение;
• 2 шаг. Обе части уравнения умножаем на этот общий знаменатель;
• 3 шаг. Ищем решения полученного уравнения;
• 4 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель в нуль.

Пример:

Решите уравнение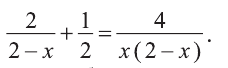

Решение:

Умножаем обе части уравнения на общий знаменатель 2х(2-х). Упрощая полученное уравнение 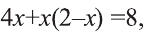, приводим его к следующему квадратному уравнению: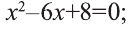

Так как D=9-8=l>0, то данное квадратное уравнение имеет два корня:

х=2; х=4.

Проверка.

При х=2 знаменатель обращается в нуль: х(2-х) = 2(2-2) = 0. Значит, х=2

не является решением исходного уравнения.

При х=4 знаменатель отличен от нуля х(2-х) = 4(2-4) Ф 0. Значит, х=4

является решением исходного уравнения.

Если 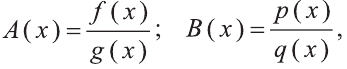то при решении рационального уравнения вида 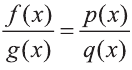полезно воспользоваться основным свойством пропорции: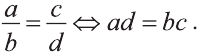

При этом получим следующий алгоритм решения:

• 1 шаг. Ищем решения уравнения f (х)q(х) = р(х)g(х)
• 2 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель q(x)g(x) в нуль.

Пример:

Решите уравнение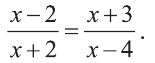

Решение:

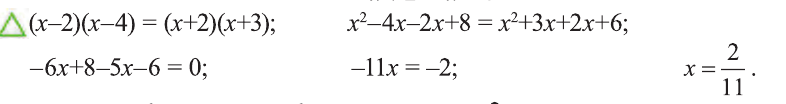
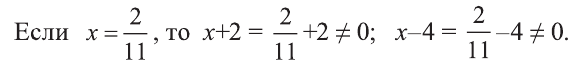
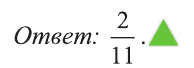
В некоторых случаях удачно выполненная замена позволяет привести заданное уравнение к более простому.

Пример:

Решите уравнение:

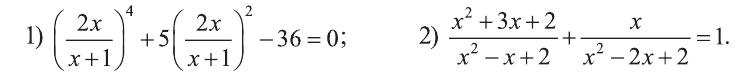
Решение:

 1) Выполним замену 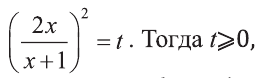а уравнение получит вид 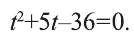Последнее имеет корни t=-9 и t=4, из которых второе положительно.

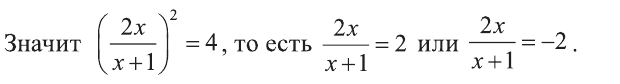
При 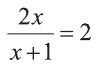уравнение не имеет решение, а при 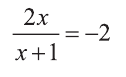уравнение имеет единственное решение х=-0,5.

Ответ: х=-0,5. 

2) Очевидно, что х=0 удовлетворяет уравнению. Пусть 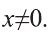. Разделив в каждой дроби уравнения числитель и знаменатель на х, получим уравнение

Тогда наше уравнение получит вид: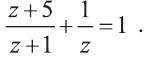

Решим последнее уравнение:

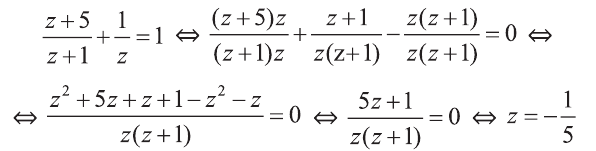
Теперь найдем x.

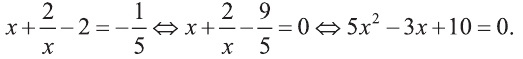
В силу того, что дискриминант квадратного уравнения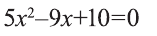 отрицателен, то последнее уравнение не имеет действительных решений. Ответ: х=0.

Системы рациональных уравнений

Решение систем, состоящих из рациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует не забывать, что знаменатели, участвующих рациональных выражений, не могут обращаться в нуль.

Пример:

Решите систему:

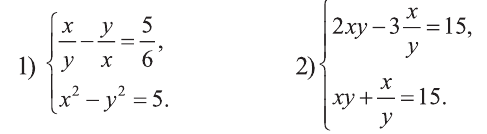
Решение:

1) Сделаем в первом уравнении замену 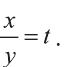Получим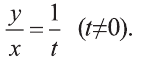

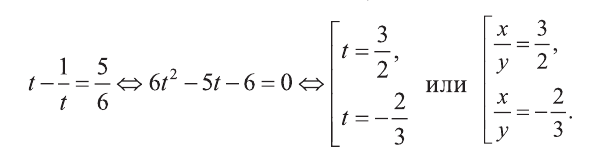
Отсюда или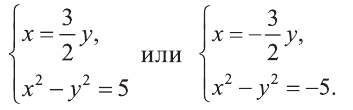

Решим полученные системы: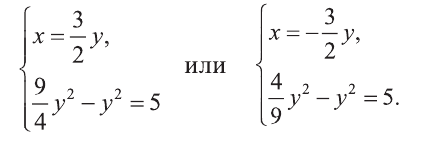

Первая система имеет решения (3,2), (-3, -2), а вторая не имеет решений. Ответ: (3; 2), (-3; -2).

2). Обозначим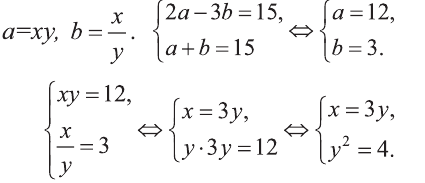

------

Рациональные уравнения

Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.

Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.

Это интересно!

На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.

Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.

Рациональные уравнения

Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).

Пример:

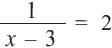В данном уравнении ОДЗ 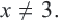Учитывая, что 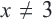умножим обе части уравнения на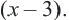

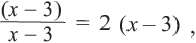отсюда получим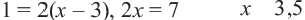

Подставим полученное значение в уравнение: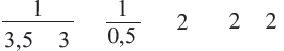

Таким образом, 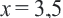является корнем уравнения. Данное уравнение не имеет других корней.

Пример:

Решим уравнение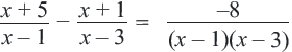

ОДЗ данного уравнения 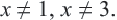Умножим обе части уравнения на общий

знаменатель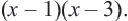

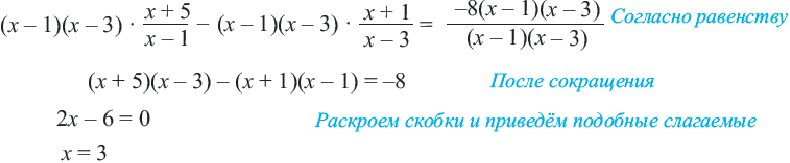
Пример:

В уравнении, 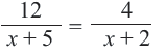ОДЗ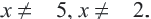

Используя свойство пропорции можно написать: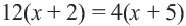

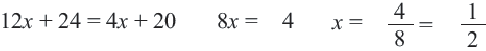
Пример:

Решим уравнение. 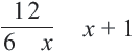Здесь ОДЗ,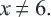

Умножим обе части уравнения на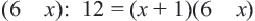

Отсюда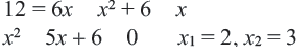

Проверьте, являются ли оба этих числа корнями данного уравнения.

Пример:

Решим уравнение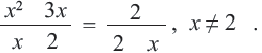

Запишем уравнение в виде 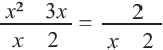и умножим обе стороны на общий множитель 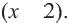Получим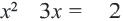

Отсюда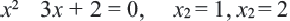

При проверке, убеждаемся что, 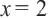не удовлетворяет уравнению, т.к. превращает знаменатель в «0». Таким образом, корнем данного уравнения является только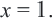

Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней.

Решение задач с помощью рациональных уравнений

Задачи на работу

Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за 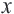дней, тогда 1-ый рабочий выполнит её за 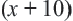дней

Первый рабочий за 1 день выполняет 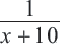- ую часть работы, 2-ой - 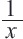- ую. Вместе, за 1 день они выполнят 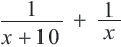часть работы. Зная, что вместе за 1 день они выполняют 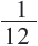часть работы (согласно условию), составим уравнение 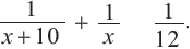Умножим обе части уравнения на 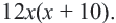Получим, 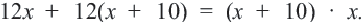После упрощения имеем Решением данного уравнения являются числа и 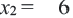(не удовлетворяет условию, т.к. ). Итак 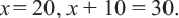Ответ: 2-ой рабочий выполняет работу за 20 дней, а 1-ый - за 30 дней.

Задачи на движение

Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.

1-й способ:

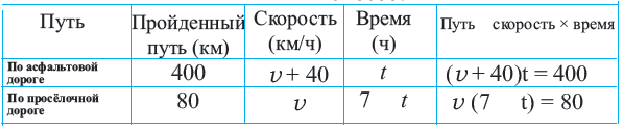Из 2-ой строки таблицы: 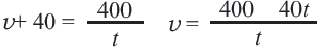Из 3-е1 строки таблицы: 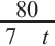Отсюда получаем рациональное уравнение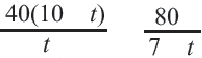

Разделим обе части уравнения на 40: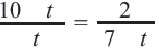

Получим 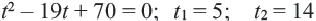(противоречит условию задачи)

Ответ: по просёлочной дороге 2 часа

2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом 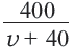часов, а по проселочной дороге 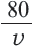часов.

Зная, что на весь путь он потратил 7 часов, составим уравнение: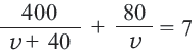

Решив данное уравнение, получим 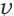= 40 км/ч. Тогда по просёлочной дороге он двигался 80 : 40 = 2 часа.