
Проекция вектора на ось в физике - формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка 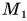
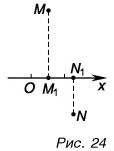
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 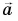 на ось Ох обозначена через
на ось Ох обозначена через 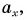 а проекция вектора
а проекция вектора 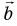 — через
— через 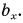
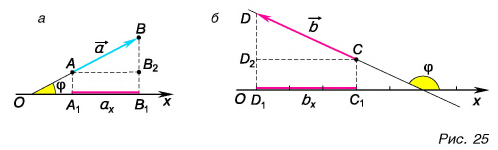
Проекция 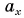 — число положительное, т. к. угол
— число положительное, т. к. угол 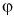 на рисунке 25, а — острый. Проекция
на рисунке 25, а — острый. Проекция 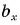 — число отрицательное
— число отрицательное 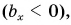 т. к. угол
т. к. угол 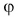 на рисунке 25, б — тупой.
на рисунке 25, б — тупой.
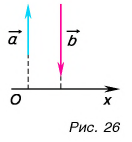
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 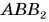 на рисунке 25, а. Его гипотенуза
на рисунке 25, а. Его гипотенуза 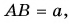 катет
катет 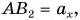 а угол между ними равен
а угол между ними равен 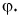 Следовательно,
Следовательно,

Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
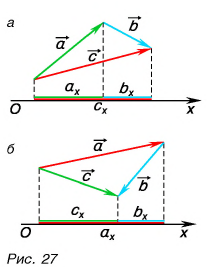
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 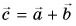 следует равенство для проекций:
следует равенство для проекций: 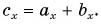 Не забывайте о знаках проекций.
Не забывайте о знаках проекций.
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
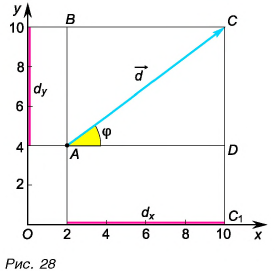
Рассмотрим вектор 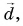 лежащий в плоскости
лежащий в плоскости 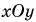 (рис. 28). Его проекции на оси
(рис. 28). Его проекции на оси 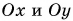 определим из рисунка:
определим из рисунка: 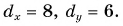
Модуль вектора 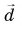 находим по теореме Пифагора из треугольника ACD:
находим по теореме Пифагора из треугольника ACD: 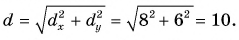 Разделив
Разделив 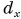 на
на 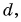 получим:
получим: 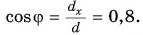 По значению косинуса находим угол
По значению косинуса находим угол 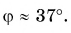
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
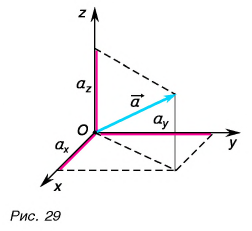
Вектор в пространстве определяется тремя проекциями: 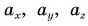 (рис. 29).
(рис. 29).
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
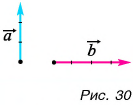
1. Определите сумму и разность взаимно перпендикулярных векторов  (рис. 30). Найдите модули векторов суммы
(рис. 30). Найдите модули векторов суммы  и разности
и разности 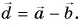
Решение
Сумму векторов 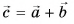 находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы
находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы 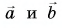 взаимно перпендикулярны, модуль вектора
взаимно перпендикулярны, модуль вектора 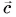 находим по теореме Пифагора:
находим по теореме Пифагора: 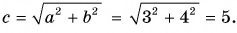 Разность векторов
Разность векторов 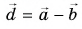 определим по правилам вычитания векторов (рис. 32, а, б).
определим по правилам вычитания векторов (рис. 32, а, б).

Модуль вектора 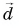 находим аналогично:
находим аналогично:
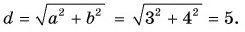
Ответ: 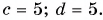
Пример №2
Выразите вектор 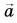 через векторы
через векторы 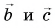 (рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
(рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
Решение
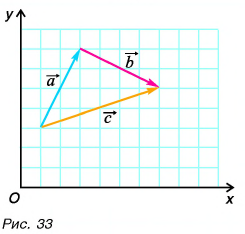
По правилу треугольника находим: 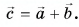 Отсюда
Отсюда 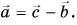 Определив координаты
Определив координаты  начальных и конечных точек векторов
начальных и конечных точек векторов 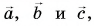 находим проекции этих векторов:
находим проекции этих векторов: 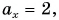

Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы: 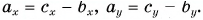
Ответ: 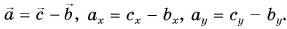
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |