Чертежи точки, отрезка прямой в начертательной геометрии с примерами

Содержание:

Чертежи точки, отрезка прямой:

Эпюр Монжа, построенный по схеме рассмотренной выше, позволяет однозначно судить как о форме и положении объектов в пространстве, так и о расположении их по отношению к плоскостям проекции.

Комплексные чертежи точки

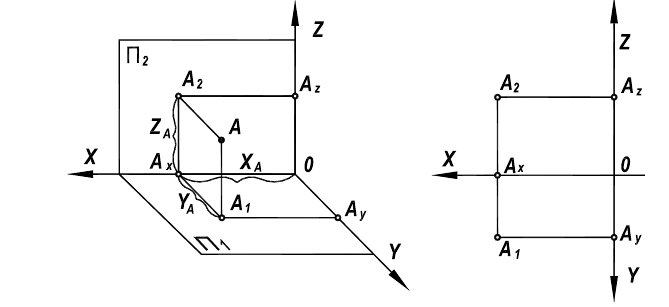
Рисунок 2.1 - Чертеж точки в пространстве

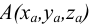
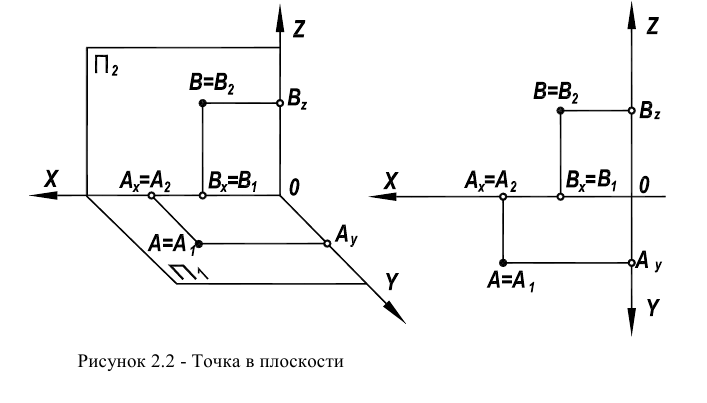
На этом чертеже присутствуют две ее проекции: горизонтальная - 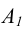и, соответствующая ей, фронтальная - 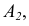объединенные линией связи 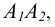ортогональной оси чертежа Ох.

Чертеж точек, лежащих в плоскостях проекций, представлен на рисунке 2.2. Точка 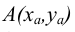лежит в горизонтальной плоскости проекции 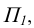а вторая точка 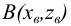- во фронтальной плоскости проекции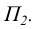

Отличием этого чертежа от предыдущего является то, что одна из проекций этих точек оказывается на оси чертежа Ох.

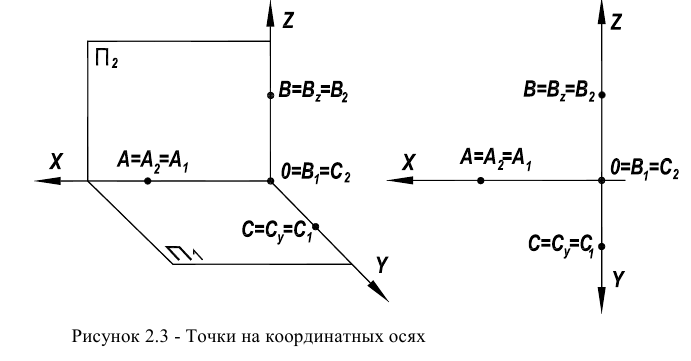
Точки, лежащие на координатных осях, изображены на рисунке 2.3. Точка 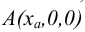лежит на оси Ох, точка 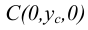- на оси Оу, а точка 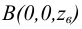-на оси Oz. Для чертежей этих точек характерно следующее.

Обе проекции точки А, лежащей на оси чертежа , совпадают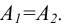

У точки С, лежащей на оси Оу, фронтальная проекция совпадает с точкой начала координат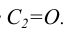
Аналогичная ситуация и с точкой В, лежащей на оси Oz, ее горизонтальная проекция совпадает с точкой начала координат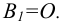

Комплексные чертежи прямых

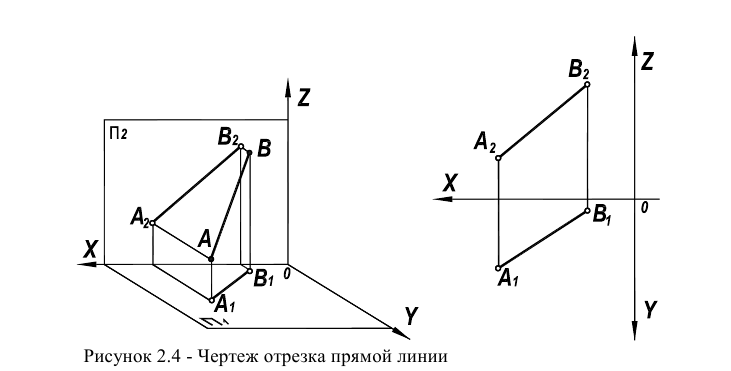
Будем прямую на чертеже задавать ее симплексом (отрезком). Для этого достаточно на чертеже задать две произвольные точки (в случае их совпадения длина отрезка будет нулевой). Чертеж отрезка прямой АВ приведен на рисунке 2.4.

Все прямые могут быть классифицированы в зависимости от их расположения по отношению к плоскостям проекций.

Прямая, не параллельная ни одной плоскости проекции, получила название прямой общего положения. Чертеж такой прямой приведен выше на рисунке 2.4.

Характерной особенностью чертежа такой прямой является непараллельность ее проекций ни одной из координатных осей.

Прямые, параллельные плоскостям проекций, получили название линий уровня.

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной линией уровня.

Фронтальная проекция 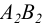такой прямой параллельна оси чертежа, а горизонтальная проекция 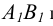проецируется в отрезок, равный по длине самому отрезку АВ (рисунок 2.5).

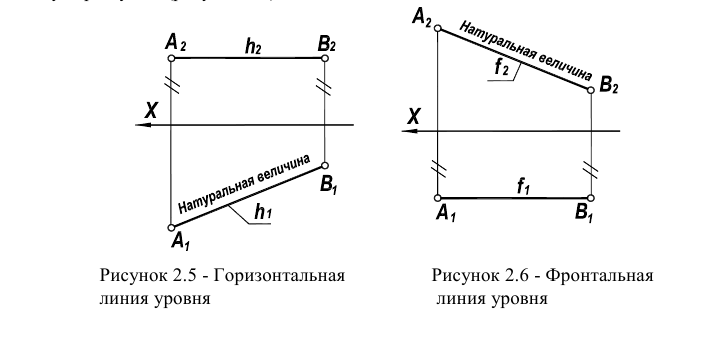
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной линией уровня.

Горизонтальная проекция 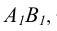такой прямой параллельна оси чертежа, а фронтальная проекция 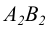проецируется в отрезок, равный по длине отрезку АВ (рисунок 2.6).

Характерным для чертежей линий уровня является то, что одна из их проекций параллельна оси чертежа.

Линии, перпендикулярные плоскостям проекций, получили название проецирующих прямых.

Прямая, перпендикулярная фронтальной плоскости проекции 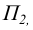называется фронтально - проецирующей прямой. Такая прямая параллельная координатной оси Оу. На чертеже такой прямой (рисунок 2.8) фронтальная проекция 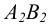вырождается в точку, а горизонтальная проекция 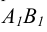перпендикулярна оси чертежа (совпадает по направлению с линиями связи).

Прямая, перпендикулярная горизонтальной плоскости проекции 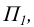называется горизонтально - проецирующей прямой. Такая прямая параллельна координатной оси Oz.

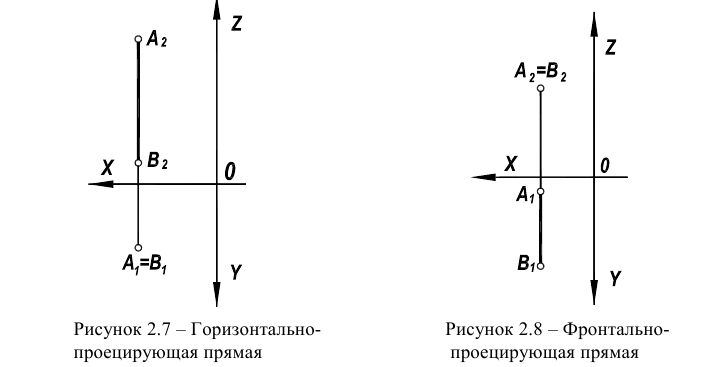
На чертеже прямой (рисунок 2.7) горизонтальная проекция 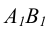вырождается в точку, а фронтальная 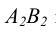перпендикулярна оси чертежа (совпадает по направлению с линиями связи).

Характерной особенностью чертежей проецирующих прямых является то, что одна из проекций у них вырожденная, а вторая - параллельна одной из координатных осей (рисунок 2.7, 2.8).

Линии уровня и проецирующие прямые объединяют в одну группу - линий частного положения.

• Заказать чертежи

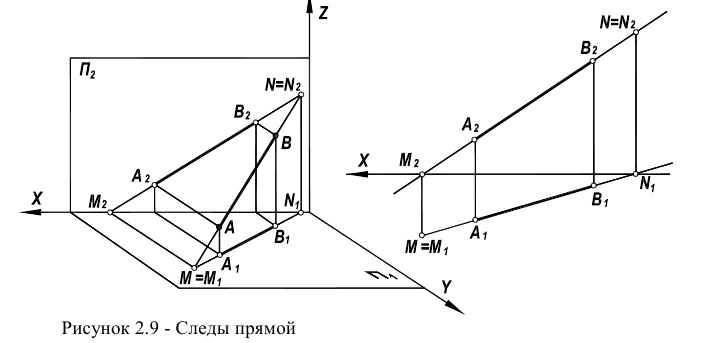
Следы прямой

Очевидно, что прямая и плоскость пересекаются в точке. Точки пересечения прямой с плоскостями проекции получили название следов прямой. Точка пересечения прямой с фронтальной плоскостью проекций 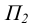называется фронтальным следом, а с горизонтальной плоскостью проекций 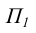- горизонтальным следом.

Следы прямой, заданной на чертеже отрезком AВ, можно найти исходя из определения данного выше.

След - это одна из точек прямой, лежащая в плоскости проекции. Следовательно, одна из координат этой точки должна быть равна нулю (в соответствии с рисунком 2.1).

При определении положения фронтального следа N прямой необходимо продлить горизонтальную проекцию 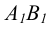до пересечения с осью чертежа (рисунок 2.9). Эта точка пересечения 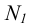может быть принята за горизонтальную проекцию искомого следа. Фронтальная проекция 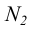следа найдется по соответствию на фронтальной проекции прямой 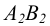(см. рисунок 2.9). Очевидно, что точка N лежит на прямой АВ (ее проекции лежат на соответствующих проекциях этой прямой).

Вместе с этим у нее координата Y равна нулю (горизонтальная проекция 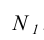лежит на оси чертежа). Следовательно, можно утверждать, что точка N- это фронтальный след прямой.

Аналогично может быть построен и горизонтальный след М. Для этого

следует продлить фронтальную проекцию отрезка А 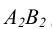до пересечения с осью чертежа и принять точку пересечения за фронтальную проекцию искомого следа 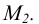Горизонтальная проекция следа 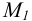найдется по соответствию на горизонтальной проекции прямой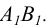

Взаимное расположение прямых

Прямые могут быть классифицированы и по такому признаку, как взаимное расположение в пространстве

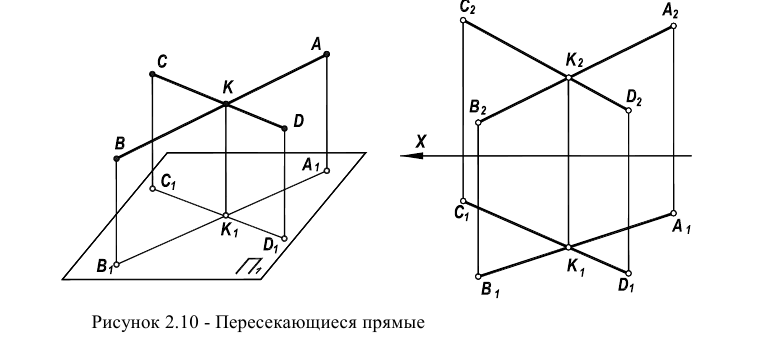
Рассмотрим вариант пересекающихся прямых, лежащих в произвольной плоскости. По определению две прямые пересекаются, если имеют одну общую точку.

На рисунке 2.10 изображен чертеж пересекающихся прямых АВ и CD. Точка пересечения К одновременно принадлежит двум этим прямым.

Это является следствием того, что на комплексном чертеже соответствующие проекции этой точки одновременно принадлежат соответствующим проекциям прямых (фронтальные проекции - фронтальным, а горизонтальные -горизонтальным).

Частным случаем пересечения прямых являются параллельность. Параллельные прямые пересекаются в несобственной точке.

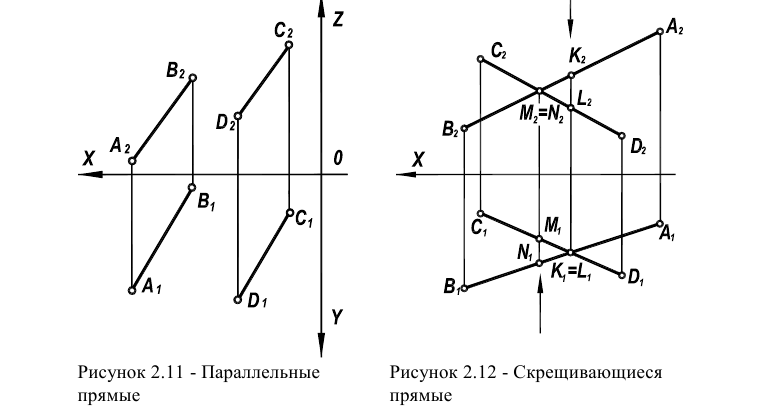
Характерной особенностью чертежа параллельных прямых является параллельность одноименных проекций. В соответствие с рисунком 2.11

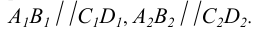
Прямые в пространстве, не имеющие общих точек, называются скрещивающимися (рисунок 2.12).

Точки пересечения их горизонтальных 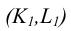и фронтальных 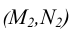являются совпадающими проекциями различных точек. Такие точки, принадлежащие разным прямым, называют конкурирующими.

Конкурирующие точки используются для анализа видимости и глубины сцены в системах машинной графики.